توابع مثلثاتی
| مثلثات |
|---|
 |
| منابع |
| قوانین و قضایا |
| حساب دیفرانسیل و انتگرال |
در ریاضیات، منظور از توابع مثلثاتی شش تابع سینوس، کسینوس، تانژانت، کتانژانت، سکانت و کسکانت است که این توابع رابطهٔ میان زاویهها و ضلعهای یک مثلث قائمالزاویه را نشان میدهند و به همین دلیل توابع مثلثاتی نامیده میشوند. قدمت اولین متنهای بهجامانده از توابع مثلثاتی به دوران پیش از میلاد در مصر و یونان بازمیگردد. قضیهٔ تالس توسط تالس در سدهٔ ششم پیش از میلاد در مصر مطرح شد، همچنین از قضیهٔ فیثاغورس به عنوان سنگ بنای مثلثات یاد میشود. علاوه بر مصر و یونان، کشورهای دیگری از جمله چین، هند، کشورهای اسلامی و کشورهای اروپایی پیشبردهای مطرحی در زمینهٔ مثلثات داشتند که میتوان به افرادی چون خوارزمی، بتانی، ابوالوفا محمد بوزجانی، شن کو، گو شوجینگ و رتیکوس اشاره کرد.
تعاریف متفاوتی از توابع مثلثاتی بیان شدهاست، سادهترین آنها بر پایهٔ دایرهٔ واحد است که در این تعریف دایرهای با شعاع ۱ ترسیم میشود و شعاعی با زاویهٔ مشخص نسبت به محور افقی روی آن رسم شده و یک مثلث را تشکیل میدهد. هر یک از توابع مثلثاتی را میتوان با پارهخطی در این دایره نشان داد. تعاریف دیگری از توابع مثلثاتی نیز بر پایهٔ انتگرال، سری توانی و معادلهٔ دیفرانسیل بیان شدهاست که هر یک از آنها کاربرد خاص خود را دارند. برای نمونه در تعریف بر پایهٔ سری توانی، از سری مکلورن استفاده میشود که در محاسبهٔ مقدار تقریبی آنها توابع مثلثاتی استفاده فراوان دارد.
توابع مثلثاتی بر روی یک زاویه عملیات انجام میدهند و یک عدد حقیقی را برمیگردانند و هر یک از آنها ویژگیهای خاص خود را دارند، از جمله زوج یا فرد بودن، متناوب بودن، پیوسته بودن، متعامد بودن. کاربرد اصلی این تابعها در محاسبهٔ اندازهٔ ضلعها و زاویههای یک مثلث و سایر عوامل مرتبط با آنها است. این کاربرد، در دانشهای مختلفی مانند نقشهبرداری، ناوبری و زمینههای گوناگون فیزیک مورد استفاده قرار میگیرد. در نقشهبرداری، با استفاده از اندازهگیری زاویهٔ یک نقطه نسبت به دو نقطه معین، مختصات آن نقطه را محاسبه میکنند که امروزه از این روش برای اندازهگیری سهبعدی نوری استفاده میشود یا در ناوبری، تنظیم خط سیر کشتیها و سایر شناورها بر پایهٔ اجسام ثابت مانند فانوس دریایی با بهرهگیری از توابع مثلثاتی انجام میشود. همچنین به علت خاصیت تناوبی بودن این تابعها، از آنها در مدلسازی فرایندهای نوسانی مانند نور و موج استفاده میشود. برای نمونه قانون اسنل بنیادیترین کاربرد توابع مثلثاتی است که در پدیدهٔ شکست نور به کار میرود. از دیگر کاربردهای توابع مثلثاتی میتوان به استفاده آن در صنعت برق و مخابرات اشاره کرد. از جمله کاربرد امواج سینوسی در جریانهای متناوب و همچنین انواع مدولاسیون که برپایه همین امواج سینوسی انجام میشود.
تاریخچه[ویرایش]

شواهد بهکارگیری توابع مثلثاتی در زمینههای گوناگون، به ویژه در نجوم، در بسیاری از متون به جا مانده از دوران پیش از میلاد از جمله در یونان و مصر وجود دارد. یکی از کهنترین مطالب مرتبط با مثلثات که در متون تاریخی بیان شده، قضیه تالس است. تالس که در سده ششم پیش از میلاد در مصر تحصیل میکرد، برای حل مسئلهٔ محاسبهٔ ارتفاع هرم خئوپس، روشی تازه را ارائه نمود که بعداً با عنوان قضیه تالس شناخته شد. میتوان قضیهٔ فیثاغورس را سنگ بنای مثلثات دانست.[۱] در بسیاری از متون یونان باستان، کاربردهای مثلثات مورد توجه قرار گرفتهاند. ابرخس، نخستین جدول مثلثاتی را ایجاد نمود و به همین دلیل، او را پدر مثلثات مینامند. منلائوس مثلثات کروی را پایهگذاری کرد.[۲] بطلمیوس در المجسطی، رابطهٔ سینوس و کسینوس مجموع و تفاضل دو زاویه را بیان کرد.[۳]
مطالعه در زمینهٔ توابع مثلثاتی در هند نیز رواج داشتهاست. از جمله، در کتاب سوریا سیدهانتا در سدهٔ چهارم میلادی از جدول سینوس به جای جدول وتری در نجوم استفاده شدهاست.[۴] همچنین به نظر میرسد که نامهای سینوس و کسینوس، تغییر یافتهٔ توابع جیا و کوتیجیا در نجوم دوره گوپتای هند باشند. مدهاوه در سدهٔ چهاردهم سری تیلور تابعهای سینوس، کسینوس و تانژانت را به دست آورد.[۲]
دوران طلایی اسلام، تأثیر قابل توجهی بر پیشرفت علوم ریاضی و از جملهٔ آنها مثلثات داشت. خوارزمی، جدولهای نجومی و مثلثاتی (مربوط به سینوس و تانژانت) را تهیه کرد.[۵] مروزی جدول کتانژانت را تهیه کرد. در آثار بتانی در سدهٔ سوم شمسی (سدهٔ نهم میلادی)، مثلثات بهطور وسیعی به کار رفتهاست که از جمله میتوان به جدول کسکانت اشاره کرد. ابوالوفا محمد بوزجانی در سدهٔ چهارم شمسی (سدهٔ دهم میلادی)، قانون سینوسها را به دست آورد.[۶] ابوریحان بیرونی مثلثسازی را برای تهیهٔ نقشه به کار گرفت. در پایان سدهٔ یازدهم، عمر خیام معادلات درجهٔ سوم را با حل عددی تقریبی که از درونیابی جداول مثلثاتی به دست میآمد، حل کرد. همچنین غیاثالدین جمشید کاشانی در سدهٔ پانزدهم میلادی، سینوس زاویهٔ ۱ درجه را با حل معادلهٔ درجهٔ ۳ برحسب زاویهٔ ۳ درجه تا ۱۷ رقم اعشار محاسبه کرد.[۷]
دانشمندان چینی چندان به مطالعهٔ مثلثات نمیپرداختند. دو ریاضیدان چینی با نام شن کو و گو شوجینگ مطالعاتی را در زمینه توابع مثلثاتی انجام دادند. برای نمونه، شن کو یک رابطهٔ تقریبی برای محاسبهٔ طول کمان برحسب قطر دایره، زه و طول وتر به دست آورد.[۸]
احتمالاً رتیکوس نخستین شخص اروپایی بود که در سدهٔ شانزدهم میلادی، توابع مثلثاتی را به جای دایره برحسب زاویهٔ قائمه تعریف کرد و جدولهای هر شش تابع را تهیه نمود. مقالهٔ اویلر در ۱۷۴۸ میلادی به عنوان پایهگذار اصلی رفتار تحلیلی با توابع مثلثاتی در اروپا دانسته میشود. اویلر توابع مثلثاتی را به صورت سری نامتناهی تعریف کرد و فرمول اویلر را ارائه نمود.[۲]
نامگذاری[ویرایش]
در متون سانسکریت، از نامهای جیوا (به معنی وتر) و کوجیوا برای نامگذاری دو تابع اصلی مثلثاتی (سینوس و کسینوس) استفاده میشد. در برگرداندن به زبان عربی، جیوا به جیب تبدیل شد[۲] که البته در فارسی هم مورد استفاده قرار گرفت.[۹] دانشمندان مسلمان، سایر توابع مثلثاتی را نیز میشناختند و آنها را نامگذاری کردهبودند. جدول زیر، نامهای به کار رفته برای توابع مثلثاتی در متون دانشمندان مسلمان را نشان میدهد:[۱۰]
| نام قدیم در فارسی | معنی نام | نام امروزی |
|---|---|---|
| جَیْب | گریبان | سینوس |
| جَیْبِ تمام | گریبان پُر | کُسینوس |
| ظِلّ، ظِلِّ معکوس | سایه | تانژانت |
| ظِلِّ تمام، ظِلِّ مُسْتَوی | سایهٔ پُر | کُتانژانت |
| قاطع، قطر ظِلّ | بُرنده | سِکانت |
| قاطع تمام | بُرندهٔ پُر | کُسکانت |
دانشمندان اروپایی که متنهای عربی را به لاتین ترجمه میکردند، جیب را به صورت جَیب میخواندند (که به معنی خلیج است). بنابراین آن را به سینوس (که واژهای لاتینی به معنی خلیج است) برگرداندند.[۲]
تعریف بر پایهٔ مثلث قائمالزاویه[ویرایش]
شکل روبرو، یک مثلث قائمالزاویه را نشان میدهد که از سه ضلع a و b و c و زاویههای A و B و C تشکیل شدهاست. زاویهٔ C برابر ۹۰ درجه است و دو زاویهٔ دیگر، زاویهٔ تند و متمم هستند، به عبارت دیگر، مجموع دو زاویه برابر ۹۰ درجه است. ضلع روبرو به زاویهٔ C را وتر مینامند (که در شکل روبرو با نماد c نشان داده شدهاست). دو ضلع دیگر که زاویهٔ قائمه را تشکیل میدهند نیز شامل ضلع مجاور زاویهٔ A (و مقابل زاویهٔ B که با حرف b نشان داده میشود) و ضلع مقابل زاویهٔ A (و مجاور زاویهٔ B که با حرف a نشان داده میشود) هستند. به این ترتیب، توابع اصلی مثلثاتی برای زاویهٔ A به صورت زیر تعریف میشوند:[۱۱][۱۲]

- سینوس زاویهٔ A برابر است با نسبت ضلع مقابل آن به وتر. به بیان ریاضی:
- کسینوس زاویهٔ A برابر است با نسبت ضلع مجاور آن به وتر. به بیان ریاضی:
- تانژانت زاویهٔ A نیز به صورت نسبت ضلع مقابل به ضلع مجاور این زاویه محاسبه میشود:
بر پایه قضیهٔ تشابه هندسی، اگر دو مثلث دارای زاویههای برابر باشند، نسبت ضلعهایشان با یکدیگر برابر است. در نتیجه، توابع مثلثاتی که نسبت میان ضلعهای مثلث را نشان میدهند، وابسته به اندازهٔ ضلعها نیستند و مقدار آنها با تغییر اندازهٔ ضلعها تغییر نمیکند.
میتوان برای زاویهٔ B نیز توابع مثلثاتی را به همین ترتیب محاسبه نمود. ضلع مجاور زاویهٔ B (ضلع a) همان ضلع مقابل زاویهٔ A است و ضلع مقابل زاویهٔ B (ضلع b) نیز ضلع مجاور زاویهٔ A میباشد؛ بنابراین میتوان چنین گفت که سینوس زاویهٔ B برابر با کسینوس زاویهٔ A است و برعکس. رابطه سینوس و کسینوس دو زاویهٔ متمم به زبان ریاضی، به صورت زیر است:
با افزایش مقدار زاویهٔ A از صفر تا ۹۰ درجه، به تدریج اندازهٔ ضلع مجاور آن کاهش و اندازهٔ ضلع مقابل، افزایش مییابد. هنگامی که این مقدار به ۹۰ درجه نزدیک شود، مقدار ضلع مجاور به صفر نزدیک میشود. در نتیجه کسینوس زاویهٔ A (نسبت ضلع مجاور به وتر) به صفر میل میکند. از سوی دیگر، مقدار ضلع مقابل به وتر نزدیک میشود. (البته بر پایهٔ قضیهٔ فیثاغورس، وتر همواره از دو ضلع دیگر بزرگتر است) در نتیجه، سینوس زاویهٔ A (نسبت ضلع مقابل به وتر) به ۱ میل میکند. بهطور کلی، مقدار سینوس و کسینوس یک زاویه در مثلث قائمالزاویه، عددی در بازه صفر و یک است. تغییرات تانژانت زاویهٔ A را نیز به همین ترتیب میتوان دنبال کرد. در نزدیکی ۹۰ درجه، تانژانت A (که نسبت سینوس به کسینوس زاویهٔ A است) به سمت بینهایت میل میکند و با نزدیک شدن به صفر، مقدار آن به صفر نزدیک میشود؛ بنابراین مقدار تانژانت یک زاویه، عددی مثبت (از صفر تا بینهایت) خواهد بود.
سه تابع دیگر مثلثاتی را میتوان به عنوان عکس سه تابع بالا تعریف نمود:
| سکانت (معکوس کسینوس): | |
| کسکانت (معکوس سینوس): | |
| کتانژانت (معکوس تانژانت): |
رابطه میان دو زاویهٔ متمم، مانند آنچه که بالاتر در مورد سینوس و کسینوس گفته شد، در مورد سایر توابع مثلثاتی نیز برقرار است.
بهطور خلاصه، رابطهٔ میان توابع مثلثاتی و ضلعهای مثلث قائمالزاویه را میتوان در جدول زیر نشان داد:[۱۳]
| نام | تعریف | رابطه |
|---|---|---|
| سینوس | سینوس یک زاویه برابر است با نسبت ضلع مقابل آن زاویه به وتر | sin A = ضلع مقابل/وتر |
| کسینوس | کسینوس یک زاویه برابر است با نسبت ضلع مجاور آن زاویه به وتر | cos A = ضلع مجاور/وتر |
| تانژانت | تانژانت یک زاویه برابر است با نسبت ضلع مقابل آن زاویه به ضلع مجاور | tan A = ضلع مقابل/ضلع مجاور |
| کتانژانت | کتانژانت یک زاویه برابر است با نسبت ضلع مجاور آن زاویه به ضلع مقابل (عکس تانزانت) | cot A = ضلع مجاور/ضلع مقابل |
| سکانت | سکانت یک زاویه برابر است با نسبت وتر به ضلع مجاور آن زاویه (عکس کسینوس) | sec A = وتر/ضلع مجاور |
| کسکانت | کسکانت یک زاویه برابر است با نسبت وتر به ضلع مقابل آن زاویه (عکس سینوس) | csc A = وتر/ضلع مقابل |
مقدار توابع مثلثاتی برای زاویههای خاص[ویرایش]

برای بعضی زاویهها میتوان به سادگی مقدار توابع مثلثاتی را به دست آورد.[۱۴][۱۵]
در زاویهٔ صفر، سینوس برابر صفر و کسینوس برابر ۱ است؛ در زاویهٔ ۹۰ درجه اما، کسینوس برابر صفر و سینوس برابر ۱ میشود؛ بنابراین:
مثلث قائمالزاویهای که یک زاویهٔ °۴۵ داشته باشد، زاویهٔ تند دیگر آن نیز °۴۵ است و مثلث قائمالزاویهٔ متساویالساقین نامیده میشود. در این مثلث، بر پایه قضیهٔ فیثاغورس اندازه وتر، برابر اندازهٔ هر یک از دو ساق است؛ بنابراین:

با استفاده از ویژگیهای مثلث متساویالاضلاع (شکل روبرو) میتوان نشان داد که ضلع روبرو به زاویهٔ ۳۰ درجه، نصف وتر است؛ بنابراین:
به همین ترتیب، اندازهٔ ضلع دیگر نیز با استفاده از قضیهٔ فیثاغورس برابر به دست میآید. در نتیجه:
سایر توابع مثلثاتی این زاویهها نیز با استفاده از رابطههای دادهشده، محاسبه میشوند.
مقدار توابع مثلثاتی در زاویههای تند در جدول زیر خلاصه شدهاست:
| تابع | ۰° | ۱۵° (π/۱۲) | ۳۰° (π/۶) | ۴۵° (π/۴) | ۶۰° (π/۳) | ۹۰° (π/۲) |
|---|---|---|---|---|---|---|
| سینوس | ||||||
| کسینوس | ||||||
| تانژانت | ||||||
| کتانژانت | ||||||
| سکانت | ||||||
| کسکانت |
یکای اندازهگیری[ویرایش]
| واحد | مقدار | |||||||
|---|---|---|---|---|---|---|---|---|
| درجه | ۰° | ۳۰° | ۴۵° | ۶۰° | ۹۰° | ۱۸۰° | ۲۷۰° | ۳۶۰° |
| رادیان | ۰ | π/۶ | π/۴ | π/۳ | π/۲ | π | ۳π/۲ | ۲π |
| گراد | ۰g | ۱۰۰/۳g | ۵۰g | ۲۰۰/۳g | ۱۰۰g | ۲۰۰g | ۳۰۰g | ۴۰۰g |
| دور | ۰ | ۱/۱۲ | ۱/۸ | ۱/۶ | ۱/۴ | ۱/۲ | ۳/۴ | ۱ |
چند یکای بیبعد برای اندازهگیری زاویه وجود دارد.
- درجه: یکایی است که از گذشتهٔ دور مورد استفاده قرار گرفتهاست. مقدار این یکا با تقسیمبندی یک دایره به ۳۶۰ قسمت مساوی به دست میآید. به بیان دیگر، یک درجه برابر با زاویهٔ روبرو به کمانی است که اندازهٔ آن، ۱/۳۶۰ محیط دایره باشد.
- رادیان: یکای مورد استفاده در محاسبات مربوط به مثلثات است. یک رادیان برابر با زاویهٔ روبرو به کمانی است که طول آن برابر با طول شعاع دایره متناظر باشد. طبق این تعریف، یک دایرهٔ کامل برابر ۲π رادیان (۶٫۲۸۳۲ رادیان) است.[۱۶][۱۷]
- گراد: یک دایرهٔ کامل ۴۰۰ گراد است. به بیان دیگر، گراد یکصدم ربع دایره است. کاربرد عمدهٔ گراد در محاسبات نقشهبرداری است.[۱۸]
- دور: یک دور معادل یک دایرهٔ کامل و برابر با ۳۶۰ درجه یا ۲π رادیان است.
در محاسبات ریاضی که شامل توابع مثلثاتی هستند (مانند معادلات دیفرانسیل و انتگرال)، از یکای رادیان استفاده میشود.[۱۹][۲۰]
تعریف بر پایهٔ دایرهٔ واحد[ویرایش]


شکل روبرو، یک دایرهٔ واحد را نشان میدهد که توابع مثلثاتی زاویهٔ θ روی آن رسم شدهاند. هنگامی که شعاع OA با زاویهٔ θ نسبت به محور افقی روی دایره زده شود، میتوان مقدار توابع مثلثاتی را به صورت اندازهٔ پارهخطهایی مشخص به دست آورد. مقدار توابع سینوس و کسینوس با پارهخطهایی (به ترتیب به رنگ قرمز و آبی) روی دو محور اصلی مختصات رسم شدهاند. به بیان دیگر، تصویر پارهخط OA روی محور افقی برابر با کسینوس θ و تصویر آن روی محور عمودی برابر با سینوس θ است. اندازهٔ پارهخطی (به رنگ قهوهای کمرنگ) که مماس بر دایره از نقطه A تا محور افقی امتداد دارد، تانژانت θ است. امتداد همین پارهخط از نقطه A تا محور عمودی (به رنگ نارنجی) نیز کتانژانت θ را نشان میدهد. به همین ترتیب، میتوان مقدار سکانت و کسکانت زاویهٔ θ را نیز محاسبه کرد.[۲۱]
در دایرهٔ واحد، امکان محاسبهٔ توابع مثلثاتی برای زاویههای بزرگتر از ۹۰ درجه نیز وجود دارد. مقدار توابع مثلثاتی برای هر زاویهای، به شکلی مشابه بالا تعیین میشود. علامت یک تابع بر پایهٔ مقدار زاویه در دایرهٔ واحد بر پایه جدول زیر به دست میآید:[۲۲][۲۳]
| تابع | ربع اول | ربع دوم | ربع سوم | ربع چهارم |
|---|---|---|---|---|
| سینوس کسکانت |
+ | + | – | – |
| کسینوس سکانت |
+ | – | – | + |
| تانژانت کتانژانت |
+ | – | + | – |
دوران[ویرایش]
توابع مثلثاتی برای زاویههای بزرگتر از ۹۰ درجه را میتوان با استفاده از روابط دوران پیرامون مرکز دایره به دست آورد. همچنین زاویههای کوچکتر از صفر با دوران پیرامون محور افقی قابل محاسبه هستند. جدول زیر، نشاندهنده این رابطهها است:
| دوران حول محور افقی[۲۴] | دوران با زاویهٔ π/۲[۲۵] | دوران با زاویهٔ π[۲۶] | دوران با زاویهٔ ۲π[۲۷] |
|---|---|---|---|

تعریف بر پایهٔ انتگرال[ویرایش]
تعریف تابع سینوس توسط مثلث قائم الزاویه از نظر ریاضی دقیق نیست، چرا که مفهوم زاویه (یا همان طول کمان در دایرهٔ واحد) به صورت دقیق بیان نشدهاست. تعریف دیگری را میتوان براساس طول دقیق کمان یک دایره به دست آورد. با در نظر گرفتن معادلهٔ دایره و پیدا کردن طول قوس، میتوان رابطهٔ بین یک زاویه و را برحسب معادلهٔ ضمنی زیر نوشت:[۲۸][۲۹]
که در آن θ زاویهای در محدودهٔ است.
تعریف بر پایهٔ سری توانی[ویرایش]
با استفاده از سری مکلورن هر تابع پیوستهای را میتوان به صورت یک سری توانی حول نقطه صفر (به شکل رابطه زیر) نوشت:[۳۰]
ضریبهای رابطهٔ بالا با معلوم بودن مقدار تابع و مشتقهای آن در نقطه صفر، قابل محاسبه هستند؛ بنابراین میتوان مقدار تقریبی یک تابع را به صورت مجموع یک سری نامتناهی به دست آورد. در محاسبات ریاضی، از جملههای مرتبه بالا (که مرتبه بر اساس دقت محاسبه تعیین میشود) چشمپوشی میکنند.
سری توانی توابع مثلثاتی[ویرایش]
سری توانی توابع مثلثاتی برای محاسبهٔ مقدار تقریبی آنها مورد استفاده قرار میگیرد. در ادامه، سریهای توانی توابع مثلثاتی آورده میشوند.[۳۱]

- سری توانی سینوس و کسینوس
شکل روبرو، نمودار تابع سینوس و بسط مکلورن متناظر با آن را نشان میدهد. مقدار تابع سینوس در نقطه صفر برابر صفر است؛ بنابراین جملههای زوج سری توانی سینوس (که شامل خود تابع و مشتقات مرتبه زوج آن میشوند) صفر هستند. در نتیجه، سری توانی سینوس تنها دارای جملههای با توان فرد خواهد بود.
بهطور مشابه، جملههای فرد سری توانی کسینوس صفر هستند و این سری تنها دارای جملههای با توان زوج است.
تعریف براساس سری توانی این مزیت را دارد که قابل استفاده در اعداد مختلط است و امکان مطالعهٔ خواص تحلیلی بودن این توابع را فراهم میسازد.[۲۸]
- سری توانی سایر توابع مثلثاتی
توابع دیگر مثلثاتی، دارای نقطهٔ تکین در دامنه خود هستند؛ بنابراین نمیتوان سری توانی مکلورن آنها را برای هر مقداری تعریف نمود. برای توابع تانژانت و سکانت که در π/۲ (یا °۹۰) تعریف نمیشوند، دامنه تعریف سری توانی بین π/۲- تا π/۲ است. همچنین برای توابع کتانژانت و کسکانت که در صفر درجه تعریف نمیشوند، دامنه تعریف سری توانی بین صفر تا π میباشد.
استفاده از سریهای توانی[ویرایش]
تعداد جملات سریهای توانی که برای تقریب توابع به کار میروند، نامتناهی است؛ ولی در محاسبات ریاضی از تعداد محدودی از این جملات (بسته به دقت مورد نیاز) استفاده میشود. سایر جملات که محاسبه نمیشوند، جملهٔ باقیمانده یا جملهٔ خطا نامیده میشوند. جملهٔ خطای مرتبهٔ n برای یک سری به صورت زیر تعریف میشود:[۳۲]
با افزایش مقدار x، تعداد بیشتری از جملات برای رسیدن به یک دقت مشخص، مورد نیاز خواهند بود و در نتیجه، سرعت همگرایی کاهش مییابد. افزون بر این، توابع تانژانت، کتانژانت، سکانت و کسکانت دارای نقاط ناپیوستگی هستند و سریهای توانی این توابع تنها برای یک بازهٔ پیوسته تعریف شدهاند.
برای جلوگیری از کند شدن همگرایی و رفع ناپیوستگی توابع، بایستی پیش از بهره گرفتن از سریها زاویه را تا حد امکان کوچک کنیم. با به کار گرفتن اتحادهای مثلثاتی تبدیل زاویه، میتوان زاویه را تا بازهٔ (۰،π/۲) و با استفاده از اتحادهای زاویه متمم تا (۰،π/۴) کاهش داد. به این ترتیب، سرعت همگرایی سری و کارایی محاسبه، افزایش مییابد.[۳۳]
تعریف توسط معادله دیفرانسیل[ویرایش]
یک معادلهٔ دیفرانسیل مرتبهٔ دوم با ضرایب ثابت، به صورت زیر نوشته میشود:
پاسخ این معادله، تابع نمایی به صورت است که در آن، و ریشههای معادلهٔ مشخصهٔ معادله (یعنی ) هستند. همچنین و ثابتهای انتگرالگیری است که بر پایهٔ شرایط اولیه به دست میآیند.
اگر معادلهٔ مشخصه دارای ریشههای مختلط باشد، پاسخ عمومی آن شامل تابع نمایی با توان مختلط است:
که در آن، جزء حقیقی و جزء موهومی ریشهٔ معادلهٔ مشخصه هستند. بر پایهٔ فرمول اویلر، تابع نمایی مختلط به توابع سینوس و کسینوس تبدیل میشود؛ بنابراین در صورت داشتن ریشههای مختلط، پاسخ معادلهٔ دیفرانسیل شامل توابع مثلثاتی خواهد بود:[۳۴]
برای نمونه، هر دو تابع سینوس و کسینوس در معادله دیفرانسیل (با معادله مشخصه که ریشههای آن i± هستند) صدق میکنند.[۳۵] یعنی هر دو، قرینهٔ مشتق دوم خود هستند. به بیان دیگر، این معادلهٔ دیفرانسیل، خانوادهٔ منحنی توابع سینوس و کسینوس را تعریف میکند.[۳۶]
در فضای دوبعدی V، نوع تابع بر پایه شرایط اولیه به صورت زیر تعیین میشود:
- اگر ؛ سینوس، پاسخ یکتای معادله است؛
- اگر ؛ کسینوس، پاسخ یکتای معادله است.
از آنجایی که سینوس و کسینوس، دو تابع مستقل خطی هستند، با یکدیگر تابع پایهٔ V را تشکیل میدهند. این روش تعریف توابع سینوس و کسینوس، معادل با استفاده از فرمول اویلر است.
همچنین تابع تانژانت، پاسخ یکتای معادلهٔ دیفرانسیل غیرخطی با شرط اولیه است.
ویژگیهای توابع مثلثاتی[ویرایش]
- زوج و فرد بودن
بر پایهٔ تعریف توابع مثلثاتی و دایرهٔ واحد، میتوان زوج یا فرد بودن هر تابع مثلثاتی را تعیین نمود. بهطور خلاصه:[۳۷]
- کسینوس و سکانت، تابع زوج هستند. (برای نمونه، )
- سینوس، تانژانت، کتانژانت و کسکانت، تابع فرد هستند. (برای نمونه، )
- تناوب
از تعریف دایرهٔ مثلثاتی و همچنین در جدول بالا مشاهده میشود که توابع مثلثاتی با یک تناوب مشخص، تکرار میشوند. این تناوب برای توابع تانژانت و کتانژانت، °۱۸۰ و برای سایر توابع مثلثاتی، °۳۶۰ است.[۳۸][۳۹] برای نمونه، تناوب توابع سینوس و تانژانت به صورت رابطهٔ زیر است:
در تبدیل فوریه[۴۰] و معادلات موج[۴۱] از این خاصیت تناوبی توابع مثلثاتی در حل معادلات دیفرانسیل استفاده میکنند.
- پیوستگی
توابع سینوس و کسینوس همواره پیوسته و مشتقپذیر هستند. این مطلب، با تعریف بر پایهٔ مثلث قائمالزاویه و تعریف بر پایهٔ دایره واحد، به روشنی قابل ملاحظه است. سایر تابعها که در مخرجشان یکی از دو تابع سینوس یا کسینوس قرار دارد، همواره پیوسته نیستند؛ زیرا مقدار توابع سینوس و کسینوس در برخی نقاط برابر صفر است. نقاط ناپیوستگی توابع مثلثاتی به صورت زیر هستند ( یک عدد صحیح دلخواه است):[۴۲]
- کتانژانت و کسکانت:
- تانژانت و سکانت:
- تعامد
توابع سینوس و کسینوس برهم عمود هستند و در معادله اشتورم-لیوویل صدق میکنند.
همچنین داریم:
از این خواص در محاسبهٔ ضرایب سری فوریه استفاده میشود. [۲۸] [۴۳]
- مشتق و انتگرال توابع مثلثاتی
مشتق دو تابع مثلثاتی اصلی (سینوس و کسینوس) با استفاده از تعریف مشتق، به دست میآید. برای مشتقگیری سایر توابع مثلثاتی میتوان از قاعدهٔ مشتقگیری تابع کسری بهره برد. مشتق اول و دوم توابع مثلثاتی به همراه تابع اولیه (انتگرال) آنها به صورت زیر است:
| تابع | مشتق اول[۴۴] | مشتق دوم | مشتق n-ام[۴۵] | انتگرال[۴۶] |
|---|---|---|---|---|
| پیچیده[۴۷] | ||||
| پیچیده[۴۷] | ||||
| پیچیده[۴۷] | ||||
| پیچیده[۴۷] |
- تبدیلهای لاپلاس و فوریه
تبدیل لاپلاس یکی از روشهای حل معادلات دیفرانسیل است. تبدیل لاپلاس توابع سینوس و کسینوس به صورت زیر است:[۴۸]
- تبدیل سینوس:
- تبدیل کسینوس:
تبدیل فوریهٔ تابعهای سینوس و کسینوس نیز به صورت زیر است:[۴۹]
- تبدیل سینوس:
- تبدیل کسینوس:
که در این روابط نشاندهندهٔ تابع دلتای دیراک است.
- تابع ویژه
توابع سینوس و کسینوس یک تابع ویژه برای لاپلاسین هستند. به عنوان مثال، اگر بیانگر عملگر لاپلاس یک بعدی باشد، توابع سینوس و کسینوس در معادلهٔ صدق میکنند که با توجه به تعریف توسط معادله دیفرانسیل توابع مثلثاتی قابل بررسی است.[۵۰]
روشهای محاسبه[ویرایش]
محاسبهٔ مقدار توابع مثلثاتی به صورت دستی، پیچیدهاست؛ ولی امروزه به دلیل در دسترس بودن رایانهها و ماشین حسابهای مهندسی، که مقدار مورد نیاز را برای هر زاویهای به سادگی به دست میآورند، پیچیدگی آن از بین رفتهاست. سه روش متداول برای محاسبهٔ مقدار توابع مثلثاتی مورد استفاده است که عبارتند از بهرهگیری از مقدارهای دقیق، روش سنتی جدولهای مثلثاتی و روش نوین بهرهگیری از رایانه.
برای بعضی از زاویهها میتوان مقدار دقیق توابع مثلثاتی را به دست آورد. برای نمونه، برای همه زاویههای ضریب °۳ مقدار توابع سینوس، کسینوس و تانژانت به صورت دقیق وجود دارد. نسبتهای مثلثاتی زاویه °۳ با اعمال رابطه تفاضل دو زاویه برای زاویههای °۱۸ و °۱۵ محاسبه میشوند (۳=۱۵–۱۸). نسبتهای مثلثاتی °۱۸ درجه با بهرهگیری از پنجضلعی منتظم به دست میآیند. برای محاسبه نسبتهای مثلثاتی °۱۵ نیز میتوان از اعمال رابطه نصف زاویه برای زاویه °۳۰ استفاده کرد. پس از محاسبه نسبتهای مثلثاتی زاویه °۳، میتوان مقادیر مربوط به زاویههایی که ضریب آن هستند را با استفاده از روابط جمع دو زاویه و زاویه دو برابر، به دست آورد.
برای محاسبهٔ مقدار تابع برای هر زاویهای، نخست باید زاویه را به یک بازه مشخص (مثلاً صفر تا π/۲) کاهش داد. این کار با استفاده از خاصیت تناوب و تقارن توابع مثلثاتی انجام میشود.[۳۳]
پیش از رایانهها، مردم عموماً مقدار توابع مثلثاتی را با درونیابی از دادههای موجود در جدولهای مثلثاتی به دست میآوردند. این جدولها پیشینهای به دیرینگی تاریخ مثلثات دارند. معمولاً مقدارهای موجود در جدولها با استفادهٔ پیاپی از اتحادهای نصف زاویه و مجموع دو زاویه، با آغاز از یک مقدار معلوم (مانند sin(π/۲) = ۱) به دست میآمدند. برای نمونه، میتوان جداول مثلثاتی سینوس و کسینوس خوارزمی را نام برد.[۵۱]
رایانههای نوین، شیوههای گوناگونی را به کار میگیرند.[۵۲] یک روش متداول، به ویژه روی پردازندههای سطح بالا، ترکیب یک تقریب چندجملهای یا کسری (مانند تقریب چبیشف، تقریب پد و معمولاً برای دقتهای بالاتر، سری تیلور و مکلورن) با کاهش بازه و نگاه به جدول است. (با استفاده از جدول، نزدیکترین زاویه انتخاب میشود، سپس تصحیح با بهرهگیری از چندجملهای انجام میشود) دستگاههای دارای دقت پایینتر، معمولاً از الگوریتم CORDIC سود میبرند که تنها از جمع، تفریق، شیفت بیتی و نگاه به جدول استفاده میکند.
برای محاسبات بسیار دقیق، که سریها به کندی همگرا میشوند، میتوان از میانگین حسابی-هندسی برای تقریب استفاده کرد که تابع مثلثاتی را با انتگرال بیضوی تقریب میزند.[۵۳]
اتحادهای مثلثاتی[ویرایش]
بعضی از رابطههای مثلثاتی برای هر زاویهٔ دلخواهی برقرار هستند. این رابطهها را اتحاد مثلثاتی مینامند. نمونههایی از این اتحادها در زیر آورده میشوند.
- قضیهٔ فیثاغورس
سادهترین شکل قضیهٔ فیثاغورس در مثلثات به صورت زیر است:[۵۴]
- جمع و تفاضل دو زاویه
کسینوس حاصل جمع:[۵۵]
سینوس حاصل جمع:[۵۶]
- زاویهٔ دو برابر
رابطههای زیر برای محاسبهٔ سینوس و کسینوس زاویهای دو برابر زاویهٔ معلوم به کار میروند:[۵۷]
- قضیهٔ فشردگی سینوس
یک نابرابری مهم مثلثاتی، در محاسبهٔ حدهای مبهم و مشتق توابع مثلثاتی کاربرد دارد. این نابرابری که در بازهٔ -π/۲<θ<π/۲ معتبر است، به صورت زیر است:[۵۸]
با کمک این نابرابری و استفاده از قضیهٔ فشردگی، حد مبهم محاسبه میشود.[۵۹] این حد در محاسبهٔ مشتق توابع مثلثاتی مورد استفاده قرار میگیرد.[۶۰]
نابرابریهایی مشابه به شرح زیرند:[۶۱]
- قانون سینوسها
با استفاده از قانون سینوسها در هر مثلث دلخواه، میتوان با معلوم بودن اندازه یک ضلع و دو زاویهٔ مجاور آن، اندازهٔ دو ضلع دیگر را محاسبه نمود. همچنین میتوان مساحت مثلث (Δ) و شعاع دایرهٔ محیطی آن (R) را به دست آورد:[۶۲]
بر اساس اتحاد بالا، مساحت مثلث با معلوم بودن اندازهٔ دو ضلع و زاویهٔ میان آنها از رابطهٔ زیر، قابل محاسبه است:
- قانون کسینوسها
با استفاده از قانون کسینوسها در هر مثلث دلخواه، با معلوم بودن اندازهٔ دو ضلع و زاویهٔ میان آنها، اندازهٔ ضلع سوم به صورت زیر تعیین میشود:[۶۳]
همچنین با این قانون میتوان با داشتن اندازهٔ سه ضلع مثلث، اندازهٔ زاویههای آن را به دست آورد.
- رابطه توابع مثلثاتی با توابع خاص
بعضی از توابع خاص را میتوان به صورت ترکیبی از توابع از جمله توابع مثلثاتی نوشت.
- تابع بسل مرتبهٔ ۱/۲: تابع بسل، پاسخ معادلهٔ دیفرانسیل مرتبهٔ دوم زیر است:
که a مرتبهٔ آن را نشان میدهد. حل این معادله، به صورت سری توانی است. میتوان یکی از حالتهای خاص تابع بسل (a=۱/۲) را برحسب توابع مثلثاتی به صورت زیر نوشت:[۶۴]
- چندجملهای چبیشف: چندجملهای چبیشف، پاسخ معادلهٔ دیفرانسیل مرتبهٔ دوم زیر است:
که n مرتبهٔ آن را نشان میدهد. میتوان چندجملهای چبیشف مرتبهٔ n را برحسب توابع مثلثاتی به صورت زیر نوشت:[۶۵]
تابع معکوس[ویرایش]
توابع معکوس مثلثاتی به عنوان قرینهٔ توابع مثلثاتی نسبت به خط y=x تعریف میشوند. این تابعها را با افزودن آرک به ابتدای نام تابع اصلی، معرفی میکنند. این تابعها یک عدد حقیقی را میگیرند و یک زاویه را برمیگردانند.
توابع مثلثاتی در همهٔ دامنهٔ خود، یکبهیک و معکوسپذیر نیستند. برای آن که بتوان تابع معکوس برای این توابع تعریف نمود، باید تابع به دامنهای که در آن معکوسپذیر است، محدود شود. این دامنه، برای توابع مختلف به صورت جدول زیر است. افزون بر این، مشتق توابع معکوس مثلثاتی که با روش مشتقگیری ضمنی به دست میآید، در جدول آورده شدهاست.[۶۶]
| تابع اصلی | دامنهٔ تابع اصلی | تابع معکوس | دامنهٔ تابع معکوس | مشتق تابع معکوس[۶۷] |
|---|---|---|---|---|
| اعداد حقیقی | ||||
| اعداد حقیقی | ||||
کاربرد[ویرایش]
توابع مثلثاتی کاربردهای قابل توجهی در بسیاری از علوم پایه و مهندسی دارند.
فضای برداری[ویرایش]
در ریاضیات و فیزیک، از بردارها برای نشان دادن یک کمیت برداری (که دارای اندازه و جهت است) استفاده میشود. بسیاری از کمیتهای اصلی فیزیک مانند مکان، نیرو و میدان دارای ماهیت برداری هستند. در برخی محاسبات فضای برداری از توابع مثلثاتی استفاده میشود. برای نمونه، ضرب داخلی دو بردار x و y متعلق به ℝ۳ را میتوان به کمک قانون کسینوسها به صورت زیر محاسبه کرد:[۶۸]
همچنین برای محاسبهٔ ضرب خارجی آنها نیز میتوان رابطهٔ زیر را به کار بست:
مختصات قطبی، استوانهای و کروی[ویرایش]

توابع مثلثاتی، پایهٔ تعریف دستگاه مختصات قطبی هستند که در سادهسازی بسیاری از مسائل ریاضیات و فیزیک از جمله برخی انتگرالها مؤثر است. در این دستگاه مختصات، به جای طول و عرض (x,y) یک نقطه (که در دستگاه مختصات دکارتی به کار میرود)، فاصلهٔ آن با مرکز و زاویهٔ بردار گذرنده از مرکز و آن نقطه نسبت به خط افقی (r,θ) به عنوان مختصات یک نقطه در نظر گرفته میشوند.[۶۹] تبدیل مختصات دکارتی به مختصات قطبی و برعکس با استفاده از توابع مثلثاتی انجام میشود:[۷۰]
دستگاههای مختصات استوانهای[۷۱] و کروی[۷۲] که تعمیمیافتهٔ مختصات قطبی در سهبعد هستند نیز بر مبنای توابع مثلثاتی شکل گرفتهاند. از این دستگاهها در مسائلی مانند انتگرالهای سهبعدی که دارای تقارن استوانهای یا کروی هستند استفاده میشود.
اعداد مختلط[ویرایش]

با استفاده از تعریف مختصات قطبی میتوان اعداد مختلط را به صورت توابع مثلثاتی بیان کرد:[۷۳]
که در آن، |z| اندازهٔ بردار z (فاصله از مبدأ)، θ زاویهٔ آن با محور افقی، و i بیانگر یکهٔ موهومی است. افزون بر این، رابطهٔ میان تابع نمایی و تابع مثلثاتی توسط فرمول اویلر برقرار میشود:[۷۴]
که بر پایهٔ آن، توابع سینوس و کسینوس به شکل توابع فرد و زوج متناظر بر حسب تابع نمایی نوشته میشوند:
مشاهده میشود که میتوان کسینوس را به عنوان جزء حقیقی و سینوس را به عنوان جزء مجازی تابع نمایی مختلط در نظر گرفت. به بیان ریاضی:
شکل توسعهیافتهٔ فرمول اویلر، به عنوان فرمول دموآور شناخته میشود:[۷۵]
همچنین با استفاده از تعریف بسط مکلورن برای توابع هذلولوی و مثلثاتی، میتوان رابطههای زیر را که معادل با رابطههای بالا هستند، به دست آورد:
که در آنها i2=−۱. میتوان توابع سینوس و کسینوس مختلط را برحسب اجزای حقیقی و مجازی آنها نیز نوشت:[۷۶]
این اتحاد، رابطهٔ میان توابع سینوس و کسینوس مختلط و توابع حقیقی (سینوس و کسینوس) و حقیقی هذلولوی (سینوس هذلولوی و کسینوس هذلولوی) آنها را نشان میدهد.
نقشهبرداری[ویرایش]
مثلثات، پایهٔ بیشتر شیوههای نقشهبرداری است. زاویهیابی با دستگاه یا بدون دستگاه، امتدادیابی با روش ژیزمان، سیستم تصویر برای تبدیل تصویر از سطح بیضوی به سطح مستوی، ارتفاعیابی با دستگاه ترازیاب، پیمایش باز و بسته، طراحی قوسها در راهسازی و تبدیلهای دوبعدی در نقشهبرداری هوایی، بخشی از کاربردهای توابع مثلثاتی در نقشهبرداری هستند.
برای نمونه، در مثلثسازی که یکی از روشهای قدیمی نقشهبرداری است، با استفاده از اندازهگیری زاویهٔ یک نقطه نسبت به دو نقطه معین، مختصات آن نقطه را محاسبه میکنند که امروزه از این روش برای اندازهگیری سهبعدی نوری استفاده میشود. در مثلثسازی از قانون کسینوسها و قانون سینوسها برای محاسبهٔ زاویهٔ مثلثها و تعیین دقیق موقعیت هر نقطه استفاده میشود.
پیمایش روشی برای نقشهبرداری یک محدودهٔ باز یا بسته با استفاده از اندازهگیری زاویهها و فاصلهها است. از توابع مثلثاتی برای محاسبهٔ موقعیت ایستگاهها استفاده میشود.[۷۷]
ناوبری[ویرایش]
از توابع مثلثاتی در زمینههای مختلف ناوبری استفاده میشود. برای نمونه، تنظیم خط سیر کشتیها و سایر شناورها بر پایهٔ اجسام ثابت مانند فانوس دریایی با بهرهگیری از توابع مثلثاتی انجام میشود.[۷۸] همچنین این توابع برای تعیین فاصلهٔ میان دو نقطه روی زمین با در نظر گرفتن کرویت زمین به کار میروند. رابطهٔ زیر برای محاسبهٔ این فاصله مورد استفاده قرار میگیرد:
که در آن، α۱ و α۲ عرض جغرافیایی دو نقطهٔ مورد نظر و φ اختلاف طول جغرافیایی میان دو نقطه است.[۷۹]
فیزیک نور[ویرایش]
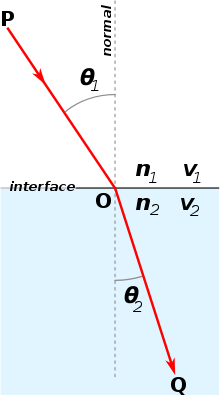
بنیادیترین کاربرد توابع مثلثاتی در نورشناسی، قانون اسنل است. این قانون که در پدیدهٔ شکست نور به کار میرود، رابطهٔ میان زاویهٔ نور در یک محیط و زاویهٔ آن پس از وارد شدن به یک محیط دیگر با ضریب شکست متفاوت را بیان میکند:
که در آن، n و 'n ضریب شکست و θ و 'θ زاویهٔ پرتو نور محیط اول و دوم هستند. قانون اسنل، در تعیین زاویهٔ حد شکست و نیز در شکست نور در منشورها و عدسیها به کار میرود. مسیر حرکت نور در عبور از یک عدسی با استفاده از قانون اسنل تعیین میشود.
افزون بر شکست نور، از توابع مثلثاتی در زمینههای دیگری از نورشناسی مانند تحلیل تداخل امواج، قطبیدگی و پراش در دو شکاف استفاده میشود.[۸۰]
سری فوریه و تبدیل فوریه[ویرایش]
توابع سینوس و کسینوس مانند چندجملهایها متعامد هستند و استقلال خطی دارند. از این رو میتوان هر تابع (عموماً متناوب) را بر حسب یک سری از این توابع به صورت رابطهٔ زیر نوشت[۸۱] که سری فوریه نامیده میشود:[۸۲]
برای توابع فرد، تنها جملات تابع سینوس و برای توابع زوج، تنها جملات تابع کسینوس و ضریب ثابت در نظر گرفته میشوند.[۸۳]
تبدیل فوریه، نوعی تبدیل انتگرالی است که شکل توسعه یافتهٔ سری فوریه است. این تبدیل به صورت زیر تعریف میشود:[۸۴]
که تابع نمایی با نمای مختلط توسط فرمول اویلر به توابع مثلثاتی تبدیل میشود. از تبدیل فوریه در حل معادلات دیفرانسیل جزئی از جمله معادلهٔ موج، تحلیل طیفی و پردازش سیگنال بهره میبرند.[۸۵]
همچنین در ذخیرهسازی تصویر با قالب JPEG از تبدیل کسینوس گسسته برای کاهش حجم تصویر با وجود حفظ نسبی کیفیت آن استفاده میکنند. در این روش، تصویر به بلوکهایی با ابعاد یکسان تقسیم میشود و در هر بلوک، ضرایب چند جملهٔ نخست تبدیل فوریه (که تعداد جملهها بر پایهٔ دقت تبدیل، انتخاب میشود) بر پایهٔ رنگ همهٔ نقطههای درون بلوک محاسبه میشوند.[۸۶]
حرکت نوسانی[ویرایش]

فیزیکدانان برای توصیف حرکت هماهنگ ساده، از توابع سینوس و کسینوس استفاده میکنند. این حرکت، بسیاری از پدیدههای فیزیکی مانند حرکت جرم متصل به فنر،[۸۷] حرکت آونگی جسم معلق با یک طناب (پاندول ساده)،[۸۸] تحلیل مدار الکتریکی[۸۹] و حرکت دایرهای یکنواخت یکبعدی را مدل میکند. همچنین توابع مثلثاتی در مطالعهٔ توابع متناوب به کار میروند. ساختار موجیشکل توابع متناوب برای مدلسازی پدیدههای رفت و برگشتی مانند نور، صدا و موج دریا، مورد استفاده قرار میگیرد.
در شرایط عمومی، میتوان یک تابع متناوب (f(x را با سری فوریه به صورت مجموع موجهای سینوسی یا موجهای کسینوسی بیان کرد. اگر تابع سینوس یا کسینوس را با φk نشان دهیم، بسط تابع متناوب (f(t به صورت زیر خواهد بود (از آنجایی که توابع متناوب عموماً بر حسب زمان تعریف میشوند، در اینجا به جای متغیر مکانی (x) از متغیر زمانی (t) استفاده میشود):
برای نمونه، موج مربعی را میتوان با سری فوریه زیر نشان داد:
همان گونه که در شکل روبرو دیده میشود، چند جملهٔ اول سری میتوانند تقریب نسبتاً خوبی را ایجاد کنند.
فیزیک مکانیک[ویرایش]
در فیزیک مکانیک، توابع مثلثاتی در معادلات حرکت دوبعدی و سهبعدی کاربرد دارند. برای نمونه، در تحلیل تغییرات تناوبی در سینماتیک و دینامیک دورانی، معادلات تکانه و تکانهٔ زاویهای و پدیدهٔ برخورد، توابع مثلثاتی کاربرد دارند.[۹۰]
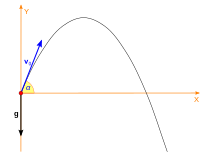
یکی از آشناترین کاربردهای توابع مثلثاتی در مکانیک، پدیدهٔ حرکت پرتابی است که معادلات حرکت افقی و قائم آن به صورت زیر نوشته میشود:
که در آن، x و y مختصات موقعیت ذره در مدت t ثانیه پس از پرتاب با سرعت اولیهٔ v0 هستند.
همچنین مسیر و سرعت دو ذره پس از برخورد کشسان مایل، با استفاده از توابع مثلثاتی به دست میآید.
برق و مخابرات[ویرایش]

امروزه جریانهای متناوب در صنعت برق کاربرد گستردهای دارند و شکل رایج آنها به صورت موج سینوسی است. از دلایل اصلی محبوبیت جریانهای متناوب نسبت به جریان مستقیم در صنعت بر میتوان به امکان تبدیل سطح ولتاژِ جریانهای متناوب با استفاده از ترانسفورماتورها که به واسطهٔ آن میتوان تلفات را برای انتقال در مسافتهای طولانی کاهش داد و نیز عدم نیاز به استفاده از کموتاتور در ژنراتورهای القایی اشاره کرد.[۹۱]
نیروگاهها اغلب توان را در به صورت سهفاز (سه ولتاژ سینوسی با اختلاف زاویهٔ ۱۲۰°) تولید میکنند. شکل موجهای ولتاژ و جریان به منظور سادگی اغلب ایدئال و به صورت و فرض میشوند و به تبع آن روابط مختلف، مثل توان لحظهای، توان اکتیو، توان راکتیو، و… یا مفاهیمی مانند پیشفازی، پسفازی، زاویهٔ توان و ضریب قدرت و … با تحلیل توابع مثلثاتی محاسبه و تعریف میشوند.[۹۲] برق ارائهشده به مشترکان خانگی با شکل موج سینوسی و عموماً در فرکانسهای ۵۰ یا ۶۰ هرتز ارائه میشود.[۹۳]
در مدلسازی خطوط بلند انتقال نیرو، پارامترهای خط را توابع هذلولی مثلثاتی مدلسازی میکنند.[۹۴]
کاربرد موجهای سینوسی در برق به قدری گستردهاست که برای تحلیل آنها روشهای خاصی که مؤثرتر هستند ابداع شدهاست.[۹۵] تحلیل فازور روشی است که در آن با استفاده از این خاصیت که مجموع جبری هر تعداد موج سینوسی با فرکانس زاویهای یکسان و مشتقهای مرتبههای مختلف آنها همواره یک موج سینوسی با همان فرکانس زاویهای خواهد بود، برای نمایش و تحلیل موج سینوسی تنها از دامنه و فاز آن استفاده میشود. با این کار برای به دست آوردن پاسخ حالت دائمی سینوسی، به جای حل معادلهٔ دیفرانسیل، تنها به حل معادلات جبری ساده نیاز خواهد بود. با استفاده از این مفهوم میتوان پاسخ حالت دائمی سینوسی یک مدار خطی تغییرناپذیر با زمان را مستقیماً با حل شبکهٔ معادلی که بر حسب فازورهای ورودی، خروجی و فازور متغیرهای دیگر بیان شدهاست با استفاده از روشهای جبری به دست آورد.[۹۶]
در سیستمهای مخابراتی، معمولاً کانال ارتباطی تنها در یک گسترهٔ فرکانسی خاص سیگنالها را به خوبی منتقل میکند که در خارج از این گستره انتقال سیگنال ناممکن یا همراه با افت شدید کیفیت است. به همین دلیل برای فرستادن یک سیگنال در مسافتهای طولانی معمولاً آن را روی یک سیگنال فرکانس بالای دیگر سوار میکنند که به این کار مدولاسیون گفته میشود.[۹۷] سیگنال حامل در روشهای مختلف مدولاسیون اغلب ذاتاً یک موج سینوسی است.[۹۸] برای مثال در مدولاسیون دامنهٔ سینوسی، سیگنال حاوی اطلاعات در سیگنال حامل سینوسی ضرب (مدوله) میشود.[۹۹]
پانویس[ویرایش]
- ↑ دانتزیگ، توبیاس (۱۳۵۶). میراث یونان. ترجمهٔ عباس گرمان. توکا.
- ↑ ۲٫۰ ۲٫۱ ۲٫۲ ۲٫۳ ۲٫۴ بویر، کارل (۱۳۸۴). تاریخ حسابان. ترجمهٔ عبدالحسین مصحفی. علمی و فرهنگی. شابک ۹۶۴-۴۴۵-۶۹۸-X.
- ↑ استرویک، تاریخ فشرده ریاضیات، ۷۵.
- ↑ استرویک، تاریخ فشرده ریاضیات، ۸۶.
- ↑ استرویک، تاریخ فشرده ریاضیات، ۹۲.
- ↑ استرویک، تاریخ فشرده ریاضیات، ۹۳.
- ↑ قربانی، زندگینامهٔ ریاضیدانان دورهٔ اسلامی از سدهٔ سوم تا سدهٔ یازدهم هجری، ۳۶۸.
- ↑ Victor J. Katz (November 1987). "The calculus of the trigonometric functions". Historia Mathematica (به انگلیسی). 14: 311–324. doi:10.1016/0315-0860(87)90064-4. Archived from the original on 16 May 2015.
- ↑ علیاکبر دهخدا و دیگران، «جیب» در لغتنامهٔ دهخدا (بازیابیشده در ۱۵ مه ۲۰۱۵).
- ↑ نوری، نیر (۱۳۷۵–۱۳۷۷). سهم ارزشمند ایران در فرهنگ جهان. تهران: انجمن آثار و مفاخر فرهنگی. صص. ۲۴۰. شابک ۹۶۴۶۲۷۸۲۰۵.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۵۳.
- ↑ آدامز، حساب دیفرانسیل و انتگرال، جلد اول، ۱۴۶.
- ↑ برای نمونه:سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، ۸۶–۸۷. و توماس، حسابان، ۵۰.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، جلد اول، ۹۱.
- ↑ توماس، حسابان، ۵۰.
- ↑ توماس، حسابان، ۴۸.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، ۸۹.
- ↑ Lindeburg, Michael R. (2012), Civil Engineering Reference Manual for the PE Exam, Professional Publications, Inc., p. 78-7, ISBN 978-1-59126-380-7
- ↑ توماس، حسابان، ۵۰.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، ۸۹.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۲۸۵.
- ↑ توماس، حسابان، ۵۰.
- ↑ آبراموویچ و استگان، راهنمای توابع ریاضی با روابط، نمودارها و جدولهای ریاضی، ۷۳.
- ↑ توماس، حسابان، ۵۳.
- ↑ آبراموویچ و استگان، راهنمای توابع ریاضی با روابط، نمودارها و جدولهای ریاضی، ۷۳.
- ↑ آبراموویچ و استگان، راهنمای توابع ریاضی با روابط، نمودارها و جدولهای ریاضی، ۷۳.
- ↑ توماس، حسابان، ۵۲.
- ↑ ۲۸٫۰ ۲۸٫۱ ۲۸٫۲ Gowers, T.; Barrow-Green, J.; Leader, I. (2010). The Princeton Companion to Mathematics (به انگلیسی). Princeton University Press. p. ۳۰۷–۳۰۸. Archived from the original on 16 May 2015. Retrieved 2015-05-05.
- ↑ Trigonometric functions. V.I. Bityutskov (originator), Encyclopedia of Mathematics.
- ↑ توماس، حسابان، ۸۰۶.
- ↑ آبراموویچ و استگان، راهنمای توابع ریاضی با روابط، نمودارها و جدولهای ریاضی، ۷۴–۷۵.
- ↑ توماس، حسابان، ۸۱۲.
- ↑ ۳۳٫۰ ۳۳٫۱ Robin Green. "Faster Math Functions" (PDF). pp. 6–7. Archived from the original (PDF) on 16 May 2015. Retrieved April 10, 2015.
- ↑ بویس و دیپریما، معادلات دیفرانسیل مقدماتی و مسائل مقدار مرزی، ۱۸۷–۱۸۸.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، ۲۲۷.
- ↑ کرایهچیان، معادلات دیفرانسیل و کاربرد آنها، ۱۹–۲۰.
- ↑ توماس، حسابان، ۵۳.
- ↑ توماس، حسابان، ۵۳.
- ↑ آدامز، حساب دیفرانسیل و انتگرال، جلد اول، ۱۳۸.
- ↑ توماس، حسابان، ۸۳۳–۸۳۵.
- ↑ توماس، حسابان، ۹۹۶.
- ↑ توماس، حسابان، ۵۰.
- ↑ Olver, NIST Handbook of Mathematical Functions, 122.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، جلد اول. تابع سینوس و کسینوس: ص. ۱۷۹؛ سایر تابعها: صص. ۲۱۰–۲۱۱
- ↑ آبراموویچ، راهنمای توابع ریاضی با روابط، نمودارها و جدولهای ریاضی، ۷۷.
- ↑ توماس، حسابان، ۵۵۴.
- ↑ ۴۷٫۰ ۴۷٫۱ ۴۷٫۲ ۴۷٫۳ EG Wintucky (ژوئیه ۱۹, ۱۹۷۱). «FORMULAS FOR nth ORDER DERIVATIVES OF HYPERBOLIC. AND TRIGONOMETRIC FUNCTIONS» (PDF). NASA. دریافتشده در مه ۱۸, ۲۰۱۵.
- ↑ بویس و دیپریما، معادلات دیفرانسیل مقدماتی و مسائل مقدار مرزی، ۳۷۶.
- ↑ Kammler, D.W. (2008). A First Course in Fourier Analysis (به انگلیسی). Cambridge University Press. Archived from the original on 17 اكتبر 2018. Retrieved 2015-05-12.
{{cite book}}: Check date values in:|تاریخ بایگانی=(help) - ↑ Pivato, M. (2010). Linear Partial Differential Equations and Fourier Theory (به انگلیسی). Cambridge University Press. p. 243. Archived from the original on 16 May 2015. Retrieved 2015-05-10.
- ↑ استرویک، تاریخ فشرده ریاضیات، ۹۲.
- ↑ Kantabutra, Vitit (1996). "On hardware for computing exponential and trigonometric functions". IEEE Trans. Computers. 45 (3): 328–339.
- ↑ Brent, Richard P. (April 1976). "Fast Multiple-Precision Evaluation of Elementary Functions". J. ACM. 23 (2): 242–251. Archived from the original on 16 May 2015. Retrieved 2 April 2015.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، جلد اول، ۸۸.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۱۵۲–۱۵۴.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۱۵۸–۱۵۹.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۱۶۷–۱۶۸.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، جلد اول، ۱۰۵–۱۰۶.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، جلد اول، ۱۳۸.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، جلد اول، ۱۷۹–۱۸۰.
- ↑ Olver, NIST Handbook of Mathematical Functions, 116.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۱۸۹–۱۹۰.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۱۹۴–۱۹۵.
- ↑ کرایهچیان، معادلات دیفرانسیل و کاربرد آنها، ۲۳۴–۲۳۵.
- ↑ نووسلو، مثلثات مستقیمالخط و کروی، ۳۲۲–۳۲۳.
- ↑ سیلورمن، حساب دیفرانسیل و انتگرال با هندسه تحلیلی، جلد اول، ۴۶۵–۴۷۴.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۲۴۴، ۲۴۵، ۲۵۱.
- ↑ هالیدی، رسنیک و کرین، فیزیک.
- ↑ توماس، حسابان، ۷۱۴.
- ↑ توماس، حسابان، ۷۱۶.
- ↑ آدامز، حساب دیفرانسیل و انتگرال، جلد دوم، ۳۹۴–۳۹۶.
- ↑ آدامز، حساب دیفرانسیل و انتگرال، جلد دوم، ۳۹۶–۴۰۱.
- ↑ توماس، حسابان، AP-17.
- ↑ آبراموویچ و استگان، راهنمای توابع ریاضی با روابط، نمودارها و جدولهای ریاضی، ۱۶.
- ↑ آبراموویچ و استگان، راهنمای توابع ریاضی با روابط، نمودارها و جدولهای ریاضی، ۷۴.
- ↑ Mathews, J.H.; Howell, R.W. (2006). Complex Analysis for Mathematics and Engineering (به انگلیسی). Jones and Bartlett. p. ۱۷۸–۱۷۹. Retrieved 2015-05-18.
- ↑ عاصی، محمدرضا (۱۳۸۸). نقشهبرداری (ژئوماتیک) (ویراست چهارم). انتشارات علمی دانشگاه ضنعتی شریف. شابک ۹۷۸-۹۶۴-۲۰۸-۰۰۸-۳.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۶۶–۶۷.
- ↑ کاکسفورد، اصول و کاربردهای مثلثات، ۲۵۶–۲۵۷.
- ↑ جنکینز، فرانسیس ای.؛ وایت، هاردی ای. (۱۳۸۹). مبانی اپتیک. ترجمهٔ بابک حقیقی. نشر مرندیز. شابک ۹۷۸-۶۰۰-۱۰۶-۰۵۶-۴.
- ↑ توماس، حسابان، ۸۳۳–۸۳۵.
- ↑ Bary، A Treatise on Trigonometric Series، 43.
- ↑ Bary، A Treatise on Trigonometric Series، 50.
- ↑ Weisstein, Eric W. "Fourier Transform" (به انگلیسی). Mathworld. Archived from the original on 16 May 2015. Retrieved May 16, 2015.
- ↑ Gerald B Folland (2009). "Convergence and completeness". Fourier Analysis and its Applications (Reprint of Wadsworth & Brooks/Cole 1992 ed.). American Mathematical Society. p. 225-234. ISBN 0-8218-4790-2. Archived from the original on 16 May 2015. Retrieved 10 May 2015.
- ↑ "(JPEG (Transform Compression". The Scientist and Engineer's Guide to Digital Signal Processing. Archived from the original on 16 May 2015. Retrieved March 29, 2015.
- ↑ بویس و دیپریما، معادلات دیفرانسیل مقدماتی و مسائل مقدار مرزی، ۲۳۰–۲۳۹.
- ↑ کرایهچیان، معادلات دیفرانسیل و کاربرد آنها، ۱۶۶–۱۶۹.
- ↑ برای نمونه بویس و دیپریما، معادلات دیفرانسیل مقدماتی و مسائل مقدار مرزی، ۲۴۰–۲۴۱.
- ↑ هالیدی، رسنیک و کرین، فیزیک.
- ↑ سعادت، بررسی سیستمهای قدرت (جلد اول)، ۱.
- ↑ سعادت، «اصول مقدماتی»، بررسی سیستمهای قدرت (جلد اول)، ۱۹–۶۰.
- ↑ سعادت، بررسی سیستمهای قدرت (جلد اول)، ۱–۲.
- ↑ سعادت، بررسی سیستمهای قدرت (جلد اول)، ۱۹۸.
- ↑ دسور و کوه، نظریه اساسی مدارها و شبکهها - جلد اول، ۴۱۱.
- ↑ دسور و کوه، نظریه اساسی مدارها و شبکهها - جلد اول، ۴۱۴–۴۳۱.
- ↑ اوپنهایم ، ویلسکی و نواب، «سیستمهای مخابراتی»، سیگنالها و سیستمها، ۵۲۷.
- ↑ Mahalik, Sensor Networks and Configuration: Fundamentals, Standards, Platforms, and Applications, 487.
- ↑ اوپنهایم ، ویلسکی و نواب، «سیستمهای مخابراتی»، سیگنالها و سیستمها، ۵۲۸.
منابع[ویرایش]
- آدامز، رابرت (۱۳۸۸). حساب دیفرانسیل و انتگرال، جلد اول. ترجمهٔ سید حسین اورعی. انتشارات دانشگاه فردوسی مشهد. شابک ۹۶۴-۳۸۶-۰۱۵-۹.
- آدامز، رابرت (۱۳۸۸). حساب دیفرانسیل و انتگرال، جلد دوم. ترجمهٔ سید حسین اورعی. انتشارات دانشگاه فردوسی مشهد. شابک ۹۶۴-۳۸۶-۰۶۸-X.
- استرویک، درک (۱۳۶۶). تاریخ فشرده ریاضیات. ترجمهٔ غلامرضا برادران خسروشاهی، حشمتالله کامرانی. نشر نو.
- بویس، ویلیام ای.؛ دیپریما، ریچارد سی. (۱۳۸۴). معادلات دیفرانسیل مقدماتی و مسائل مقدار مرزی. ج. اول. ترجمهٔ علیاکبر عالمزاده (ویراست هفتم). انتشارات علمی و فنی. شابک ۹۷۸-۹۶۴-۶۲۱۵-۳۵-۱.
- سیلورمن، ریچارد (۱۳۸۶). حساب دیفرانسیل و انتگرال با هندسه تحلیلی، جلد اول. ترجمهٔ علیاکبر عالمزاده. انتشارات ققنوس. شابک ۹۷۸-۹۶۴-۳۱۱-۰۰۵-۵.
- قربانی، ابوالقاسم (۱۳۷۵). زندگینامهٔ ریاضیدانان دورهٔ اسلامی از سدهٔ سوم تا سدهٔ یازدهم هجری. تهران: مرکز نشر دانشگاهی. شابک ۹۶۴-۰۱-۰۸۱۷-۰.
- کاکسفورد، آرتور (۱۳۷۰). اصول و کاربردهای مثلثات. ترجمهٔ عادل ارشقی. انتشارات رسا.
- کرایهچیان، علیاصغر (۱۳۸۶). معادلات دیفرنسیل و کاربرد آنها. انتشارات دانشگاه فردوسی مشهد. شابک ۹۶۴-۶۳۳۵-۱۳-۶.
- لیتهولد، لوئیس (۱۳۸۷). حساب دیفرانسیل و انتگرال با هندسه تحلیلی. ترجمهٔ علیاکبر عالمزاده. تهران: علوم نوین. شابک ۹۷۸-۹۶۴-۶۱۳۳-۰۳-۷.
- نووسلو، سرگی ایوسیفویچ (۱۳۶۵). مثلثات مستقیمالخط و کروی. ترجمهٔ پرویز شهریاری. انتشارات امیرکبیر.
- هالیدی، دیوید؛ رسنیک، رابرت؛ کرین، کنت اس. (۱۳۸۸). فیزیک. ج. اول، مکانیک. ترجمهٔ محمد موسوی بایگی (ویراست پنجم). مرکز نشر دانشگاهی. شابک ۹۶۴-۵۷۷۷-۵۵-۰.
- سعادت، هادی (۱۳۹۲). بررسی سیستمهای قدرت (جلد اول). ترجمهٔ احد کاظمی، شهرام جدید و حیدرعلی شایانفر. دانشگاه علم و صنعت ایران. شابک ۹۶۴-۴۵۴-۳۹۴-۷.
- دسور، چارلز؛ کوه، ارنست (۱۳۹۲). نظریه اساسی مدارها و شبکهها - جلد اول. ترجمهٔ پرویز جبه دارمارالانی. دانشگاه تهران. شابک ۹۷۸-۹۶۴-۰۳-۴۲۴۸-۰.
- اوپنهایم، آلن؛ ویلسکی، آلن؛ نواب، حمید (۱۳۸۴). سیگنالها و سیستمها. ترجمهٔ محمود دیانی. نص. شابک ۹۶۴-۶۲۶۴-۲۸-X.
- Abramowitz, M. and Stegun, I. A. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing (به انگلیسی). New York: Dover. p. 16.
{{cite book}}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - Bary, N. K. (1964). A Treatise on Trigonometric Series (به انگلیسی). Vol. I. New York: The Macmillan Company.
- Thomas, George B. Jr (2009). Calculus (به انگلیسی). Pearson. Archived from the original on 16 May 2015.
- Olver, F.W.J. (2010). NIST Handbook of Mathematical Functions (به انگلیسی). Cambridge University Press. Archived from the original on 16 May 2015. Retrieved 2015-05-10.
- Mahalik, N.P. (2007). Sensor Networks and Configuration: Fundamentals, Standards, Platforms, and Applications (به انگلیسی). Springer Berlin Heidelberg. Archived from the original on 16 May 2015. Retrieved 2015-05-16.
پیوند به بیرون[ویرایش]
| ویکیکتاب دارای کتابی پیرامون موضوع توابع مثلثاتی است |
| در ویکیانبار پروندههایی دربارهٔ توابع مثلثاتی موجود است. |




































































































































































































