خروج از مرکز مداری

خروج از مرکز مداری[۱] (به انگلیسی:Orbital eccentricity) پارامتریاست که توسط آن مقدار تفاوت مدار یک جرم به دور جرمی دیگر از نظر انحراف از یک دایرهٔ کامل بودن را تعیین میکند. مقدار صفر این پارامتر دایرهٔ کامل بودن یک مدار را نشان میدهد، مقادیر بین صفر و ۱ یک مدار بیضی شکل، و مقدار ۱ نمایانگر یک مدار سهموی فرار است و همچنین مقادیر بیشتر از ۱ یک مدار هذلولی است.
در مکانیک سماوی و طبق قانون اول کپلر مدار سیارات دایره نیست و بیضی است که خورشید به عنوان عامل گرانشی در یکی از کانونهای آن قرار گرفته؛ برای تمایز مقاطع مخروطی از یکدیگر از کمیتی استفاده میشود که به آن خروج از مرکز (انگلیسی: eccentricity) میگویند که با علامت () نشان داده میشود:
محاسبه خروج از مرکز مداری[ویرایش]
خروج از مرکز را میتوان از رابطه زیر به دست آورد:
که:
- خروج از مرکز برداری است.
برای مدارها میتوان از فرمول زیر و با استفاده از فواصل اوج و حضیض مداری:
که:
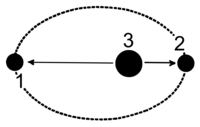
البته دو کمیت اخیر را نباید با نیم محور کوچک[۴] و نیممحور بزرگ[۵] بیضی اشتباه گرفت که نسبت به مرکز بیضی تعریف میشوند، حال آنکه نقاط اوج و حضیض مداری نسبت به کانون بیضی یا محل قرارگیری تقریبی خورشید تعریف میشوند[۶] دراین خصوص لطفاً به شکل مقابل مراجعه کنید. البته میتوان خروج از مرکز هر بیضی را هم با کمک این کمیتها و روابط زیر محاسبه کرد:
که در آن نیممحور بزرگ، نیممحور کوچک و فاصلهٔ هر کانون بیضی از مرکز بیضی است. روابط زیر ارتباط بین فواصل اوج و حضیض مداری و اندازهٔ نیم محور بزرگ را در بیضی نشان میدهند:
محاسبه مدار با کمک خروج از مرکز[ویرایش]

رابطه زیر نشان میدهد که چگونه با در دست داشتن خروج ار مرکز مداری میتوان مسیر مدار هر سیاره را مشخص کرد:
این رابطه با توجه به توضیحی که در بخش قبل داده شد میتواند بسته به مقدار خروج از مرکز مدارهایی به شکل یک مقطع مخروطی را توصیف کند، در این رابطه پارامتر f زاویهٔ موسوم به ناهنجار حقیقی[۷] که رأس آن کانون یا محل قرارگیری جرم مرکزی است و دو انتهای آن بین نقطهٔ حضیض مداری[۸] و نقطهای از مدار است که سیاره (ماهواره) در آنجا قرار میگیرد. (شکل مقابل)
کمیتهای فیزیکی و شکل مدار[ویرایش]
در مکانیک مبتنی بر قوانین پایه نیوتن موسوم به مکانیک کلاسیک برای برهم کنش اجسام از طریق میدانهای پایستار نیرو مسیرهای مشخص و قابل پیشبینی محاسبه میشود. ازجمله مسائل مکانیک کلاسیک برهم کنش اجرام در میدانهای گرانشی است که به ویژه برای یک جرم مرکزی و ماهواره در حال گردش بدور آن به مسئلهٔ برهمکنش دو جسم معروف است و بسته به مجموع انرژیهای جنبشی و پتانسیل ذخیره شده در میدان گرانش برای سامانه دو جرم میتوان با کمک ریاضیات پیشرفته و علم حسابان مسیر مداری را به صورت یک مقطع مخروطی محاسبه کرد.
با توضیح بالا ارتباط بین خروج از مرکز به عنوان کمیت تعیینکننده شکل مداری و کمیتهای فیزیکی در رابطهٔ زیر توصیف میشود:
که در آن کمیتهای فیزیکی زیر بکار رفتهاند:
- مقدار انرژی ویژه مداری،[۹] مجموع کل انرژیهای جنبشی ویژه و پتانسیل ویژه برای هر واحد از جرم کاهش یافته[۱۰] است؛ جرم کاهش یافته برابر نصف میانگین همساز جرمهای سامانه است که مثلاً برای دو جرم و با محاسبه میشود.
- مقدار تکانه زاویهای نسبی ویژه[۱۱] به ازا واحد جرم کاهش یافتهاست و مثلاً برای دو جرم در یک سامانه به معنی مقدار تکانه زاویهای کل بر جرم کاهش یافتهاست؛ تکانه زاویهای هر جسم بستگی به مکان، جرم و سرعت آن دارد.
- برابر با پارامتر گرانشی استاندارد[۱۲] برای مجموع جرمهاست؛ مثلاً برای دو جرم و و ثابت گرانش معادل است، این کمیت در تعیین سرعت گریز برای یک سیاره هم بار دیگر ظاهر میشود و دارای معادله ابعادی است.
اکنون با توجه به اینکه برای هر سامانه دو جرمی مقدار تکانه زاویهای بدون گشتاور خارجی بنا بر اصل پایستگی تکانهٔ زاویهای ثابت میمامند، خروج از مرکز تنها پیرو انرژی ویژه مداریست و حالتهای زیر را میتوان پیشبینی کرد:
- انرژی ویژه مداری در اینصورت مدار دقیقاً یک دایره است؛ این حداقل انرژی لازم برای تشکیل یک مدار پایدار است.
- انرژی ویژه مداری در اینصورت مدار یک بیضی است، مانند قریب به اتفاق اجرام سامانه خورشیدی.
- انرژی ویژه مداری در اینصورت مدار یک سهمی است مشابه بعضی ستارگان دنباله دار.
- انرژی ویژه مداری در اینصورت اجسام روی مدار هذلولی بدون بازگشت از یکدیگر تا بینهایت دور میشوند؛ و در نهایت در حالتی که انرژی ویژه مداری کمتر از مربوط به انرژی ویژه مداری در وضعیت مدار دایره است اساساً هیچگونه مدار پایداری وجود نخواهد داشت؛ دو جرم قادر به گریز از یکدیگر نیستند و نیروی جاذبه موجب سقوط یکی روی دیگری را فراهم میآورد.
مثالها[ویرایش]
خروج از مرکز زمین[ویرایش]
خروج از مرکز زمین در حال حاضر ۰٬۰۱۶۷است که به علت اثرات گرانشی دیگر سیارات به ویژه مشتری بهطور گردشی تغییر میکند (به نموداری که بر اساس دادههای سال ۱۹۹۱ میلادی رسم شده در پانویس این مطلب نگاه کنید[۱۳]). تحقیقات جامع جدیدتری از رصدخانه جنوبی اروپا که در سال ۲۰۱۱ میلادی منتشر گردید،[۱۴] نشان میدهد که خروج از مرکز مدار زمین با دورهٔ گردش تقریبی ۴۱۳۰۰۰ سال بین ۰٬۰۰۰۰۵۵ تا ۰٬۰۶۷۹ همزمان با شکل مداری بسیار نزدیک به دایره تا کمی بیضی تغییر میکند. این پدیده همراه با دیگر پدیدههای مشابه آن تأثیراتی روی اقلیم زمین دارند که بنام چرخههای میلانکوویچ معروفند.
خروج از مرکز سیارات[ویرایش]
شبه سیارهٔ پلوتو که حد فاصل سیارات سامانه خورشیدی است خروج از مرکزی معادل ۰٫۲۴۹ دارد و سیارهٔ تیر که نزدیکترین سیاره به خورشید است، خروج از مرکزی معادل ۰٫۲۰۶ دارد. جدول زیر خروج از مرکز سیارات سامانه خورشیدی را نشان میدهد.
| تیر | ناهید | زمین | بهرام | هرمز | کیوان | اورانوس | نپتون |
|---|---|---|---|---|---|---|---|
| ۰٬۲۰۶ | ۰٬۰۰۶۸ | ۰٬۰۱۶۷ | ۰٬۰۹۳ | ۰٬۰۴۸ | ۰٬۰۵۴ | ۰٬۰۴۷ | ۰٬۰۰۹ |
ماه هم خروج از مرکز ۰٫۰۵۵۴ دارد. کمترین خروج از مرکز در سامانه خورشیدی برای تریتون قمر نپتون معادل صفراست، یعنی مدار آن با تقریب بسیار خوبی[۱۶] یک دایرهٔ کامل را بدور نپتون میزند؛ البته چند قمر دیگر کیوان مانند پان هم دارای مداری تقریباً دایرهای هستند.[۱۷]
خروج از مرکز اجرام دیگر سامانه خورشیدی[ویرایش]
برای بیش از ۶۴۵۰۰۰ سیارک شناخته شده در کمربند سیارکی موسوم به کمربند اصلی که مدار گردش آنها بین مریخ و مشتری است، مقدار خروج از مرکز بهطور متوسط ۰٬۱۳۵ است.[۱۸] در میان بیش از ۴۶۰۰ ستارهٔ دنباله دار شناخته شده تا کنون لااقل حدود ۲۳۰ تا دارای خروج از مرکزی کمتر یا معادل با ۰٬۵ هستند و در بین آنها ستاره دنبالهدار معروف هالی که هر ۷۶ سال یکبار از نزدیک زمین عبور میکند، خروج از مرکزی معادل ۰٬۱۴۴ دارد.
پانویس[ویرایش]
- ↑ «خروج از مرکز» [هوافضا] همارزِ «eccentricity»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر یازدهم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۶۰۰-۶۱۴۳-۴۵-۳ (ذیل سرواژهٔ خروج از مرکز)
- ↑ apoapsis
- ↑ periapsis
- ↑ semi-minor axis
- ↑ semi-major axis
- ↑ دقیقتر این نقطه گرانیگاه سامانه سیاره-خورشید است
- ↑ true anomaly
- ↑ perihelion
- ↑ specific orbital energy
- ↑ reduced mass
- ↑ specific relative angular momentum
- ↑ standard gravitational parameter
- ↑ «نمودار تغییرات خروج از مرکز زمین دادهها از ۱۹۹۱ میلادی». بایگانیشده از اصلی در ۶ ژانویه ۲۰۱۸. دریافتشده در ۶ اوت ۲۰۰۸.
- ↑ a new orbital solution for the long-term motion
- ↑ «دادهها از ولفرام آلفا». بایگانیشده از اصلی در ۳۱ ژانویه ۲۰۱۶. دریافتشده در ۸ ژانویه ۲۰۱۵.
- ↑ خروج از مرکز دقیقتر ۰٬۰۰۰۰۱۶
- ↑ اطلاعات جامع تر در این خصوص
- ↑ «ماه نوامبر سال ۲۰۱۴ میلادی». بایگانیشده از اصلی در ۸ مه ۲۰۱۳. دریافتشده در ۹ ژانویه ۲۰۱۵.
منابع[ویرایش]
- Prussing, John E.، and Bruce A. Conway. Orbital Mechanicsc. New York: Oxford University Press، ۱۹۹۳.
پیوند به بیرون[ویرایش]
- World of Physics: Eccentricity
- The NOAA page on Climate Forcing Data includes (calculated) data from Berger (۱۹۷۸)، Berger and Loutre (1991)[پیوند مرده] and Laskar et al. (2004) on Earth orbital variations, including eccentricity, over the last 50 million years and for the coming 20 million years
- The orbital simulations by Varadi, Ghil and Runnegar (2003) provide another, slightly different series for Earth orbital eccentricity, and also a series for orbital inclination



































