سری فوریه
| تبدیل فوریه |
|---|

|
| تبدیل فوریه پیوسته |
| سری فوریه |
| تبدیل فوریه گسسته |
| تبدیل فوریه گسستهزمان |
سری فوریه بسطی است که هر تابع متناوب را به صورت حاصل جمع تعدادی نامتناهی از توابع نوسانی ساده (سینوسی، کسینوسی یا تابع نمایی مختلط) بیان میکند. این تابع به نام ریاضیدان بزرگ فرانسوی، ژوزف فوریه نامگذاری شدهاست. با بسط هر تابع به صورت سری فوریه، مولفههای بسامدی آن تابع به دست میآید.
پیش گفتار[ویرایش]
توابع مورد استفاده در مهندسی و توابع نمایانگر سیگنالها معمولاً توابعی از زمان هستند یا به عبارت دیگر توابعی که در میدان زمان تعریف شدهاند. برای حل بسیاری از مسائل بهتر است که تابع در دامنه فرکانس تعریف شده باشد؛ زیرا این دامنه ویژگیهایی دارد که به راحتی محاسبات میانجامد.
فرض کنید که تابعی به شکل زیر تعریف شدهاست:
که در آن یک عدد صحیح مثبت، دامنه، بسامد و فاز توابع کسینوسی میباشد. قابل مشاهده است که با در دست داشتن بسامدها ، دامنهها و فازها تابع بهطور کامل قابل تعریف است. توجه شود که بر اساس گفتههای بالا تابع مستقل از زمان قابل تعریف است.
نمایشهای مختلف سری فوریه[ویرایش]
نمایش مثلثاتی[ویرایش]
اگر یک تابع متناوب با دوره تناوب باشد (یا به عبارتی: ) آنگاه این تابع را میتوان به صورت زیر نوشت:
که در آن هارمونیک nام سری فوریه با رادیان بوده و ضرایب ، و را میتوان از فرمولهای اویلر بدست آورد.
فوریه بر این باور بود که هرگونه تابع متناوب را میتوان به صورت جمعی از توابع سینوسی نوشت. این مطلب درست نیست. شرایط لازم برای هر تابع متناوب برای اینکه به صورت سری فوریه نوشته شود به صورت زیر است:
- تابع در هر دورهٔ تناوبی انتگرال پذیر باشد:
- تابع فقط شمار محدودی بیشینه و کمینه داشته باشد.
- تابع فقط شمار محدودی ناپیوستگی داشته باشد.
نمایش مختلط[ویرایش]
سری فوریه میتواند به صورت زیر نیز نوشته شود:
و در اینجا:
این رابطه با کمک فرمول اویلر قابل گسترش به صورت زیر است:
اگر این رابطه را بهطور مستقیم با نمایش مثلثی مقایسه کنیم مشاهده میشود که به طریق زیر نیز قابل محاسبه است:
نمایش کسینوس-با-فاز[ویرایش]
نمایش زیر که در واقع شکل ویژهای از نمایش مثلثی میباشد، نمایش کسینوس-با-فاز نام دارد. از این نمایش در رسم طیف خطی (به انگلیسی: line spectra) استفاده میشود.
محاسبه ضرایب فوریه[ویرایش]
نمایش مثلثی[ویرایش]
نمایش مثلثی بالا را در نظر بگیرید. همانطور که گفته شد دوره تناوب و هارمونی nام تابع میباشد. در تبدیل فوریه سه ضریب و و ضریب ثابت مطرح است. ضریبها با استفاده از روابط زیر قابل محاسبه هستند.
بازه [-] یا در کل بازههایی که طول آنها است از مهمترین بازههایی است که درمحاسبه ضرایب استفاده میشود. بدین ترتیب پس ضرایب عبارتند از:
همگرایی[ویرایش]
-
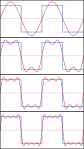
چهار مجموع جزئی اول سری فوریه برای یک موج مربعی
در کاربردهای مهندسی، بهطور کلی فرض میشود که سریهای فوریه تقریباً در همه جا همگرا شوند (استثنائاتی در ناپیوستگیهای گسسته وجود دارد) زیرا عملکردهایی که در مهندسی مشاهده میشوند رفتار بهتری نسبت به توابعی دارند که ریاضیدانان میتوانند به عنوان نمونههای متضاد این فرض ارائه دهند. بهطور خاص، اگر پیوسته باشد و مشتق (که ممکن است در همه جا وجود نداشته باشد) مربع انتگرال دار است، پس سریهای فوریه بهطور کامل و یکنواخت به همگرا میشوند.[۱]
-
چهار جمع جزئی (سری فوریه) با طول ۱ ، ۲ ، ۳ و ۴ جمله ای، که نشان میدهد چگونه تقریب با یک موج مربعی با افزایش تعداد جملهها بهبود مییابد.
-
چهار مجموع جزئی (سری فوریه) با طول ۱ ، ۲ ، ۳ و ۴ جمله ای، که نشان میدهد چگونه تقریب با یک موج دندانه اره ای با افزایش تعداد جملهها بهبود مییابد.
-
نمونه ای از همگرایی به یک تابع نسبتاً دلخواه. به شکلگیری "طنین" (پدیده گیبس) در انتقال به بخشهای عمودی توجه کنید.
جستارهای وابسته[ویرایش]
منابع[ویرایش]
- ↑ Tolstov, Georgi P. (1976). Fourier Series. Courier-Dover. ISBN 0-486-63317-9.
کتابشناسی[ویرایش]
- Yitzhak Katznelson, An introduction to harmonic analysis, Second corrected edition. Dover Publications, Inc. , New York, 1976. ISBN 0-486-63331-4
- Felix Klein, Development of mathematics in the 19th century. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen uber die Entwicklung der Matematik im 19 Jahrhundert, Springer, Berlin, 1928.
- Walter Rudin, Principles of mathematical analysis, Third edition. McGraw-Hill, Inc. , New York, 1976. ISBN 0-07-054235-X
- Kamen, Edward W.; Heck, Bonnie S. (2007). Signals And Systems. Prentice Hall. ISBN 0-13-168737-9.












![{\displaystyle f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(\omega _{n}t)+b_{n}\sin(\omega _{n}t)]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/667370577e20c5f28121d05e55cf7197b6a2016e)