لگاریتم

لُگاریتم[۱] (به انگلیسی: Logarithm) یک عدد در یک پایه، برابر با توانی از پایهاست که آن عدد را میدهد. برای نمونه لگاریتم ۱۰۰۰ در پایهٔ ۱۰، برابر با ۳ است. چون ۱۰ × ۱۰ × ۱۰ = ۱۰۰۰ یا به بیان کلیتر اگر x = by باشد آنگاه لگاریتم x در پایهٔ b برابر با y خواهد بود و به زبان ریاضی آن را به صورت نمایش میدهیم. مانند:
لگاریتم نخستین بار از سوی جان نپر در اوایل سده ۱۷ میلادی به عنوان وسیلهای برای آسانتر کردن محاسبات، معرفی شد؛ که به سرعت از سوی دانشمندان و مهندسان پذیرفته شد و برای آسانتر کردن و سریعتر کردن محاسبه جدولهای لگاریتم اعشاری و خطکشهای لغزنده ایجاد شدند و مورد استفاده قرار گرفتند. تمامی این ابزارها بر پایهٔ این مفهوم که «لگاریتم حاصل ضرب برابر است با مجموع لگاریتمها»، ساخته شده بودند:
مفهوم امروزی لگاریتم از تلاشهای لئونارد اویلر در قرن ۱۸ گرفته شدهاست؛ او توانست مفهوم لگاریتم را با مفهوم تابع نمایی پیوند دهد.
لگاریتم در پایهٔ ۱۰ را لگاریتم اعشاری مینامند که کاربرد بسیار زیادی در مهندسی دارد. لگاریتم در مبنای ثابت e یا عدد نپر ≈ ۲٫۷۱۸ را لگاریتم طبیعی مینامند. این لگاریتم در ریاضیات محض به ویژه حساب دیفرانسیل و انتگرال بسیار کاربرد دارد. لگاریتم دو دویی نیز در مبنای ۲ نوشته میشود و کاربرد زیادی در علوم رایانه دارد.
به کمک مقیاس لگاریتمی، میتوان اندازههای بسیار بزرگ را در ابعاد بسیار کوچکتری نشان داد برای نمونه دسیبل یکایی لگاریتمی است که برای نشان دادن فشار صدا و نسبت ولتاژ کاربرد دارد. در شیمی نیز پ هاش که معیاری برای نشان دادن میزان اسیدی بودن مایعات است در مقیاس لگاریتمی بیان میشود. همچنین لگاریتم در نظریهٔ پیچیدگی محاسباتی و در برخی شکلهای هندسی مانند برخالها کاربرد دارد. از دیگر کاربردهای آن میتوان به فاصله در موسیقی و رابطههای شمارش اعداد اول اشاره کردهمچنین در محاسبه زمان اجرای الگوریتمهای برنامههای کامپیوتری استفاده میشود.
تابع توان وارون تابع لگاریتم است و لگاریتم مختلط، تابع وارون تابع نمایی به کار رفته در اعداد مختلط است. لگاریتم گسسته نیز در رمزنگاری کلید عمومی استفاده میشود.
انگیزهٔ اولیه و تعریف[ویرایش]
انگیزهٔ ساخت لگاریتم، داشتن وارون تابع توان بودهاست. برای نمونه، توان سوم ۲، ۸ است چون ۸ = ۲ × ۲ × ۲ = ۲۳ پس لگاریتم ۸ در پایهٔ ۲، ۳ میشود.
به توان رساندن[ویرایش]
توان سوم عددی مانند b برابر است با ۳ بار ضرب b در خودش. حال اگر b به توان یک عدد طبیعی مانند n برسد به معنی n بار ضرب کردن b در خودش است که به صورت زیر نمایش میدهیم
در صورتی که n عدد طبیعی نباشد، آنگاه bn جواب دیگری خواهد داشت. مانند ۱- که b-۱ برابر معکوس b است. برای جزئیات بیشتر، شامل فرمول bm + n = bm · bn توان را ببینید[۲] یا یک رساله مقدماتی.
تعریف[ویرایش]
لگاریتم عددی مانند y در پایهٔ b عبارت است از یافتن عددی که اگر b به توان آن عدد برسد برابر با y شود. به عبارت دیگر جواب x معادلهٔ زیر برابر با لگاریتم y در پایهٔ b خواهد بود.[۳]
پایهٔ b باید یک عدد حقیقی مثبت و نامساوی ۱ باشد و y نیز باید یک عدد مثبت باشد.[۳]
چند نمونه[ویرایش]
- نمونهٔ یکم
برای نمونه ۴ = (۱۶) log۲ چون ۱۶ = ۲ × ۲ × ۲ × ۲ = ۲۴
- نمونهٔ دوم
برای توانهای منفی نیز لگاریتم معتبر است مانند:
چون
- نمونهٔ سوم
(۱۵۰) log۱۰ تقریباً برابر است با ۲٫۱۷۶ عددی میان ۲ و ۳ چون ۱۵۰ خود عددی است میان ۱۰۰ = ۱۰۲ و ۱۰۰۰ = ۱۰۳ همچنین در هر پایهای و چون به ترتیب: و است.
قوانین لگاریتم[ویرایش]
رابطههای مختلفی به عنوان قوانین لگاریتم وجود دارند که میتوانند میان فرمولهای لگاریتمی رابطه برقرار کنند.
ضرب، تقسیم، توان، ریشه[ویرایش]
لگاریتم حاصل ضرب چند عدد برابر است با مجموع لگاریتمهای تک تک آن عددها. لگاریتم نسبت دو عدد (تقسیم) برابر است با تفاضل لگاریتم آن دو عدد. لگاریتم توان p ام یک عدد برابر است با p برابر لگاریتم آن عدد. لگاریتم ریشهٔ p ام یک عدد برابر است با لگاریتم آن عدد تقسیم بر p. جدول زیر قوانین لگاریتم را همراه با یک نمونه نشان دادهاست:
| رابطه | نمونه | |
|---|---|---|
| ضرب | ||
| تقسیم | ||
| توان | ||
| ریشه |
تغییر پایه[ویرایش]
میتوان را به صورت غیرمستقیم با گرفتن لگاریتم x و b در یک پایهٔ دلخواه مانند k بدست آورد، به این ترتیب که:
بیشتر ماشین حسابهایی که در دسترس اند لگاریتم را تنها در مبنای ۱۰ و عدد نپر[۴] محاسبه میکنند و لگاریتم در پایههای دیگر را به کمک رابطهٔ بالا محاسبه میکنند::
همچنین اگر عددی مانند x و مقدار لگاریتم آن را در یک مبنای نامشخص b داشته باشیم حال میتوان مبنای نامشخص b را به ترتیب زیر محاسبه کرد:
۳ ویژگی مهم لگاریتم[ویرایش]
پایههای ویژه[ویرایش]
پایههای ویژهٔ لگاریتم عبارتند از ۱۰، ۲ و عدد e (عدد گنگی تقریباً برابر با ۲٫۷۱۸۲۸) در آنالیز ریاضی لگاریتم در پایهٔ عدد e بسیار کاربرد دارد، لگاریتم در پایهٔ ۱۰ را میتوان بوسیلهٔ ماشین حسابهای دستی که در اختیار است به آسانی محاسبه کرد:[۵]
لگاریتم در پایهٔ ۱۰ را میتوان به آسانی با شمردن تعداد رقمهای یک عدد بدست آورد. برای نمونه (۱۴۳۰) log۱۰ تقریباً برابر است با ۳٫۱۵ چون ۱۴۳۰ چهار رقم دارد پس لگاریتم آن در پایهٔ ۱۰ باید عددی میان ۳ و ۴ باشد. لگاریتم در پایهٔ ۲ در علوم رایانه مورد استفاده قرار میگیرد چون در آن از دستگاه اعداد دودویی استفاده میشود.
جدولی که در ادامه قرار داده شدهاست علامتهایی که برای نشان دادن تابع لگاریتم کاربرد دارند و جایی که هر نوع لگاریتم مورد استفاده قرار میگیرد را نشان دادهاست. در بسیاری موارد اگر بتوان از روی نوشته تشخیص داد تنها از نماد لگاریتم استفاده میکنند و از نوشتن پایهٔ آن خودداری میکنند. در جدول زیر نمادی ستون «نماد ISO» مربوط به پیشنهادی است که از سوی سازمان بینالمللی استانداردسازی[۶] داده شدهاست. (ISO ۳۱–۱۱)
| پایهٔ b | نام گونهٔ لگاریتم | ISO نماد در | دیگر نمادها | کاربرد |
|---|---|---|---|---|
| ۲ | لگاریتم دودویی یا لگاریتم باینری | lb(x)[۷] | ld(x), log(x) (در علوم رایانه)، lg(x) |
علوم رایانه: این لگاریتم پیشفرض در پایه ۲ بوده و در طراحی نرمافزار بهویژه بانکهای اطلاعاتی مانند محاسبات آیپی۴ و ۶ و غیره کاربردهای بسیاری دارد، همچنین سختافزار، نظریهٔ اطلاعات |
| e | لگاریتم طبیعی | ln(x)[nb ۱][۸]
The notation was invented by Irving Stringham, a mathematician.[۹][۱۰] |
log(x) (در ریاضی و بسیاری از زبانهای برنامهنویسی[nb ۲]) |
آنالیز ریاضی، فیزیک، شیمی آمار، علم اقتصاد، و بعضی از زمینههای مهندسی |
| ۱۰ | لگاریتم اعشاری | lg(x) | log(x) (در مهندسی، زیستشناسی، اخترشناسی), |
در زمینههای گوناگون مهندسی (مانند دسیبل)، تهیه جدول لگاریتم و ماشین حسابهای مهندسی |
پیشینه[ویرایش]
پیشینیان[ویرایش]
ویراسنا، ریاضیدان هندی از کسانی بود که با مفهومی به نام ardhaccheda کار کرد. ardhaccheda یعنی تعداد دفعاتی که میتوان ۲n را نصف کرد. برای نمونه برای توانهای دقیق ۲ این کار برابر با لگاریتم گرفتن در مبنای ۲ بود؛ وی همچنین لگاریتم در پایهٔ دیگر اعداد صحیح مانند لگاریتم در پایهٔ ۳ (trakacheda) و در پایهٔ ۴ (caturthacheda) را نیز معرفی کرد.[۱۱][۱۲] مایکل استیفل در سال ۱۵۴۴ میلادی در نورنبرگ Arithmetica integra را منتشر کرد، در این نوشته جدولی از اعداد صحیح و توانهای ۲ داده شده بود، این جدول به عنوان نسخهٔ اولیهٔ جدول لگاریتم شمرده میشود.[۱۳][۱۴]
از نپر تا اویلر[ویرایش]

روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio (توصیفی بر قانون شگفتانگیز لگاریتم) ارائه شد.[۱۵] همچنین ژو بورجی (به فرانسوی: Joost Bürgi) نیز جداگانه روش لگاریتمگیری را پیدا کرده بود اما آن را شش سال پس از نپر منتشر کرد.[۱۶]
نپر، با استفاده از روش تقسیمهای متوالی توانسته بود عبارت را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریباً برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند:
نپر ابتدا نام «عدد ساختگی» را بر L نهاد ولی پس از مدتی واژهٔ «لگاریتم» logarithm را معرفی کرد و آن را بر عددی گذاشت که نمایندهٔ یک نسبت است: واژهٔ λόγος برابر logos به معنی «نسبت» است و واژهٔ ἀριθμός برابر arithmos به معنی «عدد» است. بوسیلهٔ عبارت زیر میتوان مفهوم پیشین لگاریتم را با مفهوم امروزی لگاریتم طبیعی مرتبط کرد:[۱۷][۱۸]
با تقریب خوبی داریم:
این دستآورد خیلی زود مورد تحسین گستردهٔ دیگران قرار گرفت، به همین دلیل با تلاش دانشمندانی چون بوناونتورا کاوالیری (Bonaventura Cavalieri) از ایتالیا، ادموند ونگت (Edmund Wingate) از فرانسه، زو فنگزوئو (Xue Fengzuo) از چین و… مفهوم لگاریتم همه جا فراگیر شد.[۱۹]
در سال ۱۶۴۷ گرگوآر دو سن-ونسان توانست مفهوم لگاریتم را با یک چهارم هذلولی مرتبط کند، با فرض آنکه سطح زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند:
لگاریتم طبیعی اولین بار از سوی نیکولاس مرکاتور در مقالهٔ Logarithmotechnia که در سال ۱۶۶۸ منتشر کرد، توضیح داده شد.[۲۰] البته پیش از او جان اسپیدل که یک معلم ریاضی بود در سال ۱۶۱۹ جدولی از لگاریتم طبیعی را گردآوری کرده بود.[۲۱] در حدود سال ۱۷۳۰ لئونارد اویلر تابع نمایی و لگاریتم طبیعی را به گونهٔ زیر تعریف کرد:
همچنین اویلر نشان داد که این دو تابع وارون یکدیگرند.[۲۲][۲۳][۲۴]
جدول لگاریتم، خطکش لغزان و کاربردها در گذشته[ویرایش]

با سادهسازی محاسبات پیچیده، از لگاریتم میتوان در دانش پیشرفته مانند اخترشناسی، نقشهبرداری، هوانوردی و… کمک گرفت. پیر سیمون لاپلاس دربارهٔ لگاریتم گفتهاست:
وسیلهای ستودنی است که به کمک آن کار چند ماه به چند روز کاهش مییابد، عمر اخترشناسان را دو برابر میکند و از خطاهای کوچک میگذرد و از جملههای طولانی و جدانشدنی ریاضی بیزار است.
وسیلهٔ کلیدی که پیش از در دسترس قرار گرفتن ماشین حساب و رایانه برای محاسبهٔ لگاریتم از آن استفاده میشد و بوسیلهٔ آن بود که ارزش لگاریتم روشن شد، جدول لگاریتم بود.[۲۶] چنین جدولی برای اولین بار بوسیلهٔ هنری بریگز در سال ۱۶۱۷ بلافاصله پس از ابتکار نپر ایجاد شد. پس از آن جدولهای وسیع تر و دقیق تری نوشته شد. در این جدولها مقدار و برای هر عدد x در یک بازهٔ مشخص با دقت مشخص و برای پایههای مشخص (معمولاً پایهٔ ۱۰) نوشته شده بود. برای نمونه در اولین جدول بریگز، لگاریتم طبیعی اعداد صحیح میان ۱ تا ۱۰۰۰ با دقت ۸ رقم اعشار نوشته شده بود. از آنجایی که تابع وارون است به آن پادلگاریتم (به انگلیسی: antilogarithm) میگویند.[۲۷] لگاریتم ضرب و تقسیم دو عدد را همیشه به صورت جمع و تفاضل لگاریتمهای آنها نشان میدادند. ضرب و تقسیم عبارت داخل لگاریتم را میتوان بوسیلهٔ تابع پادلگاریتم یا خود جدول بدست آورد:
و
زمانی که رایانه در دسترس نیست، جستجوی جدولهای لگاریتم و استفاده از جمع و تفریق لگاریتمها بسیار آسانتر از روشهای سادهسازی مانند روش Prosthaphaeresis است. روش یاد شده بر پایهٔ اتحادهای مثلثاتی است. شمارش توانها و ریشههای اعداد به انجام عمل ضرب و تقسیم و جستجوی جدول به ترتیب زیر کاهش یافتهاست:
و
در بسیاری از جدولها برای محاسبهٔ لگاریتم بخش اعشاری و بخش صحیح را از یکدیگر جدا میکردند[۲۸] مانند نمونهٔ زیر:
وسیلهٔ دیگری که برای شمارش لگاریتم کاربرد داشت، خطکش لغزان بود.

مدت کوتاهی پس از کشف لگاریتم از سوی نپر، ادموند گونتر خطکشی (معیاری) برای بدست آوردن لگاریتم ایجاد کرد که لغزان نبود و به کمک آن میشد لگاریتمها را بدست آورد. پس از او ویلیام اوترد روش پیشرفتهتری را پیشنهاد کرد که دارای یک جفت لگاریتمهایی بود که در دو لبهٔ خطکش قرار داده شده بود و با لغزاندن دو لبهٔ خطکش میشد لگاریتم مورد نظر را به دست آورد. تا سال ۱۹۷۰ این خطکش وسیلهٔ محاسبهگر مهمی برای مهندسان و دانشمندان بود؛ چون به کمک آن، با دقت کافی و بسیار سریع تر از جدولها، میشد لگاریتم عدد را به دست آورد.[۲۲]
ویژگیهای ریاضی[ویرایش]
مطالعهٔ بیشتر در بحث لگاریتم نیازمند مطرح کردن مفهوم تابع است. یک تابع مانند یک قانون عمل میکند که اگر یک عدد ورودی داشته باشد، در مقابل یک خروجی تولید میکند.[۲۹] مانند تابع توان x ام عدد حقیقی b که به صورت زیر نوشته میشود:
تابع لگاریتم[ویرایش]
برای درک تابع لگاریتم باید نشان داد که معادلهٔ زیر:
دارای راه حل و جواب یکتای x است به شرطی که y بزرگتر از صفر باشد و b بزرگتر از صفر و نامساوی ۱ باشد. برای اثبات این مطلب باید از قضیهٔ مقدار میانی در حساب دیفرانسیل و انتگرال استفاده کرد. این قضیه نشان میدهد که اگر تابع پیوستهای دو مقدار m و n را تولید کند، هر مقداری میان این دو عدد را نیز به دلیل پیوستگی میتواند تولید کند. یک تابع را زمانی پیوسته میدانیم که در هیچ نقطهای ار آن «پرش» نداشته باشیم و بدون بلندکردن قلم از روی کاغذ بتوانیم خم آن را بکشیم. میتوان نشان داد که در تابع نیز همین ویژگی وجود دارد، برای هر y> ۰ که میان دو مقدار و به ازای x۰ و x۱ قرار داشته باشد طبق قضیهٔ مقدار میانی میتوان یک x پیدا کرد که باشد؛ بنابراین برای معادلهٔ یک جواب پیدا شد که میتوان گفت تنها جواب این معادلهاست چون تابع f برای b> ۱ اکیداً صعودی و برای b میان ۰ و ۱ اکیداً نزولی است.[۳۰]
جواب پیدا شده برای این معادله همان لگاریتم y در پایهٔ b است.
قرینه تابع لگاریتمی[ویرایش]
اگر قرینه تابع برابر با باشد نسبت به محور yها قرینه هم هستند.
اگر قرینه تابع برابر با باشد نسبت به محور xها قرینه هم هستند.
تابع وارون[ویرایش]

لگاریتم تابع توانی برای هر عدد x به صورت زیر نوشته میشود:
اگر پایهٔ توان و لگاریتم هر دو b باشد جواب نهایی رابطهٔ بالا قطعاً خود x خواهد بود. همچنین اگر عدد مثبت y را داشته باشیم، رابطهٔ زیر نیز برقرار خواهد بود:
بنابراین در هر دو صورت میتوان دو تابع توانی و لگاریتم را ترکیب کرد و دوباره به مقدار اولیه رسید. پس لگاریتم در پایهٔ b تابع وارون f(x) = bx است.[۳۱]
دو تابع وارون همواره با یکدیگر ارتباط دارند به این ترتیب که خمهای آنها قرینهٔ یکدیگر نسبت به خط y = x است (مانند شکل) همچنین در تابع اگر x به سمت مثبت بینهایت برود مقدار تابع لگاریتم نیز به ازای b> ۱ به سمت مثبت بینهایت خواهد رفت در این حال میگوییم تابع اکیداً صعودی است. به ازای b <۱ اگر x به سمت مثبت بینهایت رود، مقدار تابع به سمت منفی بینهایت میرود. وقتی x به سمت صفر میرود مقدار تابع برای b> ۱ به سمت منفی بینهایت میرود و برای b <۱ به سمت مثبت بینهایت میرود.
مشتق و پادمشتق[ویرایش]

ویژگیهای ریاضی یک تابع را میتوان در تابع وارون آن نیز جستجو کرد.[۳۲] پس چون f(x) = bx یک تابع پیوسته و مشتقپذیر است، میتوان نتیجه گرفت که نیز همین ویژگی را دارد. یک تابع پیوسته مشتقپذیر است اگر هیچ نقطهٔ تیزی (نقطهٔ شکستگی) در آن وجود نداشته باشد. از آنجایی که میتوان نشان داد که مشتق برابر با است، با استفاده از ویژگیهای تابع نمایی و قاعدهٔ زنجیری به این نتیجه میرسیم که مشتق برابر است با:[۳۰][۳۳]
که این شیب خط مماس در نقطهٔ x بر خم است که برابر است با . همچنین مشتق برابر با است که به این معنی است که پادمشتق همان است. اگر به جای x حالت کلی را در نظر بگیریم، در این حالت خواهیم داشت:
گاهی برای بدست آوردن مشتق تابع f از استفاده میکنند که به این کار مشتقگیری لگاریتمی میگویند.[۳۴] پادمشتق لگاریتم طبیعی برابر است با:[۳۵]
رابطههای مرتبط با دیگر پایههای لگاریتم با استفاده از فرمول لگاریتم طبیعی که در بالا گفته شد بدست میآید.[۳۶]
بیان انتگرالی لگاریتم طبیعی[ویرایش]
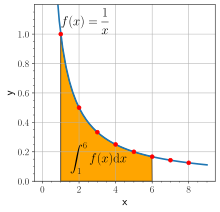
لگاریتم طبیعی t برابر است با انتگرال از ۱ تا t:
به عبارت دیگر برابر است با سطح میان محور xها و نمودار تابع از ۱ = x تا (شکل مقابل). این مطلب، از نتایج قضیهٔ اساسی حسابان و اینکه مشتق ، است، میباشد. عبارت سمت راست این رابطه را میتوان به عنوان تعریفی برای لگاریتم طبیعی در نظر گرفت. فرمولهای ضرب و توان لگاریتمی را میتوان از این تعریف نتیجه گرفت.[۳۷] برای نمونه را میتوان به صورت زیر نتیجه گرفت:
بخش نخست تساوی انتگرال را به دو بخش جدا میشکند و بخش دوم تساوی، تغییر متغیر میدهد (). در نگارهای که در پایین نشان داده شدهاست، سطح زیر منحنی که برابر با انتگرال بالا است به دو ناحیهٔ آبی و زرد تقسیم شدهاست. در قسمت آبی همانطور که خم در جهت x کشیده شده (t برابر شده) به همان اندازه هم در جهت عمودی دچار جمع شدگی شدهاست بنابراین سطح زیر منحنی سمت راست که انتگرال f(x) = ۱/x از ۱ تا u است با سطح زیر آن از t تا tu برابر است. پس روی شکل سمت چپ نشان داده شد که یا سطح زیر منحنی برابر است با مجموع و (سطح زرد و آبی)

رابطهٔ توان را نیز به همین ترتیب میتوان اثبات کرد:
در تساوی دوم تغییر متغیر را داریم.
مجموع وارونهای اعداد طبیعی:
که سری هارمونی نام دارد، به لگاریتم طبیعی بسیار نزدیک است: هرگاه n به سمت بینهایت برود، تفاضل زیر:
به عددی معروف به ثابت اویلر-مسکرونی، همگرا میشود. این ارتباط در تحلیل عملکرد الگوریتمهایی مانند مرتبسازی سریع کمک میکند.[۳۸]
محاسبه[ویرایش]
در بعضی موارد مانند ۳ = (۱۰۰۰) log۱۰ محاسبهٔ لگاریتم بسیار آسان است. در حالت کلی لگاریتم را به کمک سریهای توانی یا ابزارهای محاسباتی-هندسی یا به کمک بازیابی جدول لگاریتم که پیش از این محاسبه شده و دقت کافی دارد، محاسبه میکنند.[۳۹][۴۰] همچنین برای محاسبهٔ میتوان از الگوریتم لگاریتمهای دودویی که به صورت بازگشتی و بر پایهٔ مربعهای پشت هم از x عمل میکند استفاده کرد:
روش تقریبی نیوتن که یک روش تکرار شونده برای حل تقریبی معادلات است، میتواند برای بدست آوردن مقدار لگاریتم مفید باشد؛ چون تابع وارون لگاریتم، تابع نمایی با تقریب خوبی قابل محاسبهاست.[۴۱] در صورتی که تنها ابزار در دسترس ابزار جمع و اعداد پایهٔ دو باشد، میتوان با جستجو در میان جدول CORDIC یا «روش رقم به رقم» روشهای مناسبی برای محاسبهٔ لگاریتم پیدا کرد.[۴۲][۴۳]
سریهای توانی[ویرایش]
سری تیلور[ویرایش]
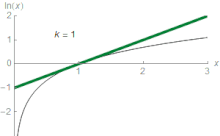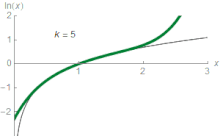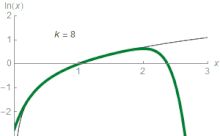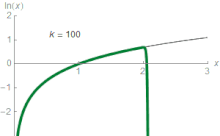
برای هر عدد حقیقی z که میان کوچکتر از ۲ و بزرگتر از صفر است رابطهٔ زیر برقرار است:[nb ۳][۴۴]
با استفاده از روابط زیر را میتوان دقیقتر بدست آورد:
برای نمونه، تقریب سوم به ازای z = ۱٫۵ نتیجه برابر با ۰٫۴۱۶۷ خواهد بود که تقریباً ۰٫۱۱ بیشتر از ۰٫۴۰۵۴۶۵ = (۱٫۵) ln است. در حساب دیفرانسیل غیر پیشرفته، را به عنوان حد این نوع سریها در نظر میگیرند؛ که به آن بسط تیلور لگاریتم طبیعی به ازای z = ۱ میگویند.
دیگر سریهای پرکاربرد[ویرایش]
سری دیگر برپایهٔ تابع وارون تانژانت هذلولوی (وارون تانژانت هیپربولیک) است، این سری برای اعداد مختلط z با بخش حقیقی[۴۴] مثبت است که به صورت زیر نوشته میشود:
با استفاده از مفهوم جمع (سیگما) میتوان این سری را به گونهٔ دیگری نوشت:
این سری از سری تیلور که در بالا گفته شد گرفته میشود ولی خیلی زودتر از تیلور همگرا میشود. به ویژه زمانی که z عددی نزدیک ۱ باشد. برای نمونه برای z = ۱٫۵ سه جملهٔ اول سری دوم با خطایی برابر با ۶-۱۰ × ۳ تقریباً میتوان گفت تقریباً برابر با (۱٫۵)ln است. اینکه به ازای zهای نزدیک به ۱ سری زودتر همگرا میشود را میتوان به کمک رابطهٔ زیر نشان داد:
فرض کنید تقریباً و رابطهٔ زیر را نیز داریم:
میتوان از دو سوی رابطهٔ بالا لگاریتم گرفت:
هرچه مقدار لگاریتم z دقیقتر باشد باید به صفر نزدیک تر باشد در نتیجه A به ۱ نزدیکتر است. مقدار A به کمک سریهای نمایی محاسبه میشود که این سریها، اگر y بزرگ نباشد، خیلی زود همگرا میگردند.
برای آسانتر کردن محاسبهٔ میتوان آن را به مقدارهای کوچکتر خُرد کرد به این ترتیب که بگوییم a × 10b = z و لگاریتم آن را به صورت بنویسیم.
از روش مشابهی میتوان استفاده کرد تا به کمک آن لگاریتم اعداد صحیح را بدست آورد:
اگر لگاریتم عدد بزرگ n معلوم باشد، میتوان لگاریتم n + ۱ را با همگرایی سریع سری بالا بدست آورد.
میانگین حسابی-هندسی[ویرایش]
با کمک میانگین حسابی-هندسی میتوان با دقت خوبی لگاریتم طبیعی عددی مانند x را بدست آورد. میزان تقریب آن برابر با است. این رابطه از سوی ریاضیدان آلمانی کارل فریدریش گاوس پیشنهاد شد.[۴۵][۴۶]
در اینجا M نماد میانگین حسابی-هندسی است که از تکرار محاسبهٔ میانگین حسابی و ریشهٔ دوم ضرب دو عدد (میانگین هندسی) بدست میآید. همچنین m از راه انتخابی مانند زیر بدست میآید:
هم میانگین حسابی-هندسی و هم ثابتهای π و (۲)ln به کمک سریهایی که زود همگرا میشوند قابل محاسبهاند.
کاربرد[ویرایش]

مفهوم لگاریتم کاربردهای زیادی در بیرون و درون دنیای ریاضی دارد. برخی از پیشامدهای لگاریتم در طبیعت، بیشتر به مفهوم نامتغیر مقیاس مرتبط است. برای نمونه هر خانهٔ پوستهٔ بدن آبزی ناتیلوس تقریباً رونوشتی از خانهٔ کناری آن است که با یک ضریب ثابت مقیاس یافتهاست و یک مارپیچ لگاریتمی را ساختهاست.[۴۷] قانون بنفورد در توزیع شمارگان (رقمها) را هم میتوان با مفهوم نامتغیر مقیاس توضیح داد.[۴۸] همچنین مفهوم لگاریتم به بحث خودهمانندی هم مرتبط است. برای نمونه پردازش لگاریتمی کمک میکند تا برای حل یک مسئله، نخست آن را به دو مسئلهٔ همانند کوچکتر بخش کنیم سپس جواب دو بخش را به هم پیوند دهیم.[۴۹] شکلهای هندسی خودهمانند که در آنها بخشهایی از شکل متناسب با سراسر آن است هم به لگاریتم وابستهاند. مقیاس لگاریتمی مقیاسی بسیار پرکاربردی برای بررسی کمّی تغییرات پدید آمده در مقدار اصلی است. افزون بر این چون تابع log(x) رشد بسیار کندی دارد به ویژه برای xهای بزرگ میتوان دادههای علمی در بازههای بزرگ را به خوبی فشرده کرد. همچنین پیش میآید که در بسیاری از فرمولهای علمی مانند معادلهٔ فنسک، معادلهٔ نرنست و… از ویژگیهای لگاریتم بهره برد.
مقیاس لگاریتمی[ویرایش]
کمیتهای علمی بیشتر به صورت لگاریتم کمیتهای دیگر ارائه میشوند به عبارت دیگر برای نشان دادن آنها از مقیاس لگاریتمی بهره برده میشود، برای نمونه دسیبل چنین است. برای نشان دادن تراز توان صداها در صداشناسی[۵۰] یا جذب نور در میدان طیفسنجی و نورشناسی یا در بیان نسبت سیگنال به نویز و توضیح میزان صداهای نامطلوب به سیگنالهای بامعنی به دسیبل نیاز است.[۵۱] همانند آنچه گفته شد، نسبت سیگنال بالایی به نویز برای ارزیابی کیفیت صدا یا فشردهسازی تصویر بسیار کاربرد دارد که در آن هم از لگاریتم بهره برده میشود.[۵۲]
موسیقی[ویرایش]
لگاریتم با مفهوم ارتفاع و فاصله در موسیقی هم مرتبط است. در سامانهٔ ارتفاعهایی که همهٔ جفت نتها، نسبت بسامد برابر دارند، نسبت بسامد تنها به فاصلهٔ میان دو ارتفاع بستگی دارد و نه به آن بسامد ویژه یا ارتفاع هر یک عدد نت. برای نمونه: نت لا بسامد ۴۴۰ هرتزی دارد و نت سی بمل نیز دارای بسامد ۴۶۶ هرتز است.
فاصله میان این دو نت یک نیم ارتفاع نام دارد. همچنان که میان نت سی بمل و نت سی با بسامد ۴۹۳ هرتز هم همینطور است. برپایهٔ آنچه گفته شد نسبت این بسامدها به صورت زیر است:
از این رو میتوان از لگاریتم برای توضیح فاصلهها بهره برد: یک فاصله در نیم-ارتفاع با گرفتن لگاریتم نسبت بسامد در پایهٔ ۲۱/۱۲ یا در پایهٔ ۲۱/۱۲۰۰ اندازهگیری میشود. پایه دوم برای توصیف دقیقتر به کار میرود چرا که از آن برای temperamentهای نامساوی بهره گرفته میشود.[۵۳]
| فاصله (دو ارتفاعی که همزمان نواخته میشوند) |
ارتفاع ۱/۱۲ |
نیم-ارتفاع |
سوم بزرگ میانه |
سوم بزرگ |
ارتفاع سگان |
هشتگان |
| نسبت بسامد r | ||||||
| شمارهٔ نیم-ارتفاعهای متناظر |
||||||
| تعداد سنتهای مرتبط |
نظریهٔ اعداد[ویرایش]
لگاریتم طبیعی ارتباط نزدیکی با شمارش اعداد اول دارد. این مطلب موضوعی مهم در نظریهٔ اعداد است. برای هر عدد صحیح x شمار عددهای اول کوچکتر یا مساوی x را با π(x) نمایش میدهند. نظریهٔ اعداد اول میگوید که π(x) تقریباً برابر است با:
با در نظر گرفتن این مطلب که برای xهایی که به بینهایت میرود نسبت π(x) به کسر بالایی به یک نزدیک میشود.[۵۴] از این مطلب میتوان نتیجه گرفت که احتمال اول بودن یک عدد دلخواه میان یک و x با وارون تعداد رقمهای دهدهی x متناسب است. یک برآورد خیلی بهتر π(x) با کمک انتگرال لگاریتمی زیر بدست میآید:
حدس ریمان یکی از کهنترین حدسهای ریاضی است که در مقایسهٔ π(x) و Li(x) کاربرد دارد.[۵۵] نظریهٔ اردوش-کاک به توضیح شمار عاملهای اول میپردازد که در آن از مفهوم لگاریتم طبیعی کمک گرفته شدهاست.
لگاریتم n فاکتوریل، n! = ۱ · ۲ ·... · n چنین است:
از این برای بدست آوردن تقریب استرلینگ، یک تقریب n! برای nهای بزرگ، استفاده میشود.[۵۶]
حالت کلی[ویرایش]
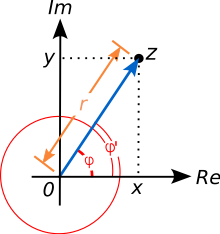
عدد مختلط a جواب معادلهٔ زیر، یک لگاریتم مختلط است.
z عددی مختلط است. یک عدد مختلط را به صورت z = x + iy نمایش میدهیم که x و y هر دو عددی حقیقی و i یکهٔ موهومی است. چنین عددی را میتوان با یک نقطه بر روی صفحهٔ مختلط نمایش داد (مانند روبرو). فرم قطبی نمایش دهندهٔ عدد ناصفر مختلط z است که قدر مطلق آن برابر است با فاصلهٔ r تا مبدأ مختصات و زاویهٔ میان خط گذرا از z و مبدأ با محور x زاویهٔ مربوط به این عدد مختلط است. قدر مطلق z همان r است که برابر است با:
چون φ' = φ + ۲π پس هم φ و هم 'φ هر دو زاویهٔ مربوط به zاند. تنها یک φ است که در رابطهٔ −π <φ صدق میکند که به آن آرگومان اصلی گفته میشود و به صورت Arg(z) نمایش داده میشود.[۵۷] گاهی هم به صورت ۰ ≤ Arg(z) <2π تعریف میشود.[۵۸]

با بهرهگیری از تابعهای مثلثاتی سینوس و کسینوس یا شکل نمایی اعداد مختلط به ترتیب به رابطههای زیر میرسیم، r و φ را بالاتر تعریف کردیم:[۵۹]
در آغاز معادلهای را بیان کردیم که در آن توان a ام e برابر با z میشد. با توجه به آنچه گفته شد، مقدار a برابر خواهد بود با:
در این رابطه، n هر عدد صحیحی میتواند باشد.
جستارهای وابسته[ویرایش]
یادداشتها[ویرایش]
- ↑ Some mathematicians disapprove of this notation. In his 1985 autobiography, پل ریچارد هالموس criticized what he considered the "childish ln notation," which he said no mathematician had ever used.
- ↑ برای نمونه زبان برنامهنویسی C، زبان برنامهنویسی جاوا، زبان برنامهنویسی هسکل و زبان برنامهنویسی بیسیک.
- ↑ The same series holds the principal value of the complex logarithm for complex numbers z satisfying |z − ۱| <1.
پانویس[ویرایش]
- ↑ «لگاریتم» [ریاضی] همارزِ «logarithm»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر اول. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۳۱-۱ (ذیل سرواژهٔ لگاریتم)
- ↑ Shirali, Shailesh (2002), A Primer on Logarithms, Hyderabad: Universities Press, ISBN 978-81-7371-414-6, esp. section 2
- ↑ ۳٫۰ ۳٫۱ Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8, chapter 1
- ↑ Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw Hill Financial, ISBN 978-0-07-005023-5, p. 21
- ↑ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, N.Y.: Barron's, ISBN 978-0-7641-1972-9, chapter 17, p. 275
- ↑ B. N. Taylor (1995), Guide for the Use of the International System of Units (SI), US Department of Commerce
- ↑ Gullberg, Jan (1997), Mathematics: from the birth of numbers., New York: W. W. Norton & Co, ISBN 978-0-393-04002-9
- ↑ Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96078-4
- ↑ Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, p. xiii
- ↑ Roy S. Freedman (2006), Introduction to Financial Technology, Amsterdam: Academic Press, p. 59, ISBN 978-0-12-370478-8
- ↑ Gupta, R. C. (2000), "History of Mathematics in India", in Hoiberg, Dale; Ramchandani (eds.), Students' Britannica India: Select essays, New Delhi: Popular Prakashan, p. 329
{{citation}}:|editor3-first=missing|editor3-last=(help) - ↑ Dr. Hiralal Jain, ed. (1996), THE SHATKHANDAGAMA OF PUSHPADANTA AND BHOOTABAL (3rd ed.), Solapur: Jain Samskriti Samrakshaka Sangha, archived from the original on 11 May 2011, retrieved 22 August 2011
{{citation}}: Unknown parameter|unused_data=ignored (help), part 3-4-5, book 4 - ↑ Bukhshtab, A.A.; Pechaev, V.I. (2001) [1994], "Arithmetic", Encyclopedia of Mathematics, EMS Press
- ↑ Vivian Shaw Groza and Susanne M. Shelley (1972), Precalculus mathematics, New York: Holt, Rinehart and Winston, p. 182, ISBN 978-0-03-077670-0
- ↑ Ernest William Hobson (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press
- ↑ Boyer 1991, Chapter 14, section "Jobst Bürgi"
- ↑ William Harrison De Puy (1893), The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint, vol. 17 (9th ed.), Werner Co., p. 179
- ↑ ایوز، آشنایی با تاریخ ریاضیات، ۶.
- ↑ Maor, Eli (2009), E: The Story of a Number, Princeton University Press, ISBN 978-0-691-14134-3, section 2
- ↑ J. J. O'Connor; E. F. Robertson (2001-09), The number e, The MacTutor History of Mathematics archive, retrieved 02/02/2009
{{citation}}: Check date values in:|accessdate=و|date=(help) - ↑ Cajori, Florian (1991), A History of Mathematics (5th ed.), Providence, RI: AMS Bookstore, ISBN 978-0-8218-2102-2, p. 152
- ↑ ۲۲٫۰ ۲۲٫۱ Maor 2009, sections 1, 13
- ↑ Eves, Howard Whitley (1992), An introduction to the history of mathematics, The Saunders series (6th ed.), Philadelphia: Saunders, ISBN 978-0-03-029558-4, section 9-3
- ↑ Boyer, Carl B. (1991), A History of Mathematics, New York: John Wiley & Sons, ISBN 978-0-471-54397-8, p. 484, 489
- ↑ Bryant, Walter W., A History of Astronomy (PDF), London: Methuen & Co, archived from the original (PDF) on 5 October 2011, retrieved 22 August 2011, p. ۴۴
- ↑ Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0, section 2
- ↑ Abramowitz, Milton; Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (10th ed.), New York: Dover Publications, ISBN 978-0-486-61272-0, section 4.7. , p. 89
- ↑ Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: مکگرا-هیل, ISBN 978-0-07-145227-4, p. 264
- ↑ Devlin, Keith (2004), Sets, functions, and logic: an introduction to abstract mathematics, Chapman & Hall/CRC mathematics (3rd ed.), Boca Raton, Fla: Chapman & Hall/CRC, ISBN 978-1-58488-449-1, or see the references in function
- ↑ ۳۰٫۰ ۳۰٫۱ Lang 1997, section IV.2
- ↑ Stewart, James (2007), Single Variable Calculus: Early Transcendentals, Belmont: Thomson Brooks/Cole, ISBN 978-0-495-01169-9, section 1.6
- ↑ Lang, Serge (1997), Undergraduate analysis, Undergraduate Texts in Mathematics (2nd ed.), Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-94841-6, MR 1476913, section III.3
- ↑ "Calculation of d/dx(Log(b,x))". Wolfram Alpha. Wolfram Research. Archived from the original on 18 July 2011. Retrieved 15 March 2011.
- ↑ Kline, Morris (1998), Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, ISBN 978-0-486-40453-0, p. 386
- ↑ "Calculation of Integrate(ln(x))". Wolfram Alpha. Wolfram Research. Archived from the original on 18 July 2011. Retrieved 15 March 2011.
- ↑ Abramowitz & Stegun, eds. 1972, p. 69
- ↑ Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-60842-4, MR 1009558, section III.6
- ↑ Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5, sections 11.5 and 13.8
- ↑ Muller, Jean-Michel (2006), Elementary functions (2nd ed.), Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4372-0, sections 4.2.2 (p. 72) and 5.5.2 (p. 95)
- ↑ Hart, Cheney, Lawson; et al. (1968), Computer Approximations, SIAM Series in Applied Mathematics, New York: John Wiley
{{citation}}: Explicit use of et al. in:|author=(help)نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link), section 6.3, p. 105–111 - ↑ Zhang, M.; Delgado-Frias, J.G.; Vassiliadis, S. (1994), "Table driven Newton scheme for high precision logarithm generation" (PDF), IEE Proceedings Computers & Digital Techniques, 141 (5): 281–292, doi:10.1049/ip-cdt:19941268, ISSN 1350-387, archived from the original (PDF) on 9 May 2012, retrieved 2 September 2011
{{citation}}: Check|issn=value (help), section 1 for an overview - ↑ Meggitt, J. E. (1962), "Pseudo Division and Pseudo Multiplication Processes", IBM Journal, doi:10٫1147/rd.62٫0210
{{citation}}: Check|doi=value (help); Unknown parameter|month=ignored (help) - ↑ Kahan, W. (May 20, 2001), Psuedo-Division Algorithms for Floating-Point Logarithms and Exponentials
- ↑ ۴۴٫۰ ۴۴٫۱ Abramowitz & Stegun, eds. 1972, p. 68
- ↑ Sasaki, T.; Kanada, Y. (1982), "Practically fast multiple-precision evaluation of log(x)", Journal of Information Processing, 5 (4): 247–250, retrieved 30 March 2011
- ↑ Ahrendt, Timm (1999), Fast computations of the exponential function, Lecture notes in computer science, vol. 1564, Berlin, New York: Springer, pp. 302–312, doi:10.1007/3-540-49116-3_28
- ↑ Maor ۲۰۰۹, p. 135
- ↑ Frey, Bruce (2006), Statistics hacks, Hacks Series, Sebastopol, CA: O'Reilly, ISBN 978-0-596-10164-0, chapter 6, section 64
- ↑ Ricciardi, Luigi M. (1990), Lectures in applied mathematics and informatics, Manchester: Manchester University Press, ISBN 978-0-7190-2671-3, p. 21, section 1.3.2
- ↑ Maling, George C. (2007), "Noise", in Rossing, Thomas D. (ed.), Springer handbook of acoustics, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-30446-5, section 23.0.2
- ↑ Tashev, Ivan Jelev (2009), Sound Capture and Processing: Practical Approaches, New York: John Wiley & Sons, ISBN 978-0-470-31983-3, p. 48
- ↑ Chui, C.K. (1997), Wavelets: a mathematical tool for signal processing, SIAM monographs on mathematical modeling and computation, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-384-8, p. 180
- ↑ Wright, David (2009), Mathematics and music, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4873-9, chapter 5
- ↑ Bateman, P. T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, New Jersey: World Scientific, ISBN 978-981-256-080-3, OCLC 492669517, theorem 4.1
- ↑ P. T. Bateman & Diamond ۲۰۰۴, Theorem 8.15
- ↑ Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press, ISBN 978-0-412-35370-3, chapter 4
- ↑ Ganguly, S. (2005), Elements of Complex Analysis, Kolkata: Academic Publishers, ISBN 978-81-87504-86-3, Definition 1.6.3
- ↑ Nevanlinna, Rolf Herman; Paatero, Veikko (2007), Introduction to complex analysis, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4399-4, section 5.9
- ↑ Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, Singapore: World Scientific, ISBN 978-981-02-0246-0, section 1.2
منابع[ویرایش]
- ایوز، هاوارد و. (۱۳۸۱). آشنایی با تاریخ ریاضیات. ج. دوم. ترجمهٔ محمدقاسم وحیدی اصل. تهران: مرکز نشر دانشگاهی. شابک ۹۶۴-۰۱-۰۴۶۱-۲.
پیوند به بیرون[ویرایش]
- فیلمهای آموزشی دربارهٔ لگاریتم ایجاد شده از سوی کالین بایفلیت (Colin Byfleet)، بازبینی در ۱۲ سپتامبر ۲۰۱۱
- تفسیری بر کار نپر در لگاریتم ایجاد شده از سوی ادوارد رایت (Edward Wright)، بازبینی در ۱۲ سپتامبر ۲۰۱۱
- محاسبه لگاریتم به صورت ذهنی
| در ویکیانبار پروندههایی دربارهٔ لگاریتم موجود است. |



















![{\displaystyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca0e5324b82de66458079f9ed2b47bad05a6abbe)





















![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=b^{{\frac {1}{d}}\log _{b}(c)}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba9e10fbda0f1ce9dd2d211ec6bc2c80d1f3dd8)


























































![{\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55acf246da64ba711e1717eb43ad81792220ab32)



![{\displaystyle {\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76610ca7878ea438fa73bd50ac4df1fecce09b9f)


![{\displaystyle \log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/173477b6bc89e2396abacc83ca5015ac01b0747b)






![{\displaystyle \log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ccc3b05bf5ae0d41f85c50ab1a7ceec4e95713)












