قانون بنفورد
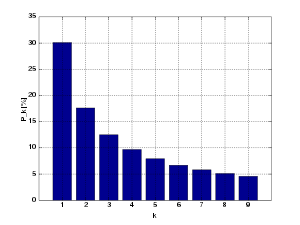
قانون بِنفورد (به انگلیسی: Benford's law) یا قانون رقم اول میگوید که در فهرست عددهایی که در بسیاری از (البته نه همهٔ) پدیدههای زندگی واقعی رخ میدهند، رقم اول عددها بهطور خاص و غیریکنواختی توزیع میشود. بر طبق این قانون، تقریباً در یکسوم موارد رقم نخست ۱ است، و عددهای بزرگتر در رقم نخست به ترتیب با بسامد کمتری رخ میدهند، و عدد ۹ کمتر از یک بار در هر بیست عدد ظاهر میشود.
علیرغم اینکه توزیع اعداد یا پدیدههای طبیعی معمولا از توزیع نرمال تبعیت میکنند رقم اول این اعداد از قانون بنفورد تبعیت میکنند. به بیان دیگر میتوان گفت که قانون بنفورد نوع دیگری از نمایش توزیع اعداد است که در آن اگر مجموعه اعدادی که رقم اول آنها ۱ و ۲ و ۳ و… است را کنار یکدیگر بگذاریم کل مجموعه را نمایش دادهایم.[۱] هرگاه که خود عددها بهطور لگاریتمی توزیع شده باشند، این توزیع رقمهای نخست منطقی خواهد بود. بنابر دلایلی، عددهایی که در سنجشهای واقعی ثبت میشوند، معمولاً توزیع لگاریتمی دارند.
این قانون به نام فرانک بنفورد فیزیکدان نامیده شدهاست، هرچند که پیش از آن سیمون نیوکام در سال ۱۸۸۱ آن را بیان کرده بود.
اگر چه قانون بنفورد قطعاً به بسیاری از مجموعه دادهها اعمال میشود، توضیح علمی آن[۲] اخیراً و در سال ۱۹۹۸ توسط هیل، ریاضیدان، با استفاده از قضایای حد مرکزی-گونه داده شدهاست.[۳] در حقیقت تا پیش از سال ۱۹۹۶ هیچکس نتوانست علت قانون بنفورد را به درستی توضیح دهد. سرانجام تئودور هیل (T. Hill) ثابت کرد که این قانون در سراسر جهان و حتی در دیگر دستگاههای شمارش مثل مبنای ۸ نیز صدق میکند. امروزه این قانون در حسابرسیهای قانونی به شکل گستردهای مورد استفاده قرار میگیرد، چرا که اگر حسابها با قانون بنفورد مطابقت نداشته باشند به این معنی خواهد بود که حسابها و اعداد به احتمال فراوان جعلی هستند.[۴] در کل قانون بنفورد یکی از بنیانهای روشهای کشف تقلب و کلاهبرداری است.[۵]
این قانون به ظاهر عجیب در بسیاری از دادهها برقرار است، مثلاً در صورتحسابهای برق، شمارهٔ خیابانها، قیمت سهام، مقدار جمعیت، آمار مرگومیر، طول رودخانهها، ثابتهای فیزیک و ریاضیات، و فرایندهایی که از توزیع توانی پیروی میکنند (که در طبیعت بسیار فراوانند). این قانون مستقل از پایهای که عددها در آن بیان میشوند برقرار است، هرچند که احتمال تکرار عددها در هر پایه متفاوت از پایههای دیگر است. بین آماردانان و دانشمندان علوم سیاسی در مورد اعمال پذیری قانون بنفورد به دادههای انتخاباتی اختلاف نظر وجود دارد. برخی مانند والتر میبین،[۶] استاد آمار و علوم سیاسی دانشگاه میشیگان معتقدند که رقم دوم دادهها از توزیع بنفورد پیروی میکند،[۷] در حالی که گزارش مرکز کارتر[۸] این دیدگاه را رد میکند.

منابع
- ↑ «دانشمند فرانسوی: قانون بنفورد تقلب در انتخابات ایران را ثابت میکند». صدای آلمان. ۲۹ خرداد ۱۳۸۸.
- ↑ Hill, T. P. "The First Digit Phenomenon." Amer. Sci. 84, 358-363, 1998
- ↑ Benford's Law, Wolfram Mathworld
- ↑ [۱] بایگانیشده در ۲۰ آوریل ۲۰۱۴ توسط Wayback Machine, Benford's law in auditing
- ↑ Varian, Hal (1972). "Benford's Law (Letters to the Editor)". The American Statistician. 26 (3): 65. doi:10.1080/00031305.1972.10478934.
- ↑ Walter R. Mebane, Jr.
- ↑ Walter R. Mebane, Jr., Note on the presidential election in Iran, June 2009 (PDF) (به انگلیسی) Retrieved on 2009-06-15.
- ↑ Carter Center (2005). Observing the Venezuela Presidential Recall Referendum: Comprehensive Report, Claim 4, p. 134
- مشارکتکنندگان ویکیپدیا. «Benford's law». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۵–۸–۲۰۱۰.
