توزیع مثلثی
از ویکیپدیا، دانشنامهٔ آزاد
|
تابع چگالی احتمال  | |||
|
تابع توزیع تجمعی 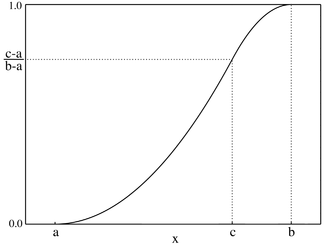 | |||
| پارامترها |
   | ||
|---|---|---|---|
| تکیهگاه |
 | ||
| تابع چگالی احتمال |
 | ||
| تابع توزیع تجمعی |
 | ||
| میانگین |
 | ||
| میانه |
 | ||
| مُد |
 | ||
| واریانس |
 | ||
| چولگی |
 | ||
| کشیدگی |
 | ||
| آنتروپی |
 | ||
| تابع مولد گشتاور |
 | ||
| تابع مشخصه |
 | ||
| |||||
|
این یک مقالهٔ خرد مربوط به آمار است. میتوانید با گسترش آن به ویکیپدیا کمک کنید. |
