آمار فرمی-دیراک

آمار فرمی-دیراک یا آمار F-D بخشی از علم فیزیک است که به توصیف انرژی ذراتِ تک، در یک سامانه می پردازد، این سامانه شامل تعداد زیادی ذره مشابهِ پیروی کننده از اصل طرد پاولی است. نام فرمی-دیراک پس از انریکو فرمی و پاول دیراک که هر دو به صورت جداگانه و هم‌زمان آن را کشف کرده بودند انتخاب شد.

آمار فرمی-دیراک در سامانه‌ای با تعادل دمایی، بر ذرات مساوی که گردش (اسپین) نیمه‌صحیح دارند اعمال می‌شود. همچنین فرض می‌شود که اندرکنش متقابل ذرات در این سامانه ناچیز است. این باعث می‌شود که بتوان این تعداد زیاد از ذرات را در وضعیت حالت پایهٔ یک تک‌ذره توصیف کرد. نتیجهٔ توزیع فرمی-دیراک بر روی این ذرات یعنی هیچ دو ذره‌ای نمی‌توانند حالت مشابه هم داشته باشند؛ که این نتیجه‌گیری تاثیر بزرگی بر روی ویژگی‌های سامانه دارد. از آنجایی که آمار فرمی-دیراک بر روی ذراتِ با گردش (اسپین) نیمه‌صحیح اعمال می‌شود، باید این ذرات را فرمیون خواند. این آمار بیشتر به الکترون‌هایی که خود فرمیون با گردش ۱/۲ اند اعمال می‌شود. آمار فرمی-دیراک خود زیرمجموعه‌ای از مکانیک آماری است و از اصول مکانیک کوانتوم پیروی می‌کند.

پیشینه

قبل از معرفی آمار فرمی-دیراک در سال ۱۹۲۶ فهم برخی از جنبه‌های رفتار الکترون به دلیل حضور پدیده‌های به ظاهر متناقض بسیار مشکل بود.

توزیع فرمی-دیراک

در سامانه‌ای با فرمیون‌های مساوی، اگر تعداد متوسط فرمیون‌های با حالت تک‌ذره $i$ در توزیع فرمی-دیراک به شکل زیر بیان می شود:

$\bar{n}_i = \frac{1}{e^{(\epsilon_i-\mu) / k T} + 1}$

که k ثابت بولتزمن است و T دمای مطلق و $\epsilon_i \$ انرژی یک ذره منفرد در حالت i و $\mu\$ پتانسیل شیمیایی است. در 0=T، پتانسیل شیمیایی برابر با انرژی فرمی است. درحالتی که الکترون ها در یک نیمه هادی قرار دارند $\mu\$ را تراز فرمی می نامیم.

توزیع فرمی-دیراک زمانی جواب درست می دهد که تعداد فرمیون ها آنقدر زیاد باشد که تغییر $\mu\$ ناشی از اضافه کردن یک فرمیون قابل صرف نظر کردن باشد. از آنجایی که توزیع فرمی-دیراک از اصل طرد پاولی مشتق شده درنتیجه داریم: $0 <\bar{n}_i <1$

• توزیع فرمی-دیراک
• 

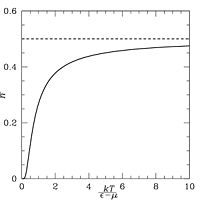
  وابستگی به انرژی. هرچه T بالاتر باشد، شیب نمودار ملایم تر است. برای $\bar{n}$ = 0.5 وقتی $\epsilon \;$ = $\mu \;$. نشان داده نشده است زیرا $\mu \$ برای T بالاتر افزایش می‌یابد.
  
• 

  وابستگی به دما برای $\epsilon> \mu \$ .

(برای بزرگ کردن عکس با نشانگر خود آن را انتخاب کنید.)

توزیع ذرات در انرژی

توزیع فرمی-دیراک که در بالا ارائه شد، توزیع ذرات مشابه فرمیون را در انرژی تک ذره بیان می دارد حالتی که گویی تنها یک فرمیون می تواند آن حالت انرژی را داشته باشد. درنتیجه با استفاده از توزیع فرمی-دیراک می توان توزیع انرژی فرمیونهای مشابه را چنان نشان داد که گویی بیش از یک فرمیون می تواند همان انرژی را داشته باشد.

تعداد متوسط فرمیونها با انرژی $\epsilon_i \$ را می توان با ضرب $\bar{n}_i \$ توزیع فرمی-دیراک در $g_i \$ (تعداد حالات با انرژی $\epsilon_i \$) بدست آورد:

$\begin{alignat}{2} \bar{n}(\epsilon_i) & = g_i \ \bar{n}_i \\ & = \frac{g_i}{e^{(\epsilon_i-\mu) / k T} + 1} \\ \end{alignat}$

وقتی که $g_i \ge 2 \$ باشد، امکان دارد که $\ \bar{n}(\epsilon_i)> 1$ زیرا بیش از یک حالت وجود دارد که می تواند توسط فرمیون های با انرژی $\epsilon_i \$ اشغال شود.

وقتی یک شبه زنجیره انرژی $\epsilon \$ چگالی حالت $g( \epsilon ) \$ دارد(به معنی تعداد حالات در یکای محدوده انرژی در یکای حجم). تعداد فرمیونهای متوسط در یکای محدوده انرژی در یکای حجم برابر است با:

$\bar { \mathcal{N} }(\epsilon) = g(\epsilon) \ F(\epsilon)$

که $F(\epsilon) \$ تابع فرمی نام دارد و همان تابعی است که در توزیع فرمی-دیراک $\bar{n}_i$ مورد استفاده قرار می گیرد.

$F(\epsilon) = \frac{1}{e^{(\epsilon-\mu) / k T} + 1}$

بنابراین

$\bar { \mathcal{N} }(\epsilon) = \frac{g(\epsilon)}{e^{(\epsilon-\mu) / k T} + 1}$ .

کوانتوم و نظام کلاسیک

آمار ماکسول-بولتزمان به عنوان تقریبی از آمار فرمی-دیراک برای مطالعه سیستم‌های فیزیکی که به اندازه کافی از حد تعیین شده توسط اصل عدم قطعیت هایزنبرگ فاصله دارند بدست می‌آید. شرایط کلاسیک که در آن آمار ماکسول-بولتزمان معتبر است، زمانی محقق می‌شود که فاصله متوسط میان دو ذره $\bar{R}$، خیلی بزرگتر از طول موج دو بروی $\bar{\lambda}$ باشد.

$\bar{R} \ \gg \ \bar{\lambda} \ \approx \ \frac{h}{\sqrt{3mkT}}$

در اینجا $h$ ثابت پلانک و $m$ جرم ذره‌است. در مورد الکترون‌های هادی در یک فلز معمولی در دمای 300=T کلوین (دمای اتاق) سامانه همچنان از نظام کلاسیک دور است زیرا $\bar{R} \approx \bar{\lambda}/25$ است. این مسئله از جرم کوچک الکترون و تمرکز زیاد الکترون‌های هادی ($\bar{R}$) در فلز است. بنابراین آمار فرمی-دیراک برای الکترون‌های هادی نوع فلز مورد نیاز است.

نمونه دیکر از سامانه‌ای که در نظام کلاسیک قرار ندارد، سامانه‌ای است که از الکترون‌های یک ستاره که متلاشی شده و به یک کوتوله سفید تبدیل شده‌است نام برد. هرچند که دما در کوتوله سفید بسیار بالا است (حدود 10،000 کلوین در سطح آن) باز به دلیل تمرکز الکترون هادی در آن و جرم بسیار کوچک الکترون در نظام کلاسیک جای نمی‌گیرد و آمار فرمی-دیراک مورد نیاز است.

منابع

مشارکت‌کنندگان ویکی‌پدیا، «Fermi–Dirac statistics»، ویکی‌پدیای انگلیسی، دانشنامهٔ آزاد (بازیابی در ۸ آوریل ۲۰۱۱).

پیوند به بیرون

• Fermi energy
• Maxwell–Boltzmann statistics
• Bose–Einstein statistics
• Parastatistics