هندسه جبری
برای تأییدپذیری کامل این مقاله به منابع بیشتری نیاز است. (اوت ۲۰۲۱) |

| هندسه |
|---|
 |
| فهرست هندسهدانان |
هندسهٔ جبری شاخهای از ریاضیات است که بهطور سنتی به مطالعهٔ صفرهای چندجملهایهای چند متغیره میپردازد. هندسهٔ جبری مدرن بر اساس استفاده از تکنیکهای جبر مجرد بنا شده که اساساً از جبر جابجایی استفاده میکند تا مسائل هندسی مربوط به این مجموعه صفرها (ریشه این چند جملهایها) را مطالعه کند.
اشیای بنیادی که در مطالعه هندسه جبری استفاده میشوند واریتههای جبریاند که بیان هندسی حل دستگاهی از معادلات چند جملهایاند. بیشترین واریتههای جبری مطالعه شده خمهای جبری صفحهاند که شامل خطوط، دایرهها، سهمیها، بیضیها، هذلولیها، خمهای مکعبی مثل خمهای بیضوی و خمهای درجه چهار مثل lemniscateها و Cassini ovalها میباشند. یک نقطه از صفحه به خم بیضوی متعلق است اگر مختصات آن در یک معادلهٔ چند جملهای دادهشده صدق کند. سوالات بنیادی مربوط به مطالعهٔ نقاط خاصی مثل نقاط تکین، نقاط عطف و نقاط در بینهایت میباشد. سوالات پیشرفتهتر مرتبط میشوند به توپولوژی خم و معادلات بین خمهای داده شده بهوسیله معادلات مختلف.
هندسه جبری نقش محوری در ریاضیات مدرن ایفا کرده و پیوندهای مفهومی چندگانهای با شاخههای گستردهای از ریاضیات چون آنالیز مختلط، توپولوژی و نظریه اعداد دارد. در ابتدا مطالعهٔ دستگاه معادلات چند جملهایهای چند متغیره موضوع هندسه جبری بود، آنجا که حل معادله از نظر خارج شده و فهمیدن خواص ذاتی جواب دستگاه معادلات اهمیت بیشتری پیدا میکند، آنجاست که هندسه جبری ظاهر میشود؛ چرا که در این مرحله دیگر یک جواب خاص اهمیت چندانی در مقابل آن خواص ندارد، این ما را به برخی قلمروها میکشاند که برخی از آنها جزو عمیقترین قلمروهای ریاضی هستند، چه از نظر مفهومی یا تکنیکی.
در قرن بیستم، هندسه جبری به چندین زیرمجموعه تقسیمبندی شدند:
- جریان اصلی هندسه جبری به مطالعه نقاط مختلط واریتههای جبری و بهطور عمومیتر نقاطی که مختصات آنها در میدان بسته جبری قرار دارند میپردازد.
- هندسه جبری حقیقی به مطالعه نقاط حقیقی یک واریته جبری میپردازد.
- هندسه سیالهای و بهطور عمومیتر هندسهٔ حساب به مطالعهٔ نقاط یک واریته جبری که مختصاتشان در میدانهای غیر بسته قرار دارند میپردازد، مثل میدانهایی که در نظریه جبری اعداد بحث میشوند چون اعداد گویا، میدانهای عددی، میدانهای متناهی، میدان توابع و میدان p-adicها.
- بخش عمده نظریه تکینگی به تکینگیهای واریتههای جبری میپردازد.
- هندسه جبری محاسباتی قلمرویی است که با ظهور رایانهها از برخورد هندسه جبری و جبر رایانهای بهوجود آمدهاست. این قلمرو عمدتاً شامل طراحی الگوریتم و توسعه نرمافزار برای مطالعه خواص بارز یک واریته داده شده میباشد.
بسیاری از پیشرفتهای جریان اصلی هندسه جبری در قرن بیستم در چارچوب جبر مجرد، صورت گرفت، با افزایش تأکید بر روی خواص «ذاتی» واریتههای جبری که وابسته به هیچکدام از روشهای متفاوت جاسازی آن واریته در فضای مختصاتی اطرافیش (ambient) وابسته نباشد؛ این هدف موازی با پیشرفت در شاخههایی چون توپولوژی، هندسه دیفرانسیل و هندسه مختلط میباشد. یکی از دستاوردهای کلیدی این هندسه جبری مجرد، نظریه اسکیم گروتندیک است که اجازه استفاده از نظریه شیفها برای مطالعهٔ واریتههای جبری را داده به طوری که این نحوه استفاده، شباهت بسیاری به استفاده از آن در مطالعه منیفلدهای دیفرانسیل و تحلیلی دارد. این دستاورد با توسعهٔ مفهوم نقطه بهوجود آمد؛ در هندسه جبری کلاسیک، یک نقطه از واریته آفین را از طریق قضیه صفرهای هیلبرت میتوان شناسایی کرد، بهوسیله یک ایدهآل ماکسیمال حلقه مختصاتی، در حالی که نقطه متناظر با آن در اسکیم آفین، همگی ایدهآلهای اولی از این حلقه میباشند. این بدین معناست که یک نقطه از چنین اسکیمی میتواند یا یک نقطه عادی، یا یک زیرواریته باشد. همچنین این رویکرد موجب اتحاد زبان و ابزارهای هندسه جبری کلاسیک گشته که بهطور عمده با نقاط مختلط، و نظریه جبری اعداد مرتبط میگردد. اثبات وایلز بر حدس فرما به نام قضیه آخر فرما که به مدت طولانی، حلناشدنی باقی مانده بود، اثباتی بر قدرت این رویکرد میباشد.
تاریخچه[ویرایش]
قبل از قرن شانزدهم[ویرایش]
برخی از ریشههای هندسه جبری به قبل از کارهای یونانیان هلنی قرن پنجم قبل از میلاد می. رسد. به عنوان مثال، مسئله تضعیف مکعب این بود که چگونه میتوان پاره خطی به طول x ساخت به گونهای که حجم مکعبی به ضلع x برابر مکعب مستطیلی به ابعاد a2b باشد که در آن a و b به ما داده شدهاند. منایخموس (حدود ۳۵۰ قبل از میلاد) این مسئله را به صورت هندسی، با بررسی دو مخروط ay = x2 و xy = ab مورد بررسی قرار داد.[۱] اتفاق بعدی، در قرن سوم قبل از میلاد، مطالعهٔ نظاممند ارشمیدس و آپولونیوس بر روی مسائل مقاطع مخروطی بود[۲] که در آن از مفهوم مختصات استفاده شد.[۱] ریاضیدانان عرب قادر بودند برخی معادلات مکعبی را صرفاً با روشهای خالص جبری حل کرده، سپس نتایج را به وسیله هندسه، تفسیر کنند. این کار توسط ابن هیثم نیز در قرن ۱۰ بعد از میلاد انجام شد.[۳] سپس ریاضیدان فارسیزبان، خیام (متولد ۱۰۴۸ پس از میلاد) روشی برای حل معادلات مکعبی با استفاده از تقاطع یک دایره و سهمی کشف کرد[۴] و به نظر میرسد که اولین شخصی بود که نظریه عمومی معادلات درجه سوم را درک کرده باشد.[۵] چند سال پس از عمر خیام، کتاب شرفالدین طوسی به عنوان المعادلات به عنوان «آغاز راه هندسه جبری» توصیف گشت.[۶]
رنسانس[ویرایش]
چنین تکنیکهایی از کاربرد ساختارهای هندسه در مسائل جبری توسط برخی ریاضیدانان عصر رنسانس نیز چون جرلامو کاردانو و نیکلو تارتالیا نیز در مطالعاتشان بر روی معادلات مکعبی به کار گرفته شد. ریاضیدانان قرن شانزدهم و هفدهم، رهیافت هندسی برای ساخت مسائل را در مقابل روشهای جبری ترجیح میدادند، بهخصوص بلیز پاسکال که در مقابل استفاده از روشهای جبری و تحلیلی در هندسه موضع میگرفت.[۷] ریاضیدانان فرانسوی چون فرانسوا ویت و سپس رنه دکارت و پیر دو فرما انقلابی در روش قراردادی تفکر در مورد ساخت مسائل از طریق هندسه تحلیلی بهوجود آوردند. آنها در آغاز، علاقهمند به خواص خمهای جبری، مانند آن خمهایی که در معادلات سیالهای (در مورد فرما) تعریف میشوند و همچنین به فرمولبندی جبری کارهای یونانیان در مقاطع مخروطی و درجه سه (در مورد دکارت) علاقه نشان میدادند.
در همین دوره بود که بلیز پاسکال و ژرارد دوسارگ به هندسه از رهیافت دیگری وارد شده و به توسعه مفاهیم هندسهٔ تصویری پرداختند. پاسکال و دزارگ نیز به مطالعه خمها پرداختند؛ اما از دیدگاه صرفاً هندسی آن، یعنی مشابه روش یونانیان، ساخت (رسم) با خطکش و پرگار. در نهایت، هندسه تحلیلی دکارت و فرما ازین نبرد پیروز درآمد؛ چرا که برای ریاضیدانان قرن هجدهم ابزارهای کمی ملموس مورد نیاز آنها را برای مطالعه مسائل فیزیکی با استفاده از حسابان نیوتون و لایبنیز فراهم نمود. با این حال، در پایان قرن هجدهم، اکثر جنبهٔ جبری هندسه تحلیلی (هندسه مختصاتی) توسط لاگرانژ و اویلر تحت عنوان حساب بینهایت کوچکها طبقهبندی شد.
قرن نوزدهم و اوایل قرن بیستم[ویرایش]
دو رده تحقیقات همزمان بر روی هندسه نااقلیدسی و انتگرالهای آبلی در قرن نوزدهم موجب شدند تا ایدههای جبری این دفعه به سوی هندسی خود بازگردند. اولین تلاشها توسط ادموند لاگر و آرتور کیلی صورت گرفت که تلاش کردند تا خواص متری تعمیمیافتهٔ فضای تصویری را تعیین کنند. کیلی ایده فرمهای چندجملهای همگن را معرفی کرد، بهویژه فرمهای درجه دو بر روی فضای تصویری. سپس فلیکس کلاین هندسهٔ تصویری (به همراه انواع دیگر هندسه) را از این نقطه نظر، مورد مطالعه قرار داد که اطلاعات هندسه روی یک فضا در تبدیلهای آن فضا کدگذاری شدهاند. در پایان قرن نوزدهم، هندسهدانان تصویری انواع عمومیتری از تبدیلها را روی شکلهای فضای تصویری مطالعه میکردند. به جای تبدیلهای خطی تصویری که معمولاً به عنوان ایجاد کنندهٔ هندسه کلاینی بنیادی روی فضای تصویری در نظر گرفته میشدند، آنها خود را درگیر تبدیلات دوسرگویا (birational)ی درجه بالاتر نیز کردند. این مفهوم تناسب ضعیفتر بعدها در قرن بیستم موجب شد که اعضای مکتب هندسه جبری ایتالیایی رویههای جبری را در حد یکریختی دوسرگویا (birational isomorphism) طبقهبندی کنند.
پیشرفتهای اوایل قرن نوزدهم، یعنی انتگرالهای آبلی منجر شد که برنهارت ریمان رویههای ریمانی را توسعه دهد.
در همان دوره، جبریسازی هندسه جبری از طریق جبر جابجایی صورت گرفت. نتایج عمدهٔ این جهتگیری قضیهٔ پایه هیلبرت و قضیه صفرهای هیلبرت بود که پایه ارتباط بین هندسه جبری و جبر جابهجایی بوده، و همچنین برآیندهای (resultants) چند متغیره که پایه نظریهٔ حذف (elimination) میباشد. احتمالاً به دلیل حجم محاسباتی که برآیندهای چند متغیره طلب میکنند، نظریهٔ حذف در طی قرن بیستم به فراموشی سپرده شد تا این که توسط نظریهٔ تکینگی و هندسهٔ جبری محاسباتی مجدداً احیا گشت.[الف]
قرن بیستم[ویرایش]
ون در واردن، اسکار زاریسکی و آندره ویل بنیان هندسه جبری را بر اساس جبر جابجایی معاصر بنا نهادند که شامل نظریه ارزیافت و نظریه ایدهآلها میشد. یکی از هدفهایشان ارائه چارچوبی محکم برای اثبات نتایج مکتب ایتالیایی هندسه جبری بود. بهخصوص این که این مکتب بهطور نظاممند از مفهوم نقطه جنریک استفاده کرد؛ در حالی که هیچ تعریف دقیقی برای آن ارائه ندادند؛ آنها اولین تعریفی که برای این گونه نقاط ارائه دادند در طی دهه ۱۹۳۰ بود.
در دهه ۵۰ و ۶۰ میلادی، ژان پیر سر و الکساندر گروتندیک بنیانها را مجدداً قالببندی کردند و در این مسیر از نظریه شیف، استفاده کردند. سپس از حدود ۱۹۶۰ همراه با دستگاه ابزارهای پالوده شدهٔ تکنیکهای هومولوژی، روی ایدهٔ اسکیمها کار شد که بیشتر این تلاشها به رهبری گروتندیک بود. پس از یک دهه پیشرفت سریع، این شاخه در دهه ۱۹۷۰ پایدار گشت، و کاربردهای جدیدی ایجاد شد، هم در نظریه اعداد و هم در سوالات کلاسیکتری که در هندسه در مورد واریتههای جبری، تکینگیها، فضاهای مدولی، و فضاهای مدولی فرمال وجود داشت.
یک دسته مهم از واریتهها که به راحتی، مستقیماً از معادلاتی که آنها را تعریف میکنند شناخته نمیشوند، واریتههای آبلی هستند، که واریتههای تصویری هستند که نقاطشان یک گروه آبلی تشکیل میدهند. مثالهای نوعی اینگونه واریتههای خمهای بیضوی میباشند که برای خود نظریهٔ غنی ای دارند. این واریتهها در اثبات آخرین قضیه فرما نقش کلیدی داشته و همچنین در رمزنگاری با خمهای بیضوی مورد استفاده قرار گرفتهاند.
موازی با روند مجرد هندسه جبری که به دنبال احکام عمومی واریته هاست، روشهای محاسباتی مؤثری برای واریتههای ملموس نیز توسعه یافتهاند که منجر به عصر جدیدی از هندسه جبری محاسباتی میگردد. یکی از روشهای بنیادی این قلمرو نظریه پایههای گروبنر است که توسط برونو بوچبرگر در ۱۹۶۵ معرفی گشت. یکی دیگر از روشهای پایهای، بهطور خاص به هندسه جبری حقیقی اختصاص دارد، این روش تجزیه جبری استوانهای میباشد که توسط جورج ای. کالینز در ۱۹۷۳ معرفی شدهاست.
مفاهیم پایه ای[ویرایش]
صفرهای همزمان چند جمله ایها[ویرایش]
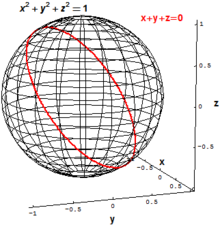
در هندسه جبری کلاسیک، علاقه اصلی بر روی اشیایی بود که بهطور همزمان مجموعهای از چند جملهایها را ناپدید میکنند (صفر میکنند)، یعنی مجموعه نقاطی که همزمان در یک یا تعداد بیشتری از معادلات چندجملهای صدق میکنند. به عنوان مثال، کره دوبُعدی با شعاع ۱ در فضای اقلیدسی را میتوان به صورت مجموعه تمام نقاط (x,y,z)ی تعریف کرد که در این معادله، صدق میکنند:
یک دایرهٔ «اریب» در را میتوان به صورت مجموعه نقاط (x,y,z) تعریف کرد که در دو معادلهٔ چندجملهای زیر، همزمان، صدق میکنند:
واریتههای آفین[ویرایش]
مقاله اصلی: واریتههای آفین[ویرایش]
ابتدا با یک میدان شروع میکنیم. در هندسه جبری کلاسیک، این میدان، همیشه میدان اعداد مختلط بود؛ اما بسیاری از نتایج با فرض یک میدان جبری بستهای چون هم، معتبر باقی خواهند ماند. ما فضای آفین بعدی روی را در نظر گرفته و آن را با نمایش میدهیم (یا صرفاً با ، هنگامی که در متن واضح باشد). هنگامی که دستگاه مختصات ثابت و مشخص باشد، میتوان را با یکی گرفت. هدف کار نکردن با این است که ساختار فضای برداری که با خود حمل میکند «فراموش» شود.
یک تابع را چندجملهای (یا منظم) گویند اگر آن را بتوان به صورت چندجملهای نوشت، یعنی اگر وجود داشته باشد چندجملهای چون در به گونهای که برای هر نقطه با مختصات در داشته باشیم .
هنگامی که یک دستگاه مختصات، انتخاب شد، توابع منظمِ روی n-فضای آفین را میتوان با حلقه توابع چندجملهای n متغیره روی یکی گرفت؛ به همین دلیل، مجموعه توابع منظم روی حلقه است و آن را با نمایش میدهند.
یک چندجملهای، در نقطهای ناپدید میشود اگر که مقدارش در آن نقطه، صفر شود. فرض کنید مجموعه تمام چندجملهایهای درون باشد. مجموعه ناپدیدشونده (یا مکان هندسی ناپدیدشونده یا مجموعه صفر) مجموعه شامل تمام نقاط درون است که هر چندجملهای در بر روی آن، ناپدید میشوند؛ بهطور نمادین:
برای مجموعهای چون ، زیرمجموعه از را مجموعه جبری میگویند. مخفف کلمه varietry است (یک نوع خاص از مجموعههای جبری که در ادامه، تعریف شدهاست).
فرض کنید که مجموعهای مثل از داده شده باشد، آیا میتوان مجموعه تمام چندجملهایهایی که آن را تولید کردهاند را یافت؟ اگر زیرمجموعه دلخواهی از باشد، را به این صورت تعریف کنید: مجموعه تمام چندجملهایهایی که مجموعه صفرشان شامل باشد. اول کلمه ایدهآل است: اگر دو چندجملهای و هر دو روی ناپدید (صفر) شوند، آنگاه هم روی ناپدید میشود، و اگر یک چندجملهای دلخواه باشد، آنگاه هم روی ناپدید شده؛ به همین دلیل، همیشه یک ایدهآل از حلقه چندجملهایهای است.
دو پرسش طبیعی، پیش میآید:
- برای یک زیرمجموعه دلخواه از ، چه زمان ؟
- برای یک مجموعه دلخواه از چندجملهایها چون ، چه زمان ؟
جواب سؤال اول با معرفی توپولوژی زاریسکی داده شد، یک توپولوژی روی که مجموعههای بسته آن، همان مجموعههای جبری هستند که بهطور مستقیم ساختار جبری را انعکاس میدهند. آنگاه اگر و تنها اگر یک مجموعه جبری یا یک مجموعه بسته زاریسکی باشد. جواب سؤال دوم توسط قضیه صفرهای هیلبرت داده میشود. یکی از شکلهای این قضیه میگوید که رادیکال ایدهآلهای تولید شده توسط است. به بیان مجردتر، یک ارتباط گالوایی، وجود دارد که منجر به ظهور دو عملگر بستار میگردد؛ آنها را میتوان شناسایی کرده و بهطور طبیعی، نقش بنیادینی در این نظریه بازی میکنند؛ مثال مربوط در بحث مربوط به ارتباط گالوایی، تشریح شدهاست.
به دلایل مختلف، ممکن است همیشه نخواهیم با کل ایدهآل مربوط به یک مجموعه جبری چون کار کنیم. قضیه بنیادی هیلبرت میگوید که ایدهآلهای درون همیشه متناهی، تولید شدهاند.
یک مجموعه جبری را تحویلناپذیر گویند اگر نتوان آن را به صورت اجتماع دو مجموعه جبری کوچکتر نوشت. هر مجموعه جبری به صورت اجتماع متناهی مجموعههای جبری تحویلناپذیر بوده و این تجزیه یکتاست؛ لذا عناصر آن را مؤلفههای تحویلناپذیر آن مجموعه جبری گویند. به یک مجموعه جبری تحویلناپذیر واریته هم میگویند. مشخص میشود که یک مجموعه جبری واریته (مجموعه جبری تحویلناپذیر) است اگر و تنها اگر به صورت مجموعه ناپدیدکننده (صفر کننده) یک ایدهآل اول از حلقه چندجملهای باشد.
برخی از مؤلفان، تمایز مشخصی بین مجموعههای جبری و واریتهها برقرار نمیکنند و در صورت لزوم از اصطلاح واریته تحویلناپذیر برای ایجاد چنین تمایزی استفاده میکنند.
توابع منظم[ویرایش]
مقاله اصلی: تابع منظم
درست همانگونه که توابع پیوسته نگاشتهای طبیعی روی فضاهای توپولوژی و توابع هموار نگاشتهای طبیعی روی منیفلدهای دیفرانسیلپذیر اند، دسته ای طبیعی از توابع روی یک مجموعه جبری نیز وجود دارند که به آنها توابع منظم یا توابع چندجمله ای گویند. یک تابع منظم روی مجموعه ای جبری چون در ، تحدید توابع منظم روی به مجموعه جبری است. برای یک مجموعه جبری که روی میدان اعداد مختلط تعریف شده باشد، توابع منظم هموار و حتی تحلیلی اند.
ممکن است الزام توسعه پذیر بودن یک تابع منظم به کل فضای پیرامونی (ambient) بهطور غیرطبیعی محدود کننده به نظر آید، اما این کار شباهت بسیاری به شرایط فضای توپولوژیکی نرمال دارد که در آن قضیه توسعه تیتز تضمین میکند که یک تابع پیوسته روی یک مجموعه بسته همیشه به فضای توپولوژیکی پیرامونی توسعه یابد.
توابع منظم روی ، درست همانند توابع منظم روی فضای آفینی، تشکیل یک حلقه میدهند که با نمایش داده میشود. این حلقه را حلقه مختصاتی روی مینامند.
از آنجا که توابع منظم روی از توابع منظم روی نشأت میگیرند، رابطه ای بین حلقههای مختصاتیشان وجود دارد. بهخصوص، اگر یک تابع منظم روی V تحدید دو تابع و در باشد، آنگاه هم یک تابع چند جمله ای خواهد بود که روی ناپدید شده و لذا به تعلق خواهد داشت. ازینرو، را میتوان با یکی گرفت.
کاربردها[ویرایش]
هندسه جبری اکنون در آمار،[۸] نظریه کنترل،[۹][۱۰] رباتیک،[۱۱] کدهای تصحیح-کننده خطا،[۱۲] فیلوژنتیک[۱۳] و مدلسازی هندسی.[۱۴] همچنین ارتباطاتی با نظریه ریسمان،[۱۵] نظریه بازی،[۱۶] تطابق گراف،[۱۷] سالیتونها[۱۸] و برنامهریزی صحیح.[۱۹]
جستارهای وابسته[ویرایش]
یادداشتها[ویرایش]
- ↑ شاهدی بر این نسیان، این حقیقت است که ون در واردن فصل مربوط به نظریه حذف را از ویرایش سوم (و تمام ویرایشهای بعدی) کتاب خویش، یعنی رساله جبر مدرن حذف نمود.
ارجاعات[ویرایش]
- ↑ ۱٫۰ ۱٫۱ Dieudonné, Jean (1972). "The historical development of algebraic geometry". The American Mathematical Monthly. 79 (8): 827–866. doi:10.2307/2317664. JSTOR 2317664.
- ↑ Kline, M. (1972) Mathematical Thought from Ancient to Modern Times (Volume 1). Oxford University Press. pp. 108, 90.
- ↑ Kline, M. (1972) Mathematical Thought from Ancient to Modern Times (Volume 1). Oxford University Press. p. 193.
- ↑ Kline, M. (1972) Mathematical Thought from Ancient to Modern Times (Volume 1). Oxford University Press. pp. 193–195.
- ↑ St Andrews بایگانیشده در ۲۰۱۷-۱۱-۱۲ توسط Wayback Machine "Khayyam himself seems to have been the first to conceive a general theory of cubic equations."
- ↑ Rashed (1994, pp.102-3)
- ↑ Kline, M. (1972) Mathematical Thought from Ancient to Modern Times (Volume 1). Oxford University Press. p. 279.
- ↑ Drton, Mathias; Sturmfels, Bernd; Sullivant, Seth (2009). Lectures on Algebraic Statistics. Springer. ISBN 978-3-7643-8904-8.
- ↑ Falb, Peter (1990). Methods of Algebraic Geometry in Control Theory Part II Multivariable Linear Systems and Projective Algebraic Geometry. Springer. ISBN 978-0-8176-4113-9.
- ↑ Tannenbaum, Allen (1982). Invariance and Systems Theory: Algebraic and Geometric Aspects. Lecture Notes in Mathematics. Vol. Volume 845. Springer-Verlag. ISBN 978-3-540-10565-7.
{{cite book}}:|volume=has extra text (help) - ↑ Selig, J. M. (2005). Geometric Fundamentals of Robotics. Springer. ISBN 978-0-387-20874-9.
- ↑ Tsfasman, Michael A.; Vlăduț, Serge G.; Nogin, Dmitry (1990). Algebraic Geometric Codes Basic Notions. American Mathematical Soc. ISBN 978-0-8218-7520-9.
- ↑ Cipra, Barry Arthur (2007). "Algebraic Geometers See Ideal Approach to Biology" (PDF). SIAM News. 40 (6). Archived from the original (PDF) on 3 March 2016.
- ↑ Jüttler, Bert; Piene, Ragni (2007). Geometric Modeling and Algebraic Geometry. Springer. ISBN 978-3-540-72185-7.
- ↑ Cox, David A.; Katz, Sheldon (1999). Mirror Symmetry and Algebraic Geometry. American Mathematical Soc. ISBN 978-0-8218-2127-5.
- ↑ Blume, L. E.; Zame, W. R. (1994). "The algebraic geometry of perfect and sequential equilibrium". Econometrica. 62 (4): 783–794. doi:10.2307/2951732. JSTOR 2951732.
- ↑ Kenyon, Richard; Okounkov, Andrei; Sheffield, Scott (2003). "Dimers and Amoebae". arXiv:math-ph/0311005.
- ↑ Fordy, Allan P. (1990). Soliton Theory A Survey of Results. Manchester University Press. ISBN 978-0-7190-1491-8.
- ↑ Cox, David A.; Sturmfels, Bernd. Manocha, Dinesh N. (ed.). Applications of Computational Algebraic Geometry. American Mathematical Soc. ISBN 978-0-8218-6758-7.
برای مطالعه بیشتر[ویرایش]
- بعضی کتب کلاسیک که از نظر تاریخی قبل از اسکیم ها هستند:
- van der Waerden, B. L. (1945). Einfuehrung in die algebraische Geometrie. Dover.
- Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 1. Cambridge University Press. ISBN 978-0-521-46900-5. Zbl 0796.14001.
- Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 2. Cambridge University Press. ISBN 978-0-521-46901-2. Zbl 0796.14002.
- Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 3. Cambridge University Press. ISBN 978-0-521-46775-9. Zbl 0796.14003.
- کتابهای مرجع مدرن که از زبان اسکیم ها استفاده نمیکنند:
- Garrity, Thomas; et al. (2013). Algebraic Geometry A Problem Solving Approach. American Mathematical Society. ISBN 978-0-8218-9396-8.
- Griffiths, Phillip; Harris, Joe (1994). Principles of Algebraic Geometry. Wiley-Interscience. ISBN 978-0-471-05059-9. Zbl 0836.14001.
- Harris, Joe (1995). Algebraic Geometry A First Course. Springer-Verlag. ISBN 978-0-387-97716-4. Zbl 0779.14001.
- Mumford, David (1995). Algebraic Geometry I Complex Projective Varieties (2nd ed.). Springer-Verlag. ISBN 978-3-540-58657-9. Zbl 0821.14001.
- Reid, Miles (1988). Undergraduate Algebraic Geometry. Cambridge University Press. ISBN 978-0-521-35662-6. Zbl 0701.14001.
- Shafarevich, Igor (1995). Basic Algebraic Geometry I Varieties in Projective Space (2nd ed.). Springer-Verlag. ISBN 978-0-387-54812-8. Zbl 0797.14001.
- کتابهایی در مورد هندسه جبری محاسباتی
- Cox, David A.; Little, John; O'Shea, Donal (1997). Ideals, Varieties, and Algorithms (2nd ed.). Springer-Verlag. ISBN 978-0-387-94680-1. Zbl 0861.13012.
- Basu, Saugata; Pollack, Richard; Roy, Marie-Françoise (2006). Algorithms in real algebraic geometry. Springer-Verlag.
- González-Vega, Laureano; Recio, Tómas (1996). Algorithms in algebraic geometry and applications. Birkhaüser.
- Elkadi, Mohamed; Mourrain, Bernard; Piene, Ragni, eds. (2006). Algebraic geometry and geometric modeling. Springer-Verlag.
- Dickenstein, Alicia; Schreyer, Frank-Olaf; Sommese, Andrew J., eds. (2008). Algorithms in Algebraic Geometry. The IMA Volumes in Mathematics and its Applications. Vol. 146. Springer. ISBN 978-0-387-75155-9. LCCN 2007938208.
- Cox, David A.; Little, John B.; O'Shea, Donal (1998). Using algebraic geometry. Springer-Verlag.
- Caviness, Bob F.; Johnson, Jeremy R. (1998). Quantifier elimination and cylindrical algebraic decomposition. Springer-Verlag.
- کتابهای مرجع در مورد اسکیم ها:
- Eisenbud, David; Harris, Joe (1998). The Geometry of Schemes. Springer-Verlag. ISBN 978-0-387-98637-1. Zbl 0960.14002.
- Grothendieck, Alexander (1960). Éléments de géométrie algébrique. Publications Mathématiques de l'IHÉS. Zbl 0118.36206.
- Grothendieck, Alexander; Dieudonné, Jean Alexandre (1971). Éléments de géométrie algébrique. Vol. 1 (2nd ed.). Springer-Verlag. ISBN 978-3-540-05113-8. Zbl 0203.23301.
- Hartshorne, Robin (1977). Algebraic Geometry. Springer-Verlag. ISBN 978-0-387-90244-9. Zbl 0367.14001.
- Mumford, David (1999). The Red Book of Varieties and Schemes Includes the Michigan Lectures on Curves and Their Jacobians (2nd ed.). Springer-Verlag. ISBN 978-3-540-63293-1. Zbl 0945.14001.
- Shafarevich, Igor (1995). Basic Algebraic Geometry II Schemes and complex manifolds (2nd ed.). Springer-Verlag. ISBN 978-3-540-57554-2. Zbl 0797.14002.
پیوند به بیرون[ویرایش]
- Foundations of Algebraic Geometry by Ravi Vakil, 808 pp.
- Algebraic geometry entry on PlanetMath
- English translation of the van der Waerden textbook
- Dieudonné, Jean (March 3, 1972). "The History of Algebraic Geometry". Talk at the Department of Mathematics of the University of Wisconsin–Milwaukee – via YouTube.
- The Stacks Project, an open source textbook and reference work on algebraic stacks and algebraic geometry













![{\displaystyle k[x_{1},...,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c94122b5f7993f4d088b504b7118b4d914b35d1)




![{\displaystyle k[\mathbb {A} ^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5a59ad2c4843393bb4e679b7982dc8388adb233)

















![{\displaystyle K[V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec5fddcd6d55d1d9c792a53117274e8637be0e33)
![{\displaystyle K[\mathbb {A} ^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eddfb520d34a5fc2ea02f3745d0d9095b357d3f)


![{\displaystyle K[\mathbb {A} ^{n}]/I(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/077cdda9824e05053091314f21558055f7d1dab5)