هذلولی

تصویری از یک هذلولی

از سلسله مقالاتی دربارهٔ مقاطع مخروطی
سهمی
معادله	$y^{2}=4ax\,$
گریز از مرکز ($e$)	$1\,$
نیم‌راست‌وتر کانونی ($l$)	$2a\,$
هذلولی
معادله	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$
گریز از مرکز ($e$)	${\sqrt {1+{\frac {b^{2}}{a^{2}}}}}$
نیم‌راست‌وتر کانونی ($l$)	${\frac {b^{2}}{a}}$
بیضی
معادله	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$
گریز از مرکز ($e$)	${\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$
نیم‌راست‌وتر کانونی ($l$)	${\frac {b^{2}}{a}}$
دایره (حالت خاص بیضی)
معادله	$x^{2}+y^{2}=a^{2}\,$
گریز از مرکز ($e$)	$0$
نیم‌راست‌وتر کانونی ($l$)	$a$
• • •

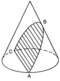
هُذلولی یا اَبَرپَرته (برگردانِ گرته‌برداشته) (به انگلیسی: Hyperbola)، خمی باز است که از برخورد یک صفحه با سطح مخروطی، در حالتی که صفحه، موازی با محورِ سطحِ مخروطی باشد، پدید می‌آید. در صفحهٔ اقلیدسی و از نظر مکان هندسی، هذلولی مجموعه‌ای از نقاط در یک صفحه است که تفاضل فاصلهٔ هر یک از آن‌ها از دو نقطهٔ ثابت در صفحه (کانون‌ها)، مقداری ثابت (دو برابر مقدار a در هذلولی) باشد؛ اگر نصف اندازهٔ طول و عرض هذلولی را a و b و نصف فاصلهٔ کانونی را c بنامیم، در هر هذلولی رابطهٔ c² = a² + b² برقرار خواهد بود. هر هذلولی دو خط مجانب دارد که در مرکز هذلولی با هم برخورد می‌کنند.

تاریخچه

یونان باستان

بنابر تقریظی از اراتوستن، هذلولی را نخستین‌بار منایخموس (۳۸۰ — ۳۲۰ پ. م)، دوست نزدیک افلاطون، در تلاش برای حل تضعیف مکعب (ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض است فقط با استفاده از خط‌کش و پرگار) کشف کرد. آپولونیوس برای اولین بار نام «اوپربولی» ((به یونانی: υπερβολή)، به معنای «بیشتر بودن») را بر روی هذلولی گذاشت و اقلیدس (حدود ۳۶۵–۲۷۵ پ. م) بررسی دقیقی از ویژگی‌های هذلولی ارائه کرد. پاپوس اسکندرانی (حدود ۳۵۰ — ۲۹۰ پ. م) مفهوم خط‌های هادی را برای نخستین بار بررسی کرد و نشان داد که هر منحنی یکتا نسبت ثابتی (که بعدها به برون‌مرکزی معروف شد) دارد و این نسبت ثابت برای هذلولی‌ها همیشه بیشتر از ۱ است.

نام آپولونیوس (اواخر قرن سوم — اوایل قرن دوم پیش از میلاد) برای قرن‌ها پس از مرگ او با مطالعهٔ مقاطع مخروطی گره خورده بود. آپولونیوس اثر مهمش «مخروطات» را، که مشتمل بر هشت مقاله است، با مطالعهٔ مخروط آغاز می‌کند و پس از تعریف سه مقطع مخروطی (سهمی، هذلولی، و بیضی)، به تعریف خط مماس آن‌ها می‌پردازد و سپس ثابت می‌کند که فاصلهٔ کانونی برای همهٔ نقاط روی یک هذلولی ثابت است.

قرون وسطی

همزمان با حکومت مأمون در خراسان (در قرن سوم هجری)، اخوان ثلاثهٔ بنوموسی دست به ترجمهٔ مخروطات آپولونیوس از یونانی به عربی زدند. بنوموسی فقط نسخه‌ای ناقص از مخروطات را در اختیار داشتند و مقاطع مخروطی در زمان ایشان به دست فراموشی سپرده شده بود، بنابراین در فهم متن دچار مشکل بودند. اندکی بعد، یکی از اخوان ثلاثه به نام حسن نظریهٔ مقاطع استوانه‌ای را ابداع کرد که می‌توان آن را مقدمه‌ای ساده بر مقاطع مخروطی دانست. پس از درگذشت حسن، برادرش احمد در شام نسخه‌ای کامل‌تر از چهار فصل اول مخروطات را با شرح اوتوکیوس پیدا کرد و به کمک برادر دیگرش، محمد، و با استفاده از دو نسخهٔ موجود و نظریهٔ حسن، موفق شد نظریات آپولونیوس را دریابد. احمد و محمد ترجمهٔ مقالهٔ اول تا چهارم مخروطات را به هلال حمصی و مقالهٔ پنجم تا هفتم آن را به ثابت بن قره سپردند و خود بازنگری نهایی ترجمه را عهده‌دار شدند. ترجمهٔ برادران بنوموسی از مقالات پنجم تا هفتم مخروطات تنها نسخهٔ باقی ماندهٔ این اثر است. ترجمهٔ آثار علمی به عربی اغلب نیازمند ابداع اصطلاحات فنی تازه بود و مترجمان آن‌ها، بر خلاف مترجمان لاتین، به ترانویسی عبارات یونانی اکتفا نکردند و برای واژهٔ «اوپربول» اصطلاح «قطع زائد» را در نظر گرفتند که معنای آن را حفظ می‌کند و هنوز در زبان عربی به هذلولی «قطع زائد» گفته می‌شود.

رنسانس و قرون جدید

اسحاق نیوتن در کتاب «اصول ریاضی فلسفه طبیعی» نشان داد که اگر نیروی کشش میان اجسام آسمانی متناسب با معکوس مجذور فاصله بین آن دو باشد، اجرامی که به دور یک جرم بزرگ می‌گرداند، یا باید حرکت دایره‌ای، بیضوی، سهموی یا هذلولوی داشته باشند. نیوتن از هذلولی برای محاسبه مدار اجرام سماوی استفاده کرد.

رنه دکارت خود مقاطع مخروطی آپولونیوس را در آثارش در باب هندسه تحلیلی بررسی کرده بود.

معادلهٔ استاندارد

معادلهٔ هذلولی به مرکز $(h,k)$ به فرم استاندارد به صورت زیر است:

${\begin{cases}\displaystyle {\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1&{\mbox{horizontal transversive axis}}\\\displaystyle {\frac {(y-k)^{2}}{a^{2}}}-{\frac {(x-h)^{2}}{b^{2}}}=1&{\mbox{vertical transversive axis}}\end{cases}}$

شکل پارامتریک معادلهٔ هذلولی به یکی از سه صورت زیر خواهد بود:

$$1:{\begin{cases}x=\pm a\,{\text{cosh}}(t)+h\\y=b\,{\text{sinh}}(t)+k\end{cases}},\quad t\in \mathbb {R}$$

$$2:{\begin{cases}x=\pm a\,{\frac {t^{2}+1}{2t}}+h\\y=b\,{\frac {t^{2}-1}{2t}}+k\end{cases}},\quad t\neq 0$$

$$3:{\begin{cases}x=a\,{\text{sec}}(t)+h\\y=\pm b\,{\text{tan}}(t)+k\end{cases}},\quad 0\leq t<2\pi ,\,t\neq {\frac {\pi }{2}},\,t\neq {\frac {3\pi }{2}}$$

ویژگی‌ها

• معادلهٔ هذلولی با جایگزینی یک عملگر در معادلهٔ بیضی به‌دست می‌آید:
• $b^{2}.x^{2}-a^{2}.y^{2}-a^{2}.b^{2}=0$ که مرکز آن $O(0,0)$ است. ورتکس‌های آن $(a,0)$ و $(-a,0)$ هستند و نقاط $(0,b)$ و $(0,-b)$ روی هذلولی قرار ندارند بلکه روی محور تقارن آن هستند.
• مستطیلی که مرکز $O$ باشد و طول اضلاعش $a$ و $b$، قطرهایش مجانب‌های هذلولی هستند ($u$ و $v$).
• هر هذلولی دو شاخه دارد که تا بینهایت به مجانب‌های آن نزدیک می‌شوند. کشیدن شاخه‌ها در رسم دقیق هذلولی‌ها اهمیت دارد.

برای هر هذلولی می‌توان دو نقطه تمرکز $F_{1}(e,0)$ و $F_{2}(-e,0)$ ساخت به شکلی که $e^{2}=a^{2}+b^{2}$. می‌توان نشان داد که تفاضل فواصل هر نقطه روی هذلولی از این دو نقطه برای هر هذلولی ثابت و برابر $2a$ است:

• $|dist(P_{0},F_{1})-dist(P_{0},F_{2})|=2a$

منابع

فهرست منابع

• Pottmann, Helmut; Asperl, Andreas; Hofer, Michael; Kilian, Axel; Bentley, Daril (2007). Architectural geometry. Bentley Institute Press. ISBN 1-934493-04-X. OCLC 180177477.

منابع

• Larson, Ron (2010). Trigonometry. Cengage Learning. ISBN 1-4390-4907-6.