تعامد (جبر خطی)

در ریاضیات، دو بردار را متعامد[۱] (به انگلیسی: Orthogonal) گویند هرگاه برهم قائم باشند. به عبارت دیگر دو بردار متعامدند اگر و تنها اگر ضرب داخلی آنها برابر با صفر باشد یا با هم زاویهٔ راست (۹۰ درجه) ساخته باشند.
تعریفها[ویرایش]
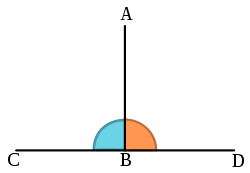
- در هندسه، دو بردار اقلیدسی عمود بر هم هستند اگر به بکدیگر قائم باشن؛ یعنی هم زاویه قائم بسازند.
- دو بردار و را در یک فضای ضرب داخلی برهم عمودند اگر ضرب داخلی صفر باشد. این رابطه تعامد را با نشان میدهند.
- دو زیرفضای برداری و از یک فضای ضرب داخلی را زیرفضاهای متعامد میگوییم اگر هر بردار از به هر بردار از عمود باشد. بزرگترین زیرفضایی که به یک زیرفضا عمود باشد، متمم عمود آن نامیده میشود.
- یک نگاشت خطی را نگاشت خطی متعامد میگوییم اگر ضرب داخلی را پایسته نگه دارد. یعنی برای هر جفت بردار و در فضای ضرب داخلی داشته باشیم:
این یعنی زاویهٔ بین و را ثابت نگه میدارد و طول و برابر است.
دستهای از بردارهای دوبهدو عمود برهم را که طول واحد داشته باشند (بردار یکّه باشند) بردارهای یکّه راستهنجار (متعامد یکه) مینامیم.
توابع متعامد[ویرایش]
مرسوم است که برای توابع و ضرب داخلی زیر را تعریف کنیم:
که در آن تابع وزن نامنفی برای ضرب داخلی است. در ساده ترین حالت w(x) = 1. در این صورت، اگر حاصل ضرب داخلیشان صفر باشد میگوییم دو تابع برهم عمودند:
با استفاده از ضرب داخلی، ما نُرم به صورت زیر تعریف میکنیم که عبارت است از ضرب داخلی بردار در خودش. نُرم، طول بردارها (تابعها) را به دست مید:
اعضای یک دنباله از توابع {fi : i = 1, 2, 3, ...} متعامد هستند اگر
و راستهنجار (متعامد یکه) هستند اگر:
در رابطهٔ بالا
دلتای کرونکر نام دارد. به زبان دیگر هر دو عضوی از این دنباله برهم عمودند و طولشان (برای توابع راستهنجار) ۱ است. چندجملهایهای متعامد را ببینید.
مثالها[ویرایش]
- بردارهای (۱, ۳, ۲)، (۳, −۱, ۰) و (۱/۳, ۱, −۵/۳) برهم عمودند، زیرا

(۱)(۳) + (۳)(−۱) + (۲)(۰) = ۰
(۳)(۱/۳) + (−۱)(۱) + (۰)(−۵/۳) = ۰
(۱)(۱/۳) + (۳)(۱) − (۲)(۵/۳) = ۰
- دو تابع 2t + ۳ و 5t2 + t − ۱۷/۹ را در نظر بگیرید. این تابعها در بازهٔ و با تابع وزن برهم عمودند. ضرب این دو تابع برابر است با 10t3 + 17t2 − 7/9 t − ۱۷/۳ و ضرب داخلیشان میشود:
- چندجملهایهای متعامد بسیاری هستند که در ریاضیات، علوم و مهندسی کاربردهای بیشماری دارند. مانند:
- در مکانیک کوانتومی، دو ویژهحالت یک تابع موج و متعامد هستند اگر مربوط به ویژهمقدارهای متفاوتی باشند. به زبان نمادگذاری دیراک، مگر این که و متعلق به یک ویژهمقدار باشند.
در آرایهشناسی[ویرایش]
در آرایهشناسی یک طبقهبندی متعامد است که در آن در هیچ موردی، هیچ عضوی در بیش از یک گروه عضو نباشد، این به معنی منحصر به فرد بودن متقابل طبقهبندیها و عضوها است.
جستارهای وابسته[ویرایش]
منابع[ویرایش]
- ↑ «بُردارهای متعامد» [ریاضی] همارزِ «orthogonal vectors»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر پنجم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۹۶۴-۷۵۳۱-۷۶-۴ (ذیل سرواژهٔ بُردارهای متعامد)
- مشارکتکنندگان ویکیپدیا. «Orthogonality». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲ مه ۲۰۱۵.
کتابهای رایگان برخط[ویرایش]
- محمد خرمی (تابستان ۲۰۰۳). «جبر خطی» (PDF). بایگانیشده از اصلی (PDF) در ۳۱ ژانویه ۲۰۱۲. دریافتشده در ۲۹ مارس ۲۰۰۹.
- Beezer, Rob, A First Course in Linear Algebra
- Connell, Edwin H. , Elements of Abstract and Linear Algebra
- Hefferon, Jim, Linear Algebra excellent textbook with complete solutions manual





















![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![{\displaystyle \int _{-1}^{1}\left(10t^{3}+17t^{2}-{7 \over 9}t-{17 \over 3}\right)\,dt=\left[{5 \over 2}t^{4}+{17 \over 3}t^{3}-{7 \over 18}t^{2}-{17 \over 3}t\right]_{-1}^{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9deaa9ea03e06b9163c5c14f3a9c4801cd55a2fb)





