آشنایی با نسبیت عام
| بخشی از سری مقالات در مورد: |
| نسبیت عام |
|---|
 |

نسبیت عام نظریهای علمی برای گرانش است که آلبرت اینشتین در سالهای بین ۱۹۰۵ و ۱۹۱۵ گسترش داد. این نظریه باعث شد که دیدگاه قبلی از فضا به عنوان موجودی ایستا (استاتیک) و تنها به عنوان مکانی که در آن رویدادهای فیزیکی اتفاق میافتند، کنار گذاشته شود. بهجای آن، فضازمان بهعنوان موجودی پویا (دینامیک) و تغییر شکلدهنده در نظر گرفته میشود که حضور ماده در آن، ساختار و هندسهٔ آن را خمیده میکند و در مقابل، حرکت اجسام تحت گرانش از خمیدگی فضازمان پیروی مینماید. به بیان دیگر، اجسام همواره — چه در فضای تهی بدون گرانش و چه در حضور ماده و انرژی و در نتیجه، گرانش — در طول مستقیمترین مسیر ممکن حرکت میکنند و حضور جرم و انرژی تنها شکل این مسیرها را در فضازمان — از خطوط مستقیم در فضای تهی به مسیرهایی خمیده در حضور جرم و انرژی — تغییر میدهد که به معنای خمیده شدن فضازمان است؛ یعنی گرانش به عنوان یک عامل هندسی و نه یک نیرو بررسی میگردد.[۱]
در آغاز قرن بیستم، قانون جهانی گرانش نیوتن برای مدتی بیش از ۲۰۰ سال به عنوان توصیف پذیرفته شده برای گرانش بین اجسام مطرح بود. در این مدل، گرانش ناشی از نیرویی جذبکننده بین دو جسم — با سازوکاری نامعین — است. هرچند خودِ نیوتن نیز با طبیعت ناشناخته این نیرو مشکل داشت[۲] و برخی مسائل نظیر انتشار این نیرو با سرعت بینهایت مبهم بود، این مدل برای توصیف حرکت تحت گرانش بسیار موفق ظاهر گردید: حرکت سیارات در سامانهٔ خورشیدی را به خوبی توصیف میکرد و زمان ظاهر شدن ستارگان دنبالهدار را به دقت پیشبینی مینمود.[۳]
با اینحال مشاهدهها و آزمایشها نشان میدهند که توصیف اینشتین از گرانش (نسبیت عام)، پدیدههایی را پیشبینی میکند که توسط نظریه نیوتنی قابل پیشبینی نیستند. برای مثال میتوان به ناهنجاریهای کوچک مشاهدهشده در مدار حرکت برخی سیارات نظیر عطارد اشاره کرد. علاوه بر این، نسبیت عام پدیدههای جدیدی را هم پیشبینی میکند، مانند همگرایی گرانشی، موجهای گرانشی و اثر گرانش بر روی زمان که به اتساع زمان گرانشی معروف است. بسیاری از این پدیدهها تاکنون از طریق آزمایش تأیید شدهاند، و در مورد برخی نیز در حال حاضر جستجو ادامه دارد. برای مثال، مشاهدهٔ امواج گرانشی برای نخستین بار در سال ۲۰۱۶ و پس از گذشت صد سال از پیشبینی اینشتین در مورد وجود این امواج، به کمک تأسیسات لایگو (LIGO) صورت پذیرفت،[۴][۵] هرچند قبلاً وجود این امواج بهطور غیرمستقیم تأیید شدهبود.[۶]
نسبیت عام، چندی پس از ظهور به ابزاری اساسی در اخترفیزیک تبدیل شد. برای نمونه، این نظریه اساسِ درکِ فعلیِ ما از سیاهچالهها را تشکیل میدهد. در این مناطق، گرانش بهقدری شدید است که هیچ چیز حتی نور نمیتواند از آن بگریزد. تصور میشود که گرانشِ نیرومندِ آنها عامل تابشهای شدید گسیلشده از برخی اجرام نجومی است (مانند هسته کهکشانی فعال یا ریزاختروشها). نسبیت عام، همچنین سهم عمدهای در چارچوب مهبانگ در کیهانشناسی دارد.
در قرن گذشته با وجود پژوهشهای فراوان، پیشرفت اندکی فراتر از دیدگاههای خود اینشتین به دست آمدهاست. نظریه نسبیت عام نظریهای کامل نیست و هنوز پرسشهای بیپاسخی باقی ماندهاند. بنیادیترین آنها چگونگی آشتی دادن نسبیت عام و مکانیک کوانتومی برای ایجاد نظریهای کامل و خود–سازگار به نام گرانش کوانتومی است.
از نسبیت خاص تا نسبیت عام[ویرایش]
در سپتامبر ۱۹۰۵، آلبرت اینشتین نظریهٔ نسبیت خاص را منتشر کرد که قوانین حرکت نیوتن را با الکترودینامیک ماکسول (قوانین حاکم بر اندرکنش بین اجسام دارای بار الکتریکی) آشتی میدهد. نسبیت خاص با معرفیِ مفاهیمِ جدیدی از فضا و زمان، چارچوب جدیدی را برای همهٔ فیزیک پایهریزی نمود. در این هنگام مشخص گردید که برخی از قوانین پذیرفتهشدهٔ فیزیک، با این چارچوب جدید ناسازگارند. یک نمونهٔ مهم، قانون جهانی گرانش نیوتون بود که نیروی متقابل بین دو جسم ناشی از جرمشان را نشان میدهد.[۷]
برخی فیزیکپیشهها از جمله اینشتین، سعی در یافتن نظریهای کردند که بتواند قوانین گرانش نیوتن را با نسبیت خاص، سازگار کند. در این بین، تنها نظریهٔ اینشتین توانست با نتایج آزمایشها و مشاهدهها مطابقت داشتهباشد. برای درک مفاهیم بنیادی این نظریه، خوب است روند فکری اینشتین در سالهای ۱۹۰۷ تا ۱۹۱۵ را دنبال کنیم، از آزمایش فکری سادهٔ او در مورد ناظرِ در حال سقوط آزاد تا نظریهٔ کاملاً هندسی او از گرانش.[۸]
اصل همارزی[ویرایش]
شخصی در یک آسانسورِ در حال سقوط آزاد، بیوزنی را تجربه میکند و اجسام نیز یا بیحرکت میمانند یا با سرعت ثابت به مسیر خود ادامه میدهند. بهدلیل اینکه همهچیز در آسانسور با هم حرکت میکنند، هیچ اثر گرانشیای را نمیتوان مشاهده کرد؛ یعنی، مشاهدههای ناظرِ در سقوط آزاد با مشاهدات ناظرِ در فضای بیکران و به دور از هرگونه منشأ گرانش با هم یکسان هستند. این ناظرها، ناظرهایی هستند که در نسبیت خاص در مورد آنها بحث میشود، ناظرهایی که برای آنها نور با سرعت ثابت و در مسیر مستقیم منتشر میشود.[۹]
اینشتین فرض کرد که مشاهدات یکسانِ ناظرِ در حالت بیوزنی با ناظر در حرکت لَخت در نسبیت خاص، یکی از ویژگیهای بنیادی گرانش است و این اصل را یکی از پایههای نظریهٔ خود قرار داد و آن در قالب اصل همارزی بیان نمود. به بیان واضحتر، طبق این اصل، شخصی در یک آسانسورِ در حال سقوط، نمیتواند متوجه سقوطِ آزادِ خود شود و آن را از حرکت در فضایی به دور از هر جرمی تفکیک دهد. نتیجهٔ هر آزمایشی که در این شرایط انجام شود با نتیجهٔ دیدهشده در یک فضاپیمای ساکن (یا حرکتکننده با سرعت ثابت) در فضای بیکران به دور از هر جرم و منشأ گرانشی، یکسان خواهد بود.[۱۰]
گرانش و شتاب[ویرایش]

بیشتر اثرات گرانش هنگام سقوط آزاد ناپدید میشوند، اما این اثرات را میتوان در یک چارچوب مرجع شتابدار مشاهده کرد، بهعبارت دیگر، ناظری در یک اتاق بسته (یِ کوچک) نمیتواند موارد زیر را تفکیک کند:
- اجسام به پایین سقوط میکنند، زیرا اتاق روی زمین است و گرانش زمین، آن اجسام را جذب میکند.
- اجسام به پایین سقوط میکنند، زیرا اتاق روی یک موشک در فضای دور با شتاب ۹٫۸۱ متر بر مجذور ثانیه در حال شتابگیری است و هیچ منشأ گرانشی وجود ندارد. اجسام به دلیل همان شبهنیرویی که رانندهٔ در حال شتاب گرفتن در خودرو را به صندلی میچسباند، رو به کف اتاق شتاب میگیرند.[۱۱]
بهطور مشابه، همه اثرات فیزیکی دیده شده در چارچوبی شتابدار، باید در میدانی گرانشی با شدت معادل، مشاهده شوند. این اصل، موجب شد تا انیشتین چند اثر جدید از گرانش را پیشبینی کند که در قسمت بعدی به آنها اشاره شدهاست.
برای به حساب آوردن نیروهای وارد بر اجسام در یک چارچوب مرجع شتابدار باید نیروهایی را که در فیزیک به آنها شبهنیرو میگویند به حساب آوریم. یک مثال که همان راننده در خودروی در حال شتابگیری است پیشتر آورده شد. بینش عمیق اینشتین دریافتِ این نکته بود که این کششِ ناشی از گرانش اساساً با این شبهنیروها یکسان است.[۱۲] همچنین، مقدار این شبهنیروها همواره متناسب با جرم جسم است، همانگونه که در قانون گرانش نیوتون آورده شدهاست. به بیان واضحتر جرم گرانشی با جرم لَخت (کمیت وارد شده در قانون دوم نیوتون) برابر است و جسم حاضر در میدان گرانشی نیرویی متناسب با جرم خود احساس میکند.[۱۳]
نتایج فیزیکی اصل همارزی[ویرایش]
در سال ۱۹۰۷، اینشتین هنوز ۸ سال با کامل کردن نسبیت عام فاصله داشت. با اینحال توانست با استفاده از اصل همارزی، که نقطهٔ شروع کار او برای گسترش نظریه جدیدش بود و نیز نتایج نسبیت خاص، برخی پیشبینیهای جدید و قابل مشاهده را مطرح کند.[۱۴]

نخستین موردِ جدید، تغییر بسامد نور بر اثر گرانش بود. پدیدهٔ انتقال به سرخ (یا انتقالبهآبی) به این شکل قابلِ بیان است:
دو ناظر را روی یک موشکِ در حالِ شتابگیری در نظر بگیرید. روی این موشک، یک جهتِ بالا و یک جهتِ پایین به صورت طبیعی تعریف میشود. جهت بالا جهتی است که موشک در آن جهت در حال شتابگیری است. حال فرض کنید که یکی از ناظرها بالاتر از دیگری ایستادهاست. وقتی ناظر پایینی یک سیگنال نوری برای ناظر بالایی میفرستد، شتاب چارچوب مرجع موجب روی دادن پدیدهٔ انتقال به سرخ برای نور میشود، که از نسبیت خاص قابل محاسبه است، و این ناظر، بسامد را کمتر از مقدار اندازهگیری شده با فرستنده اندازه میگیرد. بهعکس، اگر ناظرِ بالایی سیگنالی برای پایینی بفرستد، انتقالبهآبی روی خواهد داد و گیرنده بسامد بالاتری را اندازه خواهد گرفت.[۱۵]
اینشتین بیان کرد که این پدیده باید در یک میدان گرانشی نیز مشاهده شود. این مسئله در شکل سمت چپ نشان دادهشدهاست، که نشان میدهد بسامد نور با دور شدن از جرم در جهت خلاف میدان گرانشی کاهش مییابد. این پدیده از طریق آزمایش نیز تأیید گردید. در ادامه نوشتار در این باره توضیح دادهشدهاست.
انتقال بسامد گرانشی مربوط به اتساع زمان گرانشی است: ناظر بالایی برای یک طول موج، بسامد کمتری را از ناظر پایینی اندازه میگیرد، بنابراین زمان باید برای ناظر بالایی سریعتر بگذرد. در نتیجه زمان برای ناظرهای پایینتر در یک میدان گرانشی کندتر میگذرد.
باید توجه داشت که از دید هر ناظر، هیچ تفاوتی در جریانِ زمان برای پدیدهها و اتفاقاتی که در چارچوب آن ناظر در حال سکونند مشاهده نمیشود، غذا در همان مدت همیشگی میپزد و با گذشت یک سال، شخص ناظر به همان اندازه پیر میشود. به عبارت بهتر، هر ساعت با اتفاقاتی که در مجاورت آن روی میدهد مطابقت کامل دارد. تنها هنگام مقایسه بین چند ناظر مختلف است که میتوان گفت زمان کندتر یا تندتر میگذرد.[۱۶] این اثر نیز به صورت تجربی در چندین آزمایش تأیید شدهاست که در پایین آمدهاست.
همچنین اینشتین انحراف گرانشی مسیر نور را پیشبینی کرد: در یک میدان گرانشی، نور به سمت جرم خمیده میشود. از نظر عددی، مقداری که او در آن هنگام به دست آورد، که تنها با استفاده از اصل همارزی بود، یک ضریب ۲ با مقدار اصلی تفاوت داشت. نتیجهٔ درست پس از فرمولبندیِ کاملِ نظریه به دست آمد.[۱۷]
اثرات کشندی[ویرایش]

همارزی بین اثرات گرانشی و لَختی نظریهٔ کاملی از گرانش را تشکیل نمیدهند. برای مثال هنگام توضیح اثرات گرانش روی سطح زمین، با توجه به اینکه چارچوب مرجع ما در حال سقوط آزاد نیست، شبهنیروها وارد عمل میشوند و بنابراین توضیح مناسبی برای آثار گرانش بر اجسام روی سطح زمین قابل ارائه است. اما ناظر در حال سقوط آزاد در یک طرف زمین نمیتواند توضیح دهد که چرا به اجسامِ سمتِ دیگرِ زمین، نیرویی در جهتِ مخالف وارد میشود.
نتیجهٔ سادهتر دیگری از این اثر، هنگام بررسی حرکت دو جسم که در کنار هم به سمت زمین در حال سقوط هستند مشاهده میشود. در چارچوبی که در کنار این اجسام در حال سقوط آزاد است به نظر میرسد که آنها در کنار هم شناور هستند ـ اما نه بهطور دقیق؛ زیرا این اجسام به سمت یک نقطه (مرکز جرم زمین) در حال شتابگیریاند و در نتیجه یک مؤلفهٔ حرکت به سمتِ یکدیگر نیز دارند. (شکل را ببینید) برای دو جسمِ نزدیک به هم، این اثر کوچک است٬اما برای دو چترباز در در حال سقوط در سمتهای مخالف زمین (که حرکتشان کاملاً در جهت مخالف هم است) این اثر بزرگ است. این تفاوتها در نیرو، مسئول پدیدهٔ جزر و مد در اقیانوسها نیز هستند. به همین دلیل نام اثرات کشندی (جز و مد) برای این پدیدهها به کار میرود.[۱۸]
همارزی بین اینرسی و گرانش نمیتواند اثرات کشندی را توضیح دهد — تغییرات میدان گرانشی را در نظر نمیگیرد.[۱۹] به همین دلیل، نظریهای برای توصیف چگونگی تأثیر ماده (مانند جرم عظیم زمین) بر روی فضای لَختِ اطراف خود مورد نیاز است.
از شتاب تا هندسه[ویرایش]
اینشتین، هنگام بررسی همارزیِ گرانش با شتاب و نیز نقش نیروهای کشندی، چندین شباهت با هندسه سطوح پیدا کرد. یک نمونه تبدیل شدن چارچوب مرجع لَخت (که در آن ذرات در امتداد خطوط مستقیم و با سرعت ثابت حرکت میکنند) به چارچوب مرجع چرخان (که در آنها عبارات اضافهای برای در نظر گرفتن شبهنیروها وارد معادلات حرکت میشوند) است: این تغییر، همانند گذار از دستگاه مختصات دکارتی (که خطوط مختصات، خطوطی مستقیماند) به مختصات خمیدهخط (که خطوط مختصات الزاماً مستقیم نیستند) است.
یک شباهت عمیقتر، نیروهای کشندی را به یک ویژگیِ سطوح به نام انحنا مرتبط میکند. در یک میدان گرانشی و در یک دستگاه مرجع در حال سقوط آزاد، میتوان اثرات ناشی از حضور گرانش را با در نظر گرفتن نیروهای کشندی به حساب آورد. بهطور مشابه، حضور یا عدم حضور انحنا در یک فضا، تعیین میکند که یک سطح، یک صفحه است یا خیر. در تابستان ۱۹۱۲، اینشتین که این شباهتها را دریافته بود شروع به جستجو برای یک فرمولبندی هندسی برای گرانش نمود.[۲۰]
اشیاءِ بنیادیِ هندسه ـ نقطه، خط، مثلث و نظیر اینهاـ بهطور معمول در فضای سه بعدی یا روی سطوح دو بعدی تعریف میشوند. در سال ۱۹۰۷، هرمان مینکوفسکیِ ریاضیدان (که از استادهای سابق ریاضی اینشتین در پلیتکنیک فدرال سوئیس بود) یک فرمولبندی هندسی از نظریهٔ نسبیت خاص اینشتین ارائه کرد که در آن، هندسه علاوه بر فضا شامل زمان نیز میبود.
موجود اصلی این هندسه جدید، فضازمانِ چهاربعدی است. مسیرهایِ اجسامِ در حال حرکت، در حالت کلی منحنیهایی در فضا زمان هستند. مدارهای اجسامی که با سرعت ثابت حرکت میکنند خطوطی مستقیماند.[۲۱]
برای سطوح، تعمیم هندسهٔ یک صفحه (ی تخت) به یک سطح خمیده در حالت کلی را کارل فریدریش گاوس در اوایل قرن نوزدهم انجام داده بود. این کار برای فضاهای با ابعاد بالاتر را برنهارد ریمان در دههٔ ۱۸۵۰ انجام داده بود. با کمک هندسه ریمانی، اینشتین توانست یک توصیف هندسی از گرانش را فرمولبندی کند که در آن فضازمان مینکوفسکی با یک فضازمانِ خمیده شده و اعوجاج یافته جایگزین شدهبود. درست همانطور که سطوح خمیده تعمیمی از صفحه (سطح مستقیم) هستند.[۲۲]
بعد از اینکه او متوجه درستی این شباهت هندسی شد، سه سال دیگر طول کشید تا بتواند ستون باقیماندهٔ نظریهٔ خود را بیابد: معادلات توصیفکنندهٔ چگونگی تأثیر ماده بر خمیدگی فضازمان. بعد از به دست آوردن معادلاتی که امروزه با نام معادلات اینشتین (یا بهطور دقیقتر، معادلات میدان گرانشی) شناخته شده هستند، او نظریهٔ جدید خود را در اواخر سال ۱۹۱۵ طی چند مرحله و در نهایت در تاریخ ۲۵ نوامبر به فرهنگستان علوم پروس ارائه نمود.[۲۳]
هندسه و گرانش[ویرایش]
به گفتهٔ جان ویلر، نظریهٔ هندسیِ گرانشِ اینشتین را میتوان چنین خلاصه کرد:
در سه قسمت زیر به معنای این جمله پرداخته شدهاست. ابتدا مفهوم خمیدگی فضازمان و بعد از آن، حرکت ذرهای به نام ذرهٔ آزمون و نیز ویژگیهای ماده به عنوان منشأ گرانش بررسی میشود؛ در پایان نیز معادلاتِ اینشتین آورده میشوند که برخی ویژگیهای ماده را به انحنای فضازمان مربوط میکنند.
مفهوم خمیدگی فضازمان[ویرایش]
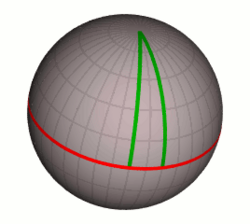
خمیدگی فضازمان یکی از کمیتهای اساسی نظریه نسبیت عام است. برای شروع بحث دربارهٔ معنای خمیدگی فضازمان این سؤال را مطرح میکنیم: چگونه میتوان به خمیدگی فضازمان پی برد؟ فضازمان یک فضای چهاربعدی است و تصور آن دشوار است؛ برای به دست آوردن تصویری از مفهوم خمیدگی یک فضا در حالت کلی، سطح زمین را که فضایی دو بعدی است در نظر بگیرید. برای فهمیدن اینکه سطح زمین خمیدهاست، میتوان به سادگی زمین را ترک کرد و از درون هواپیما یا از فضا خمیدگی آن را مشاهده کرد. اما فرض کنید موجودی دوبعدی (یا، بهطور تقریبی، بسیار کوچک مانند یک مورچه) که نمیتواند از فضای سطح زمین خارج شود سعی در بررسی خمیدگی این فضا دارد. همانطور که در تصویر سمت چپ نمایش داده شدهاست، این موجودات میتوانند با ترسیم یک مثلث و اندازهگیری زاویههای درون آن ـ که بیشتر از ۱۸۰ درجه خواهد بود ـ یا بهطور معادل، با رسم دو خط که در استوا موازیاند و در قطبها به هم میرسند (برخلاف هندسهٔ اقلیدسی، که با سطوح بدون خمیدگی سروکار دارد) به وجود انحنا در سطح با همان خمیدگی آن پی ببرند.
همانند این موجودات دوبعدی که در فضای دوبعدی سطح زمین قرار دارند و قادر به ترک این فضا نیستند، ما نیز در فضازمان زندگی میکنیم و امکان ترک آن برای ما وجود ندارد. آن موجودات میتوانند از اطلاعاتی که به دست میآورند به خمیدگی فضازمان پی ببرند، ما نیز میتوانیم با اطلاعاتی که در دست داریم به خمیدگی فضازمان پی ببریم.
همچنین، همانطور که مقدار انحنای سطح زمین برای همهٔ نقاط آن عدد ثابتی نیست و برای مثال، در قلهٔ کوهها بیشتر از سطح اقیانوسها است، خمیدگی فضازمان نیز در نقاط مختلف آن متفاوت است. در ادامه خواهیم دید که این خمیدگی ناشی از حضور ماده (و یا انرژی) در یک نقطه از فضازمان است.[۲۵]
ژئودزیکها[ویرایش]
در یک فضای خمیده، مفهوم خط راست با مفهوم ژئودزیک جایگزین میشود. برای موجودات دوبعدی در فضای دوبعدی سطح زمین، مسیری که استوا را به قطب متصل میکند (در شکل) یک خط مستقیم به نظر میرسد. این خطوط مستقیم در فضاهای خمیده، ژئودزیک نام دارند. ژئودزیکها کوتاهترین مسیر ممکن بین دو نقطه در یک فضا هستند.
یک مثال ساده از مفهوم ژئودزیک، چنین است: در ژئودزی، دانش اندازهگیری شکل و اندازهٔ زمین، یک ژئودزیک کوتاهترین مسیر بین دو نقطه روی سطح زمین است. بهطور تقریبی این مسیر قطعهای از یک دایره عظیمه مانند یک نصفالنهار یا خط استوا است. این خطوط یقیناً راست نیستند، چراکه باید از انحنای سطح زمین تبعیت کنند، اما تحت این محدودیت (الزام حرکت روی سطح منحنی زمین)، این خطوط راستترین خطوط ممکن بین دو نقطهاند.[۲۶]
برخی ویژگیهای ژئودزیکها با ویژگیهای خطوط مستقیم متفاوت است. برای مثال، خطوط موازیِ روی یک صفحه هیچگاه به هم نمیرسند، اما برای ژئودزیکهای روی سطح زمین چنین نیست؛ مثلاً خطوط طول جغرافیایی در استوا موازیاند، اما در قطبها به هم میرسند.
بررسی میدان گرانشی[ویرایش]
برای اینکه اثر گرانشی یک جرم را بررسی کنیم از چیزی که فیزیکپیشهها به آن ذرهٔ آزمون میگویند استفاده میکنیم: ذراتی که از حضور میدان تأثیر میپذیرند اما خود به قدری کوچک و ناچیزند که میتوانیم از اثر گرانشیشان صرفنظر کنیم.
در غیاب میدانهای گرانشی و سایر نیروهای خارجی، ذرهٔ آزمون روی خطی مستقیم و با سرعت ثابت حرکت میکند. به بیانِ فضازمان، این معادل است با اینکه بگوییم ذرهٔ آزمون در امتداد جهانخطی مستقیم در فضازمان حرکت میکند. در حضور گرانش، ساختارِ هندسهٔ فضازمان، نااقلیدسی یا همان خمیدهاست، و در فضازمان خمیده جهانخطهای مستقیم وجود ندارند. به جای آن، ذرات آزمون در امتداد خطوطی که ژئودزیک نامیده میشوند حرکت میکنند. خطوطی که مستقیمترین خطوطِ ممکناند.
بهطور مشابه، جهانخطهای ذراتِ آزمونِ در حالِ سقوطِ آزاد، ژئودزیکهایی در فضازمان هستند، یعنی مستقیمترین خطوط ممکن در فضازمان. اما بین آنها و خطوط واقعاً مستقیم در فضازمانِ بدونِ میدانِ گرانشی در نسبیت خاص (هندسهٔ تخت یا اقلیدسی)، تفاوت اساسی وجود دارد. در نسبیت خاص، ژئودزیکهای موازی، موازی باقی میمانند. در میدان گرانشی با توجه به وجود اثرات کشندی، این مسئله در حالت کلی درست نیست. برای مثال اگر دو جسم که در ابتدا نسبت به هم ساکناند را در میدان گرانشی زمین رها کنیم، با سقوط و نزدیک شدن به مرکز جرم زمین، به هم نزدیکتر و نزدیکتر میشوند.[۲۷][۲۸]
اشیایی که در زندگی روزمره با آنها سروکار داریم (خودروها ٬خانهها ٬کوهها و…)، در مقایسه با سیارات و دیگر اجسام آسمانی جرم ناچیزی دارند. هنگام بررسی حرکت این اجسام کوچک، قوانین حاکم بر ذرات آزمون صادق هستند. به خصوص برای منحرف کردن یک ذرهٔ آزمون از مسیر ژئودزیکاش باید یک نیروی خارجی به آن اعمال نمود. یک شخص که بر روی صندلی نشستهاست، سعی میکند تا ژئودزیکی را به سمت مرکز زمین دنبال کند، یعنی به سمت مرکز جرم زمین سقوط آزاد کند. اما صندلی یک نیروی خارجی به سمت بالا به او وارد میکند و از سقوط او جلوگیری مینماید. به این ترتیب توضیح تجربیات روزمره از گرانش روی سطح زمین بر اساس نسبیت عام، به صورت نیروهای خارجی رو به بالای وارد شونده (و ممانعتکننده از سقوط آزاد) است و نه به صورت جاذبهای رو به پایین از طرف زمین. این نیروهای خارجی همهٔ اجسام روی سطح زمین را از ژئودزیکهایی که در نبود نیروها دنبال میکردند منحرف میکنند.[۲۹] برای اجسامی که اثر گرانشی خودشان بر فضازمان قابل صرفنظر نیست، قوانین حرکت کمی پیچیدهتر از قوانینِ مربوط به ذرات آزمون هستند، اما اینکه فضازمان به ماده میگوید چگونه حرکت کن همواره درست است.[۳۰]
منشأهای گرانش[ویرایش]
بر اساس قانون جهانی گرانش نیوتون، نیروی گرانشی به وسیله ماده ایجاد میشود. به بیان دقیقتر، منشأ این میدان یک ویژگیِ اجسام فیزیکی به نام جِرم است. در نظریه گرانش اینشتین و نظریههای مرتبط با آن، انحنا در هر نقطه از فضازمان، ناشی از مادهای که وجود دارد است. در اینجا نیز جرم یک ویژگی اساسی برای تعیین اثرات گرانشیِ ماده است. اما در یک نظریهٔ نسبیتی از گرانش، جرم نمیتواند تنها منشأ گرانش باشد. نسبیت جرم را به انرژی و انرژی را به تکانه مربوط میکند.
همارزی جرم و انرژی، که با رابطهٔ E = mc۲ بیان میشود، شاید مشهورترین نتیجهٔ نسبیت خاص باشد. در نسبیت خاص، جرم و انرژی دو راه متفاوت برای توصیف یک کمیت فیزیکیاند. اگر یک سامانهٔ فیزیکی انرژی داشته باشد، جرم متناظر با آن را نیز دارد و برعکس. به خصوص همهٔ ویژگیهای یک جسم که با انرژی در ارتباط اند، مانند دما یا انرژی بستگیِ سامانههای فیزیکیای مانند هسته اتم یا مولکولها، در جرم آن جسم نقش دارند و در نتیجه منشأ گرانش هستند.[۳۱]
در نسبیت خاص، انرژی رابطهٔ نزدیکی با تکانه دارد. همانگونه که فضا و زمان اجزایی از موجودِ اصلی به نام فضازمان هستند، انرژی و تکانه نیز جنبههای مختلف کمیتی دیگر به نام چارتکانه هستند. در نتیجه اگر انرژی یک منشأ گرانش باشد، تکانه نیز خواهد بود. این مطلب برای کمیتهایی که بهطور مستقیم به انرژی و تکانه مربوط هستند نیز صادق است، برای مثال برای فشار داخلی و کشش. در مجموع در نسبیت عام، منشأهای گرانش عبارتند از جرم٬انرژی، فشار و کشش. اینها راههایی هستند که ماده از آن طریق به فضازمان میگوید که چگونه خمیده شود. در فرمولبندی ریاضیاتی این نظریه، همهٔ این کمیتها اجزای یک کمیت اصلی به نام تنسور ضربه-انرژی هستند.[۳۲]
معادلات اینشتین[ویرایش]
معادلات اینشتین در قلب نسبیت عام قرار دارند. این معادلات، فرمولبندی دقیقی از رابطه بین هندسهٔ فضازمان و ویژگیهای ماده به زبان ریاضیات بیان میکنند. بهطور دقیقتر، این معادلات بر اساس مفاهیم هندسه ریمانی فرمولبندی شدهاند که در آن ویژگیهای هندسیِ یک فضا (ی چندبعدی) با کمیتی به نام متریک توصیف میشود. متریک، اطلاعات لازم برای محاسبهٔ کمیتهای بنیادیِ هندسی در یک فضا مانند فاصله و زاویه را دربردارد.

یک سطح کروی مانند سطح زمین مثالی ساده است. مکان هر نقطه روی سطح میتواند با دو مختصه بیان شود: عرض جغرافیایی و طول جغرافیایی. برخلاف آنچه در مختصات دکارتی دیده میشود، تغییر در این مختصهها بین دو نقطه، همارز با فاصله آنها روی سطح نیست. همانطور که در شکل دیده میشود، برای شخصی که روی استوا ایستادهاست، تغییری ۳۰ درجهای در طول جغرافیایی به سمت غرب متناظر با فاصلهٔ به طول ۳٬۳۰۰ کیلومتر است. اما شخصی که در طول جغرافیایی ۵۵ درجه به همین مقدار طول جغرافیاییِ خود را تغییر میدهد، فاصلهای به طول ۱٬۹۰۰ کیلومتر را طی میکند؛ بنابراین این مختصهها اطلاعات کاملی را برای توصیف هندسهٔ یک سطح کروی، یا در حالت کلی، هر فضای پیچیدهتر با ابعاد بیشتر، دربر ندارند. این اطلاعات دقیقاً چیزی هستند که در تنسور متریک فشرده شدهاند: تابعی که در هر نقطه از فضازمان تعریف شدهاست و تغییر در مختصات را به تغییر در مسافت مربوط میکند. تمام کمیتهای مورد نیاز دیگر در هندسه، مانند طول هر خم یا زاویه برخورد دو منحنی میتواند از این متریک به دست آید.[۳۳]
تابع متریک و آهنگ تغییرش از نقطهای به نقطهٔ دیگر را میتوان برای تعریف کمیتی هندسی به نام تنسور ریمان استفاده کرد، که توصیفی دقیق از چگونگی انحنای فضا (یا فضازمان) در هر نقطه ارائه میکند. در نسبیت عام، متریک و تنسور انحنای ریمان کمیتهایی هستند که در هر نقطه از فضازمان تعریف میشوند. همانگونه که قبلاً گفته شد، محتوای مادهٔ فضازمان کمیت دیگری را به نام تنسور ضربه-انرژی T تعریف میکند و این اصل که «فضازمان به ماده میگوید چگونه حرکت کن و ماده به فضازمان میگوید چگونه خمیده شو» به معنای آن است که این کمیتها باید به هم مربوط شوند. اینشتین این رابطه را با ترکیب تنسور انحنای ریمان با متریک و تعریف کمیت جدیدی به نام تنسور اینشتین، G، که جنبههایی از چگونگی خمش فضازمان را دربردارد به دست آورد. معادلهٔ اینشتین بیان میکند:
یعنی، صرفنظر از ضریب ثابت ، کمیت G (که انحنا را اندازه میگیرد) با کمیت T (که محتوای ماده را دربردارد) برابر است. ثابتهای حاضر در این معادله به خوبی بیانگر نظریههای مختلفی که در ایجاد این معادله نقش داشتهاند است: G ثابت گرانش است که در گرانش نیوتونی حاضر است، c سرعت نور است که ثابت کلیدی حاضر در نسبیت خاص است، و π که از ثابتهای اساسی هندسه است.[۳۴]
معمولاً این معادله به صورت جمع، معادلات اینشتین خوانده میشود، زیرا هرکدام از کمیتهای G و T دربردارندهٔ چندین تابع از مختصاتِ فضازمان هستند و بعد از خارج نمودن معادله از حالت فشرده به چند معادله که شامل مؤلفههای این تنسورها هستند میرسیم.[۳۵] یک پاسخ برای این معادلات، یک هندسهٔ مخصوص برای فضازمان را توصیف میکند. برای مثال، متریک شوارتزشیلد هندسه اطراف یک جرم کروی و غیرچرخان مانند یک ستاره یا سیاهچاله را توصیف میکند، و متریک کر توصیفکنندهٔ یک سیاهچالهٔ چرخان است. پاسخهای دیگری هم وجود دارند، که برای مثال میتوانند امواج گرانشی را توصیف کنند یا همانند متریک فریدمان-لومتر-رابرتسون-واکر توصیفگر جهانِ در حالِ انبساط باشند. سادهترین جواب، فضای غیرخمیدهٔ مینکوفسکی است، فضازمانی که نسبیت خاص توصیف میکند.[۳۶]
آزمونهای تجربی[ویرایش]
مطابقت نتایج و پیشبینیهای یک نظریهٔ علمی با آزمایشها یکی از معیارهای مهم برای قضاوت در مورد آن نظریه است. قانون جهانی گرانش نیوتون به دلیل توصیفِ با دقت بالایش از حرکت سیارات و قمرها در منظومهٔ شمسی سالها به عنوان مدلی برای توصیف نیروی گرانش مورد پذیرش بود. با پیشرفت دقت ابزارهای اندازهگیری، اختلافهایی با نتایجی که قانون نیوتون پیشبینی کرده بود مشاهده گردید که همگی در نسبیت عام به درستی پیشبینی شدهاند. بهطور مشابه، پیشبینیهای نظریهٔ نسبیت عام باید با آزمایش بررسی شوند. اینشتین، خود سه آزمون برای این کار طراحی کرد که امروزه با نام آزمونهای کلاسیک نسبیت عام شناخته شدهاند:[۳۷]

- گرانش نیوتونی پیشبینی میکند که مداری که یک تکسیاره به دور ستارهای کاملاً کروی دنبال میکند باید یک بیضی باشد.[۳۸] نظریهٔ اینشتین منحنی پیچیدهتری را پیشبینی میکند: سیاره همانند وقتی که یک بیضی را دنبال میکرد رفتار میکند، اما بهطور همزمان، خودِ بیضی به آرامی در حال چرخش به دورِ ستاره است. در نمودار سمت راست، بیضی پیشبینی شده توسط نظریهٔ نیوتون به رنگ قرمز و نمودار پیشبینی شده توسط نظریهٔ اینشتین به رنگ آبی نشان دادهشدهاست. برای سیارهای که به دور خورشید میچرخد این اختلاف با نظریهٔ نیوتونی، تغییر غیرعادی حضیض خورشیدی نامیده میشود. اولین بار این پدیده در سال ۱۸۵۹ برای سیارهٔ تیر مشاهده شد. دقیقترین دادههای به دست آمده از مدارهای تیر و سایر سیارهها تا به امروز، بین سالهای ۱۹۶۶ و ۱۹۹۰ و با استفاده از رادیو تلسکوپها به دست آمدند. نسبیت عام این اثر را برای مدار سیارههایی که با دقت بسیار اندازهگیری شدهاند به درستی پیشبینی میکند.[۳۹](زمین، زهره و تیر)
- طبق نسبیت عام، نور هنگام حرکت در یک میدان گرانشی، در خط مستقیم سیر نمیکند. بلکه مسیر آن توسط اجسام سنگین خم میشود. بهطور خاص، نور ستارگان هنگام گذر از کنار خورشید منحرف میشود، بهطوریکه در موقعیت ظاهری ستارگان در آسمان شب، ۱٫۷۵ ثانیهٔ قوسی تفاوت ایجاد میکند. (یک ثانیه قوسی برابر ۱/۳۶۰۰ درجه است) در چارچوب گرانش نیوتونی، با یک ابتکار میتوان خم شدن نور را نتیجه گرفت که نتیجهٔ آن خم شدن نور به میزان نیمی از عدد یاد شدهاست.[۴۰] این پیشبینیها را میتوان با مشاهدهٔ نور ستارگانی که نزدیک به خورشید دیدهمیشوند، هنگام یک خورشیدگرفتگی آزمود. در همین راستا، گروهی تحقیقاتی به رهبری آرتور استنلی ادینگتون در سال ۱۹۱۹، طی خورشیدگرفتگی ۲۹ مه ۱۹۱۹ در غرب آفریقا، درستیِ پیشبینی نظریهٔ اینشتین و نادرستی پیشبینیِ نیوتونی را تأیید کرد. نتایج ادینگتون چندان دقیق نبودند، مشاهدات بَعدی از خم شدن نور گسیلشده از اختروشهای دوردست توسط خورشید، با بهرهگیری از روشهای بسیار دقیق ستارهشناسی رادیویی، نتایج اینشتین را با دقت بسیار بالاتری تأیید کردند. (اولین این مشاهدات در سال ۱۹۶۷ انجام گرفت و آخرین آنها تاکنون مربوط به سال ۲۰۰۴ بودهاست)[۴۱]
- انتقال به سرخ گرانشی، نخستین بار در آزمایشگاه و توسط پوند و ربکا اندازهگیری شد. همچنین در اندازهگیریهای اخترفیزیکی نیز، به خصوص در مورد نور گسیل شده از کوتوله سفید شباهنگ (Sirius B) مشاهده و اندازهگیری شدهاست. برخی اثرات مرتبط، نظیر اتساع زمان گرانشی نیز بررسی شدهاند. برای مثال، اتساع زمان گرانشی با بردن ساعتهای اتمی به ارتفاعهای ۱۰ تا ۱۰ها هزار کیلومتری از سطح دریا، آزموده شدهاست. (نخستین بار توسط هافل و کیتینگ در سال ۱۹۷۱ و دقیقترین بار تا به امروز توسط کاوشگر گرانش A در سال ۱۹۷۶)[۴۲]
از این آزمونها، تنها اختلاف مدار سیارهٔ تیر با پیشبینی نظریه نیوتونی، قبل از انتشار نظریه نسبیت عام در ۱۹۱۶ شناخته شدهبودند. تأیید تجربی بقیهٔ این پیشبینیها، به خصوص اندازهگیری خمشدن نور توسط خورشید در سال ۱۹۱۹، به سرعت اعتباری جهانی به اینشتین بخشید.[۴۳] این آزمونهای تجربی، موجب بهکارگیری نظریه نسبیت عام به جای نظریه نیوتونی و نیز جایگزینهای ارائه شده برای آن گردید.
از آزمونهای جدیدترِ نسبیت عام میتوان به اندازهگیریِ دقیقِ اثر شاپیرو یا تأخیرِ زمانیِ گرانشی برایِ نور اشاره کرد که آخرین بار در سال ۲۰۰۲ توسط کاوشگر فضایی کاسینی-هویگنس انجام گرفت. دستهای از این آزمونها بر روی اثرات پیشبینی شده توسط نسبیت عام برای ژیروسکوپی که در فضا حرکت میکند تمرکز میکنند. بررسی یکی از این اثرها، اثر ژئودزیکی، توسط آزمایش فاصله سنجی لیزری ماه (اندازهگیری دقیق مدار ماه) انجام شدهاست. مورد دیگری که به اجرام چرخان مربوط است، کشش چارچوب(به انگلیسی: Frame Dragging) نام دارد. اثرات ژئودزیکی و کشش چارچوب، توسط آزمایش ماهوارهای کاوشگر گرانش B، پرتاب شده در ۲۰۰۴، بررسی شدند. تا دسامبر ۲۰۰۸، نتیجه، با دقتِ در محدودهٔ به ترتیب ۰٫۵ درصد و ۱۵ درصد، پیشبینیهای نسبیت عام را تأیید میکرد.[۴۴]
در منظومهٔ شمسی، براساس استانداردهای کیهانی، گرانش ضعیف است. به دلیل اینکه تفاوت نظریهٔ نیوتونی با نظریهٔ اینشتین در میدانهای گرانشی قوی بهتر آشکار میشود، فیزیکپیشهها همواره مشتاق بودهاند تا اثرات نسبیتی را در شرایطی که گرانش قوی است بیازمایند. این مسئله به کمک مشاهدات دقیق از تپاخترهای دوتایی ممکن گردیدهاست. در این سامانههای ستارهای، دو ستاره نوترونی بسیار فشرده به دور هم میچرخند. حداقل یکی از آنها یک تپاختر است - موجودی فضایی که پرتوهای شدیدی از امواج رادیویی گسیل میکند. این شعاعها در فواصل زمانی بسیار منظم به سمت زمین میآیند، همانگونه که چرخش یک فانوس دریایی از دور همانند یک چراغ چشمکزن به نظر میرسد، و میتواند به صورت مجموعهای از پالسهای با دورهٔ منظم مشاهده گردد. نسبیت عام انحرافهایی از دورهٔ منظم این پالسهای رادیویی پیشبینی میکند. برای مثال، وقتی که امواج رادیویی گسیل شده از یکی از ستارههای نوترونی از نزدیکی ستارهٔ نوترونی دیگر میگذرند، باید توسط میدان گرانشی آن ستاره منحرف شوند. الگوهای مشاهده شده برای این پالسها بهطور چشمگیری با پیشبینیهای نسبیت عام مطابقت دارد.[۴۵]
دستهای از مشاهدات به یکی از کاربردهای عملی بسیار مفید، یعنی سامانه ماهوارهای ناوبری جهانی مربوط هستند، مانند سامانه موقعیتیاب جهانی (GPS) که هم برای موقعیتیابی دقیق و همزمانسنجی استفاده میشود. این سامانهها بر اساس دو دسته از ساعتهای اتمی کار میکنند: ساعتهای روی ماهوارههای در مدار زمین و ساعتهای مرجع مستقر روی زمین. نسبیت عام پیشبینی میکند که آهنگ جلو رفتن این دو ساعت، باید به مقدار اندکی با هم متفاوت باشد. - به دلیل حرکت متفاوت آنها (پیشبینی شده توسط نسبیت خاص) و نیز موقعیت متفاوتشان در میدان گرانشی زمین. برای کسب اطمینان از دقت سامانه، یا زمان نشاندادهشده توسط ساعتهای ماهوارهها را در یک ضریب تصحیحِ نسبیتی ضرب میکنند یا همان ضریب را در روند نهاییِ محاسبهٔ زمان منظور میکنند. در مقابل، آزمونهای بسیار دقیق سنجش درستیِ این سامانه (به خصوص اندازهگیریهای بسیار دقیقی که بخشی از تعریف ساعت هماهنگ جهانی را تشکیل میدهند) خود تأییدی بر درستی نتایج نسبیتی هستند.[۴۶]
تعداد دیگری از آزمونها، درستی نسخههای گوناگونِ اصل همارزی را میآزمایند. به بیان صریح، همهٔ اندازهگیریهای اتساع زمان گرانشی آزمونهایی برای نسخهٔ ضعیف اصل همارزی و نه خود نسبیت عام هستند. تا به امروز نسبیت عام تمامی آزمونها را با موفقیت پشتسر گذاشتهاست.[۴۷]
کاربردهای اخترفیزیکی[ویرایش]
مدلهای براساس نسبیت عام، در اخترفیزیک نقش مهمی بازی میکنند، و موفقیت این مدلها میتواند آزمونی برای درستی نسبیت عام نیز تلقی گردد.
همگرایی گرانشی[ویرایش]

از آنجایی که مسیر نور در یک میدان گرانشی خمیده میگردد، ممکن است نورِ یک جسمِ دور از چند مسیر مختلف به ناظر برسد. برای مثال نور یک جسم بسیار دور مانند یک اختروش میتواند هنگام گذر از یک سمت یک کهکشان، به طرفِ ناظر زمینی منحرف شود و در همین حال نورِ گذرنده از سویِ دیگرِ کهکشان نیز همینطور منحرف شود و از جهتی کمی متفاوت به همان ناظر برسد. در نتیجه، ناظر یک جسم آسمانی را در دو نقطهٔ مجزا در آسمان مشاهده میکند. این پدیده شبیه به منحرف شدن نور در عدسیهایِ نوریِ همگرا است و از این رو آن را همگرایی گرانشی نامیدهاند.[۴۸]
نجوم مشاهداتی از این اثراتِ همگرایی برای بررسیِ جسمِ همگراکننده بهره میگیرد. حتی در شرایطی که شیء مورد نظر بهطور مستقیم قابل مشاهده نیست، شکل تصویرِ همگرا شده اطلاعاتی در مورد توزیع جرمِ شیء، که مسئول چگونگی منحرف ساختن نور توسط آن است به دست میدهد. به خصوص، همگرایی گرانشی ابزاری مهم برای بررسی چگونگی توزیع ماده تاریک است، مادهای که نوری از خود گسیل نمیکند و تنها توسط آثار گرانشیاش قابلِ شناسایی است. یک مورد جالب دیگر مشاهدات در مقیاس بزرگ هستند، که در آن اجسام همگراکننده در قسمت بزرگی از جهان مشاهدهپذیر پراکنده شدهاند و میتوان از آنها برای کسب اطلاعات در مورد ویژگیهای جهان در مقیاس بزرگ و تحول کیهان بهره برد.[۴۹]
امواج گرانشی[ویرایش]
همانطور که در قسمتهای پیشین گذشت، نظریهٔ نسبیت عام، فضای صُلب و مطلق نیوتونی را با فضازمان دینامیکی و قابل انعطاف جایگزین میکند. یکی از پیشبینیهای جالب این نظریه، وجود امواج گرانشی است. همانند امواج صوتی که حاصل انقباض و انبساط متناوب هوا هستند، امواج گرانشی نیز اعوجاجهایی در هندسهٔ فضازمانند که با سرعت نور منتشر میشوند و میتوان آنها را به عنوان موجی در فضازمان دانست.[۵۰]
میتوان گفت هر وضعیتی که در آن اجرام به سمت یکدیگر شتاب میگیرند منجر به تولید امواج گرانشی میشود. اما بیشتر این امواج به قدری ضعیفاند که قادر به شناسایی آنها نیستیم. منابعی که گمان میرود میتوانند امواجی با انرژی کافی برای شناسایی شدن تولید کنند چنیناند: سامانهٔ متشکل از دو ستارهٔ نوترونی در حال چرخش به دور یکدیگر، ستارهٔ نوترونی گردنده به دور یک سیاهچاله، یا دو سیاهچاله چرخان به دور یکدیگر. سیاهچالهها که در قسمت آینده به آنها خواهیم پرداخت، اجرامی بسیار فشرده هستند و همین ویژگی، این دوتاییها را به نامزدهای اصلی تولید امواج گرانشی پرانرژی تبدیل میکند. علاوه بر اینها، ابرنواخترها نیز که انفجارهای عظیم ستارههای در حال مرگ هستند، منابع پرانرژی این امواج بهشمار میروند.[۵۱]
بهطور غیرمستقیم، اثرات امواج گرانشی در مشاهدات برخی ستارههای دوتایی دیده شدهاند. این زوج ستارهها به دور یکدیگر میگردند و در همین حال کمکم انرژی خود را با گسیل امواج گرانشی از دست میدهند. برای ستارههای با جرم معمولی مانند خورشید ما، این انرژی به قدری ناچیز است که قابل شناسایی نیست، با این حال این اثر در سال ۱۹۷۴ در یک تپاختر دوتایی به نام پیاسآر بی۱۹۱۳+۱۶ مشاهده گردید. در چنین سامانهای یکی از ستارههای چرخنده یک تپاختر است. این مسئله دو نتیجه مفید به دنبال دارد: شدت گسیل امواج گرانشی از یک تپاختر که جسمی بسیار چگال (شناخته شده به نام ستاره نوترونی) است بسیار قویتر از ستارههای معمولی است. همچنین، یک تپاختر، شعاع باریکی از تابش الکترومغناطیسی از قطبهای مغناطیسی خود گسیل میکند. با چرخش تپاختر، این شعاعِ نوری، زمین را جاروب میکند و این تابش به صورت قطاری از پالسهای رادیویی با دورهٔ منظم دیده میشود، درست مانند فانوس دریایی دیده شده از کشتیها در دریا. الگوی تابشی پالسهای گسیل شده از تپاخترها بسیار منظم بوده و به اعوجاج فضازمان در همسایگی نزدیک خود (مثلاً در اثر وجود امواج گرانشی) بسیار حساس است. با گذشت زمان و گسیل امواج گرانشی، انرژی سامانهٔ دوتایی کاهش یافته، شعاع چرخش کوچکتر میشود و سرعت چرخش آنها به دور یکدیگر افزایش مییابد. با استفاده از دورهٔ پالسهای گسیل شده از تپاختر میتوان به مدار و سرعت چرخش دوتایی به دور یکدیگر پیبرد و میزان انرژی از دست رفته را محاسبه نمود.[۵۱]
برای سامانهٔ دوتایی PSR۱۹۱۳+۱، نتایج مشاهدهشده دقیقاً منطبق با پیشبینی نسبیت عام مبنی بر کاهش انرژی بر اثر گسیل امواج گرانشی بودهاست. کشفکنندگان PSR۱۹۱۳+۱۶، راسل هالس و جوزف تیلور، جایزه نوبل فیزیک در سال ۱۹۹۳ را از آن خود کردند. بعد از آن، چند تپاختر دوتایی دیگر نیز یافته شد. مفیدترین این دوتاییها آنهایی هستند که هردو ستاره تپاختر باشند، این دوتاییها امکان انجام آزمونهای بسیار دقیق نسبیت عام را فراهم میکنند.[۵۲]
به منظور آشکارسازی مستقیم این امواج تا به امروز چند آشکارساز زمینی امواج گرانشی راهاندازی شده و در حال کار هستند،[۵۳] و ساخت یک آشکارساز فضایی (LISA) نیز در حال دنبالشدن است. (ابتدا یک مأموریت پیشرو (راهیاب LISA) در سال ۲۰۱۵ انجام گرفت)[۵۴] در ۱۷ مارس ۲۰۱۴ دانشمندان در مرکز اخترفیزیک هاروارد-اسمیتسونین طی مشاهداتی به نتایجی که تاییدکننده نتایج گرانش کوانتومی، مهبانگ و انبساط کیهان از طریق امواج گرانشی بود دست یافتند،[۵۵] اما نتیجه این آزمایش نیز مشاهدهٔ مستقیم ـ به معنای اندازهگیری یک نوسان در فضازمان ـ به حساب نمیآید.[۶]
مشاهدهٔ امواج گرانشی در سال ۲۰۱۶[ویرایش]
در ۱۱ فوریه ۲۰۱۶ پژوهشگران در LIGO موفق به مشاهده مستقیم امواج گرانشی برای نخستین بار شدند.[۵] موج مشاهده شده ناشی از ترکیب دو سیاهچاله با جرمهای تقریبی ۳۶ و ۲۹ برابر جرم خورشید، و در فاصله تقریبی ۴۱۰ مگاپارسک (حدود ۱/۳ میلیارد سال نوری) از زمین بود.[۴] موج گرانشی ناشی از تبدیل جرمی معادل با سه برابر جرم خورشید به انرژی در هنگام ترکیب دو سیاهچاله با یکدیگر بود. این اولین مشاهده از ترکیب دو سیاهچاله با یکدیگر نیز به حساب میآید.
میتوان از مشاهدهٔ مستقیم امواج گرانشی برای کسب اطلاعات در مورد اجسامِ فشرده مانند ستارههای نوترونی و سیاهچالهها کمک گرفت و نیز در حالت اولیه جهان پس از گذشت کسری از ثانیه از مهبانگ، کاوش کرد.[۵۶][۵۷]
سیاهچالهها[ویرایش]
سیاهچاله نامیست که به دستهای از پاسخهای معادلات اینشتین دادهشدهاست. از نظر تاریخی، سیاهچالهها ابتدا در جریان تلاش برای یافتن پاسخ معادلات اینشتین پیشبینی شدند. هنگامیکه جرم در یک ناحیهٔ به اندازهٔ کافی فشرده از فضا متمرکز شود، نسبیت عام شکلگیری یک سیاهچاله را پیشبینی میکند. در صورت ورود هرچیز حتی نور به یک فاصله معین از (مرکز) یک سیاهچاله، امکان فرار از آن وجود ندارد. این فاصله افق رویداد نامیده شدهاست.[۵۸]
برخی از انواعِ سیاهچالهها، مرحلهٔ پایانیِ تحول ستارگان پرجرم هستند. پس از تبدیل شدن همهٔ هیدروژن ستاره به هلیوم و بعد به عناصر سنگینتر بر اثر فرایند گداخت هستهای درون ستاره، در صورتی که جرم ستاره بیش از ۱۰ تا ۲۵ برابر جرم خورشید باشد،[۵۹] ستاره به درون خود فرو میریزد و نیروهای دافعه بین ذرات زیراتمی نیز نمیتوانند این رمبش را متوقف کنند. در پایان، در صورتی که جرم ستاره نوترونی حاصل بیش از ۲ تا ۳ برابر جرم خورشید باشد[۶۰] باقیمانده ستاره به یک سیاهچاله تبدیل خواهد شد. جرم سیاهچالههایی که از این طریق تشکیل میشوند بین پنج تا چند ده برابر جرم خورشید است. از طرفی، راه دیگری نیز برای شکلگیری سیاهچالههای بسیار پرجرمتر وجود دارد. این سیاهچالهها که سیاهچالههای کلانجرم نامیده شدهاند، از رمبش گرانشی یک خوشهٔ ستارهای بسیار بزرگ ایجاد میشوند. این سیاهچالهها میتوانند جرمی از مرتبهٔ هزاران یا میلیاردها برابر خورشید داشته باشند. گمان میرود که که در مرکز هر کهکشان، یک سیاهچاله از این نوع موجود باشد. برای مثال سیاهچاله قرار گرفته در مرکز کهکشان راه شیری دارای جرمی در حدود ۴٫۳ میلیون برابر جرم خورشید است.[۶۱] این سیاهچالهها نقشی کلیدی در مدلهای فعلی شکلگیری کهکشانها در میلیاردها سال گذشته ایفا میکنند.[۶۲][۶۳]
سقوط ماده در یک سیاهچاله، فرایندی است که بازده گسیل انرژی به صورت تابش در آن بسیار بالاست. یک توده گاز در حال سقوط در یک سیاهچاله از فاصله دور، حدود ۱۰ درصد از جرم-انرژی خود را به صورت تابش گسیل میکند. این عدد حدود ۱۰ تا ۲۰ برابر بیشتر از نسبت انرژی آزاد شده بر واحد جرم برای فرایند گداخت هستهای است.[۵۸] سقوط ماده در سیاهچالهها فرایندی است که مسئول بسیاری از پدیدههای نجومی تلقی میشود. مثالهای مهم و بااهمیت در نظر ستارهشناسان عبارتند از اختروشها و دیگر انواع هسته کهکشانی فعال. در شرایط خاصی، مادهٔ سقوطکننده و تجمعکننده در اطراف سیاهچاله میتواند به ایجاد جت بینجامد، که در آن، شعاعهای ماده با سرعتهایی نزدیک به سرعت نور به فضای اطراف پرتاب میشوند.[۶۴]
سیاهچالهها چند ویژگی دارند که آنها را به امیدبخشترین نامزدهای تولیدِ امواج گرانشی بدل کردهاست. یکی آن است که سیاهچالهها فشردهترین اجرامی هستند که میتوانند به عنوان عضوی از یک دوتایی به دورِ یکدیگر بچرخند: امواج گرانشی گسیل شده از چنین سامانهای بسیار نیرومند خواهد بود. دلیل دیگر از قضیههایی که با نام قضیهٔ یکتایی سیاهچالهها شناخته شده هستند نتیجه میشود: با گذر زمان، ویژگیهایی که سیاهچالههای مختلف را فارغ از شکل اولیهشان از هم متمایز میکند کمتر و کمتر میشوند، برای مثال، پس از گذشت زمانی دراز از رمبش یک جرم مکعبیشکل، نتیجه یک سیاهچالهٔ مکعبی نخواهد بود، بلکه سیاهچالهٔ حاصل با سیاهچالهای که از رمبش جرمی کرویشکل حاصل شده یکسان خواهد بود. تنها یک تفاوت در این فرایند وجود دارد: هنگامِ گذارِ سیاهچالهِ حاصل از جرمِ مکعبی به سیاهچالهای حاصل از جرمی کروی، امواج گرانشی گسیل میشود.[۶۵]
کیهانشناسی[ویرایش]
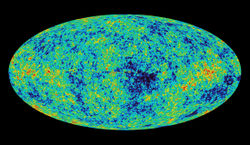
یکی از مهمترین جنبههای نسبیت عام آن است که میتوان آن را به گیتی به عنوان یک کُل اعمال کرد. نکتهٔ کلیدی این است که به نظر میرسد جهان ما بر اساس قواعد بسیار سادهای شکل گرفتهاست. همهٔ مشاهدات فعلی نشان میدهند که بهطور متوسط، ساختار کیهان باید صرفنظر از مکان ناظر و جهت مشاهده، یکسان باشد. جهان بهطور تقریبی، همگن و همسانگرد است. چنین جهانهای به نسبت سادهای را میتوان با پاسخهای سادهای از معادلات اینشتین توصیف کرد. مدلهای کیهانشناختی فعلی براساس این پاسخهای سادهٔ نسبیت عام و ترکیب آن با نظریههای توصیفکنندهٔ ویژگیهای محتوای مادهی جهان، یعنی ترمودینامیک، فیزیک هستهای و فیزیک ذرات بنا شدهاند.
براساس این مدلها، جهان فعلی ما از یک حالت بسیار چگال و با دمای بالا (طی مهبانگ) در حدود ۱۴ میلیارد سال پیش پدید آمدهاست و همچنان در حال انبساط است. مهبانگ به معنای ایجاد جهان از یک حالت تکین، و نه به معنای انفجار ماده در فضازمان موجود از پیش است. توضیح تکینگی موجود در مهبانگ نیاز به یک نظریه کوانتومی از گرانش دارد که هنوز تحقق نیافتهاست. در قسمتهای بعد به این موضوع پرداخته شدهاست.[۶۶][۶۷]
میتوان معادلات اینشتین را با افزودن یک جمله که ثابت کیهانشناسی نامیده میشود تعمیم داد. در حضور این جمله، فضای خلأ، خود منشأ جاذبه یا دافعهٔ گرانشی خواهد بود. نخستین بار اینشتین این جمله را در مقالهٔ پیشگامانهٔ خود در کیهانشناسی، با دلیلی بسیار خاص مطرح کرد: طبق تصورات فعلی کیهانشناختی، جهان ایستا است و افزودن این جمله برای ساخت مدلی ایستا از عالم بر اساس نسبیت عام لازم است. هنگامی که مشخص گردید که جهان در حال انبساط (و غیرایستا) است، اینشتین به سرعت این جملهٔ اضافی را حذف نمود. اما، از سال ۱۹۹۸ به بعد، شواهدی نجومی به دستآمدهاند و هنوز در حال گسترش هستند که نشان میدهند انبساط جهان در حال شتابگیری است، بهگونهای که یا حضور یک ثابت کیهانشناختی را لازم میدارد، یا وجود انرژی تاریک را با ویژگیهایی خاص که همهٔ جهان را فراگرفتهاست، پیشنهاد میدهد.[۶۸]
پژوهشهای جدید[ویرایش]
نسبیت عام در فراهم آوردن چارچوبی برای ساختن مدلهایی دقیق که محدودهٔ وسیعی از پدیدههای فیزیکی را توجیه میکنند بسیار موفق ظاهر شدهاست. از طرف دیگر، پرسشهای مطرح زیادی وجود دارند و به خصوص، خود نظریه به عنوان یک کل تقریباً بهطور قطعی ناقص است.[۶۹]
برخلاف سایر نظریههای جدید برای برهمکنشهای بنیادی، نسبیت عام یک نظریهٔ کلاسیک است: این نظریه، شامل اثراتِ فیزیکِ کوانتومی نمیشود و نمیتواند در ابعاد بسیار کوچک ـ حوزهٔ کارکرد مکانیک کوانتومی ـ پاسخهای صحیحی ارائه دهد. جستجوهای فعلی برای یافتن معادلات کوانتومی نسبیت عام، به دنبال پاسخگویی به یکی از مهمترین پرسشهای پاسخدادهنشدهٔ فعلی هستند. در دهههای اخیر رهیافتهای گوناگونی برای ساختن نظریهای کوانتومی از گرانش بررسی شدهاند، اما از بین آنها دو نظریه موفق به دستیابی به یک توصیف ریاضیاتی کامل از ویژگیهای کوانتومی گرانش شدهاند: نظریه ریسمان و گرانش کوانتومی حلقه(به انگلیسی: Loop Quantum Gravity).[۷۰]
گرانش کوانتومی حلقه تلاش میکند تا با بهکارگیری مفاهیم فضا و زمان از نسبیت عام در نظریه میدان کوانتومی به این هدف دست یابد. این نظریه به توصیفی گسسته مانند و دانهای از فضا منجر میشود. به بیان دقیقتر، در این نظریه فضا دارای ساختاری شبکهمانند است و کمترین فاصله معنادار، برابر با یک طول پلانک است؛ یعنی این نظریه بیان میکند که فضا نیز همانند ماده ساختاری اتمی (دانهای) دارد.[۷۰]
نظریهٔ ریسمان درصدد ارائهٔ یک نظریهٔ همهچیز، دربرگیرنده همهٔ نیروهای بنیادی است و گرانش کوانتومی نیز جزئی از آن است. در این نظریه، ذرات نقطهای در فیزیک ذرات با ریسمانهای یک بعدی جایگزین شدهاند؛ فقط یک نوع ریسمان وجود دارد و همهٔ ذرات بنیادی از حالتهای نوسانی مختلف این ریسمانها به وجود میآیند. در چارچوب این نظریه، توصیفی کوانتومی از گرانش بهطور طبیعی قابل دستیابی است. در عین حال، این دستآوردها وجود شش یا هفت بعد اضافه بر آنچه در نسبیت عام وجود دارد را در این نظریه تحمیل میکند.[۷۱]
با وجود پیشرفتهای اخیر، این نظریهها هنوز دارای مشکلاتی هستند. به خصوص، شواهد آزمایشگاهی برای تأیید یا رد نظریههای موجود وجود ندارد. چرا که این پدیدهها در مقیاس انرژی در نزدیکی مقیاس پلانک رخ مینمایند و از این رو در آزمایشهای فعلی قابل دستیابی نیستند. این موضوع گرانش کوانتومی را به یک موضوع صرفاً نظری تبدیل کردهاست.[۷۲]
انتظار میرود که این نظریهٔ کوانتومی از گرانش بتواند برخی مشکلات نسبیت عام مانند تکینگیهای فضازمان را حل کند و از این طریق به پرسشهایی نظیر «درون سیاهچاله چه میگذرد؟» یا «در نخستین لحظات پس از مهبانگ چه گذشتهاست» پاسخ دهد. در این تکینگیها، ویژگیهای فضازمان بدرفتار میشود و پیشبینیِ نسبیت عام در آن نقطه نادرست خواهد بود. همچنین، قضیههای تکینگیای مطرح شدهاند که بیان میکنند که در صورت برقراری قوانین نسبیت عام بدون اصلاح کوانتومی، چنین تکینگیهایی باید در جهان وجود داشته باشند.
تلاشهای دیگر برای اصلاح نسبیت عام ٬در چارچوب کیهانشناسی انجام میشود. در مدلهای جدید کیهانشناختی، بخش اعظم انرژی جهان به صورتیست که تاکنون بهطور مستقیم مشاهده نشدهاست، یعنی به صورت انرژی تاریک و ماده تاریک. تلاشهایی برای از بین بردن نیاز به وجود چنین شکلهایی از ماده و انرژی ٬از طریقِ اصلاحِ معادلاتِ حاکم بر گرانش و دینامیکِ انبساط جهان انجام گرفتهاند برای مثال، دینامیک نیوتونی اصلاحشده.[۷۳] اما این نظریات مشکلات زیادی به همراه دارند و به خصوص حتی با فرض درستی آنها، شواهد دیگری مبنی بر وجود مادهٔ تاریک در دست است.[۷۴]
گذشته از چالشهای مربوط به اثرات کوانتومی و کیهانشناسی، پژوهش در نسبیت عام زمینهای بسیار غنی برای کاوشهای بیشتر است: نسبیتدانهای ریاضیاتی، طبیعت تکینگیها و ویژگیها بنیادی معادلات اینشتین را بررسی میکنند[۷۵]; شبیهسازیهای رایانهای بزرگی از فضازمانهای خاص در حال انجام است[۷۶] و تلاش برای آشکارسازی مستقیم امواج گرانشی نیز هنوز ادامه دارد.[۷۷] با گذشت بیش از ۹۰ سال از انتشار نسبیت عام، پژوهش در رابطه با این نظریه از همیشه گستردهتر شدهاست.[۷۸]
جستارهای وابسته[ویرایش]
پانویس[ویرایش]
- ↑ "General relativit". Encyclopaedia Britannica (به انگلیسی). 24 September 2018. Archived from the original on 11 July 2018. Retrieved 23 April 2019.
- ↑ وستفال، تکوین علم جدید، ۲۵۱. را ببینید.
- ↑ برای مشاهده برخی مثالها وستفال، تکوین علم جدید، ۲۴۷. را ببینید
- ↑ ۴٫۰ ۴٫۱ «Observation of Gravitational Waves from a Binary Black Hole Merger». American Physical Society. بایگانیشده از اصلی در ۱۱ فوریه ۲۰۱۶.
- ↑ ۵٫۰ ۵٫۱ «Gravitational Waves Are the Ringing of Spacetime». American Physical Society. فوریه ۱۱, ۲۰۱۶. بایگانیشده از اصلی در ۱۱ فوریه ۲۰۱۶.
- ↑ ۶٫۰ ۶٫۱ «Gravitational waves discovery: 'We have a first tantalising glimpse of the cosmic birth pangs'». بایگانیشده از اصلی در ۲۹ آوریل ۲۰۱۴.
- ↑ در (Franklin 2012) به چگونگی ناسازگاری نسبیت خاص با گرانش نیوتونی و نتایج آن پرداخته شدهاست.
- ↑ این روند در (Renn 2005، صفحه ۱۱۰ (و جلوتر))، در فصلهای ۹ تا ۱۵ (Pais 1982) و در (Janssen 2005) دنبال شدهاست. خلاصهای از گرانش نیوتونی را میتوان در (Schutz 2003، فصلهای ۲–۴) یافت. گرانش نیوتونی پیش از ۱۹۰۷ نیز توجه اینشتین را به خود جلب کردهبود، اما تلاشهای جدی برای آشتی دادن آن با نسبیت خاص به همان سال برمیگردد.
- ↑ برای ارائهای ساده، (Pössel 2005) را ببینید. همچنین، این مسئله در فصل ۲ (Wheeler 1990) نیز به دقت توصیف شدهاست.
- ↑ هرچند اصل همارزی امروزه نیز به عنوان بخشی از نظریه نسبیت عام ارائه میشود، تفاوتهایی بین دیدگاه جدید با مفهوم اصلی اینشتین وجود دارد مثلاً (Norton 1985) را ببینید.
- ↑ برای مشاهدهٔ این بیان از اصل همارزی، قسمت ۱۴٫۱ کتاب (Morin 2007) را ببینید.
- ↑ (Janssen 2005، p. 64f). مطالب این قسمت را خود انیشتین در بخش XX کتاب غیر تخصصی خود، Einstein ۱۹۶۱ آوردهاست. با پیروی از ایدههایی که ارنست ماخ مطرح کردهاست اینشتین نیروی گریز از مرکز و مشابههای گرانشی آنها را نیز بررسی گرده بود. صفحات ۴۸ تا ۶۲ از (Stachel 1989) را ببینید.
- ↑ اینشتین در قسمت XX از Einstein ۱۹۶۱ این مطلب را توضیح میدهد:او جسمی را در حالت آویزان از یک طناب از سقف اتاقی بر روی موشکی در حال شتابگیری در نظر گرفت:از درون اتاق چنینی به نظر میرسد که گرانش جسم را به پایین میکشد، اما از بیرون موشک مشاهده میشود که طناب، در حال انتقال نیروی موشک به جسم است.
- ↑ بهطور دقیقتر، محاسبات اینشتین، که در فصل ۱۱b از (Pais 1982) آمدهاند، از اصل همارزی و نیز نتایج نظریهٔ نسبیت خاص در مورد انتشار نور و در مورد ناظرهای شتابدار (با در نظر گرفتن چارچوبی لَخت در هر لحظه، برای هر ناظر شتابدار) استفاده میکنند.
- ↑ این اثر را میتوان مستقیماً از نسبیت خاص نتیجه گرفت، هم با بررسی موقعیت همارز دو ناظر در یک موشک شتابدار یا با در نظر گرفتن یک آسانسور سقوطکننده. در هر دو وضعیت، برای انتقال بسامد، توصیفی یکسان وجود دارد:یک انتقال دوپلری بین چارچوبهای لَخت معین. برای به دیدن چگونگی به دست آوردن این نتیجه، (Harrison 2002) را ببینید.
- ↑ فصل ۱۲ (Mermin 2005) را ببینید.
- ↑ (Ehlers و Rindler 1997); برای ارائهای ساده و غیرتخصصی (Pössel 2010) را ببینید.
- ↑ اثرات کشندی نیروی گرانش به زبان ساده در (Penrose 2002، صفحات ۲۶۴–۲۶۶) مطرح شدهاند.
- ↑ این اثر و سایر اثرات کشندی، در (Wheeler 1990، صفحات ۸۳–۹۱) بررسی شدهاند.
- ↑ نیروهای کشندی و تعبیر هندسی آنها در فصل ۵ (Wheeler 1990) توضیح داده شدهاند. این مرحله از توسعهٔ نظریه از لحاظ تاریخی در (Pais 1982، section 12b) دنبال شدهاست.
- ↑ برای شرحی مقدماتی از مفهوم فضازمان، نخستین بخش فصل دوم (Thorne 1994) و نیز (Greene 2004، p. ۴۷–۶۱) را ببینید. بررسی کاملتر و نسبتاً مقدماتی را میتوان در (Mermin 2005) و (Wheeler 1990، فصلهای ۸ و ۹) یافت.
- ↑ برای شرح جالبی از فضازمان خمیده، (Wheeler 1990، فصلهای ۸ و ۹) را ببینید.
- ↑ تلاش اینشتین برای یافتن شکل صحیح معادلاتِ میدان، در فصلهای ۱۳ تا ۱۵ (Pais 1982) دنبال شدهاست.
- ↑ مثلاً صفحهٔ xi از (Wheeler 1990) را ببینید.
- ↑ در صفحات ۱۶۶ تا ۱۷۰ در (Geroch 1978) با بیانی ساده و غیرریاضیاتی به این موضوع پرداخته شدهاست.
- ↑ Yan-Bin Jia (اکتبر ۲۵, ۲۰۱۲). «Geodesics» (PDF). بایگانیشده از اصلی (PDF) در ۳ اوت ۲۰۱۳. دریافتشده در اوت ۳, ۲۰۱۳.
- ↑ «Geometric Gravity». بایگانیشده از اصلی در ۵ اوت ۲۰۱۳.
- ↑ شرحی مفصل و در عین حال ساده از هندسهدیفرانسیل را میتوان در (Geroch 1978) یافت.
- ↑ فصل ۱۰ (Wheeler 1990) را ببینید.
- ↑ در حقیقت، در صورت شروع از شکل کامل و نهایی نظریه، میتوان از معادلات اینشتین، معادلات حرکت اجسام در حالت کلی را یافت، اما به دست آوردن این معادلات با استفاده از معادلات ذرات آزمون کار دشواری است؛ مثلاً (Poisson 2004) را ببینید.
- ↑ توضیحی ساده از همارزی جرم-انرژی را میتوان در قسمتهای ۳٫۸ و ۳٫۹ (Giulini 2005) یافت.
- ↑ فصلِ ۶ (Wheeler 1990) را ببینید.
- ↑ برای یک تعریف جزئی تر (و البته غیررسمیتر از تعریف کتابهای درسی) از متریک، فصل ۱۴٫۴ (Penrose 2004) را ببینید.
- ↑ فصل ۴ از (Carroll 1997) را ببینید.
- ↑ به معنای هندسی معادلات اینشتین در فصلهای ۷ و ۸ (Wheeler 1990) پرداخته شدهاست. جعبهٔ ۲٫۶ را نیز ببینید. مقدمهای با استفاده از ریاضیات بسیار ساده در فصل ۱۹ (Schutz 2003) آورده شدهاست.
- ↑ مهمترین پاسخها در هر کتاب در اینجا آورده شدهاند. برای یک خلاصهٔ (فنی) از وضعیت فعلی (Friedrich 2005) را ببینید.
- ↑ «Tests of general relativity, classical». EinsteinOnline. بایگانیشده از اصلی در ۱۳ مارس ۲۰۱۹. دریافتشده در اوت ۳, ۲۰۱۳.
- ↑ «why aren't the planets' orbits circular?». NASA. بایگانیشده از اصلی در ۴ اوت ۲۰۱۳.
- ↑ بهطور دقیقتر اینها اندازهگیریهای تداخل خط پایه بسیار طولانی موقعیت سیارهای هستند. فصل ۵ (Will 1993) و قسمت ۳٫۵ (Will 2006) را ببینید.
- ↑ محاسبه میزان خم شدن نور با استفاده از نظریه نیوتونی و نیز نسبیت عام، در (Soares 2009) آورده شدهاست.
- ↑ برای مشاهدهٔ اندازهگیریهای تاریخی، صفحات ۱۸۲ تا ۱۸۷ از (Hartl 2005)، صفحات ۱۷۸ تا ۱۸۱ از (Kennefick 2005) و (Kennefick 2007) را ببینید. محاسبات اصلی سالدنر در چارچوب نظریهٔ نیوتون در (Soldner 1804) آمدهاست. برای دقیقترین اندازهگیریها تا به امروز (Bertotti 2005) را ببینید.
- ↑ (Kennefick 2005) و فصل ۳ (Will 1993)را ببینید. برای اندازهگیریهای بر اساس ستارهٔ شباهنگ، (Trimble و Barstow 2007) را ببینید.
- ↑ (Pais 1982),سیاره تیر در صفحات ۲۵۳–۲۵۴, به شهرت رسیدن اینشتین در قسمتهای ۱۶b و ۱۶c.
- ↑ Everitt, C.W.F؛ Parkinson, B.W. «نتایج کاوشگر گرانش B - گزارش نهایی ناسا» (PDF). بایگانیشده از اصلی (PDF) در ۳ ژوئن ۲۰۱۳. دریافتشده در ۲۰۱۳-۰۳-۰۷.
- ↑ صفحات ۳۳ تا ۵۴ در (Kramer 2004)
- ↑ شرح سادهای از اثرات نسبیتی در سامانه موقعیتیابی جهانی را میتوان در (Ashby 2002) یافت. جزئیات در (Ashby 2003) آورده شدهاند.
- ↑ این مطالب در (Will 1993) به زبان ساده آورده شدهاند. شرحی تخصصیتر و بهروزتر در (Will 2006) آمدهاست.
- ↑ هندسهٔ چنین موقعیتهایی در فصل ۲۳ (Schutz 2003) بررسی شدهاست.
- ↑ آشنایی با همگرایی گرانشی و کابردهای آن را میتوان در (Newbury 1997) و (Lochner 2007) یافت.
- ↑ "Gravitational Waves" (به انگلیسی). Max Planck Institute for Gravitational Physics. Archived from the original on 15 May 2019. Retrieved 15 May 2019.
- ↑ ۵۱٫۰ ۵۱٫۱ «Making waves». Max Planck Institute for Gravitational Physics. بایگانیشده از اصلی در ۵ سپتامبر ۲۰۱۳. دریافتشده در اوت ۴, ۲۰۱۳.
- ↑ صفحات ۳۱۷ تا ۳۲۱ در (Schutz 2003، صفحات ۳۱۷–۳۲۱)و صفحات ۷۰ تا ۸۶ در (Bartusiak 2000) .
- ↑ در مورد آشکارسازهای زمینی نظیر LIGO و GEO600، (Krishnan 2010) را ببینید.
- ↑ در مورد آشکارسازهای فضایی LISA و eLISA, (Aufmuth 2010) را ببینید.
- ↑ «First Direct Evidence of Cosmic Inflation». بایگانیشده از اصلی در ۲۹ آوریل ۲۰۱۴.
- ↑ «On the Edge: Gravitational Waves». NASA. اوت ۲۰۰۳. بایگانیشده از اصلی در ۲ اوت ۲۰۱۳. دریافتشده در اوت ۸, ۲۰۱۳.
- ↑ پژوهشهای فعلی در رابطه با امواج گرانشی، در (Bartusiak 2000) و (Collins 2004) آورده شدهاست.
- ↑ ۵۸٫۰ ۵۸٫۱ «Questions and Answers about Black Holes». بایگانیشده از اصلی در ۳ اوت ۲۰۱۳. دریافتشده در اوت ۴, ۲۰۱۳.
- ↑ Schild and Maeder, “The initial mass limit for neutron star and black hole formation”.
- ↑ Margalit and Metzger, “Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817”; Bombaci, “The maximum mass of a neutron star”.
- ↑ Gillessen, “MONITORING STELLAR ORBITS AROUND THE MASSIVE BLACK HOLE IN THE GALACTIC CENTER”.
- ↑ برای مشاهدهٔ تاریخچهای از فیزیک سیاهچالهها از ابتدا تا کنون، نوشتار بسیار خواندنی (Thorne 1994)، به خصوص قسمت پیشگفتار و فصل ۴ را ببینید. برای بحث بهروزی از نقش سیاهچالهها در شکلگیری ساختار (کهکشانها)، (Springel 2005) را ببینید. خلاصهٔ مختصری را میتوان در مقالهٔ (Gnedin 2005) یافت.
- ↑ «Gravitational Collapse». بایگانیشده از اصلی در ۳ اوت ۲۰۱۳. دریافتشده در اوت ۴, ۲۰۱۳.
- ↑ فصل ۸ (Sparke و Gallagher 2007) و صفحات ۵۲ تا ۵۷ از (Disney 1998) را ببینید. بحث جامع دیگری که ریاضیات چندانی هم ندارد، در (Fabian 1999) آمدهاست.
- ↑ مقدمهٔ سادهای بر قضیههای بکتاییِ سیاهچالهها را میتوان در (Chrusciel 2006) و (Thorne 1994، صفحات ۲۷۲–۲۸۶) یافت.
- ↑ فصل آخر (Carroll 1997) را ببینید.
- ↑ اطلاعات دقیقتر را میتوان در آموزش کیهانشناسیِ نِد رایت و پرسشوپاسخها، (Wright 2007) یافت. یک مقدمهای بسیار خواندنی بر موضوع، (Hogan 1999) است. (Berry 1989) با استفاده از ریاضیات در سطح کارشناسی و اجتناب از ابزارهای ریاضی پیشرفته شرحی جامعتر ارائه میکند.
- ↑ (Einstein 1917) مقالهٔ اصلی اینشتین است. توصیفی مناسب از پیشرفتهای جدید را میتوان در (Cowen 2001) و (Caldwell 2004) یافت.
- ↑ صفحات ۵۲–۵۹ و ۹۸ تا ۱۲۲ (Maddox 1998) و بخش ۳۴٫۱ و فصل ۳۰ در (Penrose 2004) را ببینید.
- ↑ ۷۰٫۰ ۷۰٫۱ (Rovelli 2003)
- ↑ «Superstrings and universal harmony». Max Planck Institute for Gravitational Physics. بایگانیشده از اصلی در ۱۴ ژوئن ۲۰۱۸. دریافتشده در ۱۱ سپتامبر ۲۰۱۳.
- ↑ «Relativity and Quantum». Max Planck Institute for Gravitational Physics. بایگانیشده از اصلی در ۲ ژوئیه ۲۰۱۸. دریافتشده در ۱۱ سپتامبر ۲۰۱۳.
- ↑ برای جرم تاریک، صفحات ۳۰ تا ۳۷ از (Milgrom 2002) را ببینید. برای انرژی تاریک، به (Caldwell 2004) مراجعه کنید.
- ↑ یک شاهد مهم بر این ادعا، یک خوشهٔ کهکشانی به نام خوشهٔ فشنگ است که در این گزارش ناسا آمدهاست: «ماده در خوشهٔ فشنگ». ناسا. بایگانیشده از روی نسخه اصلی در ۱۰ آوریل ۲۰۱۹. دریافتشده در ۲۰ ژوئیه ۲۰۱۳.
- ↑ (Friedrich 2005) را ببینید.
- ↑ مروری بر مسائل گوناگون و روشهای برخورد با آنها در (Lehner 2002) آمدهاست.
- ↑ برای توصیفی از تلاشها (تا سال ۲۰۰۰) قسمت ۳٫۵ از (Bartusiak 2000) را ببینید. اطلاعات بهروز را در وبگاه آشکارسازها مانند GEO 600 بایگانیشده در ۱۸ فوریه ۲۰۰۷ توسط Wayback Machine و LIGO میتوان یافت.
- ↑ یک مرجع مناسب و مقدماتی برای آگاهی از پژوهشهای امروزه در نسبیت، مجله الکترونیکی Living Reviews in Relativity بایگانیشده در ۲۷ دسامبر ۲۰۱۶ توسط Wayback Machine است.
منابع[ویرایش]
- وستفال، ریچارد (۱۳۷۹)، تکوین علم جدید، ترجمهٔ آذرنگ، عبدالحسین؛ رضایی، رضا، طرح نو، شابک ۹۷۸۹۶۴۵۶۲۵۷۴۸
- Ashby, Neil (2002), "Relativity and the Global Positioning System", Physics Today (به انگلیسی), vol. 55, p. 41–47, Bibcode:2002PhT....55e..41A, doi:10.1063/1.1485583, archived from the original (PDF) on 3 June 2013
- Ashby, Neil (2003), "Relativity in the Global Positioning System", Living Reviews in Relativity (به انگلیسی), vol. 6, archived from the original on 3 June 2013, retrieved 2007-07-06
- Bartusiak, Marcia (2000), Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time (به انگلیسی), Berkley
- Berry, Michael V. (1989), Principles of Cosmology and Gravitation (به انگلیسی) (2nd ed.), Institute of Physics Publishing
- Penrose, Roger (2002), The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics (به انگلیسی), Oxford University Press
- Morin, David (2007), Introduction to Classical Mechanics (به انگلیسی), Cambridge University Press
- Bertotti, Bruno (2005), "The Cassini Experiment: Investigating the Nature of Gravity", in Renn, Jürgen (ed.), One hundred authors for Einstein (به انگلیسی), Wiley-VCH, p. 402–405
- Collins, Harry (2004), Gravity's Shadow: The Search for Gravitational Waves (به انگلیسی), Perseus
- Caldwell, Robert R. (2004), "Dark Energy", Physics World (به انگلیسی), vol. 17, p. 37–42, doi:10.1088/2058-7058/17/5/36, archived from the original on 10 April 2019
- Chrusciel, Piotr (2006), "How many different kinds of black hole are there?", How many different kinds of black hole are there (به انگلیسی), archived from the original on 3 June 2013, retrieved 2007-07-15
- Cowen, Ron (2001), "A Dark Force in the Universe", Science News (به انگلیسی), Society for Science &, vol. 159, p. 218, doi:10.2307/3981642, JSTOR 3981642
- Disney, Michael (1998), "A New Look at Quasars", Scientific American (به انگلیسی), vol. 6, p. 52–57, doi:10.1038/scientificamerican0698-52
- Ehlers, Jürgen; Rindler, Wolfgang (1997), "Local and Global Light Bending in Einstein's and other Gravitational Theories", General Relativity and Gravitation (به انگلیسی), vol. 29, p. 519–529, Bibcode:1997GReGr..29..519E, doi:10.1023/A:1018843001842
- Einstein, Albert (1917), "Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie", Sitzungsberichte der Preußischen Akademie der Wissenschaften (به انگلیسی), p. 142
- Einstein, Albert (1961), Relativity. The special and general theory (به انگلیسی), Crown Publishers, archived from the original on 3 June 2013
- Friedrich, Helmut (2005), "?'Is general relativity 'essentially understood", Annalen Phys. (به انگلیسی), vol. 15, p. 84–108, arXiv:gr-qc/0508016, Bibcode:2006AnP...518...84F, doi:10.1002/andp.200510173
- Geroch, Robert (1978), General relativity from A to B (به انگلیسی), University of Chicago Press
- Giulini, Domenico (2005), Special relativity. A first encounter (به انگلیسی), Oxford University Press
- Gnedin, Nickolay Y. (2005), "Digitizing the Universe", Nature (به انگلیسی), vol. 435, p. 572–573, Bibcode:2005Natur.435..572G, doi:10.1038/435572a, PMID 15931201
- Greene, Brian (1999), The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory (به انگلیسی), Vintage
- Greene, Brian (2004), "The Fabric of the Cosmos. Space, Time, and the Texture of Reality", The fabric of the cosmos: space (به انگلیسی), A. A. Knopf, Bibcode:2004fcst.book.....G
- Harrison, David M. (2002), A Non-mathematical Proof of Gravitational Time Dilation (به انگلیسی), archived from the original (PDF) on 3 June 2013, retrieved 2007-05-06
- Soares, Domingos (2009), Newtonian gravitational deflection of light revisited (به انگلیسی), arXiv:physics/0508030v4, archived from the original (PDF) on 2 July 2018, retrieved 2013-08-05
- Franklin, Joel (2012), Newtonian Gravity and Special Relativity (به انگلیسی), archived from the original (PDF) on 5 August 2013, retrieved 2013-08-05
- Hartl, Gerhard (2005), "The Confirmation of the General Theory of Relativity by the British Eclipse Expedition of 1919", in Renn, Jürgen (ed.), One hundred authors for Einstein (به انگلیسی), Wiley-VCH, p. 182–187
- Hogan, Craig J. (1999), The Little Book of the Big Bang. A Cosmic Primer (به انگلیسی), Springer
- Janssen, Michel (2005), "Of pots and holes: Einstein's bumpy road to general relativity", Ann. Phys. (Leipzig) (به انگلیسی), vol. 14, p. 58–85, Bibcode:2005AnP...517S..58J, doi:10.1002/andp.200410130, archived from the original (PDF) on 3 June 2013
- Kennefick, Daniel (2005), "Astronomers Test General Relativity: Light-bending and the Solar Redshift", in Renn, Jürgen (ed.), One hundred authors for Einstein (به انگلیسی), Wiley-VCH, p. 178–181
- Kennefick, Daniel (2007), "Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition", Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005 (به انگلیسی), vol. 0709, p. 685, arXiv:0709.0685, Bibcode:2007arXiv0709.0685K
- Kramer, Michael (2004), "Millisecond Pulsars as Tools of Fundamental Physics", in Karshenboim, S. G.; Peik, E. (eds.), Astrophysics, Clocks and Fundamental Constants (Lecture Notes in Physics Vol. 648) (به انگلیسی), Springer, p. 33–54
- Lehner, Luis (2002), "NUMERICAL RELATIVITY: STATUS AND PROSPECTS", General Relativity and Gravitation - Proceedings of the 16th International Conference (به انگلیسی), p. 210, arXiv:gr-qc/0202055, Bibcode:2002grg..conf..210L, doi:10.1142/9789812776556_0010
- Lochner, Jim, ed. (2007), "Gravitational Lensing", Imagine the Universe website (به انگلیسی), NASA GSFC, archived from the original on 3 June 2013, retrieved 2007-06-12
- Maddox, John (1998), What Remains To Be Discovered (به انگلیسی), Macmillan
- Mermin, N. David (2005), It's About Time. Understanding Einstein's Relativity (به انگلیسی), Princeton University Press
- Milgrom, Mordehai (2002), "Does dark matter really exist?", Scientific American (به انگلیسی), vol. 287, p. 30–37, doi:10.1038/scientificamerican0802-42, archived from the original on 3 June 2013
- Norton, John D. (1985), "What was Einstein's principle of equivalence?", Studies in History and Philosophy of Science (به انگلیسی), vol. 16, p. 203–246, doi:10.1016/0039-3681(85)90002-0, archived from the original (PDF) on 3 June 2013, retrieved 2007-06-11
- Newbury, Pete (1997), Gravitational lensing webpages (به انگلیسی), archived from the original on 3 June 2013, retrieved 2007-06-12
- Nieto, Michael Martin (2006), "The quest to understand the Pioneer anomaly", EurophysicsNews (به انگلیسی), vol. 37, p. 30–34, archived from the original (PDF) on 3 June 2013
- Pais, Abraham (1982), 'Subtle is the Lord...' The Science and life of Albert Einstein (به انگلیسی), Oxford University Press
- Penrose, Roger (2004), The Road to Reality (به انگلیسی), A. A. Knopf
- Carroll, Sean (1997), Lecture Notes on General Relativity (به انگلیسی), arXiv:gr-qc/9712019v1, archived from the original on 2 July 2018, retrieved 2013-08-04
- Krishnan, B. (2010), Listening posts around the globe (به انگلیسی), archived from the original on 4 August 2013, retrieved 2013-08-04
- Rovelli, Carlo (2003), Loop Quantum Gravity (PDF) (به انگلیسی), retrieved 2013-09-11
- Krishnan, B. (2010), Listening posts around the globe (به انگلیسی), archived from the original on 4 August 2013, retrieved 2013-08-04
- Krishnan, B. (2010), Listening posts around the globe (به انگلیسی), archived from the original on 4 August 2013, retrieved 2013-08-04
- Aufmuth, P. (2010), eLISA - Hunting waves in space (به انگلیسی), archived from the original on 4 August 2013, retrieved 2013-08-04
- Pössel, M. (2005), The elevator, the rocket, and gravity: the equivalence principle (به انگلیسی), archived from the original on 8 August 2013, retrieved 2013-08-03
- Pössel, M. (2010), The equivalence principle and the deflection of light (به انگلیسی), archived from the original on 3 August 2013, retrieved 2013-08-03
- Poisson, Eric (2004), "The Motion of Point Particles in Curved Spacetime", Living Rev. Relativity (به انگلیسی), vol. 7, archived from the original on 3 June 2013, retrieved 2007-06-13
- Renn, Jürgen, ed. (2005), Albert Einstein– Chief Engineer of the Universe: Einstein's Life and Work in Context (به انگلیسی), Berlin: Wiley-VCH
- Fabian, Andrew (1999), "Active galactic nuclei", PNAS (به انگلیسی), vol. 96, doi:10.1073/pnas.96.9.4749, archived from the original (PDF) on 3 August 2013
- Schutz, Bernard F. (2003), Gravity from the ground up (به انگلیسی), Cambridge University Press
- Smolin, Lee (2001), Three roads to quantum gravity (به انگلیسی), Basic
- Soldner, Johann Georg von (1804), , Berliner Astronomisches Jahrbuch (به انگلیسی), p. 161–172.
- Sparke, Linda S.; Gallagher, John S. (2007), Galaxies in the universe– An introduction (به انگلیسی), Cambridge University Press
- Springel, Volker (2005), "Simulations of the formation, evolution and clustering of galaxies and quasars", Nature (به انگلیسی), vol. 435, p. 629–636, arXiv:astro-ph/0504097, Bibcode:2005Natur.435..629S, doi:10.1038/nature03597, PMID 15931216
- Stachel, John (1989), "The Rigidly Rotating Disk as the 'Missing Link in the History of General Relativity'", in Howard, D.; Stachel, J. (eds.), Einstein and the History of General Relativity (Einstein Studies, Vol. 1) (به انگلیسی), Birkhäuser, p. 48–62
- Thorne, Kip (1994), Black Holes and Time Warps: Einstein's Outrageous Legacy (به انگلیسی), W W Norton & Company
- Trimble, Virginia; Barstow, Martin (2007), "Gravitational redshift and White Dwarf stars", Gravitational redshift and White Dwarf stars (به انگلیسی), archived from the original on 3 June 2013, retrieved 2007-06-13
- Wheeler, John A. (1990), A Journey Into Gravity and Spacetime, Scientific American Library (به انگلیسی), San Francisco: W. H. Freeman
- Will, Clifford M. (1993), Was Einstein Right? (به انگلیسی), Oxford University Press
- Will, Clifford M. (2006), "The Confrontation between General Relativity and Experiment", Living Rev. Relativity (به انگلیسی), vol. 9, archived from the original on 3 June 2013, retrieved 2007-06-12
- Wright, Ned (2007), Cosmology tutorial and FAQ (به انگلیسی), University of California at Los Angeles, archived from the original on 3 June 2013, retrieved 2007-06-12
- Schild, H.; Maeder, A. (1985), "The initial mass limit for neutron star and black hole formation", Astronomy and Astrophysics (به انگلیسی), vol. 143, Bibcode:1985A&A...143L...7S
- Margalit, Ben; Metzger, Brian D. (2017), "Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817", The Astrophysical Journal Letters (به انگلیسی), vol. 850, Bibcode:2017ApJ...850L..19M
- Bombaci, I. (1996), "The maximum mass of a neutron star", Astronomy and Astrophysics (به انگلیسی), vol. 305, p. 871, Bibcode:1996A&A...305..871B
- Gillessen, S. (2009), "MONITORING STELLAR ORBITS AROUND THE MASSIVE BLACK HOLE IN THE GALACTIC CENTER", The Astrophysical Journal (به انگلیسی), vol. 692, Bibcode:1996A&A...305..871B
پیوند به بیرون[ویرایش]
| در ویکیانبار پروندههایی دربارهٔ آشنایی با نسبیت عام موجود است. |
- اینشتین آنلاین. وبگاهی با مقالاتی در مورد جنبههای گوناگون فیزیک نسبیتی با در نظر داشتن مخاطب عام.



