نورشناسی غیرخطی
اپتیک غیرخطی (NLO) شاخهای از اپتیک است که رفتار نور در ماده غیرخطی را توصیف میکند، که در این ماده چگالی قطبش دیالکتریک P بهطور غیرخطی به میدان الکتریکی E نور پاسخ میدهد. معمولاً این غیرخطیت فقط در شدتهای نور بسیار بالا (مقادیر میدان الکتریکی قابل مقایسه با میدانهای الکتریکی درون اتمی، نوعاً ۱۰۸ ولت بر متر) مانند شدت لیزرهای پالسی مشاهده شدهاست. انتظار میرود که خلأ فراتر از حد شوینگر غیرخطی شود. در اپتیک غیرخطی، اصل برهمنهی دیگر اعتبار ندارد.
اپتیک غیرخطی تا زمان کشف تولید هارمونیک دوم کمی بعد از اختراع اولین لیزر ناشناخته ماند.
فرایندهای غیرخطی نوری[ویرایش]
اپتیک غیرخطی گروهی از پدیدهها را موجب میشود:
فرایندهای تطبیق فرکانسی[ویرایش]
- تولید هارمونیک دوم (SHG)، یا دوبرابرسازی فرکانس، تولید نور با فرکانس دوبرابر (نصف طولموج)، با از بین رفتن دو فوتون، یک فوتون با فرکانس دو برابر به وجود میآید.
- تولید هارمونیک سوم (THG)، تولید نور با فرکانس سه برابر (یک سوم طولموج)، با از بین رفتن سه فوتون، یک فوتون با فرکانس سه برابر به وجود میآید.
- تولید هارمونیک بالا (HHG)، تولید نور با فرکانسهای بسیار بزرگتر از فرکانس اصلی (نوعاً ۱۰۰ تا ۱۰۰۰ برابر بزرگتر)
- تولید فرکانس جمع (SFG)، تولید نور با فرکانسی که جمع دو فرکانس دیگر است (SHG یک حالت خاص آن است)
- تولید فرکانس تفاضل (DFG)، تولید نور با فرکانسی که اختلاف بین دو فرکانس دیگر است.
- تقویت پارامتری نور (OPA)، تقویت ورودی سیگنال در حضور موج پمپ با فرکانس بالاتر، بهطور همزمان تولید موج ایدلر (میتوان بهعنوان DFG در نظر گرفت)
- نوسان پارامتری نور (OPO)، تولید موج سیگنال و ایدلر با استفاده از تقویتکننده پارامتریک در تشدیدگر (بدون ورود سیگنال)
- تولید پارامتری نور (OPG)، مانند نوسان پارامتری اما بدون تشدیدگر، درعوض استفاده از بهره بالا
- تبدیل پایین پارامتری خود به خودی (SPDC)، تقویت نوسانات خلأ در ناحیه بهره کم
- یکسوسازی نور (OR)، تولید میدانهای نوری شبه استاتیک
- برهمکنش نور- ماده غیرخطی با الکترونهای آزاد و پلاسما
سایر فرایندهای غیرخطی[ویرایش]
- اثر کر نوری، شدت وابسته به ضریب شکست (اثر )
- خود کانونی، نتیجه اثر کر نوری (و امکان غیرخطبت مرتبه بالاتر) ناشی از تغییرات فضایی شدت که ایجادکننده تغییرات فضایی در ضریب شکست است.
- قفل شدگی مد لنز کر (KLM)، استفاده از خود کانونی به عنوان سازوکار لیزر مد قفلشده
- خودمدولاسیون فازی (SPM)، نتیجه اثر کر نوری (و امکان غیرخطیت مرتبه بالاتر) ناشی از تغییرات زمانی در شدت که ایجادکننده تغییرات زمانی در ضریب شکست است.
- سالیتونهای نوری، حالت پایدار برای هر پالس نوری (سالیتون زمانی) یا مد فضایی (سالیتون فضایی) که در زمان انتشار به علت تعادل بین پراش و اثر کر تغییر نمیکند (مانند خودمدولاسیون فازی برای سالیتونهای زمانی و خودکانونی برای سالیتونهای فضایی).
- مدولاسیون عرضی فاز (XPM)
- ترکیبسازی چهارموج (FWM)، همچنین میتواند از سایر غیرخطیتها ناشی شود
- تولید موج با قطبش عرضی (XPW)، اثر که موجب تولید موج با بردار قطبش عمود بر موج ورودی میشود
- ناپایداری مدولاسیونی
- تقویت رامان
- مزدوج فاز نوری * پراکنش بریلوئن برنگیخته، برهمکنش فوتونها با فونونهای صوتی
- جذب چند فوتونی، جذب همزمان دو یا چند فوتون، انتقال انرژی به یک الکترون
- فوتویونیزاسیون چندگانه، خروج تقریباً همزمان چندین الکترون توسط یک فوتون
- آشفتگی در سیستمهای نوری
فرایندهای مرتبط[ویرایش]
در این فرایندها، ماده دارای پاسخ خطی به نور است، اما خواص ماده متأثر از علل دیگر است:
- اثر پاکلز، ضریب شکست توسط یک میدان الکتریکی ایستا تحت تأثیر قرار میگیرد؛ مورد استفاده در مدولاتورهای الکترونوری؛
- اکوستو- اپتیک، ضریب شکست توسط امواج صوتی (فراصوت) تحت تأثیر قرار میگیرد؛ مورد استفاده در مدولاتورهای اکوستو- اپتیک؛
- پراکندگی رامان، برهمکنش فوتونها با فونونهای نوری.
فرایندهای پارامتری[ویرایش]
اثرات غیرخطی را به دو گروه کیفی متفاوت، اثرات پارامتری و غیر پارامتری، تقسیم میکنند. غیرخطیت پارامتری برهمکنشی است که در آن حالت کوانتومی مواد غیرخطی در برهمکنش با میدان نوری تغییر نمیکند. به عنوان نتیجهای از این، فرایند «آنی» است؛ بقای انرژی و تکانه در میدان نوری، ایجاد تطبیق فازی را مهم میکند؛ و وابسته به قطبش است.
تئوری[ویرایش]
پدیدههای نوری غیرخطی پارامتری و اتلاف 'آنی' (یعنی الکترونیک)، که در آن میدانهای نوری بسیار بزرگ نیستند، میتوانند به وسیله بسط سری تیلور چگالی قطبش دیالکتریک (تکانه دو قطبی در واحد حجم) (P(t در زمان t برحسب میدان الکتریکی (E(tتوصیف شوند:
اینجا، ضرایب χn پذیرفتاریهای مرتبه nام ماده هستند و حضور این چنین ترمی در حالت کلی به عنوان غیرخطیت مرتبه nام است. بهطور کلی χn تانسور مرتبه n+1 نشاندهنده ماهیت وابسته به قطبش برهمکنش پارامتری و همچنین تقارنهای (یا عدم آنها) مواد غیرخطی است.
معادله موج در مواد غیرخطی[ویرایش]
منشأیی برای مطالعه امواج الکترومغناطیس، معادله موج است. با شروع از معادلات ماکسول در فضای همسانگرد بدون بار آزاد، میتوان نشان داد که:
که PNL بخش غیرخطی چگالی قطبش است و n ضریب شکست ناشی از ترم خطی در P است.
توجه داشته باشید که معمولاً میتوان با استفاده از بردار یکانی
و قانون گاوس
برای بهدست آوردن معادله موج آشناتر
در حالت کلی، برای محیط غیرخطی قانون گاوس به صورت زیر
حتی برای ماده همسانگرد درست نمیباشد. اگرچه در صورتی که این ترم عیناً صفر نیست، اغلب بسیار کوچک است و بنابراین معمولاً با صرف نظر کردن آن، معادله موج غیرخطی استاندارد به صورت زیر بیان میشود:
غیرخطیت به عنوان فرایند ترکیب موج[ویرایش]
معادله موج غیرخطی یک معادله دیفرانسیل غیرهمگن است. حل کلی با بررسی معادلات دیفرانسیل عادی به دست میآید و میتواند با تابع گرین حل شود. بهطور فیزیکی جوابهای موج الکترومغناطیس عادی بخش همگن معادله موج به دست میآید:
و ترم غیرهمگن
به عنوان تولیدکننده یا منبع امواج الکترومغناطیس عمل میکند. یکی از نتایج، برهمکنشی غیرخطی است که انرژی در فرکانسهای مختلف را ترکیب یا کوپل میکنند که اغلب ترکیب موج نامیده میشود.
در حالت کلی مرتبه nام منجر به ترکیب موج n+1ام میشود. به عنوان مثال، اگر فقط غیرخطیت مرتبه دوم (ترکیب سه موج) را در نظر بگیریم، قطبش، P، به صورت زیر است.
اگر فرض کنیم که (E(t ترکیبی از دو رنگ در فرکانسهای ω۱ وω۲ است، میتوانیم(E(tرا به صورت بنویسیم؛ که .c.c به عنوان مزدوج مختلط است. با قرار دادن این در رابطه P داریم
که دارای مؤلفههای فرکانسی در ۲ω۱,۲ω۲, ω۱+ω۲, ω۱-ω۲ و ۰ است. این فرایندهای ترکیب سه موج به ترتیب به اثرات غیرخطی با عناوین تولید هارمونیک دوم، تولید فرکانس-جمع، تولید فرکانس-تفاضل و یکسوسازی نوری مرتبط میشوند.
توجه کنید: تقویت و تولید پارامتری نمونهای از تولید فرکانس تفاضل است، که فرکانس پایینتر یکی از دو میدان تولیدشده بسیار ضعیفتر (تقویت پارامتری) یا کاملاً غایب (تولید پامتری) است. در مورد آخر، اصل عدم قطعیت کوانتوم مکانیک فرایند را شروع میکند.
تطبیق فاز[ویرایش]
در بالا وابستگی مکانی میدانهای الکتریکی در نظر گرفته نمیشود. در شرایط عادی، میدانهای الکتریکی موجهای روندهای هستند که بهصورت زیر توصیف میشوند:
در مکان ,، با بردار موج , که سرعت نور و ضریب شکست ماده در فرکانس زاویهای است؛ بنابراین، قطبش مرتبه دوم در فرکانس زاویهای است.
در هر مکان داخل ماده غیرخطی، نوسان قطبش مرتبه دوم در فرکانس زاویهای تابش میکند و بردار موج مربوطه است. تداخل سازنده، و در نتیجه شدت بالای میدان ، اتفاق میافتد در صورتی که
معادله بالا بهعنوان شرط تطبیق فاز شناخته شدهاست. معمولاً، ترکیب سه موج در مواد کریستالی دوشکستی اتفاق میافتد (یعنی، ضریب شکست به قطبش و جهت نور عبوری بستگی دارد)، که در آن قطبش میدانها و جهت کریستال طوری انتخاب میشود که شرط تطبیق فاز ارضا شود. این روش تطبیق فاز تنظیم زاویه نامیده میشود. معمولاً یک کریستال دارای سه محور است، یکی یا دو تا از آنها دارای ضریب شکست متفاوت با بقیه آنها است (دیگری هستند). برای مثال، کریستالهای تک محوری دارای یک محور ارجح، به نام محور غیرعادی (e) هستند، در صورتیکه دوتای دیگر محورهای عادی (o) هستند (اپتیک کریستال را ببینید). چندین روش برای انتخاب قطبشها برای این نوع کریستال وجود دارد. اگر سیگنال و ایلدر دارای قطبش یکسان باشند، "تطبیق فاز نوع I" نامیده میشود، و اگر قطبش آنها عمود باشد، "تطبیق فاز نوع II" نامیده میشود. اگر چه، قراردادهای دیگری به وجود آمدهاند که مشخص میکنند هر فرکانس چه قطبشی نسبت به محور کریستال دارد. این نوعها، با قرارداد اینکه طولموج سیگنال کوچکتر از طولموج ایلدر است، به شرح زیر هستند.
| قطبش | ترتیب | ||
|---|---|---|---|
| Pump | Signal | Idler | |
| e | o | o | Type I |
| e | o | e | Type II (or IIA) |
| e | e | o | Type III (or IIB) |
| e | e | e | Type IV |
| o | o | o | Type V (or Type-0 or Zero) |
| o | o | e | Type VI (or IIB or IIIA) |
| o | e | o | Type VII (or IIA or IIIB) |
| o | e | e | Type VIII (or I) |
کریستالهای تک محوره منفی، به معنی این است که محورe کوچکتر از ضریب شکست محورهای o است، رایجترین کریستالهای غیرخطی هستند. در این نوع کریستالها، معمولاً نوع I و II تطبیق فازی روشهای مناسب هستند. در کریستالهای تک محوره مثبت، نوع VII و VIII مناسب تر است. نوع II و III معمولاً معادلند، جز مواردی که سیگنال و ایدلر جابهجا شوند، یعنی وقتی سیگنال طول موج بلندتری از ایدلر دارد. به این دلیل، گاهی اوقات آنها را IIA و IIB مینامند. شماره نوعهای V–VIII کمتر از نوعهای I و II و جایگزینهایشان رایج هستند.
یک اثر نامطلوب تنظیم زاویه این است که فرکانسهای نوری دخیل نمیتوانند نسبت به هم موازی انتشار یابند. این به علت این واقعیت است که موج غیرعادی منتشر شده در کریستال دوشکستی دارای بردار پوینتینگ است که با بردار انتشار موازی نیست. این امر منجر به walk-off پرتو میشود که راندمان تبدیل نور غیرخطی را محدود میکند. دو روش دیگر تطبیق فاز از walk-off پرتو با وادار کردن همهٔ فرکانسها به انتشار تحت زاویه ۹۰ درجه نسبت به محور نوری کریستال جلوگیری میکنند. این روشها تنظیم دمایی و شبه تطبیق فاز نامیده میشوند.
تنظیم دمایی این است که قطبش فرکانس (لیزر) پمپ عمود بر قطبش فرکانس سیگنال و ایلدر باشد. دوشکستی در بعضی از کریستالها، به ویژه در لیتیوم نئوبات بسیار وابسته به دما است. کریستال در دمای معینی برای ایجاد شرایط تطبیق فاز کنترل میشود.
روش دیگر تطبیق فاز گاوسی است. در این روش فرکانسهای دخیل دائماً همفاز با یکدیگر قفل نشدهاند، در عوض محور کریستال در فاصله منظم Λ تغییر میکند، معمولاً ۱۵ میکرومتر در طول. از این رو، این کریستالها قطبی متناوب نامیده میشوند. این باعث میشود که پاسخ قطبش کریستال همفاز با پرتو پمپ با معکوس کردن پذیرفتاری غیرخطی به عقب شیفت کند. این اجازه میدهد تا انرژی مثبت خالص از فرکانس پمپ به فرکانسهای سیگنال و ایلدر انتقال یابد. در این مورد، خود کریستال بردار موج اضافی k=۲π/λ (و بنابراین تکانه) را برای ارضا شرایط تطبیق فاز فراهم میکند. تطبیق فاز گاوسی میتواند به توریهای چیرپ شده برای پهنای باند بیشتر و برای ایجاد پالس SHG مانند آنچه در dazzler انجام شده گسترش داد. SHG پمپ و خود مدولاسیون فاز (شبیهسازی توسط فرایندهای مرتبه دوم) سیگنال و تقویت پارامتری نوری را میتوان یکپارچه کرد.
ترکیب فرکانسهای مراتب-بالاتر[ویرایش]
موارد بالا برای فرایندهای مرتبه دوم برقرار هستند. میتوان این فرایندها را به جایی که غیر صفر باشد، که در هر محیط بدون محدودیت تقارنی برقرار است، بسط داد. تولید هماهنگ سوم یک فرایند مرتبه سوم است، هرچند در کاربردهای لیزر، از آن به عنوان فرایند دو مرحلهای استفاده میشود: ابتدا فرکانس لیزر اولیه دوبرابر میشود و سپس فرکانسهای اولیه و دوبرابر شده در یک فرایند فرکانس مجموع به همدیگر اضافه میشوند. علاوه بر این اثر کر را نیز میتوان به عنوان پدیدهٔ غیرخطی مرتبه سوم معرفی نمود.
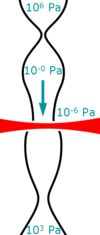
در شدتهای بالا، که منجر به غلبه مراتب بالاتر میشود، سری تیلور همگرا نمیشود و به جای آن یک مدل زمانی استفاده میشود. وقتی یک پالس لیزری شدید، که قدرت میدان الکتریکی اش قابل مقایسه با میدان کولنی اتم باشد، به اتم گاز نجیب ضربه میزند، ممکن است الکترونهای خارجی اتم یونیزه شوند. الکترون میتواند توسط میدان الکتریکی نور، ابتدا از یون دور شود، سپس با تغییر جهت میدان به طرف آن برگردد. ممکن است الکترونی که با اتم بازترکیب میشود، انرژی خودش را به شکل فوتون آزاد کند. نور گسیل شده در هر پیک میدان نوری لیزر، که به اندازه کافی شدید باشد، یک سری فلش نور آتوثانیه تولید میکند. انرژیهای فوتون تولید شده توسط این فرایند تا مرتبه هماهنگ ۸۰۰ ام تا 1300 الکترونولت بالا رود. به این فرایند تولید هماهنگی مرتبه-بالا گویند. لیزر باید قطبیده خطی باشد، تا اینکه الکترون به نزدیکی یون مادر بازگردد. تولید هماهنگهای بالا در جتهای (سلولهای) گاز نجیب و موجبرهای لوله مویین پر شده از گاز مشاهده شدهاست.
مثال کاربردهای اپتیک غیرخطی[ویرایش]
دوبرابرسازی فرکانس[ویرایش]
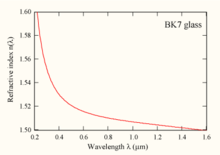
یکی از رایجترین فرایندهای ترکیب فرکانسی به کار رفته دوبرابرسازی فرکانس یا تولید هماهنگ دوم است. با این تکنیک، خروجی 1064 nm از لیزرهای Nd:YAG یا خروجی 800 nm از لیزر تیتانیوم سافایر را میتوان به ترتیب به طول موجهای 532 نانومتر (سبز) یا 400 نانومتر (بنفش) نور مرئی تبدیل کرد. عملاً، دوبرابرسازی فرکانس با قراردادن یک محیط غیرخطی در پرتوی لیزر انجام میشود. درحالیکه محیطهای غیرخطی زیادی وجود دارند، کریستالها رایجترین محیطهای غیرخطی هستند. رایجترین کریستالهای به کار رفته KDP (پتاسیم دی هیدروژن فسفات)، BBO (بتا-باریم بورات)، KTP (پتاسیم تیتانیل فسفات) و لیتیم نیوبایت هستند. این کریستالها خصوصیات مهمی از جمله دوشکستی قوی (برای دستیابی به تطبیق فازی)، داشتن تقارن خاص کریستال و البته شفاف بودن برای هر دو طول موج لیزر و نور دوبرابرشده فرکانسی و داشتن آستانه آسیب بالا، که آنها را در مقابل نور لیزرهای شدت بالا مقاوم میسازد، هستند. با این وجود مواد پلیمری ارگانیک ساخته شدند تا جانشین کریستالها شوند چون ساخت آنها آسانتر است و ولتاژ محرک و عملکرد بهتری دارند.
مزدوج فاز نوری[ویرایش]
ممکن است با استفاده از فرایندهای نوری، جهت انتشار و تغییر فاز پرتو نور دقیقاً معکوس شود. به این پرتو معکوس پرتو مزدوج گفته میشود و بنابراین این تکنیک به عنوان مزدوج فاز نوری (معکوس زمانی، معکوس جبهه موج و بازتابش نیز نامیده میشود) شناخته میشود.
میتوان این برهمکنش غیرخطی نور را مشابه فرایند هولوگرافی زمان واقعی توجیه کرد. در این مورد، پرتوهای برهمکنشی همزمان در یک ماده نوری غیرخطی برهمکنش میکنند تا یک تمام نگار متحرک (دو یا سه پرتو ورودی)، یا الگوی پراش زمان واقعی را در ماده تشکیل دهند. در زبان اپتیک غیرخطی، پرتوهای برهمکنشکننده باعث ایجاد یک قطبش غیرخطی درون ماده میشوند، که بهطور همدوس تابش میکند تا موج مزدوج فاز را تشکیل دهند.
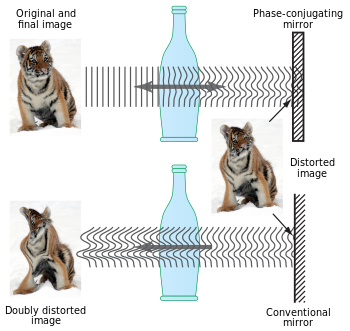
رایجترین روش برای تولید مزدوج فاز نوری استفاده از روش ترکیب چهار موج است، با این وجود ممکن است از فرایندهایی مثل پراکنش بریلوئن القایی نیز استفاده شود. وسیلهای که اثر مزدوج فاز را ایجاد میکند به عنوان آینه مزدوج فاز شناخته میشود(PMC).
برای روش ترکیب چهار موج، چهار موج (j = ۱٬۲٬۳٬۴) با میدانهای الکتریکی:
داریم که Ej دامنههای میدان الکتریکی هستند. Ξ۱ و Ξ۲ به عنوان دو موج پمپ، Ξ۳ موج سیگنال و Ξ۴ موج مزدوج تولید شده شناخته میشوند.
اگر موجهای پمپ و موج سیگنال بر محیطی با غیر صفر اعمال شوند یک میدان قطبش غیر صفر تولیدمیکند:
نتیجه تولید امواج با فرکانسهایی است که توسط ω = ±ω۱ ±ω۲ ±ω۳ به همراه امواج تولید هماهنگ سومω = ۳ω۱, ۳ω۲, ۳ω۳ارائه میشود. مانند بالا، شرط تطبیق فازی تعیین میکند که این امواج غالب باشند. با انتخاب شرایطی مانندω = ω۱ + ω۲ - ω۳ و k = k۱ + k۲ - k۳، میدان قطبش به این صورت داده میشود:
این رابطه میدان تولید شده برای پرتو مزدوج فازی، Ξ۴، است. جهت آن توسط k۴ = k۱ + k۲ - k۳ داده میشود و بنابراین اگر دو موج پمپ بهطور متقابل منتشر شوند(k۱ = -k۲)، پرتوهای سیگنال و مزدوج در جهتهای مخالف منتشر میشوند(k۴ = -k۳). این باعث خصوصیت بازتابشی اثر میشود.
علاوه بر این، میتوان نشان داد برای محیطی با ضریب شکست n و پرتویی با طول برهمکنش l، دامنه میدان الکتریکی پرتو مزدوج توسط رابطه زیر تقریب زده میشود:
که c سرعت نور است. اگر پرتوهای پمپ E۱ و E۲ موجهای تخت (انتشارمتضاد) باشند، آنگاه:
که این، دامنه موج تولیدی مزدوج مختلط دامنه پرتو سیگنال است. چون بخش مجازی دامنه شامل فاز پرتو میشود، باعث معکوسسازی خصوصیت فاز اثر میشود. توجه کنید که ثابت تناسب بین پرتوهای سیگنال و مزدوج میتواند بیشتر از ۱ باشد. این آینهای با ضریب بازتاب بیشتر از ۱۰۰٪ است، که یک بازتاب تقویتشده را ایجاد میکند. توان آن از دو موج پمپ ناشی میشود، که توسط فرایند تخلیه میشود. فرکانس موج مزدوج میتواند با موج سیگنال متفاوت باشد. اگر موجهای پمپ دارای فرکانس ω۱ = ω۲ = ω باشند و موج سیگنال از نظر فرکانسی بیشتر باشد مانند ω۳ = ω + Δω، آنگاه موج مزدوج دارای فرکانس ω۴ = ω — Δω خواهد بود. این عمل به چرخش فرکانس مشهور است.












![{\displaystyle {\begin{aligned}\mathbf {P} ^{NL}=\varepsilon _{0}\chi ^{(2)}\mathbf {E} ^{2}(t)&=\varepsilon _{0}\chi ^{(2)}[|E_{1}|^{2}e^{-i2\omega _{1}t}+|E_{2}|^{2}e^{-i2\omega _{2}t}\\&\qquad +2E_{1}E_{2}e^{-i(\omega _{1}+\omega _{2})t}\\&\qquad +2E_{1}E_{2}^{*}e^{-i(\omega _{1}-\omega _{2})t}\\&\qquad +2\left(|E_{1}|+|E_{2}|\right)e^{0}],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/833b3c79c9bf8d979e41686fa4f6a0c4f909d7ac)

















