ژیروسکوپ

از ویکی‌پدیا، دانشنامهٔ آزاد
پرش به: ناوبری، جستجو
Right
 این مقاله نیازمند تمیزکاری است. لطفاً تا جای امکان آن‌را از نظر املا، انشا، چیدمان و درستی بهتر کنید، سپس این الگو را از بالای مقاله بردارید. محتویات این مقاله ممکن است غیر قابل اعتماد و نادرست یا جانبدارانه باشد یا قوانین حقوق پدیدآورندگان را نقض کرده باشد.
Translation arrow fa.svg این نوشتار یک ترجمه از ویکی‌پدیاهای دیگر است. پيوند به سایر زبان‌ها را در سمت راست-پايين اين صفحه ببينيد.
ژیروسکوپ

ژیروسکوپ وسیله‌ای برای اندازه‌گیری و یا حفظ جهت می‌باشد که از اصل بقای تکانهٔ زاویه‌ای استفاده می‌کند.[۱] یک ژیروسکوپ مکانیکی همیشه یک چرخ یا دیسک چرخنده با محور آزاد دارد که می‌تواند در هر جهتی بایستد. این جهتگیری بسیار کمتر بر اثر گشتاور خارجی تغییر می‌کند که این به دلیل ممان زاویه‌ای بزرگ خود به همراه نرخ زیاد چرخش آن است. چون گشتاور خارجی توسط نگاه داشتن وسیله در یک حلقه کمینه می‌شود جهت آن تقریبا ثابت می‌ماند، صرفنظر از اینکه سطحی که وسیله روی آن قرار گرفته چقدر حرکت می‌کند. ژیروسکوپ‌های با تکنولوژی حالت جامد هم وجود دارند مانند ژیروسکوپ‌های حلقهٔ لیزری.

کاربردهای ژیروسکوپ شامل هدایت زمانی که قطب‌های مغناطیسی کار نمی‌کنند (مانند تلسکوپ هابل) و یا به اندازه کافی دقیق نیستند (مثل ICBM) و یا برای پایدارسازی ماشین‌های پرنده مثل هلیکوپترهای هدایت شونده توسط رادیو و یا UAVها می‌باشد. به دلیل دقت بالاتر، ژیروسکوپ‌ها همچنین در حفظ جهت در معدن کاری تونل‌ها هم به کار می‌روند.[۲]

محتویات

توصیف و نمودار [ویرایش]

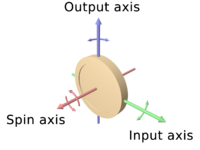
دیاگرام یک چرخ ژیروسکوپ. عکس العمل نیروها در راستای محور خروجی با رنگ آبی نشان داده شده‌است.

در وسایل و سیستم‌های مکانیکی یک ژیروسکوپ معمولی دارای ساختاری شامل یک روتور که برای چرخیدن به یک محور متصل شده‌است، ژورنال‌های روتور بر روی یک حلقه یا حلقه داخلی نصب شده، و حلقه داخلی برای نوسان بر روی یک حلقه خارجی که خود برای نوسان نسبت به یک تکیه گاه وصل شده‌است نصب شده‌است. حلقه یا حلقه خارجی همچنین برای لولا بودن به دور یک محور که بر روی صفحهٔ خودش که توسط تکیه گاه مشخص می‌شود نصب می‌گردد. حلقه خارجی یک درجه آزادی چرخش دارد و محورش هم هیچ آزادی ندارد. حلقه داخلی به طوری بر روی حلقه خارجی نصب می‌شود که بر روی یک محور در صفحه خودش که همیشه بر محور حلقه خارجی عمود است لولا می‌شود.

تصویری متحرک از یک ژیروسکوپ

محور چرخ دوار محور چرخش را تعریف می‌کند. حلقه داخلی دو درجه آزادی چرخش دارد و محورش هم یک درجه آزادی دارد. روتور برای چرخش به محوری متصل است که همیشه به محور حلقه داخلی عمود است. بنابراین روتور سه درجه آزادی چرخش دارد و محورش هم دو درجه دارد. چرخ به نیروی وارد بر محور ورودی با نیروی عکس العمل به محور خروجی پاسخ می‌دهد.

رفتار یک ژیروسکوپ می‌تواند به سادگی با توجه به رفتار چرخ جلوی دوچرخه درک می‌شود. اگر چرخ از محور عمود به سمت چپ متمایل شود لبه جلوی چرخ هم به سمت چپ می‌چرخد. به عبارت دیگر چرخش بر روی یک مورد چرخ چرخان، چرخش در محور سوم را موجب می‌شود.

یک flywheel ژیروسکوپ می‌چرخد و یا مقاومت می‌کند بسته به اینکه حلقه خارجی در ساختار آزاد یا بسته باشد. مثال‌های از وسایل با حلقه خارجی آزاد می‌تواند ژیروسکوپ‌های با مرجع جهت(attitude reference gyroscope) باشند که برای اندازه گیری زاویه در راستای سه محور مختصات (غلت و تاب و انحراف سمت) در یک فضاپیما و یا هواپیما مورد استفاده قرار می‌گیرند.

مرکز جرم چرخانه می‌تواند در یک موقعیت ثابت باشد. چرخانه به صورت همزمان توانایی چرخش به حول یک محور و نیز ارتعاش به حول دو محور دیگر را داراست و بنابراین به جز مقاومت ذاتی اش به دلیل اسپین روتور می‌تواند به طور آزادانه در هر جهتی به حول نقطهٔ ثابت بچرخد. برخی ژیروسکوپ‌ها جایگزین‌های مکانیکی برای یک یا چند عنصر به کار رفته در این ساختار دارند. برای مثال روتور می‌تواند در یک سیال معلق شود به جای اینکه به صورت لولا به یک حلقه نصب شود. یک ژیروسکوپ کنترل گشتاور (CMG) مثالی از یک وسیله با حلقه خارجی ثابت است که بر روی هواپیما با هدف تامین و یا نگهداری یک زاویهٔ وضعیت مناسب و یا جهت را با استفاده از نیروی مقاومت ژیروسکوپ استفاده می‌کند.

در برخی انواع خاص حلقه خارجی و یا معادلش می‌تواند حذف شود تا چرخانه تنها دو درجه آزادی داشته باشد. در برخی انواع مرکز جرم می‌تواند از محور نوسان فاصله داشته باشد و بنابراین مرکز جرم و مرکز تعلیق ممکن است یکی نباشد.

تاریخچه [ویرایش]

ژیروسکوپ ساخته شده توسط Léon Foucaultو ساخته شده توسط Dumoulin-Fromentدر سال 1852. موزه ملی هنرها پاریس.

اولین ژیروسکوپ شناخته شده توسط یک آلمانی به نام یوهان بوهننبرگر که اولین بار در سال ۱۸۱۷ درباره اش نوشت ساخته شده‌است. در ابتدا او آن را «ماشین» نامید.[۳][۴] ژیروسکوپ بوهننبرگر بر اساس یک کرهٔ بزرگ چرخنده ساخته شد.[۵] در سال ۱۸۳۲ والتر جانسون آمریکایی ژیروسکوپی ساخت که براساس دیسک چرخنده کار می‌کرد.[۶][۷] ریاضیدان فرانسوی پیر لاپلاس زمانی که در دانشگاه اکول پلی‌تکنیک کار می‌کرد این ماشین را به عنوان ابزار کمک آوزشی پیشنهاد کرد و به این شکل این وسیله در معرض توجهLéon Foucault قرار گرفت.[۸] در سال۱۸۵۲ Foucault که در حال انجام یک آزمایش برای دیدن چرخش زمین بود، به این وسیله نام جدید خود را داد.[۹][۱۰] اگرچه این آزمایش به دلیل وجود اصطکاک ناموفق بود. در واقع اصطکاک زمان هر دور را به ۸ تا ۱۰ دقیقه محدو می‌کرد که زمان بسیار کوتاهی برای مشاهدهٔ یک حرکت قابل توجه بود.

در سال‌های دهه ۱۹۶۰ موتورهای الکتریکی این مفهوم را امکان پذیر کردند و این به ساخته شدن اولین نمونه‌های قطب نماهای ژیروسکوپی انجامید. اولین قطب نمای ژیروسکوپی در سال ۱۹۰۸ توسط مخترع آلمانی HermannAnschutz-Kaempfe معرفی شد. کمی بعد در همان سالElmer Sperry آمریکایی طراحی خود را ادامه داد و به زودی ملت‌های دیگر هم اهمیت نظامی این اختراع را دریافتند، (در زمانی که قدرت دریایی مهمترین ابزار سنجش قدرت نظامی بود.) و صنایع ژیروسکوپ خود را ساختند. شرکت Sperry Gyroscope به زودی فعالیت خود را به ساخت پایدار کنندهای هواپیماها و کشتی‌ها هم توسعه داد و سایر سازندگان ژیروسکوپ هم به این کار پرداختند.[۱۱] در سال ۱۹۱۷ شرکت Chandler Company of Indianapolis در ایندیانا «ژیروسکوپ Chandler» را به عنوان یک اسباب بازی با یک محور و یک بند تولید کرد. این وسیله تا امروز تولیدش ادامه پیدا کرده‌است و به عنوان یک اسباب بازی کلاسیک امریکایی شناخته می‌شود.

ژیروسکوپ‌های MEMS ایده پاندول‌های Foucault را گرفته و از یک عنصر ارتعاش کننده به نامMicro Electro Mechanical System استفاده می‌کنند. ژیروسکوپ‌های بر پایهٔ MEMS اولین بار توسط System Donner Inertial SDI به طور عملی و قابل تولید ساخته شد. امروزه SDI یک تولید کنندهٔ بزرگ ژیروسکوپ‌های MEMS است.

در اولین دهه‌های قرن ۲۰ام، سایر مخترعان به صورت ناموفق تلاش کردند که از ژیروسکوپ به عنوان پایه‌ای برای جعبه سیاه سیستم‌های ترابری به وسیلهٔ ساختن یک پایهٔ پایدار که بر اساس آن اندازه گیری دقیق شتاب امکان پذیر باشد (به منظور رفع نیاز برای رویت ستارگان برای محاسبهٔ موقعیت) استفاده کنند. اصول مشابهی بعداً در ساخت سیستم‌های inertial guidance برای موشک‌های بالستیک مورد استفاده قرار گرفت.[۱۲]

ویژگی‌ها [ویرایش]

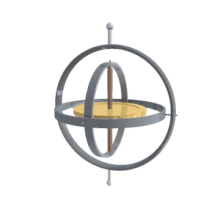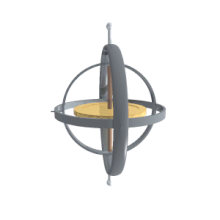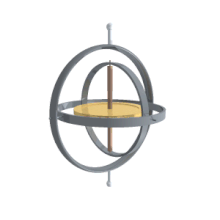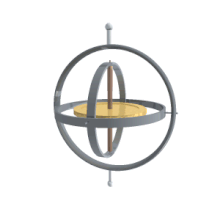
یک ژیروسکوپ در حال کار که هر سه محور آن آزاد هستند. روتور جهت محور چرخش خود را صرف نظر از جهتگیری فریم خارجی حفظ می‌کند.

یک ژیروسکوپ رفتارهایی از جمله Precession و nutation را نشان می‌دهد. ژیروسکوپ‌ها می‌توانند در ساخت قطب نماهای ژیروسکوپ که کامل کننده و یا جایگزینی برای قطب نماهای مغناطیسی در کشتی‌ها، هواپیماها، فضاپیماها و کلا وسایل حمل و نقل، برای کمک به پایداری در کشتی‌ها، تلوسکوپ فضایی هابل دوچرخه‌ها و موتورها و یا به عنوان بخشی از یک سیستم inertial guidance مورد استفاده قرار گیرد.

اثرات ژیروسکوپ‌ها در tops، بومرنگها، یویوها و powerballs مورد استفاده قرار می‌گیرد. بسیاری از وسایل چرخندهٔ دیگر مثل flywheel هم رفتار زیروسکوپی دارند اگرچه خاصیت ژیروسکوپ آنها مورد استفاده قرار نمی‌گیرند.

معادله اساسی که رفتار یک ژیروسکوپ را توصیف می‌کند به صورت زیر است:

\boldsymbol\tau={{d \mathbf{L}}\over {dt}}={{d(I\boldsymbol\omega)} \over {dt}}=I\boldsymbol\alpha

که در آن τ,Lبه ترتیب ممنتوم زاویه‌ای و گشتاور ژیروسکوپ، I ممان اینرسی، بردار ωسرعت زاویه‌ای و αشتاب زاویه‌ای آن است. از این رابطه نتیجه می‌شود که گشتاورτ که عمود بر محور چرخش و بنابراین عمود بر L وارو شود منجر به چرخشی در راستای محوری عمود بر τو Lمی‌شود. این حرکت precession نام دارد. سرعت زاویه‌ای ΩP هم توسط ضرب خارجی زیر داده می‌شود:

\boldsymbol\tau=\boldsymbol\Omega_{\mathrm{P}} \times \mathbf{L}.
Precession on a gyroscope

Precession را می‌توان با قرار دادن یک ژیروسکوپ چرخان به طوری که در یک طرف است بسته شده باشد و طرف دیگرش تقریبا آزاد باشد و محورش (بدون اصطکاک به طرف precession) بچرخد نشان داد. در این حالت ژیروسکوپ به نظر می‌رسد که بر جاذبه غلبه می‌کند و محورش افقی باقی می‌ماند. زمانی که یک طرف محور آزاد و بی تکیه گاه است و طرف دیگرش به آرامی دایره‌ای را در صفحه‌ای موازی افقی می‌پماید. این پدیده با معادله بالا توضیح داده می‌شود.

گشتاور وارد بر ژیروسکوپ از دو منبع تامین می‌شود. نیروی جاذبه که به طور عمود به سمت پایین بر مرکز جرم وارد می‌شود و یک نیروی مساوی به طرف بالا که به طرف تکیه گاه وسیله وارد می‌شود. چرخش ناشی از این گشتاور به سمت پایین نیست تا به طوری که احتمالا مورد انتظار است وسیله به زمین بخورد، در واقع بر آیند اینها عمود بر هر دو گشتاور جاذبه‌ای (افقی و عمود بر محور چرخش) و محور چرخش (افقی و به سمت بالا از محل تکیه گاه) یعنی یه دور یک محور عمودی خواهد بود که موجب می‌شود وسیله به آرامی حول نقطهٔ تکیه گاهش بچرخد. تحت یک اندازهٔ گشتاور ثابت τ سرعت تغییر جهت، ΩP به صورت معکوس با L متناسب است و نیز با اندازهٔ ممان زاویه‌ای آن:

\tau = \mathit{\Omega}_{\mathrm{P}} L \sin\theta\!

که در آن θزاویهٔ بین بردارهای Lو ΩP است. بنابراین اگر سرعت چرخش ژیروسکوپ کاهش یابد (برای مثال به دلیل اصطکاک) ممان زاویه‌ای آن کاهش پیدا می‌کند و در نتیجهٔ آن نرخ Precession آن افزایش پیدا می‌کند. این تا زمانی که وسیله دیگر قادر به سریع پیچیدن برای حمل وزن خود نیست، زمانی که Precession آن تمام شد و از تکیه گاهش می‌افتد که این اتفاق بیشتر به دلیل این است که اصطکاک مقابل Precession موجب Precession دیگری می‌شود که باعث افتادن وسیله‌است.

به صورت معمول این سه بردار گشتاور، چرخش و Precession همگی نسبت به همدیگر با توجه به قانون دست راست جهت گیری شده‌اند. برای تعیین راحت جهت اثر ژیروسکوپ به سادگی به خاطر داشته باشید که یک چرخ در حال چرخش وقتی که به گوشه می‌رود به طرف داخل به چرخش در می‌آید.

ژیروستات [ویرایش]

ژیروستات نوعی دیگر از ژیروسکوپ است. اولین ژیروستات توسط لرد کلوین(Lord Kelvin) ساخته شد تا حالت پیچیدهٔ حرکت یک حجم چرخان زمانی که تحت یک صفحهٔ افقی آزاد گذاشته شود مثل یک top spun در پیاده رو و یا یک دوچرخه یا حلقه بر روی خیابان نشان می‌دهد. این وسیله شامل یک چرخ سنگین است که در داخل یک پوشش جامد قرار گرفته است. رفتار این وسیله بر روی یک میز و یا اشکال مختلف تعلیق و یا تکیه گاه برای نمایش وضعیت‌های خاص بر خلاف قوانین معمل تعادل استاتیکی که به دلیل رفتار ژیرواستاتیکی چرخ و نامرئی داخلش وقتی که سریع بچرخد به کار می‌رود.

حق ثبت امریکا [ویرایش]

در طبقه بندی USPTO محل عمومی برای ژیروسکوپ کلاس ۷۴،Machine element or mechanism، و طبقهٔ فرعی ۵R می‌باشد. هر حجم چرخانی خواص و رفتار ژیروسکوپ دارد ولی این وسیله‌ها شامل اینکه حداقل یک محور نوسان حاضر باشد. ترکیب ژیروسکوپ با وسایل دیگر در طبقه بندی فرعی ۵٫۲۲ قرار دارند.

جستارهای وابسته [ویرایش]

جستجو در ویکی‌نَسک در ویکی‌نسک کتابی با عنوان: High School Physics/Rotational Motion وجود دارد.

مطالعات بیشتر [ویرایش]

  • Felix Klein and Arnold Sommerfeld, "Über die Theorie des Kreisels" (Tr. , About the theory of the gyroscope). Leipzig, Berlin, B.G. Teubner, 1898–1914. 4 v. illus. 25 cm.
  • Audin, M. Spinning Tops: A Course on Integrable Systems. New York: Cambridge University Press, 1996.

منابع [ویرایش]

جستجو در ویکی‌انبار در ویکی‌انبار پرونده‌هایی دربارهٔ ژیروسکوپ موجود است.
  1. ↑ "Gyroscope" by Sándor Kabai, Wolfram Demonstrations Project.
  2. ↑ Discover magazine 20 things you didn't know about tunnels (Number 8).
  3. ↑ Johann G. F. Bohnenberger (۱۸۱۷) "Beschreibung einer Maschine zur Erläuterung der Gesetze der Umdrehung der Erde um ihre Axe, und der Veränderung der Lage der letzteren" [Description of a machine for the explanation of the laws of rotation of the Earth around its axis, and of the change of the orientation of the latter] Tübinger Blätter für Naturwissenschaften und Arzneikunde, vol. ۳, pages ۷۲–۸۳. Available on-line at: http://www.ion.org/museum/files/File_1.pdf.
  4. ↑ The French mathematician Poisson mentions Bohnenberger's gyroscope as early as ۱۸۱۳: Simeon-Denis Poisson (۱۸۱۳) "Mémoire sur un cas particulier du mouvement de rotation des corps pesans" [Memoir on a special case of rotational movement of massive bodies], Journal de l'École Polytechnique, vol. ۹, pages ۲۴۷–۲۶۲. Available on-line at: http://www.ion.org/museum/files/File_2.pdf.
  5. ↑ A photograph of Bohnenberger's gyroscope is available on-line here: http://www.ion.org/museum/item_view.cfm?cid=5&scid=12&iid=24.
  6. ↑ Walter R. Johnson (January 1832) "Description of an apparatus called the rotascope for exhibiting several phenomena and illustrating certain laws of rotary motion", The American Journal of Science and Art, ۱st series, vol. ۲۱, no. ۲, pages ۲۶۵–۲۸۰. Available on-line at: http://books.google.com/books?id=BjwPAAAAYAAJ&pg=PA265&lpg=PR5&dq=Johnson+rotascope&ie=ISO-8859-1&output=html.
  7. ↑ Illustrations of Walter R. Johnson's gyroscope ("rotascope") appear in: Board of Regents, Tenth Annual Report of the Board of Regents of the Smithsonian Institution.... (Washington, D.C.: Cornelius Wendell, 1856), pages ۱۷۷–۱۷۸. Available on-line at: http://books.google.com/books?id=fEyT4sTd7ZkC&pg=PA178&dq=Johnson+rotascope&ie=ISO-8859-1&output=html.
  8. ↑ Wagner JF, "The Machine of Bohnenberger", The Institute of Navigation
  9. ↑ L. Foucault (۱۸۵۲) "Sur les phénomènes d’orientation des corps tournants entraînés par un axe fixe à la surface de la terre", Comptes rendus hebdomadaires des séances de l’Académie des Sciences (Paris), vol. ۳۵, pages ۴۲۴–۴۲۷. Available on-line (in French): http://www.bookmine.org/memoirs/pendule.html. Scroll down to "Sur les phénomènes d’orientation..."
  10. ↑ Circa 1852, Friedrich Fessel, a German mechanic and former secondary school teacher, independently developed a gyroscope. See: (۱) Julius Plücker (September 1853) "Über die Fessel'sche rotationsmachine", Annalen der Physik, vol. ۱۶۶, no. ۹, pages ۱۷۴–۱۷۷; (۲) Julius Plücker (October 1853) "Noch ein wort über die Fessel'sche rotationsmachine", Annalen der Physik, vol. ۱۶۶, no. ۱۰, pages ۳۴۸–۳۵۱; (۳) Charles Wheatstone (۱۸۶۴) "On Fessel's gyroscope", Proceedings of the Royal Society of London, vol. ۷, pages ۴۳–۴۸. Available on-line at: http://books.google.com/books?id=CtGEAAAAIAAJ&pg=RA1-PA307&lpg=RA1-PA307&dq=Fessel+gyroscope&source=bl&ots=ZP0mYYrp_d&sig=DGmUeU4MC8hAMuBtDSQn4GpAyWc&hl=en&ei=N4s9SqOaM5vKtgf62vUH&sa=X&oi=book_result&ct=result&resnum=9.
  11. ↑ MacKenzie, Donald. Inventing Accuracy: A Historical Sociology of Nuclear Missile Guidance. Cambridge: MIT Press, 1990. pp. ۳۱–۴۰. ISBN 0-262-13258-3
  12. ↑ MacKenzie, pp. ۴۰–۴۲.

12. One-Wheeled Robot-Gyrostat by Olga Kapustina and Yuri Martynenko Wolfram Demonstrations Project

برگرفته از «http://fa.wikipedia.org/w/index.php?title=ژیروسکوپ&oldid=9690064»