الکترون

الکترون

اوربیتال‌های اتم هیدروژن در سطوح مختلف انرژی. نواحی روشن‌تر، نواحی هستند که در هر لحظه از زمان، احتمال یافتن الکترون در آن نواحی بیشتر است.
آمار	فرمیون
نسل	اول
نیروهای بنیادی	جاذبه، الکترومغناطیس، نیروی ضعیف
نماد	−e یا −β
پادذره	پوزیترون (به آن پادالکترون هم گفته‌می‌شود)
نظریه‌پردازی	ریچارد لامینگ (۱۸۳۸–۱۸۵۱) جرج استونی (۱۸۷۴) و دیگران
کشف	جی جی تامسون (۱۸۹۷)
جرم	۶۹۶۹۹۱۰۹۳۸۲۹۱۰۰۰۰۰۰♠۹٫۱۰۹۳۸۲۹۱(۴۰)×۱۰−۳۱ kg ۶۹۹۶۵۴۸۵۷۹۹۰۹۴۶۰۰۰۰♠۵٫۴۸۵۷۹۹۰۹۴۶(۲۲)×۱۰−۴ u [۷۰۰۳۱۸۲۲۸۸۸۴۸۴۵۰۰۰۰♠۱۸۲۲٫۸۸۸۴۸۴۵(۱۴)]−1 u ۶۹۹۹۵۱۰۹۹۸۹۲۸۰۰۰۰۰۰♠۰٫۵۱۰۹۹۸۹۲۸(۱۱) MeV/c۲
بار الکتریکی	۳۰۱۸۸۳۹۷۸۲۳۵۱۳۰۰۰۰۰♠−۱ e ۳۰۱۸۸۳۹۷۸۲۳۴۳۵۰۰۰۰۰♠−۱٫۶۰۲۱۷۶۵۶۵(۳۵)×۱۰−۱۹ C ۳۰۰۹۵۱۹۶۷۹۵۴۹۰۰۰۰۰۰♠−۴٫۸۰۳۲۰۴۵۱(۱۰)×۱۰−۱۰ esu
اسپین	1⁄2

اِلِکترون (به انگلیسی: electron) (با نماد ⁻e یا ⁻β) یک ذره زیر اتمی‌‌ست با بار الکتریکی منفی و برابر با بار بنیادی. الکترون‌ها به نسل نخست از خانواده لپتون‌ها تعلق دارند و به‌طور عمومی به عنوان ذره بنیادی شناخته می‌شوند زیرا هیچ جزء و زیرساختار تشکیل‌دهنده شناخته‌شده‌ای ندارند. الکترون جرمی تقریباً برابر با یک بر روی ۱۸۳۶ جرم پروتون دارد. ویژگی‌های کوانتومی الکترون شامل تکانه زاویه‌ای ذاتی (اسپین) با مقدار نیمه‌صحیح بر حسب ħ (ثابت کاهیدهٔ پلانک)است و این یعنی الکترون یک نوع فرمیون است. به دلیل فرمیون بودن، طبق اصل طرد پاولی، دو الکترون مختلف نمی‌توانند حالات کوانتومی یکسانی را اشغال کنند. الکترون‌ها، همانند همهٔ مواد، هم ویژگی‌های ذره‌ای و هم موجی را دارا هستند، یعنی هم می‌توانند با ذرات دیگر برخورد کنند و هم مانند نور دچار پراش شوند. مشاهده ویژگی‌های موجی الکترون نسبت به ذراتی مانند نوترون و پروتون آسان‌تر است زیرا جرم الکترون کمتر است و در نتیجه طول موج دوبروی آن برای انرژی‌های معمول بالاتر است.

در بسیاری از پدیده‌های فیزیکی مانند الکتریسیته، مغناطیس و رسانش گرمایی، الکترون‌ها نقشی اساسی را ایفا می‌کنند و همچنین در برهم‌کنش‌های گرانشی، الکترومغناطیسی و هسته‌ای ضعیف نیز شرکت می‌کند. الکترون یک میدان الکتریکی در اطراف خود ایجاد می‌کند. یک الکترون در حال حرکت نسبت به یک ناظر، یک میدان مغناطیسی تولید می‌کند، و میدان‌های مغناطیسی خارجی نیز باعث انحراف مسیر حرکت الکترون می‌شوند. هنگامی که یک الکترون شتاب می‌گیرد، انرژی را به شکل فوتون جذب یا تابش می‌کند. وسایل آزمایشگاهی با بهره‌گیری از میدان‌های الکترومغناطیسی توانایی دربرگرفتن و مشاهده الکترون‌های تکی و پلاسمای الکترون را دارند و تلسکوپ‌های ویژه‌ای نیز وجود دارند که می‌توانند پلاسماهای الکترون را در فضا آشکار سازند. الکترون کاربرهای فراوانی دارد که از جمله آن‌ها می‌توان به الکترونیک، جوشکاری با تشعشعات الکترونی، لامپ پرتوی کاتدی، میکروسکوپ الکترونی، پرتودرمانی، لیزر الکترون آزاد، آشکارسازهای یونیزاسیون گازی و شتاب‌دهنده ذره‌ای اشاره نمود.

برهم‌کنش‌های دربرگیرنده الکترون و ذرات زیراتمی دیگر در دانش‌هایی مانند شیمی و فیزیک هسته‌ای مورد توجه ویژه‌ای قرار می‌گیرند. برهم‌کنش نیروی کولنی میان پروتونهای مثبت هسته اتم و الکترون‌های منفی باعث تشکیل شدن اتم می‌شود. یونیزه‌شدن و تغییر در نسبت‌های ذرات باعث تغییر در انرژی بستگی سیستم می‌شود. تبادل یا به اشتراک‌گذاری الکترون میان دو یا چند اتم عامل اصلی بوجودآمدن پیوندهای شیمیایی است. فیلسوف طبیعی بریتانیایی، ریچارد لامینگ نخستین بار در سال ۱۸۳۸ فرضیه‌ای شامل مفهوم یک مقدار تجزیه‌ناپذیر بار الکتریکی برای توضیح ویژگی‌های شیمیایی اتم‌ها ارائه داد. فیزیکدان ایرلندی، جرج استونی، در سال ۱۸۹۱ نام این بار را الکترون گذاشت و جی جی تامسون و تیم متشکل از فیزیکدانان بریتانیایی او این ذره را در سال ۱۸۹۷ شناسایی کردند. الکترون‌ها در واکنش‌های هسته‌ای مانند هسته‌زایی در ستارگان نیز می‌توانند شرکت کنند که در آنجا با نام ذرات بتا شناخته می‌شوند. الکترون‌ها ممکن است در واپاشی بتای ایزوتوپ‌های رادیواکتیو و همچنین در برخوردهای پرانرژی، مانند وقتی که پرتو کیهانی وارد اتمسفر می‌شود، به‌وجود آیند. پادذره الکترون، پوزیترون نام دارد که دقیقاً مانند الکترون است اما بار الکتریکی و دیگر بارهای آن علامت مخالف با الکترون دارند. وقتی یک الکترون به یک پوزیترون برخورد می‌کند، ممکن است هردو کاملاً نابود شوند و فوتونهای پرتو گاما تولید کنند.

تاریخچه

همچنین ببینید: پیشینه الکتریسیته

یونانیان باستان متوجه شدند که وقتی کهربا با پشم مالش داده شود، اشیای کوچک را به سمت خود جذب می‌کند. این پدیده به همراه آذرخش نخستین تجربه‌های ثبت‌شده بشر از الکتریسیته هستند. در دههٔ ۱۶۰۰ دانشمندی انگلیسی به نام ویلیام گیلبرت در مقاله‌ای با عنوان «مگنت (De Magnete)»، برای اشاره به این ویژگی جذب اشیای کوچک پس از مالش، واژهٔ لاتین جدیدی به نام الکتریکوس را به کار برد. واژه‌های الکتریسیته و الکتریک هر دو از واژهٔ لاتین الکتروم (هم چنین ریشهٔ ترکیب همان اسم)، که خود برگرفته از واژهٔ یونانی ήλεκτρον (الکترون) به معنی کهربا است، مشتق شده‌اند.

در اوایل دهه ۱۷۰۰، فرانسیس هاوکسبی و یک شیمی‌دان فرانسوی به نام شارل فرانسوا دو فی به‌طور جداگانه چیزی کشف کردند که از آن با عنوان دو گونه متفاوت از الکتریسیته مالشی یاد کردند؛ یکی تولید شده از مالش شیشه، و دیگری از مالش رزین. دوفی نتیجه گرفت که الکتریسیته از دو شار الکتریکی با نام‌های «ویترئوس» و «رزینوس» تشکیل شده‌است که مالش باعث جدا شدن آن‌ها از یکدیگر می‌شود و هنگامی که با هم ترکیب شوند، یکدیگر را خنثی می‌کنند. یک دهه بعد، بنجامین فرانکلین پیشنهاد داد که الکتریسیته از انواع متفاوتی از شاره‌های الکتریکی ناشی نمی‌شود، بلکه ناشی از یک نوع شاره الکتریکی تحت فشارهای مختلف است. او همانند نام‌گذاری امروزی بارهای الکتریکی، آن‌ها را به ترتیب مثبت و منفی نامید. فرانکلین حامل بار را مثبت در نظر گرفته بود، اما به درستی تشخیص نداده بود که کدام شرایط مربوط به افزونی بار و کدام مربوط به کمبود بار بود.

در ۱۸۰۷- ۱۸۰۸ همفری دیوی شیمی دان انگلیسی با تجزیه مواد مرکب به کمک جریان الکتریسیته، ۵ عنصر پتاسیم، سدیم، کلسیم، استرنسیم و باریم را کشف کرد و نتیجه گرفت که عناصر با نیروی جاذبه ای به هم متصل هستند که ماهیت الکتریکی دارد.

در ۱۸۳۲-۱۸۳۳ مایکل فارادی هم همانند دیوی آزمایش‌هایی را به وسیله برقکافت انجام داد و رابطه بین مقدار الکتریسیته مصرف شده و میزان ماده مرکب تجزیه شده به دست آورد.

بین سال‌های ۱۸۳۸ تا ۱۸۵۱، فیلسوف طبیعی انگلیسی ریچارد لامینگ این ایده را مطرح نمود که اتم متشکل از یک هستهٔ مادی است که توسط ذرات زیر اتمی با بار الکتریکی واحد در بر گرفته شده‌است. در اوایل سال ۱۸۳۶، یک فیزیکدان آلمانی به نام ویلهلم ادوارد وبر، نظریه‌ای مطرح کرد که طبق آن، الکتریسیته متشکل از شاره‌های باردار مثبت و منفی است که برهم‌کنش میان آن‌ها از قانون مربع معکوس پیروی می‌کند. در سال ۱۸۷۴، فیزیکدان ایرلندی جورج جانستون استونی، پس از مطالعه پدیده برق‌کافت، پیشنهاد کرد که یک مقدار واحد مشخص از الکتریسیته وجود دارد که همان بار یون تک ظرفیتی است. او توانسته‌بود، مقدار این بار بنیادی را به وسیلهٔ قوانین برق‌کافت فاراده تخمین بزند. هرچندکه او معتقد بود این بارها به‌طور دائمی به اتم‌ها متصل هستند و نمی‌توان آن‌ها را از اتم جدا کرد. در سال ۱۸۸۱ یک فیزیکدان آلمانی به نام هرمان وان هلمولتز ادعا نمود که بارهای مثبت و منفی هر دو به قسمت‌های بنیادی تری تقسیم می‌شوند که هر کدام از آن‌ها «مانند اتم‌های الکتریسیته رفتار می‌کنند».

استونی در ابتدا واژه الکترولیون را در سال ۱۸۸۱ ابداع نمود. ده سال بعد آن را به الکترون تغییر داد تا با آن، این بارهای بنیادی را توصیف کند. او در سال ۱۸۹۴ چنین می‌نویسد: «... تخمینی از این قابل توجه‌ترین مقدار واحد پایه‌ای از الکتریسیته زده شد، که از آن زمان تصمیم گرفتم که برای آن نام الکترون را پیشنهاد بدهم». در سال ۱۹۰۶ پیشنهادی برای تغییر آن به الکتریون مطرح شد که با شکست روبه‌رو شد زیرا هندریک لورنتز ترجیح داد نام الکترون را نگه دارد. واژه الکترون ترکیبی از واژه الکتریک و پسوند یون می‌باشد، پسوند -ون که در نامیدن ذرات زیراتمی دیگر مانند پروتون و نوترون نیز به‌کار می‌رود از الکترون گرفته شده‌است.

کشف

یک پرتو از الکترون‌ها که به شکل دایره و به وسیلهٔ یک میدان مغناطیسی منحرف شده‌است.

یوهان ویلهلم هیترف، فیزیکدان آلمانی، رسانایی الکتریکی را در گازهای رقیق مطالعه نمود: در سال ۱۸۶۹ او تابشی را کشف کرد که از کاتد منتشر می‌شد و اندازهٔ آن با کاهش فشار گاز افزایش می‌یافت. در سال ۱۸۷۶، یک دانشمند آلمانی به نام اویگن گلدشتاین، نشان داد که پرتوهای این تابش سایه ایجاد می‌کنند و این پرتوها را پرتوهای کاتدی نامید. در طول دههٔ ۱۸۷۰، یک شیمیدان و فیزیکدان انگلیسی به نام سر ویلیام کروکس، نخستین لامپ پرتو کاتدی از نوع محفظه خلأ را ساخت. او سپس نشان داد که پرتوهای تابناکی که در داخل لوله پدیدار می‌شوند، حامل انرژی هستند و از کاتد به سوی آند حرکت می‌کنند. علاوه بر این، او توانست با بهره‌گیری از یک میدان مغناطیسی مسیر پرتوها را منحرف کند و بدین ترتیب نشان داد که این پرتوها به‌گونه‌ای رفتار می‌کنند که گویی بار منفی دارند. در سال ۱۸۷۹ او پیشنهاد داد که این ویژگی‌ها را می‌توان با آنچه که وی «مادهٔ پرتوزا» نامیده‌بود، توضیح داد. پیشنهاد وی این بود که این حالت چهارمی از ماده است که شامل مولکولهایی با بار منفی می‌شود که با سرعت بالا از کاتد تابیده می‌شوند.

یک فیزیکدان آلمانی‌الاصل انگلیسی به نام آرتور شوستر، آزمایش‌ها کروکس را گسترش داد و چند صفحه فلزی را هم‌راستا با پرتوهای کاتدی درون محفظه خلاء قرار داد و بین صفحات، پتانسیل الکتریکی ایجاد نمود. میدان ایجادشده پرتوها را به سوی صفحهٔ با بار مثبت منحرف می‌کرد، که گواه دیگری بر منفی بودن بار الکتریکی این پرتوها بود. در سال ۱۸۹۰، شوستر، با اندازه‌گیری این انحراف به ازای یک جریان معین، توانست نسبت جرم به بار اجزای تشکیل‌دهنده این پرتو را تخمین بزند. از آنجا که این نسبت بیش از هزار بار بزرگتر از آنچه انتظار می‌رفت بود، عدهٔ کمی به آن توجه کردند.

در سال ۱۸۹۲، هندریک لورنتز پیشنهاد داد که جرم این ذرات (الکترون‌ها) ممکن است ناشی از بار الکتریکی آن‌ها باشد.

در سال ۱۸۹۶ یک فیزیکدان انگلیسی به نام ج. ج تامسون با همکارانش به نام‌های جان سیلی تاونزند و هارولد ویلسون، آزمایش‌هایی را انجام دادند که نشان داد پرتوهای کاتدی، برخلاف آنچه پیش‌تر پنداشته می‌شد، موج، اتم یا مولکول نیستند، بلکه از ذرات منحصربه‌فردی تشکیل شده‌اند. از آنجاییکه انحراف این ذرات با اندازه بار ذره متناسب بوده و با جرم آن نسبت عکس دارد، تامسون توانست تخمین‌های خوبی از بار e و جرم m زد که نشان می‌داد، ذرات پرتو کاتدی، که او آن‌ها را «کورپاسکل» می‌نامیده‌بود، احتمالاً دارای جرمی برابر با حدود یک‌هزارم جرم سبک‌ترین یون شناخته‌شده یعنی هیدروژن هستند. او همچنین نشان داد که نسبت بار به جرم آن‌ها یعنی e/m به جنس کاتد بستگی ندارد. افزون بر این، او نشان داد که ذرات با بار منفی تولید شده به وسیلهٔ مواد رادیواکتیو، مواد حرارت داده‌شده و مواد تحت تابش نورانی، یکسان هستند. سپس شعاع انحرافی را که بر اثر شدت میدان مغناطیسی معینی ایجاد شده بود، اندازه گرفت و سپس میدان الکتریکی لازم برای برقراری توازن با میدان مغناطیسی به شکلی که انحراف مؤثری در پرتو کاتدی مشاهده نشود را تعیین نمود. از این راه او نسبت بار به جرم ذره را q/m= ۱.۷۵۸۸۲۰۰۲۴×۱۰^۸ C/g اندازه‌گیری کرد.

نام الکترون دوباره برای این ذرات توسط یک فیزیکدان ایرلندی به نام جرج فیتزجرالد پیشنهاد داده شد و از آن زمان تاکنون این نام مورد پذیرش جهانی قرار گرفته‌است.

رابرت میلیکان

در سال ۱۸۹۶ یک فیزیکدان فرانسوی به نام هانری بکرل، هنگام مطالعهٔ مواد معدنی دارای ویژگی فلوئورسانس، کشف کرد که این مواد بدون نیاز به قرار گرفتن در معرض یک منبع انرژی خارجی، پرتو تابش می‌کنند. این مواد پرتوزا مورد علاقه فراوان دانشمندان از جمله فیزیکدان نیوزلندی به نام ارنست رادرفورد قرارگرفت. او کشف کرد که این مواد، ذره تابش می‌کنند. او این ذرات را بر اساس توانایی نفوذشان در مواد، آلفا و بتا نامید. در سال ۱۹۰۰ بکرل نشان داد که پرتوهای بتای تولید شده به وسیلهٔ رادیوم توسط میدان الکتریکی منحرف می‌شوند و نسبت جرم به بار آن‌ها با پرتوهای کاتدی یکسان است. این مشاهده، دیدگاه وجود الکترون‌ها به عنوان جزئی از اتم‌ها را تقویت کرد.

اندازه گیری بار الکترون

نوشتار اصلی: آزمایش قطره روغن

در سال ۱۹۰۹ بار الکترون با دقت بیشتری توسط دانشمندان آمریکایی به نام‌های رابرت میلیکان و هاروی فلچر به‌وسیله آزمایش قطره روغن آن‌ها اندازه‌گیری شد که نتایج آن در سال ۱۹۱۱ منتشر نمود. در این آزمایش از اثر پرتوهای ایکس برای تولید الکترون از مولکول‌های هوا استفاده شده بود. سپس قطره‌های ریز روغن به هوا پاشیده می‌شد تا الکترون‌ها را جذب کند و از یک میدان الکتریکی استفاده شده بود تا از سقوط قطره‌های کوچک روغن بر اثر گرانش جلوگیری کنند. در واقع بار الکتریکی بین دو صفحه مدار می‌توانست به شکلی تنظیم شود که قطره‌های روغن سقوط نکنند. این وسیله می‌توانست بار الکتریکی را برای تعداد کمی همچون ۱–۱۵۰ یون را با خطای کمتر از۰٫۳٪ اندازه بگیرد. پیش از این آزمایش‌های مشابهی توسط گروه تامسون انجام شده بود، که در آن‌ها از بخار قطرات ریز آب باردار که به وسیله برقکافت تولید شده بودند، استفاده شده بود، و در سال ۱۹۱۱ نیز آبرام ایوف به‌طور جداگانه به همان نتیجهٔ میلیکان با استفاده از ریزذرات فلزات دست یافت، و نتایج آن را در سال ۱۹۱۳ منتشر کرد. هر چند که قطره‌های روغن به دلیل سرعت تبخیر کمتر، از قطره‌های آب پایدار تر و در نتیجه برای آزمایش دقیق در زمان‌های طولانی مناسب تر بودند. از سوی دیگر ممکن بود که یک قطره روغن بیش از یک الکترون جذب کند و در نتیجه مقدار بارهای محاسبه شده بر روی همه قطره‌های روغن همسان نباشند اما همه آن‌ها مضربی ساده از یک مقدار معین بودند. بنابراین یک الکترون باری برابر با q=−۱.۶۰۲۱۷۶۴۸۷(40)×۱۰^−۱۹ C دارد. با توجه به میزان q/m تعیین شده توسط تامسون و بار الکتریکی یک الکترون می‌توان جرم الکترون را اینگونه محاسبه نمود: m=q/m= ۹/۱۰۹۶x۱۰^{−۲۸ g}

در اوایل قرن بیستم مشخص شد که در شرایط خاصی، یک ذرهٔ باردار متحرک با سرعت بالا در طول مسیر خود، باعث میعان بخار آب فوق اشباع می‌شوند. در سال ۱۹۱۱ چارلز ویلسون از این ویژگی برای طراحی اتاقک ابر خود استفاده کرد که امکان عکس گرفتن از مسیر ذرات باردار، مانند الکترون‌های پرسرعت را فراهم نمود.

نظریهٔ اتمی

نوشتار اصلی: نظریه اتمی

مدل اتمی بور، نشان دهندهٔ حالت‌های الکترون با انرژی کوانتیده به وسیلهٔ شمارهٔ n. هنگامی که الکترون به یک مدار پایین‌تر می‌افتد یک فوتون تابش تابش می‌کند که با اختلاف انرژی بین مدارها یکسان است.

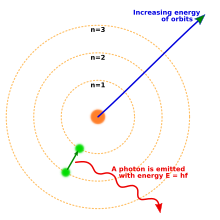
در سال ۱۹۱۴ آزمایش‌های انجام شده به وسیلهٔ فیزیکدانانی چون ارنست رادرفورد، هنری موزلی، جیمز فرانک و گوستاو هرتز، تا حد زیادی تصویر ساختار اتم را به صورت یک هسته فشرده با بار مثبت و احاطه‌شده توسط الکترون‌هایی با جرم کمتر، تثبیت نموده‌بودند. در سال ۱۹۱۳ یک فیزیکدان دانمارکی به نام نیلز بور چنین فرض نمود که الکترون در حالت‌های (مدارهای) انرژی کوانتایی مشخصی قرار می‌گیرد که انرژی آن‌ها توسط تکانه زاویه‌ای مدارهای الکترون در اطراف هسته تعیین می‌شود. الکترون‌ها می‌توانند با نشر یا جذب فوتون‌هایی با بسامدهای مشخص، بین این حالت‌ها یا مدارها حرکت کنند. او به وسیلهٔ این مدارهای کوانتایی، توضیح دقیقی در مورد خطوط طیفی اتم هیدروژن ارائه داد. با این وجود، مدل بور از توضیح دلیل شدت نسبی خطوط طیف و همچنین توضیح طیف اتم‌های پیچیده‌تر ناتوان بود.

پیوندهای شیمیایی بین اتم‌ها توسط گیلبرت نیوتون لوییس توضیح داده شدند. او در سال ۱۹۱۶ پیشنهاد داد که یک پیوند کووالانسی بین دو اتم به وسیلهٔ دو الکترون به وجود می‌آید که بین دو اتم به اشتراک گذاشته می‌شوند. بعدها در سال ۱۹۲۷ والتر هایتلر و فریتس لندن توضیح کاملی در مورد شکل‌گیری جفت‌الکترون و پیوند شیمیایی به زبان مکانیک کوانتومی ارائه دادند. در سال ۱۹۱۹ یک شیمیدان آمریکایی به نام ایروینگ لانگمویر مدل اتمی استاتیک لوییس را گسترش داد و معتقد بود که همهٔ الکترون‌ها در پوسته‌های کروی (تقریباً) هم‌مرکز با ضخامت یکسان به‌طور متوالی توزیع شده‌اند. پوسته‌ها نیز به نوبه خود به سلول‌هایی تقسیم می‌شدند که هر کدام از آن‌ها شامل یک جفت الکترون بود. با استفاده از این مدل لانگمویر قادر بود تا به‌طور کیفی، ویژگی‌های شیمیایی همهٔ عناصر جدول تناوبی را توضیح دهد، که بنا بر قانون تناوبی تصور می‌شد تا حدود زیادی خودشان را تکرار می‌کنند.

در سال ۱۹۲۴ یک فیزیکدان اتریشی به نام ولفگانگ پاولی دریافت که ساختار پوسته‌مانند اتم را می‌توان به وسیله مجموعه‌ای از ۴ پارامتر توضیح داد که تمام حالت‌های کوانتومی انرژی را تعریف می‌کنند، به شرط این که هر یک از این حالت‌ها به وسیلهٔ تنها یک الکترون اشغال شود. (این محدودیت که یک حالت کوانتومی انرژی نمی‌تواند توسط بیش از یک الکترون اشغال شود، به نام اصل طرد پاولی شهرت یافت) سازوکار فیزیکی برای توضیح پارامتر چهارم این مجموعه پارامترهای چهارگانه، که دو مقدار متمایز ممکن برای آن وجود دارد، به وسیلهٔ فیزیکدان‌های هلندی به نام‌های ساموئل گودسمیت و جرج اولنبک، ارائه شد. در سال ۱۹۲۵ آن‌ها پیشنهاد کردند که الکترون علاوه بر اندازه حرکت زاویه‌ای ناشی از حرکت دایره‌ای، خودش نیز دارای یک اندازه حرکت زاویه‌ای و گشتاور مغناطیسی ذاتی است. تکانه زاویه‌ای ذاتی الکترون با نام اسپین شهرت یافت، و شکاف‌های ابهام‌آمیز موجود در خطوط طیفی مشاهده‌شده توسط یک طیفسنج با وضوح بالا را توضیح داد؛ امروزه این پدیده به عنوان شکاف ساختار ریز شناخته می‌شود.

مکانیک کوانتومی

همچنین ببینید: تاریخ مکانیک کوانتومی

در مکانیک کوانتومی رفتار یک الکترون در یک اتم به وسیلهٔ یک اوربیتال توصیف می‌شود که به جای مدار، در واقع یک توزیع احتمال است. در تصویر بالا سایه نشان دهندهٔ احتمال نسبی یافتن الکترون است، که انرژی آن متناظر با اعداد کوانتومی در آن نقطه است.

در سال ۱۹۲۴ یک فیزیکدان فرانسوی به نام لوییس دوبروی در مقاله اش با عنوان (تحقیق دربارهٔ نظریهٔ کوانتوم) فرضیه‌ای را مطرح کرد که همهٔ مواد، مانند نور، دارای یک موج دوبروی می‌باشند. یعنی در شرایط مناسب، الکترون‌ها یا مواد دیگر ممکن است از خودشان ویژگی‌های ذرات یا امواج را بروز دهند. ویژگی‌های ذره‌ای یک ذره هنگامی بروز می‌کنند که این‌گونه نشان می‌دهد که در هر لحظه از زمان، در طول مسیرش یک موقعیت محلی در فضا دارد. ماهیت موجی هنگامی مشاهده می‌شود که مثلاً یک پرتو نور از درون شکاف‌های موازی عبور می‌کند و الگوهای تداخلی ایجاد می‌کند. در سال ۱۹۲۷، الگوهای تداخلی برای یک پرتو از الکترون‌ها و با استفاده از یک پرده نازک فلزی، توسط یک فیزیکدان انگلیسی به نام جورج پاجت تامسون مشاهده شد و همچنین دو فیزیکدان آمریکایی به نام‌های کلینتون دیویسون و لستر گرمر این اثر را با استفاده از یک بلور نیکل مشاهده کردند.

پیش‌بینی دوبروی در مورد ماهیت موجی الکترون سبب شد شرودینگر معادله موجی برای الکترون‌های در حال حرکت تحت تأثیر هسته در اتم، ارائه دهد. در سال ۱۹۲۶، این معادله، یعنی معادله شرودینگر به شکل موفقیت‌آمیزی چگونگی انتشار امواج الکترونی را توصیف کرد. این معادله موج به جای اینکه به پاسخی برای تعیین مکان الکترون در طول زمان بینجامد، می‌تواند برای پیش‌بینی احتمال یافتن یک الکترون در نزدیکی یک مکان مورد استفاده قرار گیرد، به ویژه در نواحی از فضا که الکترون در آن مقید است، زیرا معادله موج الکترون در این نواحی با گذشت زمان تغییر نمی‌کند. این دیدگاه منجر به فرمول‌بندی دوم مکانیک کوانتومی (که فرمول‌بندی نخست آن توسط هایزنبرگ در سال ۱۹۲۵ انجام شده‌بود) شد و پاسخ‌های معادله شرودینگر مانند هایزنبرگ منجر به نتیجه‌گیری‌هایی در مورد حالات انرژی یک الکترون در اتم هیدروژن می‌شد که معادل همان‌هایی بودند که توسط بور در سال ۱۹۱۳ نتیجه‌گیری شده‌بود و به عنوان عامل ایجاد خطوط طیفی هیدروژن شناخته می‌شدند. هنگامی که اسپین و برهم‌کنش میان الکترون‌ها در نظر گرفته شدند، مکانیک کوانتومی بعدها این امکان را فراهم نمود که قرارگیری الکترون‌ها در اتم‌های با اعداد اتمی بالاتر از هیدروژن نیز، پیش‌بینی شوند.

در سال ۱۹۲۸ پائول دیراک بر مبنای کار ولفگانگ پاولی، مدلی از الکترون به نام معادلهٔ دیراک ارائه داد که با نظریه نسبیت سازگار بود و با بکار بردن آثار نسبیتی و تقارن در فرمول‌بندی هامیلتونی مکانیک کوانتومی میدان الکترومغناطیسی. در سال ۱۹۳۰ دیراک به منظور رفع برخی اشکالات موجود در معادلهٔ نسبیتی اش، یک مدل از خلأ به عنوان یک دریای نامتناهی از ذرات با انرژی منفی ارائه داد که دریای دیراک نامیده شد. این موضوع منجر شد که او وجود پوزیترون را که پادماده همتای الکترون است، پیش‌بینی کند. این ذره در سال ۱۹۳۲ توسط کارل اندرسون کشف شد و پیشنهاد داد که الکترون‌های استاندارد نگاترون نامیده شوند و الکترون به عنوان یک عبارت عمومی بکار برده شود که هر دو گونه دارای بار مثبت و منفی را توصیف می‌کند. ش در سال ۱۹۴۷، ویلیس اوژن لمب به هنگام همکاری با یک دانشجوی فوق‌لیسانس به نام رابرت رادرفورد، متوجه شد که حالت‌های کوانتومی معینی از اتم هیدروژن که باید انرژی‌های یکسانی داشته باشند نسبت به یکدیگر تغییر می‌کنند که این تفاوت موجود با نام تغییر لمب شناخته می‌شود. تقریباً در همان زمان، پولیکارپ کوش هنگام کار با هنری فولی، کشف کرد که گشتاور مغناطیسی الکترون کمی بیشتر از آن چیزی است که توسط نظریه دیراک پیش‌بینی شده‌است. این تفاوت کوچک بعدها گشتاور دوقطبی مغناطیسی نابهنجار الکترون نامیده شد. این اختلاف بعدها توسط نظریه الکترودینامیک کوانتومی که اواخر دههٔ ۱۹۴۰ توسط سین ایتیرو توموناگا، جولیان شوینگر و ریچارد فاینمن ارائه شده بود، توضیح داده‌شد.

شتاب دهنده‌های ذرات

با پیدایش دستگاه‌های شتاب دهندهٔ ذره‌ای در خلال نیمهٔ اول قرن بیستم، فیزیکدانان کاوش‌های ژرفتری در مورد ویژگی‌های ذرات زیر اتمی آغاز نمودند. نخستین تلاش موفقیت‌آمیز برای شتاب بخشیدن به الکترون‌ها با استفاده از القای الکترومغناطیسی را دونالد کرست در سال ۱۹۴۲ انجام داد. بتاترون اولیه وی به انرژی‌هایی در سطح ۲٫۳MeV رسید، درحالی‌که بتاترون‌های بعدی به انرژیهایی در حد ۳۰۰MeV دست یافتند. در سال ۱۹۴۷ تابش سینکروترون با استفاده از یک سینکروترون الکترونی ۷۰MeV و در شرکت جنرال الکتریک کشف شد. این تابش از شتاب گرفتن الکترون‌ها و حرکت آن‌ها با سرعتی نزدیک به سرعت نور در درون یک میدان مغناطیسی، ناشی می‌شود.

اولین برخورد دهنده ی ذرات با انرژی بالا آدون نام داشت که انرژی پرتو آن ۱٫۵GeV بود و در سال ۱۹۶۸ شروع به کار کرد. این وسیله هم به الکترون‌ها و هم به پوزیترون‌ها در جهت مخالف مم شتاب می‌داد، که به شکل مؤثری، انرژی برخورد آن‌ها را در مقایسه با برخورد الکترون با یک هدف ساکن، دوبرابر می‌کرد. برخورددهنده بزرگ الکترون-پوزیترون (LEP) در سرن که از سال ۱۹۸۹ تا ۲۰۰۰ در حال کار بود، توانست به انرژی‌های برخوردی در حد ۲۰۹GeV دست یابد و سنگ محک مهمی برای مدل استاندارد فیزیک ذرات بود.

حبس‌نمودن یک تک الکترون

الکترون‌های تکی را امروزه می‌توان در یک ترانزیستور فوق کوچک (۲۰x۲۰ نانومتر) سی‌موس محبوس نمود که در دماهای پایینی از ۲۶۹- تا ۲۵۸- درجه سانتیگراد عمل می‌کند. تابع موج الکترون در یک شبکه نیمه‌هادی پخش می‌شود و با الکترون‌های ظرفیت برهمکنشی قابل چشم‌پوشی دارد و می‌توان با جایگزینی جرم آن با تانسور جرم مؤثر، از صوری‌سازی تک‌ذره استفاده نمود

ویژگی‌ها

طبقه‌بندی

مدل استاندارد ذرات بنیادی. الکترون در گوشهٔ پایین و سمت چپ قرار دارد.

در مدل استاندارد فیزیک ذرات، الکترون‌ها به گروهی از ذرات زیر اتمی به نام لپتونها تعلق دارند که ذرات بنیادی یا اولیه در نظر گرفته می‌شوند. الکترون‌ها دارای کمترین مقدار جرم در میان لپتون‌های باردار (و یا هر نوع ذره دارای بار الکتریکی) هستند و متعلق به اولین نسل ذرات بنیادی هستند. دومین و سومین نسل لپتون‌های باردار میون و تاو هستند که از نظر بار، اسپین و برهم کنش با الکترون‌ها یکسان بوده ولی دارای جرم بیشتری می‌باشند. لپتون‌ها از نظر نداشتن برهم کنش قوی با جزء دیگر تشکیل دهندهٔ ماده به نام کوارک تفاوت دارند. همهٔ اعضای گروه لپتون‌ها فرمیون هستند زیرا همگی آن‌ها دارای اسپین نیمه‌صحیح هستند؛ الکترون دارای اسپین ^۱⁄_۲ است.

ویژگی‌های بنیادی

جرم نامتغیر یک الکترون تقریباً ۶۹۶۹۹۱۰۹۰۰۰۰۰۰۰۰۰۰۰♠۹٫۱۰۹×۱۰^−۳۱ کیلوگرم یا ۶۹۹۶۵۴۸۹۰۰۰۰۰۰۰۰۰۰۰♠۵٫۴۸۹×۱۰^−۴ واحد جرم اتمی است. برپایه اصل هم‌ارزی جرم-انرژی اینشتین، این میزان جرم معادل با انرژی سکونی برابر ۰٫۵۱۱ مگاالکترون‌ولت است. نسبت جرم پروتون به الکترون در حدود ۱۸۳۶ است. مشاهدات اخترشناسی نشان داده‌است که همان‌طور که مدل استاندارد پیش‌بینی می‌کند، نسبت جرم پروتون به الکترون حداقل در نیمی از عمر جهان، همین مقدار را داشته‌است.

الکترون دارای بار الکتریکی برابر با ۳۰۱۸۸۳۹۸۰۰۰۰۰۰۰۰۰۰۰♠−۱٫۶۰۲×۱۰^−۱۹ کولن است که به عنوان یکای استاندارد بار الکتریکی برای ذرات زیراتمی در نظر گرفته‌می‌شود و با نام بار بنیادی نیز شناخته‌می‌شود. این بار بنیادی عدم قطعیت استانداردی به اندازه ۶۹۹۲۲۲۰۰۰۰۰۰۰۰۰۰۰۰۰♠۲٫۲×۱۰^−۸ دارد. در محدوده دقت آزمایش‌های تجربی، میزان بار الکترون برابر با بار پروتون و با علامت مخالف آن است. از آنجاییکه نماد e برای بار بنیادی به‌کاربرده می‌شود، معمولاً الکترون را با نماد ^-e نمایش می‌دهند که علامت منفی نشان‌دهنده منفی بودن بار آن است. پوزیترون را با نماد ⁺e نمایش می‌دهند زیرا ویژگی‌هایش مانند الکترون است با این تفاوت که بار آن مثبت است.

الکترون دارای یک تکانه زاویه‌ای ذاتی یا اسپین به اندازه ^۱⁄_۲ است. به دلیل این ویژگی الکترون یک ذره اسپین-^۱⁄_۲ به‌شمار می‌آید. اندازه اسپین چنین ذراتی برابر با

^√۳⁄_۲ ħ

است و اندازه تصویر اسپین روی هر محور ^ħ⁄_۲± است. افزون بر اسپین، الکترون یک گشتاور مغناطیسی ذاتی نیز در امتداد محور اسپین خود دارد. مقدار آن تقریباً برابر با یک مگنتون بور است که ثابتی فیزیکی با اندازه ۶۹۷۶۹۲۷۴۰۰۹۱۴۹۹۹۹۹۹♠۹٫۲۷۴۰۰۹۱۵(۲۳)×۱۰^−۲۴ ژول بر تسلا می‌باشد.

جهت‌گیری اسپین نسبت به گشتاور الکترون یکی از ویژگی‌های ذرات بنیادی به نام مارپیچگی را تعریف می‌کند.

الکترون هیج زیرساختار شناخته‌شده‌ای ندارد و گمان می‌رود که یک ذره نقطه‌ای با بار نقطه‌ای و بدون اندازه فضایی باشد. در فیزیک کلاسیک، تکانه زاویه‌ای و گشتاور مغناطیسی یک جسم به ابعاد فیزیکی‌اش بستگی دارند. از این رو مفهوم یک الکترون بدون بعد که دارای این ویژگی‌ها باشد، با مشاهدات تجربی در آزمایش‌های دام پنینگ، که به شعاع متناهی غیر صفر الکترون اشاره می‌کنند، در تناقض به نظر می‌رسد. یک توضیح ممکن برای این شرایط متناقض‌نما در مبحث ذرات مجازی و با در نظرگرفتن تبدیل فولدی-ووتویسن مطرح می‌شود. مسئله شعاع الکترون یکی از مسائل چالش‌آمیز در فیزیک نظری نوین است. پذیرفتن فرضیه متناهی بودن شعاع الکترون با پیش‌فرض‌های نظریه نسبیت عام در تناقض است. از سوی دیگر، یک الکترون نقطه‌ای (شعاع صفر) نیز مشکلات ریاضیاتی جدی ایجاد می‌کند زیرا خود-انرژی الکترون به بی‌نهایت میل می‌کند. این جنبه‌ها به‌طور مفصل توسط دیمیتری ایواننکو و آرسنی سوکولوف تحلیل شده‌است.

مشاهدات مربوط به یک تک الکترون در یک دام پنینگ نشان می‌دهد که حداکثر شعاع ممکن برای ذره ۶۹۷۹۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰♠۱۰×۱۰^−۲۲ m متر است. یک ثابت فیزیکی به نام شعاع کلاسیک الکترون وجود دارد که مقدار بسیار بیشتری برابر با ۶۹۸۵۲۸۱۷۸۹۹۹۹۹۹۹۹۹۹♠۲٫۸۱۷۹×۱۰^−۱۵ m متر دارد که از شعاع پروتون نیز بزرگتر است. واژه کلاسیک در اینجا اشاره به محاسبه ساده‌انگارانه‌ای می‌کند که آثار مکانیک کوانتومی را نادیده می‌گیرد؛ در واقعیت، شعاع کلاسیک الکترون ارتباط اندکی با ساختار بنیادی الکترون دارد.

ذرات بنیادی وجود دارند که خود به خود به ذرات با جرم کمتر واپاشی می‌شوند. یک نمونه از این ذرات میون است که با میانگین طول عمر ۶۹۹۴۲۲۰۰۰۰۰۰۰۰۰۰۰۰۰♠۲٫۲×۱۰^−۶ به یک الکترون، یک نوترینو و یک پادنوترینو واپاشی می‌شود. اما در مباحث نظری الکترون، ذره‌ای پایدار به‌شمار می‌آید: الکترون کم جرم‌ترین ذره با بار الکتریکی غیرصفر است، پس واپاشی آن قانون پایستگی بار را نقض می‌کند. حد پایین تجربی طول‌عمر میانگین الکترون، با ۹۰٪ سطح اطمینان، ۷۰۲۶۴۶۰۰۰۰۰۰۰۰۰۰۰۰۰♠۴٫۶×۱۰^۲۶ سال است.

ویژگی‌های کوانتومی

مانند سایر ذرات، الکترون نیز می‌تواند ویژگی‌های موجی از خود بروز دهد. این ویژگی را دوگانگی موج-ذره می‌نامند و می‌توان از طریق آزمایش دوشکاف آن را نمایش داد.

ماهیت موج-مانند الکترون به آن اجازه می‌دهد که از دو شکاف به‌طور هم‌زمان عبور کند، در حالیکه یک ذره کلاسیک در یک زمان مشخص تنها می‌تواند از یک شکاف عبور کند. در مکانیک کوانتومی ویژگی موج-مانند ذره را می‌توان توسط یک تابع مختلط مقدار به نام تابع موج (ψ)، به زبان ریاضی توصیف نمود. مجذور قدر مطلق این تابع احتمال اینکه یک ذره در نزدیکی یک مکان مشخص مشاهده شود را به‌دست می‌دهد و یک تابع چگالی احتمال است.

نمونه‌ای از یک تابع موج پادتقارنی برای یک وضعیت کوانتومی دو فرمیون یکسان در یک جعبه یک بعدی. اگر ذرات جایشان را با هم عوض کنند، علامت تابع موج قرینه می‌گردد.

الکترون‌ها ذرات یکسانی هستند زیرا نمی‌توان دو الکترون مختلف را برپایه ویژگی‌های فیزیکی ذاتی آن‌ها از یکدیگر متمایز نمود. این در مکانیک کوانتومی بدین معناست که می‌توان جای دو الکترون در حال برهم‌کنش را با یکدیگر عوض نمود، بدون آنکه تغییری در وضعیت کوانتومی سیستم به وجود آید. تابع موج فرمیون‌ها (که شامل الکترون نیز می‌شوند) پادتقارنی است یعنی هرگاه جای الکترون‌ها با هم عوض شود، علامت آن تغییر می‌یابد؛ یعنی (ψ(r_۱, r_۲) = −ψ(r_۲, r_۱ که در آن متغیرهای r_۱ و r_۲ متناظر با الکترون اول و دوم هستند. از آنجا که تعویض علامت، تأثیری در مقدار قدر مطلق ندارد، احتمالات متناظر با این دو حالت یکسان هستند. بوزون‌ها (مانند فوتون) برعکس فرمیون‌ها تابع موج تقارنی دارند.

در مورد امواج پادتقارنی، حل معادله موج برای دو الکترون در حال برهم‌کنش، نتیجه می‌دهد که احتمال اینکه هر دو ذره یک جفت، حالت کوانتومی یکسانی را داشته باشند، صفر است. این اصل بسیاری از ویژگی‌های الکترون را توضیح می‌دهد. این موضع سبب می‌شود که گروه‌های الکترون‌های محدود در یک اتم، به جای اینکه همگی در یک مدار روی هم قرار بگیرند، اوربیتال‌های اتمی مختلفی را در اتم اشغال کنند.

ذرات مجازی

مقالهٔ اصلی: ذره مجازی

با نگاهی ساده‌نگرانه، می‌توان گفت که هر فوتون زمانی را به شکل ترکیبی از یک الکترون مجازی و پادذره آن یعنی پوزیترون مجازی سپری می‌کند که اندکی پس از آن به سرعت یکدیگر را نابود می‌کنند. ترکیب تغییرات انرژی مورد نیاز برای ایجاد این ذرات و زمانی که طی آن وجود دارند، باید پایین‌تر از آستانه مشاهده‌پذیری توصیف شده توسط رابطه عدم قطعیت هایزنبرگ باشد، یعنی

ΔE · Δt ≥ ħ.

در حقیقت انرژی ΔE مورد نیاز برای ایجاد این ذرات مجازی را می‌توان برای بازه زمانی Δt، از خلاء قرض گرفت، با این شرط که حاصل‌ضرب این دو از ثابت پلانک کاهش‌یافته،ħ ≈ ۶۹۸۴۶۶۰۰۰۰۰۰۰۰۰۰۰۰۰♠۶٫۶×۱۰^−۱۶ eV·s بیشتر نباشد. از این رو برای یک الکترون مجازی، Δt حداکثر برابر ۶۹۷۹۱۲۹۹۹۹۹۹۹۹۹۹۹۹۹♠۱٫۳×۱۰^−۲۱ s است.

تصویری شماتیک از یک جفت الکترون-پوزیترون مجازی که به شکل تصادفی در نزدیکی یک الکترون پدید می‌آیند (در قسمت چپ پایین)

در زمانی که یک جفت الکترون-پوزیترون مجازی وجود دارند نیروی کولنی ناشی از میدان الکتریکی اطراف الکترون، باعث می‌شود که یک پوزیترون ایجاد شده جذب الکترون اصلی شود، در حالیکه الکترون ایجاد شده دفع می‌شود. این سبب چیزی می‌شود که به قطبش خلاء مشهور است. در حقیقت خلاء مانند یک رسانا با گذردهی نسبی دی‌الکتریک بیشتر از یک عمل می‌کند؛ بنابراین بار مؤثر یک الکترون در حقیقت کمتر از مقدار واقعی آن است؛ و بار با افزایش فاصله از الکترون کاهش می‌یابد. این پدیده قطبش در سال ۱۹۹۷ توسط شتاب‌دهنده ذرات ژاپنی تریستان مورد تأیید تجربی قرار گرفت. ذرات مجازی سبب ایجاد یک اثر پوششی برای جرم الکترون هم می‌شوند.

همچنین از طریق برهم‌کنش با ذرات مجازی می‌توان اختلاف اندک (در حدود ۰٫۱٪) گشتاور مغناطیسی ذاتی الکترون از مگنتون بور را توضیح داد. همخوانی فوق‌العاده دقیق این اختلاف پیش‌بینی شده با مقدار تعیین‌شده از راه تجربی، یکی از دستاوردهای مهم الکترودینامیک کوانتومی شمرده می‌شود.

پارادوکس ظاهری مشاهده‌شده در مورد یک الکترون نقطه‌ای که دارای تکانه زاویه‌ای و گشتاور مغناطیسی باشد را می‌توان با استفاده از شکل‌گیری فوتون‌های مجازی در میدان الکتریک تولید شده توسط الکترون توضیح داد. این فوتون‌ها باعث می‌شوند که الکترون‌ها به شکل رقصان انتقال یابند که سبب یک حرکت دایره‌ای تقدیمی می‌شود. این حرکت اسپین و گشتاور مغناطیسی الکترون را تولید می‌کند. در اتم‌ها این پیدایش فوتون‌های مجازی تغییر لمب مشاهده‌شده در خطوط طیفی را توضیح می‌دهد.

برهم‌کنش

یک الکترون، میدان الکتریکی ایجاد می‌کند که بر ذرات با بار مثبت مانند پروتون، نیروی جاذبه و بر ذرات دارای بار منفی نیروی دافعه وارد می‌کند. میزان قدرت این نیرو توسط قانون مربع معکوس کولن تعیین می‌شود. الکترون وقتی در حال حرکت باشد، میدان مغناطیسی ایجاد می‌کند. قانون آمپر-ماکسول، ارتباط میان میدان مغناطیسی ایجاد شده با حرکت دسته‌جمعی الکترون‌ها نسبت به یک ناظر(جریان) را توصیف می‌کند. این ویژگی القایی، میدان مغناطیسی مورد نیاز برای چرخش یک موتور الکتریکی فراهم می‌کند. میدان الکترومغناطیسی یک ذره باردار دلخواه در حال حرکت، توسط پتانسیل‌های لینار-ویشرت توصیف می‌شود که حتی وقتی سرعت ذره نزدیک به سرعت نور باشد(نسبیتی) نیز معتبر هستند.

ذره‌ای با بار q (در سمت چپ) در حال حرکت با سرعت v در یک میدان مغناطیسی B است که جهت آن به سوی ناظر است. برای الکترون، علامت q منفی است و بنابراین یک مسیر منحنی به سوی بالا را طی می‌کند.

وقتی الکترونی در درون یک میدان مغناطیسی حرکت می‌کند در معرض نیروی لورنتز قرار می‌گیرد که عمود بر صفحه تعریف شده توسط میدان مغناطیسی و سرعت الکترون وارد می‌شود. این نیروی مرکزگرا سبب مارپیجی شدن مسیر حرکت الکترون درون میدان می‌شود که شعاع این مسیر پیچه‌ای ژیرورادیوس نامیده می‌شود. شتاب ناشی از این حرکت دایره‌ای الکترون را القا می‌کند تا انرژی به شکل تابش سینکروترون آزاد کند. انتشار انرژی به نوبه خود سبب پس‌زنی الکترون می‌شود که با نام نیروی آبراهام-لورنتز-دیراک شناخته می‌شود که اصطکاکی ایجاد می‌کند که باعث کند شدن حرکت الکترون می‌شود. این نیرو ناشی از واکنش به عقب خود میدان الکترون نسبت به خودش است.

در الکترودینامیک کوانتومی، فوتون‌ها واسطه برهم‌کنش میان ذرات هستند. یک الکترون منزوی با سرعت ثابت نمی‌تواند یک فوتون واقعی را جذب یا منتشر کند؛ این کار باعث نقض پایستگی انرژی و تکانه می‌شود. در عوض، فوتون‌های مجازی می‌توانند تکانه را میان دو ذره باردار منتقل کنند. مثلاً این تبادل فوتون‌های مجازی باعث ایجاد نیروی کولنی می‌گردد. انتشار انرژی می‌تواند وقتی که مسیر یک الکترون در حال حرکت توسط ذره بارداری مانند پروتون منحرف می‌شود، اتفاق بیفتد. شتاب گرفتن الکترون باعث انتشار تابش ترمزی می‌شود.

در اینجا تابش ترمزی توسط یک الکترون e منحرف‌شده توسط میدان الکتریکی هسته اتم تولید می‌شود. تغییر انرژی E₂ − E₁ بسامد f فوتون منتشرشده را تعیین می‌کند.

یک برخورد ناکشسان بین یک فوتون (نور) و یک الکترون تکی (آزاد)، پراکندگی کامپتون نامیده می‌شود. چنین تصادمی سبب انتقال تکانه و انرژی میان ذرات می‌شود که باعث تغییر طول موج فوتون به اندازه مقداری که انتقال کامپتون نام دارد، می‌شود. حداکثر مقدار این تغییر طول موج، h/m_ec است که با نام طول موج کامپتون شناخته می‌شود. مقدار آن برای الکترون برابر با ۶۹۸۸۲۴۳۰۰۰۰۰۰۰۰۰۰۰۰♠۲٫۴۳×۱۰^−۱۲ m است. وقتی طول موج نور بلند باشد (مثلاً طول موج نور مرئی ۰٫۷–۰٫۴ میکرومتر است)، میزان تغییر طول موج ناچیز و قابل چشم‌پوشی است. چنین برهم‌کنشی میان نور و الکترون‌های آزاد، پراکندگی تامسون یا پراکندگی خطی تامسون نامیده شده‌است.

قدرت نسبی برهم‌کنش الکترومغناطیس میان دو ذره باردار مانند الکترون و پروتون توسط ثابت ساختار ریز به‌دست می‌آید. این مقدار یک کمیت بدون بعد است که نسبت دو انرژی را نشان می‌دهد: انرژی جاذبه (یا دافعه) الکترواستاتیک در فاصله‌ای به اندازه یک طول موج کامپتون و انرژی سکون بار. مقدار آن برابر است با α ≈ ۶۹۹۷۷۲۹۷۳۵۳۰۰۰۰۰۰۰۰♠۷٫۲۹۷۳۵۳×۱۰^−۳ که تقریباً معادل ^۱⁄_۱۳۷ است.

وقتی الکترون و پوزیترون با هم برخورد می‌کنند، یکدیگر را نابود می‌کنند و دو یا چند فوتون پرتو گاما پدید می‌آورند. اگر تکانه الکترون و پوزیترون قابل چشم‌پوشی باشد، امکان پیدایش یک اتم پوزیترونیوم پیش از آنکه نابودسازی منجر به تولید سه فوتون پرتو گاما (مجموعاً ۱٫۰۲۲ مگا الکترون‌ولت) شود، وجود دارد. از سوی دیگر، فوتون‌های پرانرژی ممکن است در فرایندی به نام جفت‌سازی تبدیل به یک الکترون و یک پوزیترون شوند، البته تنها در صورتی که در نزدیکی یک ذره باردار مانند هسته اتم قرار بگیرد. در نظریه برهم‌کنش الکتروضعیف، مؤلفه چپ‌دست تابع موج الکترون، با الکترون‌نوترینو یک دوگان ایزواسپین ضعیف تشکیل می‌دهد. این بدین معنی است که الکترون‌نوترینوها در برهم‌کنش‌های ضعیف مانند الکترون عمل می‌کنند. هر یک از اعضای این دوگان می‌تواند تحت یک برهم‌کنش جریان باردار، با انتشار یا جذب یک بوزون W به عضو دیگر تبدیل شوند. بار در این واکنش پایسته می‌ماند زیرا بوزون W نیز حامل بار است و میزان تغییرات خالص بار در حین تبدیل صفر است. برهم‌کنش‌های جریان باردار، مسئول پدیده واپاشی بتا در اتم‌های پرتوزا هستند. هر دوی الکترون و الکترون‌نوترینو می‌توانند از طریق مبادله یک بوزون ⁰Z در برهم‌کنش جریان خنثی شرکت کنند و این ویژگی سبب پیدایش پدیده پراکندگی کشسان نوترینو-الکترون می‌شود.

اتم‌ها و مولکول‌ها

چگالی‌های احتمال برای چند اوربیتال نخستین اتم هیدروژن، که برش مقطعی از آن‌ها به تصویر کشیده‌شده است. سطح انرژی یک الکترون مقید مشخص می‌کند که چه اوربیتالی را پر می‌کند، و رنگ نمایش‌دهنده احتمال یافتن الکترون در یک مکان مشخص است.

الکترون را می‌توان از طریق یک نیروی جاذبه کولنی مقید به هسته اتم نمود. سامانه متشکل از یک یا چند الکترون مقید به یک هسته، «اتم» نام دارد. اگر در اتمی تعداد الکترون‌ها با بار الکتریکی هسته برابر نباشد، به آن «یون» گفته می‌شود. رفتار موج-مانند یک الکترون مقید توسط تابعی به نام اوربیتال اتمی توصیف می‌شود. هر اوربیتال مجموعه‌ای از اعداد کوانتومی (مانند انرژی، تکانه زاویه‌ای و تصویر تکانه زاویه‌ای) خاص خود را داراست. و تنها تعداد گسسته‌ای از این اوربیتال‌ها می‌توانند در اطراف هسته وجود داشته‌باشند. بنا بر اصل طرد پاولی، هر اوربیتال می‌تواند حداکثر توسط دو الکترون اشغال شود که باید عدد کوانتومی اسپین آن‌ها از یکدیگر متفاوت باشد.

الکترون‌ها می‌توانند با انتشار یا جذب فوتون بین اوربیتال‌های مختلف منتقل شوند. انرژی فوتون آزاد شده برابر با اختلاف پتانسیل دو اوربیتال خواهد بود. از دیگر روش‌های انتقال اوربیتال الکترون می‌توان به برخورد دادن آن با ذرات و همچنین اثر اوژه اشاره نمود. برای گریختن از اتم، انرژی الکترون باید از انرژی بستگی آن با اتم(انرژی یونش) بیشتر باشد. این اتفاق مثلاً در پدیده فوتوالکتریک روی می‌دهد که در آن یک فوتون تصادفی که انرژی آن از انرژی یونش اتم بیشتر است توسط الکترون جذب می‌شود.

تکانه زاویه‌ای اوربیتالی الکترون کوانتایی است. از آنجا که الکترون باردار است، یک گشتاور مغناطیسی اوربیتالی تولید می‌کنند که متناسب با تکانه زاویه‌ای الکترون است. گشتاور مغناطیسی خالص یک اتم برابر با جمع برداری گشتاورهای مغناطیسی اسپین و اوربیتال همه الکترون‌ها و هسته اتم است. گشتاور مغناطیس هسته دز مقابل الکترون‌ها قابل چشم‌پوشی است. گشتاورهای مغناطیسی دو الکترونی که یک اوربیتال را اشغال کرده‌اند، می‌توانند همدیگر را خنثی کنند.

پیوندهای شیمیایی که میان اتم‌ها روی می‌دهند، نتیجه برهم‌کنش‌های الکترومغناطیسی هستند که توسط مکانیک کوانتوم توصیف می‌شوند. قوی‌ترین پیوندها به اشتراک‌گذاری یا انتقال الکترون بین اتم‌ها شکل می‌گیرند و بدین‌ترتیب امکان شکل‌گیری مولکولها را فراهم می‌کنند. در درون یک مولکول، الکترون‌ها تحت تأثیر هسته‌های اتم‌های متعدد هستند و همان‌طور که در اتم‌های منفرد، اوربیتال‌های اتمی را پر می‌کردند، در مولکول‌ها اوربیتال‌های مولکولی را پر می‌کنند. یکی از فاکتورهای بنیادی در این ساختارهای مولکولی وجود جفت الکترون‌هاست. این الکترون‌ها باید اسپین مخالف داشته‌باشند تا بنا بر اصل طرد پاولی بتوانند با هم یک اوربیتال مولکولی را پرکنند (مانند اتم‌ها). اوربیتال‌های مولکولی مختلف توزیع‌های فضایی متفاوتی از چگالی الکترون دارند. مثلاً در جفت‌های پیوندی (یعنی جفت الکترون‌هایی که در واقع اتم‌ها را به یکدیگر پیوند می‌دهند) با بیشترین احتمال می‌توان الکترون را در حجم کوچکی بین دو هسته یافت، در حالیکه جفت الکترون‌های غیرپیوندی در حجم بزرگی در اطراف هسته‌ها توزیع شده‌اند.

رسانایی

تخلیه بار آذرخش در واقع شاره‌ای از الکترون‌هاست. پتانسیل الکتریکی لازم برای تولید آذرخش ممکن است در نتیجه اثر برق مالشی به‌وجود آمده‌باشد.

چنانچه شمار الکترون‌های جسمی بیشتر یا کمتر از شمار لازم برای ایجاد تعادل با بار مثبت هسته‌های اتم‌هایش باشد، آن جسم دارای بار الکتریکی خالص خواهد بود. اگر جسم دارای فزونی الکترون باشد، گفته می‌شود که جسم دارای بار منفی و اگر کمبود الکترون داشته باشد بار آن را مثبت می‌خوانند. وقتی شمار الکترون‌ها و پروتون‌ها برابر باشد، یکدیگر را خنثی می‌کنند و گفته می‌شود که جسم از نظر الکتریکی خنثی است. در نتیجه پدیده‌ای به نام اثر برق مالشی می‌توان با مالش در اجسام ماکروسکوپی بار الکتریکی ایجاد نمود.

الکترون‌های مستقلی که در حال حرکت در خلاء باشند را الکترون آزاد می‌گویند. الکترون‌ها در فلزات به گونه‌ای رفتار می‌کنند که گویی آزاد هستند. ذرّاتی در فلزات و جامدات دیگر به نام الکترون شناخته می‌شوند، در واقع شبه ذره الکترون هستند که همان بار الکتریکی، اسپین و گشتاور مغناطیسی الکترون‌های واقعی را دارند اما ممکن است جرمشان متفاوت باشد. وقتی الکترون‌های آزاد (چه در خلاء و چه در فلزات) حرکت می‌کنند یک شاره خالص از بار تولید می‌کنند که جریان الکتریکی نامیده می‌شود و باعث ایجاد یک میدان مغناطیسی می‌شود، و بالعکس می‌توان با یک میدان مغناطیسی متغیر، جریان الکتریکی تولید نمود. این برهم‌کنش‌ها را می‌توان با استفاده از معادلات ماکسول به زبان ریاضی بیان نمود.

در هر دمای دلخواه، هر ماده‌ای میزان خاصی از رسانایی الکتریکی دارد که مقدار جریان الکتریکی را در زمانی که پتانسیل برقرار شود، تعیین می‌کند. نمونه رساناهای خوب فلزاتی مانند مس و طلا هستند، در حالیکه شیشه و تفلون رساناهای ضعیفی هستند. در مواد دی‌الکتریک، الکترون‌ها مقید به اتم‌هایشان باقی می‌مانند و ماده به عنوان عایق عمل می‌کند. بیشتر نیم‌رسانا (نیمه‌هادی)ها سطح متغیری از رسانایی بین رسانای کامل و عایق الکتریکی دارند. از سوی دیگر فلزات یک ساختار نوار الکترونیکی دارند که عبارت است از نوارهای الکترونیکی نیمه‌پر. وجود چنین نوارهایی به الکترون‌ها اجازه می‌دهد که به گونه‌ای رفتار کنند که گویا الکترون آزاد یا الکترون نامتمرکز هستند. این الکترون‌ها با اتم خاصی مرتبط نیستند، در نتیجه وقتی یک میدان الکتریکی اعمال می‌شود آزاد هستند که مانند یک گاز (گاز فرمی) در درون ماده حرکت کنند.

به دلیل برخوردهای میان اتم‌ها و الکترون‌ها، سرعت رانش الکترون در یک رسانا در مرتبه میلی‌متر بر ثانیه است، اما سرعت انتشار، یعنی سرعتی که یک تغییر در جریان در یک نقطه از ماده به نقاط دیگر ماده سرایت می‌کند و باعث تغییر جریان در قسمت‌های دیگر می‌شود، معمولاً در حدود ۷۵٪ سرعت نور است. دلیل این موضوع آن است که سیگنال‌های الکتریکی به شکل یک موج منتشر و با سرعتی که وابسته به ثابت دی‌الکتریک ماده است، منتشر می‌شوند.

فلرات رساناهای خوبی برای گرما هستند زیرا الکترون‌های نامتمرکز می‌توانند آزادانه حرکت کنند و انرژی گرمایی را میان اتم‌ها منتقل کنند. اما بر خلاف رسانایی الکتریکی، رسانایی گرمایی یک فلز، تقریباً مستقل از دماست. این موضوع را می‌توان با قانون ویدمان-فرانتس به زبان ریاضی بیان نمود. این قانون چنین می‌گوید که نسبت رسانایی گرمایی به رسانایی الکتریکی متناسب با دماست. بی‌نظمی گرمایی در شبکه فلزی مقاومت الکتریکی ماده را افزایش می‌دهد و بدین ترتیب وابستگی میان جریان الکتریکی و دما ایجاد می‌کند.

وقتی مواد تا دماهای پایین‌تر از دمای بحرانی سرد شوند، دچار تغییر فازی می‌شوند که طی آن تمامی مقاومت خود در برابر جریان الکتریکی را از دست می‌دهند. به این فرایند ابررسانایی گفته می‌شود. در نظریه بی‌سی‌اس، این رفتار توسط جفت‌الکترون‌هایی که وارد بک حالت کوانتومی به نام چگالش بوز-اینشتین می‌شوند، مدل می‌شود. این جفت‌های کوپر، از طریق ارتعاشات شبکه‌ای به نام فونون، حرکتشان را به ماده نزدیکشان مرتبط می‌سازند و بدین ترتیب از برخوردشان با اتم‌ها که منشاء معمول مقاومت الکتریکی است، جلوگیری می‌کنند. (جفت‌های کوپر شعاعی تقریباً برابر با ۱۰۰ نانومتر دارند، بنابراین می‌توانند یکدیگر را همپوشانی کنند) هرچند سازوکار عملکرد ابررساناهای دماهای بالا هنوز مشخص نیست.

الکترون‌های درون جامدات رسانا که خود در واقع شبه‌ذره هستند، وقتی در دماهای نزدیک به صفر مطلق بسیار فشرده شوند، به‌گونه‌ای رفتار می‌کنند که گویا خود به سه شبه‌ذره دیگر تقسیم شده‌اند: اسپینون، اوربیتون و هولون اولی حامل اسپین و گشتاور مغناطیسی است، دومی حامل مکان اوربیتالش و آخری حامل بار الکتریکی است.

حرکت و انرژی

بنا بر نظریه نسبیت خاص اینشتین، وقتی سرعت الکترون به سرعت نور نزدیک می‌شود، از دید یک ناظر، جرم نسبیتی آن افزایش می‌یابد و در نتیجه شتاب دادن به آن از درون چارچوب مرجع ناظر، دشوارتر و دشوارتر می‌شود. سرعت الکترون می‌تواند به سرعت نور در خلاء (c) نزدیک شود اما هرگز به آن نمی‌رسد. هرچند وقتی الکترون‌های نسبیتی (یعنی الکترون‌هایی که با سرعتی نزدیک به نور حرکت می‌کنند) به درون یک رسانه دی‌الکتریک (مانند آب) تزریق شوند که در آن سرعت نور بسیار کمتر از c است، الکترون‌ها در آن رسانه موقتاً سریع‌تر از نور حرکت خواهند کرد. در حین برهم‌کنش با رسانه، نور کم‌سویی تولید می‌کنند که تابش چرنکوف نام دارد.

فاکتور لورنتز به عنوان تابعی از سرعت. با مقدار یک آغاز می‌شود و همچنانکه v به c نزدیک می‌شود به بی‌نهایت میل می‌کند.

آثار نسبیت خاص برپایه کمیتی به نام فاکتور لورنتز بنا شده‌اند که به شکل $\scriptstyle \gamma =1/{\sqrt {1-{v^{2}}/{c^{2}}}}$ تعریف می‌شود و v سرعت ذره است. انرژی جنبشی K_e الکترونی که با سرعت v حرکت می‌کند برابر است با:

$\displaystyle K_{\mathrm {e} }=(\gamma -1)m_{\mathrm {e} }c^{2},$

که در آن m_e جرم الکترون است. شتاب‌دهنده خطی استانفورد قادر است به الکترون تا تقریباً ۵۱ گیگاالکترون‌ولت شتاب دهد. از آنجا که الکترون رفتار موجی دارد، یک طول موج دوبروی به آن نسبت داده می‌شود. این طول موج از رابطه λ_e = h/p به‌دست می‌آید که h ثابت پلانک و p تکانه است. برای ۵۱ گیگا الکترون‌ولت ذکرشده، طول موج در حدود ۶۹۸۳۲۴۰۰۰۰۰۰۰۰۰۰۰۰۰♠۲٫۴×۱۰^−۱۷ m خواهد بود که به اندازه کافی کوچک هست که بتواند در اکتشاف ساختارهای بسیار کوچکتر از اندازه هسته اتم سودمند باشد.

شکل‌گیری

جفت‌سازی ناشی از برخورد یک فوتون با یک هسته اتمی

نظریه مه‌بانگ پذیرفته‌شده‌ترین نظریه علمی برای توضیح مراحل اولیه در تکامل جهان است. در نخستین میلی‌ثانیه پس از مه‌بانگ، دماها بیشتر از ۱۰ میلیارد درجه کلوین بودند و میانگین انرژی فوتون‌ها بیش از یک میلیون الکترون‌ولت بود. این فوتون‌ها به اندازه کافی پرانرژی بودند که بتوانند با یکدیگر واکنش دهند و جفت‌های الکترون و پوزیترون را به‌وجود آورند و به همین شکل جفت‌های پوزیترون-الکترون یکدیگر را نابود کرده و فوتون‌های پرانرژی منتشر می‌کنند:

γ + γ ↔ e+
+ e−

در این مرحله از تکامل جهان بین الکترون‌ها و پوزیترون‌ها و فوتون‌ها تعادلی وجود داشت؛ اما پس از ۱۵ ثانیه دمای جهان پایینتر از حدی بود که شکل‌گیری الکترون-پوزیترون بتواند رخ دهد. بیشتر الکترون‌ها و پوزیترون‌های باقی‌مانده همدیگر را نابود کردند و باعث تابش پرتو گامایی شدند که جهان را مجدداً اندکی گرم‌تر کرد.

به دلایلی که هنوز نامشخص است در حین فرایند لپتون‌زایی شمار الکترون‌ها نسبت به پوزیترون‌ها اندکی فزونی یافت. در نتیجه در حدود یک الکترون از هر یک میلیارد الکترون از فرایند نابودسازی نجات یافت. این مقدار اضافی با مقدار پروتون‌های اضافی نسبت به پادپروتون‌ها در شرایطی به نام عدم تقارن باریون برابر بود و در نتیجه بار خالص جهان صفر بود. پروتون‌ها و نوترون‌های باقی‌مانده، در فرایندی به نام هسته‌زایی (سنتز هسته‌ای) شروع به واکنش با یکدیگر و تشکیل ایزوتوپ‌های هلیم و هیدروژن و مقادیر اندکی لیتیم نمودند. این فرایند پس از حدود ۵ دقیقه به اوج رسید. همه نوترون‌های باقی‌مانده‌ای دچار واپاشی بتای منفی با نیمه عمر ۱۰۰۰ ثانیه شدند و طی این فرایند هرکدام یک پروتون و یک الکترون آزاد کردند:

n → p + e−
+ ν
e

تا ۳۰۰۰۰۰–۴۰۰۰۰۰ سال بعدی، الکترون‌های اضافی پرانرژی‌تر از آن بودند که در بند هسته‌های اتمی بیفتند. در پی آن دوره‌ای به نام دوره بازترکیب آغاز شد که طی آن اتم‌های خنثی شکل گرفتند و جهان در حال انبساط نسبت به تابش شفاف شد.

تقریباً یک میلیون سال پس از مه‌بانگ، نخستین نسل از ستارهها شروع به شکل‌گرفتن نمودند. در درون ستاره‌ها، هسته‌زایی ستاره‌ای منجر به تولید پوزیترون‌ها از همجوشی هسته‌های اتمی می‌شود. این ذرات پادماده بلافاصله توسط الکترون‌ها نابود می‌شوند و پرتو گاما آزاد می‌کنند. نتیجه نهایی این فرایند یک کاهش پایدار در شمار الکترون‌ها و به همان میزان افزایش تعداد نوترون‌هاست، اما فرایند تکامل ستارگان ممکن است منجر به سنتز ایزوتوپ‌های رادیواکتیو شود. ایزوتوپ‌های انتخاب شده ممکن است دچار واپاشی بتای منفی شوند و یک الکترون و یک پادنوترینو از هسته منتشر کنند. مثلاً ایزوتوپ کبالت-۶۰ (⁶⁰Co) واپاشی می‌شود و به نیکل-۶۰ (60
Ni) تبدیل می‌شود.

یک دوش هوای گسترده که در نتیجه یورش یک پرتو کیهانی پرانرژی به جو زمین ایجاد شده‌است.

ستاره‌ای که جرمی بیش از ۲۰ جرم خورشیدی داشته‌باشد، در پایان دوران عمرش ممکن است دچار رمبش گرانشی شود و سیاه‌چاله تشکیل دهد. طبق فیزیک کلاسیک این اجسام پرجرم ستاره‌ای نیروی جاذبه گرانشی اعمال می‌کنند که آنقدر قدرتمند است که هیچ چیز حتی تابش الکترومغناطیسی یارای گریختن ار شعاع شوارتزشیلد را ندارد. اما در فیزیک کوانتومی گمان می‌رود که آثار مکانیک کوانتومی این پتانسیل را دارند که اجازه بدهند تابش هاوکینگ از ان منتشر شود. چنین تصور می‌شود که در افق رویداد این بقایای ستاره‌ای الکترون (و پوزیترون) تولید می‌شود.

وقتی جفت‌های ذرات مجازی (مثلاً الکترون و پروتون) در درون افق رویداد به‌وجود می‌آیند، توزیع فضایی تصادفی این ذرات ممکن است سبب شود که یکی از آن‌ها در خارج از افق رویداد به‌وجود آید. این فرایند را تونل‌زنی کوانتومی می‌گویند، سپس پتانسیل گرانشی این سیاه‌چاله ممکن است انرژی لازم برای تبدیل این ذره مجازی به ذره حقیقی را فراهم کند و باعث تابش آن در فضا شود. در عوض، عضو دیگر این جفت انرژی منفی دریافت می‌کند که باعث کاهش جرم-انرژی سیاه‌چاله می‌شود. با کاهش جرم سرعت تابش هاوکینگ بیشتر می‌شود و باعث تبخیر سیاه‌چاله می‌شود تا سرانجام منفجر شود.

پرتوهای کیهانی ذراتی هستند که با انرژی بالا در فضا حرکت می‌کنند. رویدادهای انرژی به بزرگی ۷۰۰۱۴۸۰۶۵۲۹۴۶۱۰۰۰۰۰♠۳٫۰×۱۰^۲۰ eV ثبت شده‌است. وقتی این ذرات با نوکلئونهای جو زمین برخورد می‌کنند، دوشی از ذرات از جمله پیونها تشکیل می‌شود. بیش از نیمی از پرتوهای کیهانی مشاهده‌شده از زمین از میونها تشکیل می‌شود. میون یکی از اعضای خانواده لپتونهاست که در اتمسفر بالایی بر اثر واپاشی پیون‌ها به وجود می‌آید.

π−
→ μ−
+ ν
μ

میون نیز به نوبه خود می‌تواند به یک الکترون یا پوزیترون واپاشی شود.

μ−
→ e−
+ ν
e + ν
μ

مشاهده

پدیده شفق قطبی که عمدتاً توسط الکترون‌های پرانرژی که در درون جو زمین رسوب می‌کنند، به‌وجود می‌آید

مشاهدات از راه دور الکترون‌ها نیازمند آشکارسازی انرژی تابشی آنهاست. مثلاً در محیط‌های پرانرژی مانند تاج خورشیدی یک ستاره الکترون‌های آزاد تشکیل پلاسمایی می‌دهند که تابش ترمزی منتشر می‌کند. گاز الکترون ممکن است دچار نوسان پلاسما شود. نوسان پلاسما به موج‌هایی گفته‌می‌شود که بر اثر تغیرات هم‌زمان در چگالی الکترون‌ها پدید می‌آیند و این‌ها تولید انرژی می‌کنند که توسط رادیوتلسکوپها قابل ردیابی اسنت.

بسامد یک فوتون متناسب با انرژی آن است. وقتی که یک الکترون مقید بین سطوح مختلف انرژی در اتم انتقال می‌یابد، فوتون‌های با بسامد مشخصی را جذب یا نشر می‌کنند. مثلاً وقتی اتم‌ها تحت تابش از سوی منبعی با طیف گسترده قرار گیرند، خطوط جذبی متمایزی در طیف تابش منتقل‌شده پدیدار می‌شوند. هر عنصر یا مولکولی مجموعه مشخصی از خطوط طیفی خاص خود را دارد؛ مثلاً خطوط طیفی هیدروژن. اندازه‌گیری‌های طیف‌بینی قدرت و پهنای این خطوط، این امکان را فراهم می‌آورد که ترکیب و ویژگی‌های فیزیکی یک ماده را تعیین نمود.

در شرایط آزمایشگاهی، برهم‌کنش‌های الکترون‌های منفرد را می‌توان با استفاده از آشکارسازهای ذرات مشاهده نمود، که امکان اندازه‌گیری ویژگی‌های خاصی مانند انرژی، اسپین و بار را فراهم می‌کند. با پیدایش روش‌هایی مانند دام پل یا دام پنینگ می‌توان درات باردار را در فضای کوچکی برای مدتی طولانی نگاه داشت. این کار امکان اندازه‌گیری دقیق ویژگی‌های ذره را فراهم می‌کند. مثلاً در یک نمونه، با استفاده از دام پنینگ، یک الکترون به مدت ده ماه در محفظه‌ای دربرگرفته‌شد. گشتاور مغناطیسی الکترون در این تلاش، تا ۱۱ رقم دقت تعیین شد که در سال ۱۹۸۰ دقیق‌ترین مقدار در بین مقادیر ثابت‌های فیزیکی به‌شمار می‌آمد.

نخستین تصاویر ویدئویی از توزیع انرژی یک الکترون در فوریه ۲۰۰۸، توسط تیمی در دانشگاه لوند سوئد گرفته‌شد. دانشمندان از فلاش‌های بسیار کوتاه‌مدت نور که به پالس‌های اتوثانیه‌ای مشهورند استفاده کردند که اجازه مشاهده حرکت الکترون را برای نخستین بار ممکن ساخت.

توزیع الکترون در مواد جامد را می‌توان با استفاده از روش طیف‌نگاری ARPES تصویر نمود. این تکنیک از اثر فوتوالکتریک بهره می‌برد تا فضای دوجانبه را اندازه بگیرد. با استفاده از ARPES می‌توان جهت، سرعت و پراکندگی الکترون را در درون مواد تعیین نمود.

کاربردها

پرتوهای ذره‌ای

در حین آزمایش تونل باد ناسا، مدلی از شاتل فضایی هدف پرتوهای الکترونی قرار می‌گیرد که اثر گازهای یونیزه‌کننده در هنگام ورود دوباره به جو را شبیه‌سازی می‌کنند.

از پرتوهای الکترونی در نوعی جوشکاری با نام جوشکاری با تشعشعات الکترونی استفاده می‌شود. با این پرتوها می‌توان چگالی بالایی از انرژی تا ۷۰۰۷۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰♠۱۰^۷ W·cm^−۲ را در نوار باریکی به قطر ۱٫۱–۱٫۳ mm متمرکز نمود و معمولاً نیازی به ماده پرکننده نیز ندارند. این شیوه جوشکاری باید در خلاء انجام شود تا از برهم‌کنش میان الکترون‌ها و مولکول‌های گازها پیش از رسیدن به هدف جلوگیری شود و می‌توان از آن برای جوش دادن مواد رسانایی استفاده نمود که بدون این روش، مواد مناسبی برای جوشکاری نیستند.

طرح نگاری الکترونی (EBL) نام روشی برای قلم‌زنی نیم‌رساناها (نیمه‌هادی‌ها) در دقتهایی در مقیاس‌های کوچکتر از یک میکرومتر است. محدودیت‌های این تکنیک هزینه بالا، کند بودن، نیاز به خلاء برای کار کردن و تمایل الکترون‌ها به پراکندگی در جامدات است. مشکل آخری دقت را به ۱۰ نانومتر محدود می‌کند، به همین دلیل از روش EBL بیشتر برای تولید برخی از مدارهای مجتمع ویژه در تعداد اندک استفاده می‌شود.

از روش پردازش پرتو الکترونی برای پرتوافکنی به مواد جهت تغییر ویژگی‌های فیزیکی یا استریلیزه کردن محصولات غذایی و پزشکی استفاده می‌شود. پرتوهای الکترونی در تابش‌های شدید باعث شاره‌ای شدن یا شبه ذوب شیشه، بدون افزایش قابل توجهی در دمای آن می‌شوند: مثلاً تابش شدید الکترون باعث مرتبه بزرگی کاهش در ویسکوزیته و کاهش انرژی فعال‌سازی آن می‌شود.

در پرتودرمانی، از شتاب‌دهنده‌های خطی ذرات برای تولید پرتوهای الکترونی در درمان تومورهای سطحی استفاده می‌شود. با الکترون درمانی می‌توان بیماری‌های پوستی مانند سرطان سلول پایه‌ای را درمان نمود زیرا الکترون پیش از جذب شدن تنها تا عمق محدودی (معمولاً برای الکترون‌هایی با انرژی ۵–۲۰ مگاالکترون‌ولت، تا عمق ۵ سانتی‌متر) می‌تواند نفوذ کند. از پرتو الکترون می‌توان برای تکمیل درمان در نواحی که مورد تابش پرتو ایکس قرارگرفته‌اند استفاده نمود.

شتاب‌دهنده‌های ذرات از میدان‌های الکتریکی برای راندن الکترون‌ها و پادذرات‌شان در انرژی‌های بالا استفاده می‌کنند. این ذرات در هنگام گذر از میدان‌های مغناطیسی تابش سینکروترون منتشر می‌کنند. وابستگی شدت این تابش به اسپین، باعث قطبش پرتو الکترونی می‌شود (فرایندی که با نام اثر اسکولوف-ترنوف شناخته می‌شود). پرتوهای الکترونی تابیده‌شده می‌تواند در آزمایش‌های مختلفی سودمند واقع شود. تابش سینکروترون همچنین می‌تواند باعث سرد شدن پرتوهای الکترونی شود و بدین ترتیب، پخش تکانه میان ذرات را کاهش دهد. وقتی الکترون و پوزیترون طوری شتاب بگیرند که به انرژی مورد نیاز برسند، پرتوهای الکترونی و پوزیترونی با هم برخورد می‌کنند؛ آشکارسازهای ذرات انرژی‌های منتشره ناشی از برخوردها را که موضوع مطالعه فیزیک ذرات است، مشاهده می‌کنند.

تصویربرداری

پراش الکترونی کم‌انرژی (LEED) شیوه‌ای برای بمباران یک ماده کریستالی با یک پرتو الکترونی موازی‌شده و سپس مشاهده الگوهای پراکندگی حاصله برای تعیین ساختار ماده است. انرژی مورد نیاز برای الکترون معمولاً در محدوده ۲۰–۲۰۰ الکترون‌ولت است. تکنیک پراش الکترونی پرانرژی بازتابی (RHEED) از بازتاب یک پرتو از الکترون‌هایی که از زوایای پایین مختلف پرتاب می‌شوند تا ویژگی‌های سطحی مواد کریستالی را مشخص کند. انرژی پرتو مورد استفاده در این روش معمولاً ۸–۲۰ کیلو الکترون‌ولت و زوایای پرتاب ۱–۴ درجه است.

میکروسکوپ الکترونی یک پرتو متمرکز را به سوی یک نمونه هدایت می‌کند. در نتیجه برهم‌کنش پرتو با ماده، برخی از الکترون‌ها ویژگی‌هایشان مانند حرکت، جهت، زاویه، فاز نسبی و انرژی تغییر می‌کند. میکروسکوپیست‌ها می‌توانند این تغییرات را ثبت کنند تا تصاویر با دقت اتمی از ماده تولید کنند. در نور آبی، دقت میکروسکوپ‌های نوری متعارف به دلیل پراکندگی معمولاً محدود به ۲۰۰ نانومتر است. در مقایسه، میکروسکوپ‌های الکترونی محدود به طول موج دوبروی الکترون هستند. این طول موج مثلاً برای الکترون‌هایی که توسط یک پتانسیل ۱۰۰۰۰۰ ولتی شتاب گرفته‌اند، برابر با ۰٫۰۰۳۷ نانومتر است. میکروسکوپ انحراف-اصلاح‌شده الکترونی عبوری تا دقت ۰٫۰۵ نانومتر را ارائه می‌دهد که برای مشاهده اتم‌ها حتی بیش از حد نیاز است. این ویژگی سبب می‌شود که میکروسکوپ الکترونی وسیله آزمایشگاهی مفیدی برای تصویربرداری با دقت بالا باشد؛ هرجند که میکروسکوپ‌های الکترونی وسایل گرانقیمتی هستند و نگه‌داری آن‌ها پرهزینه است.

دو نوع اصلی از میکروسکوپ‌های الکترونی وجود دارد: عبوری و روبشی. میکروسکوپ‌های الکترونی عبوری مانند پروژکتور آموزشی (اورهد) عمل می‌کنند، بدین صورت که پرتوی از الکترون‌ها را از برشی از ماده عبور می‌دهند و سپس آن را توسط لنزهایی روی اسلاید عکاسی یا یک دستگاه بارجفت‌شده تصویر می‌کنند. میکروسکوپ‌های الکترونی روبشی، مانند یک دستگاه تلویزیون، یک پرتو الکترون بسیار متمرکز را در گستره نمونه مورد مطالعه، روبش شطرنجی (اسکن) می‌کنند تا تصویر را تولید کنند. بزرگنمایی برای هر دونوع میکروسکوپ در محدوده ۲۰۰ تا ۱۰۰۰۰۰۰ برابر یا بیشتر تغییر می‌کند. میکروسکوپ تونلی روبشی، از تونل‌زنی کوانتومی الکترون‌ها از یک نوک تیز فلزی به نمونه مورد مطالعه استفاده می‌کند تا تصاویری با دقت اتمی از سطح آن تهیه کند.

سایر کاربردها

در لیزر الکترون آزاد (FEL) یک پرتو الکترون نسبیتی از میان یک جفت دستگاه نوسان‌ساز می‌گذرد که شامل آرایه‌ای از آهنرباهای دوقطبی هستند که جهت میدان‌هایشان متناوباً تغییر می‌کند. الکترون‌ها تابش سینکروترون منتشر می‌کنند که به شکل همدوسی با همان الکترون‌ها برهم‌کنش می‌کند تا میدان تابش را به شدت در بسامد تشدید تقویت کنند. FEL می‌تواند یک تابش پرتلالو همدوس الکترومغناطیسی، با دامنه گسترده‌ای از بسامدها، از ریزموجها تا پرتو ایکس منتشر کند. این دستگاه می‌توانند در ارتباطات، تولید و پزشکی کاربردهای مختلفی داشته باشند که از جمله آن‌ها می‌توان به جراحی بافت‌های نرم اشاره نمود.

الکترون‌ها نقش بسیار مهمی در لامپهای پرتو کاتدی که به گستردگی در دستگاه‌های نمایش در تجهیزات آزمایشگاهی، نمایشگرهای رایانه‌ها و ست تلویزیون استفاده می‌شوند، دارند. دریک لامپ افزاینده فوتوالکتریک، هر فوتونی که فوتوکاتد برخورد می‌کند بارانی از الکترون‌ها را آغاز می‌کند که پالس جریانی قابل ردیابی تولید می‌کنند. لامپ‌های خلاء از جریان الکترون‌ها برای دستکاری سیگنال‌های الکتریکی استفاده می‌کنند و نقش بسیار مهمی در گسترش فناوری الکترونیک داشتند. هرچند که جای خود را به دستگاه‌های حالت جامد مانند ترانزیستورها دادند.

جستارهای وابسته

• آنیون
• الکتراید
• حباب الکترون
• انتشار اگزوالکترون
• فاکتور جی (فیزیک)
• سامانه‌های تناوبی مولکول‌های کوچک
• اسپینترونیک
• آزمایش اشترن-گرلاخ
• تخلیه بار تاونسند
• اثر زیمان
• فهرست ذرات بنیادی
• لپتون
• ترکیبات الکترونی
• پراکندگی الکترونی
• الکترونگاتیوی
• الکترون‌خواهی
• عدد کوانتومی الکترون
• تابع موج
• اوربیتال
• اوربیتال مولکولی
• مولکول
• اتم
• الکترونگاتیوی

پیوند به بیرون

• تعریف الکترون

الکترون در پروژه‌های خواهر

واژهٔ «الکترون» در ویکی‌واژه
پرونده‌های مرتبط در ویکی‌انبار

For other uses, see Electron (disambiguation).

Electron

Hydrogen atomic orbitals at different energy levels. The more opaque areas are where one is most likely to find an electron at any given time.
Composition	Elementary particle
Statistics	Fermionic
Family	Lepton
Generation	First
Interactions	Gravity, electromagnetic, weak
Symbol	e− , β−
Antiparticle	Positron
Theorized	Richard Laming (1838–1851), G. Johnstone Stoney (1874) and others.
Discovered	J. J. Thomson (1897)
Mass	9.1093837015(28)×10−31 kg 5.48579909070(16)×10−4 Da [1822.8884845(14)]−1 Da 0.51099895000(15) MeV/c2
Mean lifetime	stable ( > 6.6×1028 yr)
Electric charge	−1 e −1.602176634×10−19 C −4.80320451(10)×10−10 esu
Magnetic moment	−1.00115965218091(26) µB
Spin	1 /2
Weak isospin	LH: − 1 /2, RH: 0
Weak hypercharge	LH: −1, RH: −2

The electron is a subatomic particle (denoted by the symbol
e⁻
or
β⁻
or ${\ce {^{0}_{-1}e}}$) whose electric charge is negative one elementary charge. Electrons belong to the first generation of the lepton particle family, and are generally thought to be elementary particles because they have no known components or substructure. The electron's mass is approximately 1836 times smaller than that of the proton. Quantum mechanical properties of the electron include an intrinsic angular momentum (spin) of a half-integer value, expressed in units of the reduced Planck constant, ħ. Being fermions, no two electrons can occupy the same quantum state, in accordance with the Pauli exclusion principle. Like all elementary particles, electrons exhibit properties of both particles and waves: They can collide with other particles and can be diffracted like light. The wave properties of electrons are easier to observe with experiments than those of other particles like neutrons and protons because electrons have a lower mass and hence a longer de Broglie wavelength for a given energy.

Electrons play an essential role in numerous physical phenomena, such as electricity, magnetism, chemistry and thermal conductivity, and they also participate in gravitational, electromagnetic and weak interactions. Since an electron has charge, it has a surrounding electric field, and if that electron is moving relative to an observer, said observer will observe it to generate a magnetic field. Electromagnetic fields produced from other sources will affect the motion of an electron according to the Lorentz force law. Electrons radiate or absorb energy in the form of photons when they are accelerated. Laboratory instruments are capable of trapping individual electrons as well as electron plasma by the use of electromagnetic fields. Special telescopes can detect electron plasma in outer space. Electrons are involved in many applications such as tribology or frictional charging, electrolysis, electrochemistry, battery technologies, electronics, welding, cathode-ray tubes, photoelectricity, photovoltaic solar panels, electron microscopes, radiation therapy, lasers, gaseous ionization detectors and particle accelerators.

Interactions involving electrons with other subatomic particles are of interest in fields such as chemistry and nuclear physics. The Coulomb force interaction between the positive protons within atomic nuclei and the negative electrons without, allows the composition of the two known as atoms. Ionization or differences in the proportions of negative electrons versus positive nuclei changes the binding energy of an atomic system. The exchange or sharing of the electrons between two or more atoms is the main cause of chemical bonding. In 1838, British natural philosopher Richard Laming first hypothesized the concept of an indivisible quantity of electric charge to explain the chemical properties of atoms. Irish physicist George Johnstone Stoney named this charge 'electron' in 1891, and J. J. Thomson and his team of British physicists identified it as a particle in 1897 during the cathode-ray tube experiment. Electrons can also participate in nuclear reactions, such as nucleosynthesis in stars, where they are known as beta particles. Electrons can be created through beta decay of radioactive isotopes and in high-energy collisions, for instance when cosmic rays enter the atmosphere. The antiparticle of the electron is called the positron; it is identical to the electron except that it carries electrical charge of the opposite sign. When an electron collides with a positron, both particles can be annihilated, producing gamma ray photons.

History

See also: History of electromagnetism

Discovery of effect of electric force

The ancient Greeks noticed that amber attracted small objects when rubbed with fur. Along with lightning, this phenomenon is one of humanity's earliest recorded experiences with electricity. In his 1600 treatise De Magnete, the English scientist William Gilbert coined the New Latin term electrica, to refer to those substances with property similar to that of amber which attract small objects after being rubbed. Both electric and electricity are derived from the Latin ēlectrum (also the root of the alloy of the same name), which came from the Greek word for amber, ἤλεκτρον (ēlektron).

Discovery of two kinds of charges

In the early 1700s, French chemist Charles François du Fay found that if a charged gold-leaf is repulsed by glass rubbed with silk, then the same charged gold-leaf is attracted by amber rubbed with wool. From this and other results of similar types of experiments, du Fay concluded that electricity consists of two electrical fluids, vitreous fluid from glass rubbed with silk and resinous fluid from amber rubbed with wool. These two fluids can neutralize each other when combined. American scientist Ebenezer Kinnersley later also independently reached the same conclusion. A decade later Benjamin Franklin proposed that electricity was not from different types of electrical fluid, but a single electrical fluid showing an excess (+) or deficit (−). He gave them the modern charge nomenclature of positive and negative respectively. Franklin thought of the charge carrier as being positive, but he did not correctly identify which situation was a surplus of the charge carrier, and which situation was a deficit.

Between 1838 and 1851, British natural philosopher Richard Laming developed the idea that an atom is composed of a core of matter surrounded by subatomic particles that had unit electric charges. Beginning in 1846, German physicist Wilhelm Eduard Weber theorized that electricity was composed of positively and negatively charged fluids, and their interaction was governed by the inverse square law. After studying the phenomenon of electrolysis in 1874, Irish physicist George Johnstone Stoney suggested that there existed a "single definite quantity of electricity", the charge of a monovalent ion. He was able to estimate the value of this elementary charge e by means of Faraday's laws of electrolysis. However, Stoney believed these charges were permanently attached to atoms and could not be removed. In 1881, German physicist Hermann von Helmholtz argued that both positive and negative charges were divided into elementary parts, each of which "behaves like atoms of electricity".

Stoney initially coined the term electrolion in 1881. Ten years later, he switched to electron to describe these elementary charges, writing in 1894: "... an estimate was made of the actual amount of this most remarkable fundamental unit of electricity, for which I have since ventured to suggest the name electron". A 1906 proposal to change to electrion failed because Hendrik Lorentz preferred to keep electron. The word electron is a combination of the words electric and ion. The suffix -on which is now used to designate other subatomic particles, such as a proton or neutron, is in turn derived from electron.

Discovery of free electrons outside matter

A beam of electrons deflected by a magnetic field into a circle

While studying electrical conductivity in rarefied gases in 1859, the German physicist Julius Plücker observed the radiation emitted from the cathode caused phosphorescent light to appear on the tube wall near the cathode; and the region of the phosphorescent light could be moved by application of a magnetic field. In 1869, Plücker's student Johann Wilhelm Hittorf found that a solid body placed in between the cathode and the phosphorescence would cast a shadow upon the phosphorescent region of the tube. Hittorf inferred that there are straight rays emitted from the cathode and that the phosphorescence was caused by the rays striking the tube walls. In 1876, the German physicist Eugen Goldstein showed that the rays were emitted perpendicular to the cathode surface, which distinguished between the rays that were emitted from the cathode and the incandescent light. Goldstein dubbed the rays cathode rays. Decades of experimental and theoretical research involving cathode rays were important in J. J. Thomson's eventual discovery of electrons.

During the 1870s, the English chemist and physicist Sir William Crookes developed the first cathode-ray tube to have a high vacuum inside. He then showed in 1874 that the cathode rays can turn a small paddle wheel when placed in their path. Therefore, he concluded that the rays carried momentum. Furthermore, by applying a magnetic field, he was able to deflect the rays, thereby demonstrating that the beam behaved as though it were negatively charged. In 1879, he proposed that these properties could be explained by regarding cathode rays as composed of negatively charged gaseous molecules in a fourth state of matter in which the mean free path of the particles is so long that collisions may be ignored.

The German-born British physicist Arthur Schuster expanded upon Crookes's experiments by placing metal plates parallel to the cathode rays and applying an electric potential between the plates. The field deflected the rays toward the positively charged plate, providing further evidence that the rays carried negative charge. By measuring the amount of deflection for a given level of current, in 1890 Schuster was able to estimate the charge-to-mass ratio of the ray components. However, this produced a value that was more than a thousand times greater than what was expected, so little credence was given to his calculations at the time. This is because it was assumed that the charge carriers were much heavier hydrogen or nitrogen atoms. Schuster's estimates would subsequently turn out to be largely correct.

In 1892 Hendrik Lorentz suggested that the mass of these particles (electrons) could be a consequence of their electric charge.

J. J. Thomson

While studying naturally fluorescing minerals in 1896, the French physicist Henri Becquerel discovered that they emitted radiation without any exposure to an external energy source. These radioactive materials became the subject of much interest by scientists, including the New Zealand physicist Ernest Rutherford who discovered they emitted particles. He designated these particles alpha and beta, on the basis of their ability to penetrate matter. In 1900, Becquerel showed that the beta rays emitted by radium could be deflected by an electric field, and that their mass-to-charge ratio was the same as for cathode rays. This evidence strengthened the view that electrons existed as components of atoms.

In 1897, the British physicist J. J. Thomson, with his colleagues John S. Townsend and H. A. Wilson, performed experiments indicating that cathode rays really were unique particles, rather than waves, atoms or molecules as was believed earlier. Thomson made good estimates of both the charge e and the mass m, finding that cathode ray particles, which he called "corpuscles", had perhaps one thousandth of the mass of the least massive ion known: hydrogen. He showed that their charge-to-mass ratio, e/m, was independent of cathode material. He further showed that the negatively charged particles produced by radioactive materials, by heated materials and by illuminated materials were universal. The name electron was adopted for these particles by the scientific community, mainly due to the advocation by G. F. FitzGerald, J. Larmor, and H. A. Lorentz. In the same year Emil Wiechert and Walter Kaufmann also calculated the e/m ratio but they failed short of interpreting their results while J. J. Thomson would subsequently in 1899 give estimates for the electron charge and mass as well: e~6.8×10⁻¹⁰ esu and m~3×10⁻²⁶ g

Robert Millikan

The electron's charge was more carefully measured by the American physicists Robert Millikan and Harvey Fletcher in their oil-drop experiment of 1909, the results of which were published in 1911. This experiment used an electric field to prevent a charged droplet of oil from falling as a result of gravity. This device could measure the electric charge from as few as 1–150 ions with an error margin of less than 0.3%. Comparable experiments had been done earlier by Thomson's team, using clouds of charged water droplets generated by electrolysis, and in 1911 by Abram Ioffe, who independently obtained the same result as Millikan using charged microparticles of metals, then published his results in 1913. However, oil drops were more stable than water drops because of their slower evaporation rate, and thus more suited to precise experimentation over longer periods of time.

Around the beginning of the twentieth century, it was found that under certain conditions a fast-moving charged particle caused a condensation of supersaturated water vapor along its path. In 1911, Charles Wilson used this principle to devise his cloud chamber so he could photograph the tracks of charged particles, such as fast-moving electrons.

Atomic theory

See also: The proton–electron model of the nucleus

The Bohr model of the atom, showing states of an electron with energy quantized by the number n. An electron dropping to a lower orbit emits a photon equal to the energy difference between the orbits.

By 1914, experiments by physicists Ernest Rutherford, Henry Moseley, James Franck and Gustav Hertz had largely established the structure of an atom as a dense nucleus of positive charge surrounded by lower-mass electrons. In 1913, Danish physicist Niels Bohr postulated that electrons resided in quantized energy states, with their energies determined by the angular momentum of the electron's orbit about the nucleus. The electrons could move between those states, or orbits, by the emission or absorption of photons of specific frequencies. By means of these quantized orbits, he accurately explained the spectral lines of the hydrogen atom. However, Bohr's model failed to account for the relative intensities of the spectral lines and it was unsuccessful in explaining the spectra of more complex atoms.

Chemical bonds between atoms were explained by Gilbert Newton Lewis, who in 1916 proposed that a covalent bond between two atoms is maintained by a pair of electrons shared between them. Later, in 1927, Walter Heitler and Fritz London gave the full explanation of the electron-pair formation and chemical bonding in terms of quantum mechanics. In 1919, the American chemist Irving Langmuir elaborated on the Lewis's static model of the atom and suggested that all electrons were distributed in successive "concentric (nearly) spherical shells, all of equal thickness". In turn, he divided the shells into a number of cells each of which contained one pair of electrons. With this model Langmuir was able to qualitatively explain the chemical properties of all elements in the periodic table, which were known to largely repeat themselves according to the periodic law.

In 1924, Austrian physicist Wolfgang Pauli observed that the shell-like structure of the atom could be explained by a set of four parameters that defined every quantum energy state, as long as each state was occupied by no more than a single electron. This prohibition against more than one electron occupying the same quantum energy state became known as the Pauli exclusion principle. The physical mechanism to explain the fourth parameter, which had two distinct possible values, was provided by the Dutch physicists Samuel Goudsmit and George Uhlenbeck. In 1925, they suggested that an electron, in addition to the angular momentum of its orbit, possesses an intrinsic angular momentum and magnetic dipole moment. This is analogous to the rotation of the Earth on its axis as it orbits the Sun. The intrinsic angular momentum became known as spin, and explained the previously mysterious splitting of spectral lines observed with a high-resolution spectrograph; this phenomenon is known as fine structure splitting.

Quantum mechanics

See also: History of quantum mechanics

In his 1924 dissertation Recherches sur la théorie des quanta (Research on Quantum Theory), French physicist Louis de Broglie hypothesized that all matter can be represented as a de Broglie wave in the manner of light. That is, under the appropriate conditions, electrons and other matter would show properties of either particles or waves. The corpuscular properties of a particle are demonstrated when it is shown to have a localized position in space along its trajectory at any given moment. The wave-like nature of light is displayed, for example, when a beam of light is passed through parallel slits thereby creating interference patterns. In 1927, George Paget Thomson discovered the interference effect was produced when a beam of electrons was passed through thin metal foils and by American physicists Clinton Davisson and Lester Germer by the reflection of electrons from a crystal of nickel.

In quantum mechanics, the behavior of an electron in an atom is described by an orbital, which is a probability distribution rather than an orbit. In the figure, the shading indicates the relative probability to "find" the electron, having the energy corresponding to the given quantum numbers, at that point.

De Broglie's prediction of a wave nature for electrons led Erwin Schrödinger to postulate a wave equation for electrons moving under the influence of the nucleus in the atom. In 1926, this equation, the Schrödinger equation, successfully described how electron waves propagated. Rather than yielding a solution that determined the location of an electron over time, this wave equation also could be used to predict the probability of finding an electron near a position, especially a position near where the electron was bound in space, for which the electron wave equations did not change in time. This approach led to a second formulation of quantum mechanics (the first by Heisenberg in 1925), and solutions of Schrödinger's equation, like Heisenberg's, provided derivations of the energy states of an electron in a hydrogen atom that were equivalent to those that had been derived first by Bohr in 1913, and that were known to reproduce the hydrogen spectrum. Once spin and the interaction between multiple electrons were describable, quantum mechanics made it possible to predict the configuration of electrons in atoms with atomic numbers greater than hydrogen.

In 1928, building on Wolfgang Pauli's work, Paul Dirac produced a model of the electron – the Dirac equation, consistent with relativity theory, by applying relativistic and symmetry considerations to the hamiltonian formulation of the quantum mechanics of the electro-magnetic field. In order to resolve some problems within his relativistic equation, Dirac developed in 1930 a model of the vacuum as an infinite sea of particles with negative energy, later dubbed the Dirac sea. This led him to predict the existence of a positron, the antimatter counterpart of the electron. This particle was discovered in 1932 by Carl Anderson, who proposed calling standard electrons negatrons and using electron as a generic term to describe both the positively and negatively charged variants.

In 1947, Willis Lamb, working in collaboration with graduate student Robert Retherford, found that certain quantum states of the hydrogen atom, which should have the same energy, were shifted in relation to each other; the difference came to be called the Lamb shift. About the same time, Polykarp Kusch, working with Henry M. Foley, discovered the magnetic moment of the electron is slightly larger than predicted by Dirac's theory. This small difference was later called anomalous magnetic dipole moment of the electron. This difference was later explained by the theory of quantum electrodynamics, developed by Sin-Itiro Tomonaga, Julian Schwinger and Richard Feynman in the late 1940s.

Particle accelerators

With the development of the particle accelerator during the first half of the twentieth century, physicists began to delve deeper into the properties of subatomic particles. The first successful attempt to accelerate electrons using electromagnetic induction was made in 1942 by Donald Kerst. His initial betatron reached energies of 2.3 MeV, while subsequent betatrons achieved 300 MeV. In 1947, synchrotron radiation was discovered with a 70 MeV electron synchrotron at General Electric. This radiation was caused by the acceleration of electrons through a magnetic field as they moved near the speed of light.

With a beam energy of 1.5 GeV, the first high-energy particle collider was ADONE, which began operations in 1968. This device accelerated electrons and positrons in opposite directions, effectively doubling the energy of their collision when compared to striking a static target with an electron. The Large Electron–Positron Collider (LEP) at CERN, which was operational from 1989 to 2000, achieved collision energies of 209 GeV and made important measurements for the Standard Model of particle physics.

Confinement of individual electrons

Individual electrons can now be easily confined in ultra small (L = 20 nm, W = 20 nm) CMOS transistors operated at cryogenic temperature over a range of −269 °C (4 K) to about −258 °C (15 K). The electron wavefunction spreads in a semiconductor lattice and negligibly interacts with the valence band electrons, so it can be treated in the single particle formalism, by replacing its mass with the effective mass tensor.

Characteristics

Classification

Standard Model of elementary particles. The electron (symbol e) is on the left.

In the Standard Model of particle physics, electrons belong to the group of subatomic particles called leptons, which are believed to be fundamental or elementary particles. Electrons have the lowest mass of any charged lepton (or electrically charged particle of any type) and belong to the first-generation of fundamental particles. The second and third generation contain charged leptons, the muon and the tau, which are identical to the electron in charge, spin and interactions, but are more massive. Leptons differ from the other basic constituent of matter, the quarks, by their lack of strong interaction. All members of the lepton group are fermions, because they all have half-odd integer spin; the electron has spin 1/2.

Fundamental properties

The invariant mass of an electron is approximately 9.109×10⁻³¹ kilograms, or 5.489×10⁻⁴ atomic mass units. Due to mass–energy equivalence, this corresponds to a rest energy of 0.511 MeV. The ratio between the mass of a proton and that of an electron is about 1836. Astronomical measurements show that the proton-to-electron mass ratio has held the same value, as is predicted by the Standard Model, for at least half the age of the universe.

Electrons have an electric charge of −1.602176634×10⁻¹⁹ coulombs, which is used as a standard unit of charge for subatomic particles, and is also called the elementary charge. Within the limits of experimental accuracy, the electron charge is identical to the charge of a proton, but with the opposite sign. As the symbol e is used for the elementary charge, the electron is commonly symbolized by
e⁻
, where the minus sign indicates the negative charge. The positron is symbolized by
e⁺
because it has the same properties as the electron but with a positive rather than negative charge.

The electron has an intrinsic angular momentum or spin of 1/2. This property is usually stated by referring to the electron as a spin-1/2 particle. For such particles the spin magnitude is ħ/2, while the result of the measurement of a projection of the spin on any axis can only be ±ħ/2. In addition to spin, the electron has an intrinsic magnetic moment along its spin axis. It is approximately equal to one Bohr magneton, which is a physical constant equal to 9.27400915(23)×10⁻²⁴ joules per tesla. The orientation of the spin with respect to the momentum of the electron defines the property of elementary particles known as helicity.

The electron has no known substructure. Nevertheless, in condensed matter physics, spin–charge separation can occur in some materials. In such cases, electrons 'split' into three independent particles, the spinon, the orbiton and the holon (or chargon). The electron can always be theoretically considered as a bound state of the three, with the spinon carrying the spin of the electron, the orbiton carrying the orbital degree of freedom and the chargon carrying the charge, but in certain conditions they can behave as independent quasiparticles.

The issue of the radius of the electron is a challenging problem of modern theoretical physics. The admission of the hypothesis of a finite radius of the electron is incompatible to the premises of the theory of relativity. On the other hand, a point-like electron (zero radius) generates serious mathematical difficulties due to the self-energy of the electron tending to infinity. Observation of a single electron in a Penning trap suggests the upper limit of the particle's radius to be 10⁻²² meters. The upper bound of the electron radius of 10⁻¹⁸ meters can be derived using the uncertainty relation in energy. There is also a physical constant called the "classical electron radius", with the much larger value of 2.8179×10⁻¹⁵ m, greater than the radius of the proton. However, the terminology comes from a simplistic calculation that ignores the effects of quantum mechanics; in reality, the so-called classical electron radius has little to do with the true fundamental structure of the electron.

There are elementary particles that spontaneously decay into less massive particles. An example is the muon, with a mean lifetime of 2.2×10⁻⁶ seconds, which decays into an electron, a muon neutrino and an electron antineutrino. The electron, on the other hand, is thought to be stable on theoretical grounds: the electron is the least massive particle with non-zero electric charge, so its decay would violate charge conservation. The experimental lower bound for the electron's mean lifetime is 6.6×10²⁸ years, at a 90% confidence level.

Quantum properties

As with all particles, electrons can act as waves. This is called the wave–particle duality and can be demonstrated using the double-slit experiment.

The wave-like nature of the electron allows it to pass through two parallel slits simultaneously, rather than just one slit as would be the case for a classical particle. In quantum mechanics, the wave-like property of one particle can be described mathematically as a complex-valued function, the wave function, commonly denoted by the Greek letter psi (ψ). When the absolute value of this function is squared, it gives the probability that a particle will be observed near a location—a probability density.

Example of an antisymmetric wave function for a quantum state of two identical fermions in a 1-dimensional box. If the particles swap position, the wave function inverts its sign.

Electrons are identical particles because they cannot be distinguished from each other by their intrinsic physical properties. In quantum mechanics, this means that a pair of interacting electrons must be able to swap positions without an observable change to the state of the system. The wave function of fermions, including electrons, is antisymmetric, meaning that it changes sign when two electrons are swapped; that is, ψ(r₁, r₂) = −ψ(r₂, r₁), where the variables r₁ and r₂ correspond to the first and second electrons, respectively. Since the absolute value is not changed by a sign swap, this corresponds to equal probabilities. Bosons, such as the photon, have symmetric wave functions instead.

In the case of antisymmetry, solutions of the wave equation for interacting electrons result in a zero probability that each pair will occupy the same location or state. This is responsible for the Pauli exclusion principle, which precludes any two electrons from occupying the same quantum state. This principle explains many of the properties of electrons. For example, it causes groups of bound electrons to occupy different orbitals in an atom, rather than all overlapping each other in the same orbit.

Virtual particles

Main article: Virtual particle

In a simplified picture, which often tends to give the wrong idea but may serve to illustrate some aspects, every photon spends some time as a combination of a virtual electron plus its antiparticle, the virtual positron, which rapidly annihilate each other shortly thereafter. The combination of the energy variation needed to create these particles, and the time during which they exist, fall under the threshold of detectability expressed by the Heisenberg uncertainty relation, ΔE · Δt ≥ ħ. In effect, the energy needed to create these virtual particles, ΔE, can be "borrowed" from the vacuum for a period of time, Δt, so that their product is no more than the reduced Planck constant, ħ ≈ 6.6×10⁻¹⁶ eV·s. Thus, for a virtual electron, Δt is at most 1.3×10⁻²¹ s.

A schematic depiction of virtual electron–positron pairs appearing at random near an electron (at lower left)

While an electron–positron virtual pair is in existence, the Coulomb force from the ambient electric field surrounding an electron causes a created positron to be attracted to the original electron, while a created electron experiences a repulsion. This causes what is called vacuum polarization. In effect, the vacuum behaves like a medium having a dielectric permittivity more than unity. Thus the effective charge of an electron is actually smaller than its true value, and the charge decreases with increasing distance from the electron. This polarization was confirmed experimentally in 1997 using the Japanese TRISTAN particle accelerator. Virtual particles cause a comparable shielding effect for the mass of the electron.

The interaction with virtual particles also explains the small (about 0.1%) deviation of the intrinsic magnetic moment of the electron from the Bohr magneton (the anomalous magnetic moment). The extraordinarily precise agreement of this predicted difference with the experimentally determined value is viewed as one of the great achievements of quantum electrodynamics.

The apparent paradox in classical physics of a point particle electron having intrinsic angular momentum and magnetic moment can be explained by the formation of virtual photons in the electric field generated by the electron. These photons can heuristically be thought of as causing the electron to shift about in a jittery fashion (known as zitterbewegung), which results in a net circular motion with precession. This motion produces both the spin and the magnetic moment of the electron. In atoms, this creation of virtual photons explains the Lamb shift observed in spectral lines. The Compton Wavelength shows that near elementary particles such as the electron, the uncertainty of the energy allows for the creation of virtual particles near the electron. This wavelength explains the "static" of virtual particles around elementary particles at a close distance.

Interaction

An electron generates an electric field that exerts an attractive force on a particle with a positive charge, such as the proton, and a repulsive force on a particle with a negative charge. The strength of this force in nonrelativistic approximation is determined by Coulomb's inverse square law. When an electron is in motion, it generates a magnetic field. The Ampère–Maxwell law relates the magnetic field to the mass motion of electrons (the current) with respect to an observer. This property of induction supplies the magnetic field that drives an electric motor. The electromagnetic field of an arbitrary moving charged particle is expressed by the Liénard–Wiechert potentials, which are valid even when the particle's speed is close to that of light (relativistic).

A particle with charge q (at left) is moving with velocity v through a magnetic field B that is oriented toward the viewer. For an electron, q is negative so it follows a curved trajectory toward the top.

When an electron is moving through a magnetic field, it is subject to the Lorentz force that acts perpendicularly to the plane defined by the magnetic field and the electron velocity. This centripetal force causes the electron to follow a helical trajectory through the field at a radius called the gyroradius. The acceleration from this curving motion induces the electron to radiate energy in the form of synchrotron radiation. The energy emission in turn causes a recoil of the electron, known as the Abraham–Lorentz–Dirac Force, which creates a friction that slows the electron. This force is caused by a back-reaction of the electron's own field upon itself.

Here, Bremsstrahlung is produced by an electron e deflected by the electric field of an atomic nucleus. The energy change E₂ − E₁ determines the frequency f of the emitted photon.

Photons mediate electromagnetic interactions between particles in quantum electrodynamics. An isolated electron at a constant velocity cannot emit or absorb a real photon; doing so would violate conservation of energy and momentum. Instead, virtual photons can transfer momentum between two charged particles. This exchange of virtual photons, for example, generates the Coulomb force. Energy emission can occur when a moving electron is deflected by a charged particle, such as a proton. The acceleration of the electron results in the emission of Bremsstrahlung radiation.

An inelastic collision between a photon (light) and a solitary (free) electron is called Compton scattering. This collision results in a transfer of momentum and energy between the particles, which modifies the wavelength of the photon by an amount called the Compton shift. The maximum magnitude of this wavelength shift is h/m_ec, which is known as the Compton wavelength. For an electron, it has a value of 2.43×10⁻¹² m. When the wavelength of the light is long (for instance, the wavelength of the visible light is 0.4–0.7 μm) the wavelength shift becomes negligible. Such interaction between the light and free electrons is called Thomson scattering or linear Thomson scattering.

The relative strength of the electromagnetic interaction between two charged particles, such as an electron and a proton, is given by the fine-structure constant. This value is a dimensionless quantity formed by the ratio of two energies: the electrostatic energy of attraction (or repulsion) at a separation of one Compton wavelength, and the rest energy of the charge. It is given by α ≈ 7.297353×10⁻³, which is approximately equal to 1/137.

When electrons and positrons collide, they annihilate each other, giving rise to two or more gamma ray photons. If the electron and positron have negligible momentum, a positronium atom can form before annihilation results in two or three gamma ray photons totalling 1.022 MeV. On the other hand, a high-energy photon can transform into an electron and a positron by a process called pair production, but only in the presence of a nearby charged particle, such as a nucleus.

In the theory of electroweak interaction, the left-handed component of electron's wavefunction forms a weak isospin doublet with the electron neutrino. This means that during weak interactions, electron neutrinos behave like electrons. Either member of this doublet can undergo a charged current interaction by emitting or absorbing a
W
and be converted into the other member. Charge is conserved during this reaction because the W boson also carries a charge, canceling out any net change during the transmutation. Charged current interactions are responsible for the phenomenon of beta decay in a radioactive atom. Both the electron and electron neutrino can undergo a neutral current interaction via a
Z⁰
exchange, and this is responsible for neutrino-electron elastic scattering.

Atoms and molecules

Main article: Atom

Probability densities for the first few hydrogen atom orbitals, seen in cross-section. The energy level of a bound electron determines the orbital it occupies, and the color reflects the probability of finding the electron at a given position.

An electron can be bound to the nucleus of an atom by the attractive Coulomb force. A system of one or more electrons bound to a nucleus is called an atom. If the number of electrons is different from the nucleus's electrical charge, such an atom is called an ion. The wave-like behavior of a bound electron is described by a function called an atomic orbital. Each orbital has its own set of quantum numbers such as energy, angular momentum and projection of angular momentum, and only a discrete set of these orbitals exist around the nucleus. According to the Pauli exclusion principle each orbital can be occupied by up to two electrons, which must differ in their spin quantum number.

Electrons can transfer between different orbitals by the emission or absorption of photons with an energy that matches the difference in potential. Other methods of orbital transfer include collisions with particles, such as electrons, and the Auger effect. To escape the atom, the energy of the electron must be increased above its binding energy to the atom. This occurs, for example, with the photoelectric effect, where an incident photon exceeding the atom's ionization energy is absorbed by the electron.

The orbital angular momentum of electrons is quantized. Because the electron is charged, it produces an orbital magnetic moment that is proportional to the angular momentum. The net magnetic moment of an atom is equal to the vector sum of orbital and spin magnetic moments of all electrons and the nucleus. The magnetic moment of the nucleus is negligible compared with that of the electrons. The magnetic moments of the electrons that occupy the same orbital (so called, paired electrons) cancel each other out.

The chemical bond between atoms occurs as a result of electromagnetic interactions, as described by the laws of quantum mechanics. The strongest bonds are formed by the sharing or transfer of electrons between atoms, allowing the formation of molecules. Within a molecule, electrons move under the influence of several nuclei, and occupy molecular orbitals; much as they can occupy atomic orbitals in isolated atoms. A fundamental factor in these molecular structures is the existence of electron pairs. These are electrons with opposed spins, allowing them to occupy the same molecular orbital without violating the Pauli exclusion principle (much like in atoms). Different molecular orbitals have different spatial distribution of the electron density. For instance, in bonded pairs (i.e. in the pairs that actually bind atoms together) electrons can be found with the maximal probability in a relatively small volume between the nuclei. By contrast, in non-bonded pairs electrons are distributed in a large volume around nuclei.

Conductivity

A lightning discharge consists primarily of a flow of electrons. The electric potential needed for lightning can be generated by a triboelectric effect.

If a body has more or fewer electrons than are required to balance the positive charge of the nuclei, then that object has a net electric charge. When there is an excess of electrons, the object is said to be negatively charged. When there are fewer electrons than the number of protons in nuclei, the object is said to be positively charged. When the number of electrons and the number of protons are equal, their charges cancel each other and the object is said to be electrically neutral. A macroscopic body can develop an electric charge through rubbing, by the triboelectric effect.

Independent electrons moving in vacuum are termed free electrons. Electrons in metals also behave as if they were free. In reality the particles that are commonly termed electrons in metals and other solids are quasi-electrons—quasiparticles, which have the same electrical charge, spin, and magnetic moment as real electrons but might have a different mass. When free electrons—both in vacuum and metals—move, they produce a net flow of charge called an electric current, which generates a magnetic field. Likewise a current can be created by a changing magnetic field. These interactions are described mathematically by Maxwell's equations.

At a given temperature, each material has an electrical conductivity that determines the value of electric current when an electric potential is applied. Examples of good conductors include metals such as copper and gold, whereas glass and Teflon are poor conductors. In any dielectric material, the electrons remain bound to their respective atoms and the material behaves as an insulator. Most semiconductors have a variable level of conductivity that lies between the extremes of conduction and insulation. On the other hand, metals have an electronic band structure containing partially filled electronic bands. The presence of such bands allows electrons in metals to behave as if they were free or delocalized electrons. These electrons are not associated with specific atoms, so when an electric field is applied, they are free to move like a gas (called Fermi gas) through the material much like free electrons.

Because of collisions between electrons and atoms, the drift velocity of electrons in a conductor is on the order of millimeters per second. However, the speed at which a change of current at one point in the material causes changes in currents in other parts of the material, the velocity of propagation, is typically about 75% of light speed. This occurs because electrical signals propagate as a wave, with the velocity dependent on the dielectric constant of the material.

Metals make relatively good conductors of heat, primarily because the delocalized electrons are free to transport thermal energy between atoms. However, unlike electrical conductivity, the thermal conductivity of a metal is nearly independent of temperature. This is expressed mathematically by the Wiedemann–Franz law, which states that the ratio of thermal conductivity to the electrical conductivity is proportional to the temperature. The thermal disorder in the metallic lattice increases the electrical resistivity of the material, producing a temperature dependence for electric current.

When cooled below a point called the critical temperature, materials can undergo a phase transition in which they lose all resistivity to electric current, in a process known as superconductivity. In BCS theory, pairs of electrons called Cooper pairs have their motion coupled to nearby matter via lattice vibrations called phonons, thereby avoiding the collisions with atoms that normally create electrical resistance. (Cooper pairs have a radius of roughly 100 nm, so they can overlap each other.) However, the mechanism by which higher temperature superconductors operate remains uncertain.

Electrons inside conducting solids, which are quasi-particles themselves, when tightly confined at temperatures close to absolute zero, behave as though they had split into three other quasiparticles: spinons, orbitons and holons. The former carries spin and magnetic moment, the next carries its orbital location while the latter electrical charge.

Motion and energy

According to Einstein's theory of special relativity, as an electron's speed approaches the speed of light, from an observer's point of view its relativistic mass increases, thereby making it more and more difficult to accelerate it from within the observer's frame of reference. The speed of an electron can approach, but never reach, the speed of light in a vacuum, c. However, when relativistic electrons—that is, electrons moving at a speed close to c—are injected into a dielectric medium such as water, where the local speed of light is significantly less than c, the electrons temporarily travel faster than light in the medium. As they interact with the medium, they generate a faint light called Cherenkov radiation.

Lorentz factor as a function of velocity. It starts at value 1 and goes to infinity as v approaches c.

The effects of special relativity are based on a quantity known as the Lorentz factor, defined as $\scriptstyle \gamma =1/{\sqrt {1-{v^{2}}/{c^{2}}}}$ where v is the speed of the particle. The kinetic energy K_e of an electron moving with velocity v is:

$\displaystyle K_{\mathrm {e} }=(\gamma -1)m_{\mathrm {e} }c^{2},$

where m_e is the mass of electron. For example, the Stanford linear accelerator can accelerate an electron to roughly 51 GeV. Since an electron behaves as a wave, at a given velocity it has a characteristic de Broglie wavelength. This is given by λ_e = h/p where h is the Planck constant and p is the momentum. For the 51 GeV electron above, the wavelength is about 2.4×10⁻¹⁷ m, small enough to explore structures well below the size of an atomic nucleus.

Formation

Pair production of an electron and positron, caused by the close approach of a photon with an atomic nucleus. The lightning symbol represents an exchange of a virtual photon, thus an electric force acts. The angle between the particles is very small.

The Big Bang theory is the most widely accepted scientific theory to explain the early stages in the evolution of the Universe. For the first millisecond of the Big Bang, the temperatures were over 10 billion kelvins and photons had mean energies over a million electronvolts. These photons were sufficiently energetic that they could react with each other to form pairs of electrons and positrons. Likewise, positron-electron pairs annihilated each other and emitted energetic photons:

γ
+
γ
↔
e⁺
+
e⁻

An equilibrium between electrons, positrons and photons was maintained during this phase of the evolution of the Universe. After 15 seconds had passed, however, the temperature of the universe dropped below the threshold where electron-positron formation could occur. Most of the surviving electrons and positrons annihilated each other, releasing gamma radiation that briefly reheated the universe.

For reasons that remain uncertain, during the annihilation process there was an excess in the number of particles over antiparticles. Hence, about one electron for every billion electron-positron pairs survived. This excess matched the excess of protons over antiprotons, in a condition known as baryon asymmetry, resulting in a net charge of zero for the universe. The surviving protons and neutrons began to participate in reactions with each other—in the process known as nucleosynthesis, forming isotopes of hydrogen and helium, with trace amounts of lithium. This process peaked after about five minutes. Any leftover neutrons underwent negative beta decay with a half-life of about a thousand seconds, releasing a proton and electron in the process,

n
→
p
+
e⁻
+
ν
_e

For about the next 300000–400000 years, the excess electrons remained too energetic to bind with atomic nuclei. What followed is a period known as recombination, when neutral atoms were formed and the expanding universe became transparent to radiation.

Roughly one million years after the big bang, the first generation of stars began to form. Within a star, stellar nucleosynthesis results in the production of positrons from the fusion of atomic nuclei. These antimatter particles immediately annihilate with electrons, releasing gamma rays. The net result is a steady reduction in the number of electrons, and a matching increase in the number of neutrons. However, the process of stellar evolution can result in the synthesis of radioactive isotopes. Selected isotopes can subsequently undergo negative beta decay, emitting an electron and antineutrino from the nucleus. An example is the cobalt-60 (⁶⁰Co) isotope, which decays to form nickel-60 (⁶⁰
Ni
).

An extended air shower generated by an energetic cosmic ray striking the Earth's atmosphere

At the end of its lifetime, a star with more than about 20 solar masses can undergo gravitational collapse to form a black hole. According to classical physics, these massive stellar objects exert a gravitational attraction that is strong enough to prevent anything, even electromagnetic radiation, from escaping past the Schwarzschild radius. However, quantum mechanical effects are believed to potentially allow the emission of Hawking radiation at this distance. Electrons (and positrons) are thought to be created at the event horizon of these stellar remnants.

When a pair of virtual particles (such as an electron and positron) is created in the vicinity of the event horizon, random spatial positioning might result in one of them to appear on the exterior; this process is called quantum tunnelling. The gravitational potential of the black hole can then supply the energy that transforms this virtual particle into a real particle, allowing it to radiate away into space. In exchange, the other member of the pair is given negative energy, which results in a net loss of mass-energy by the black hole. The rate of Hawking radiation increases with decreasing mass, eventually causing the black hole to evaporate away until, finally, it explodes.

Cosmic rays are particles traveling through space with high energies. Energy events as high as 3.0×10²⁰ eV have been recorded. When these particles collide with nucleons in the Earth's atmosphere, a shower of particles is generated, including pions. More than half of the cosmic radiation observed from the Earth's surface consists of muons. The particle called a muon is a lepton produced in the upper atmosphere by the decay of a pion.

π⁻
→
μ⁻
+
ν
_μ

A muon, in turn, can decay to form an electron or positron.

μ⁻
→
e⁻
+
ν
_e +
ν
_μ

Observation

Aurorae are mostly caused by energetic electrons precipitating into the atmosphere.

Remote observation of electrons requires detection of their radiated energy. For example, in high-energy environments such as the corona of a star, free electrons form a plasma that radiates energy due to Bremsstrahlung radiation. Electron gas can undergo plasma oscillation, which is waves caused by synchronized variations in electron density, and these produce energy emissions that can be detected by using radio telescopes.

The frequency of a photon is proportional to its energy. As a bound electron transitions between different energy levels of an atom, it absorbs or emits photons at characteristic frequencies. For instance, when atoms are irradiated by a source with a broad spectrum, distinct dark lines appear in the spectrum of transmitted radiation in places where the corresponding frequency is absorbed by the atom's electrons. Each element or molecule displays a characteristic set of spectral lines, such as the hydrogen spectral series. When detected, spectroscopic measurements of the strength and width of these lines allow the composition and physical properties of a substance to be determined.

In laboratory conditions, the interactions of individual electrons can be observed by means of particle detectors, which allow measurement of specific properties such as energy, spin and charge. The development of the Paul trap and Penning trap allows charged particles to be contained within a small region for long durations. This enables precise measurements of the particle properties. For example, in one instance a Penning trap was used to contain a single electron for a period of 10 months. The magnetic moment of the electron was measured to a precision of eleven digits, which, in 1980, was a greater accuracy than for any other physical constant.

The first video images of an electron's energy distribution were captured by a team at Lund University in Sweden, February 2008. The scientists used extremely short flashes of light, called attosecond pulses, which allowed an electron's motion to be observed for the first time.

The distribution of the electrons in solid materials can be visualized by angle-resolved photoemission spectroscopy (ARPES). This technique employs the photoelectric effect to measure the reciprocal space—a mathematical representation of periodic structures that is used to infer the original structure. ARPES can be used to determine the direction, speed and scattering of electrons within the material.

Plasma applications

Particle beams

During a NASA wind tunnel test, a model of the Space Shuttle is targeted by a beam of electrons, simulating the effect of ionizing gases during re-entry.

Electron beams are used in welding. They allow energy densities up to 10⁷ W·cm⁻² across a narrow focus diameter of 0.1–1.3 mm and usually require no filler material. This welding technique must be performed in a vacuum to prevent the electrons from interacting with the gas before reaching their target, and it can be used to join conductive materials that would otherwise be considered unsuitable for welding.

Electron-beam lithography (EBL) is a method of etching semiconductors at resolutions smaller than a micrometer. This technique is limited by high costs, slow performance, the need to operate the beam in the vacuum and the tendency of the electrons to scatter in solids. The last problem limits the resolution to about 10 nm. For this reason, EBL is primarily used for the production of small numbers of specialized integrated circuits.

Electron beam processing is used to irradiate materials in order to change their physical properties or sterilize medical and food products. Electron beams fluidise or quasi-melt glasses without significant increase of temperature on intensive irradiation: e.g. intensive electron radiation causes a many orders of magnitude decrease of viscosity and stepwise decrease of its activation energy.

Linear particle accelerators generate electron beams for treatment of superficial tumors in radiation therapy. Electron therapy can treat such skin lesions as basal-cell carcinomas because an electron beam only penetrates to a limited depth before being absorbed, typically up to 5 cm for electron energies in the range 5–20 MeV. An electron beam can be used to supplement the treatment of areas that have been irradiated by X-rays.

Particle accelerators use electric fields to propel electrons and their antiparticles to high energies. These particles emit synchrotron radiation as they pass through magnetic fields. The dependency of the intensity of this radiation upon spin polarizes the electron beam—a process known as the Sokolov–Ternov effect. Polarized electron beams can be useful for various experiments. Synchrotron radiation can also cool the electron beams to reduce the momentum spread of the particles. Electron and positron beams are collided upon the particles' accelerating to the required energies; particle detectors observe the resulting energy emissions, which particle physics studies .

Imaging

Low-energy electron diffraction (LEED) is a method of bombarding a crystalline material with a collimated beam of electrons and then observing the resulting diffraction patterns to determine the structure of the material. The required energy of the electrons is typically in the range 20–200 eV. The reflection high-energy electron diffraction (RHEED) technique uses the reflection of a beam of electrons fired at various low angles to characterize the surface of crystalline materials. The beam energy is typically in the range 8–20 keV and the angle of incidence is 1–4°.

The electron microscope directs a focused beam of electrons at a specimen. Some electrons change their properties, such as movement direction, angle, and relative phase and energy as the beam interacts with the material. Microscopists can record these changes in the electron beam to produce atomically resolved images of the material. In blue light, conventional optical microscopes have a diffraction-limited resolution of about 200 nm. By comparison, electron microscopes are limited by the de Broglie wavelength of the electron. This wavelength, for example, is equal to 0.0037 nm for electrons accelerated across a 100,000-volt potential. The Transmission Electron Aberration-Corrected Microscope is capable of sub-0.05 nm resolution, which is more than enough to resolve individual atoms. This capability makes the electron microscope a useful laboratory instrument for high resolution imaging. However, electron microscopes are expensive instruments that are costly to maintain.

Two main types of electron microscopes exist: transmission and scanning. Transmission electron microscopes function like overhead projectors, with a beam of electrons passing through a slice of material then being projected by lenses on a photographic slide or a charge-coupled device. Scanning electron microscopes rasteri a finely focused electron beam, as in a TV set, across the studied sample to produce the image. Magnifications range from 100× to 1,000,000× or higher for both microscope types. The scanning tunneling microscope uses quantum tunneling of electrons from a sharp metal tip into the studied material and can produce atomically resolved images of its surface.

Other applications

In the free-electron laser (FEL), a relativistic electron beam passes through a pair of undulators that contain arrays of dipole magnets whose fields point in alternating directions. The electrons emit synchrotron radiation that coherently interacts with the same electrons to strongly amplify the radiation field at the resonance frequency. FEL can emit a coherent high-brilliance electromagnetic radiation with a wide range of frequencies, from microwaves to soft X-rays. These devices are used in manufacturing, communication, and in medical applications, such as soft tissue surgery.

Electrons are important in cathode-ray tubes, which have been extensively used as display devices in laboratory instruments, computer monitors and television sets. In a photomultiplier tube, every photon striking the photocathode initiates an avalanche of electrons that produces a detectable current pulse. Vacuum tubes use the flow of electrons to manipulate electrical signals, and they played a critical role in the development of electronics technology. However, they have been largely supplanted by solid-state devices such as the transistor.

See also

• Anyon
• Beta radiation
• Electride
• Electron bubble
• Exoelectron emission
• g-factor
• Lepton
• List of particles
• One-electron universe
• Periodic systems of small molecules
• Spintronics
• Stern–Gerlach experiment
• Townsend discharge
• Zeeman effect