تونل‌زنی کوانتومی

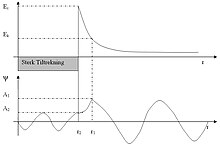
تونل‌زنی کوانتومی (به انگلیسی: Quantum tunneling)‏اشاره به فرایند کوانتومی تونل زنی ذره در طول یک سد -که از نظر کلاسیک ذره قادر به عبور از آن نیست- دارد. این اتفاق مهم در چندین پدیده فیزیکی دیده می شود. برای مثال، در واکنش های هسته ای که در ستارگان رشته اصلی(به انگلیسی: main sequencestars)‏مثل خورشید اتفاق می افتد، به چشم می خورد. همچنین کاربردهای مهمی در وسایل مدرن و جدید مانند دیود تونلی دارد. این پدیده در اوایل قرن بیستم پیش بینی شده بود و در اواسط همین قرن به عنوان یک پدیده کلی فیزیکی پذیزفته شد. تونل زنی معمولا با عنوان اصل عدم قطعیت هایزنبرگ توضیح داده می شود. در واقع مفاهیم مکانیک کوانتومی حول این پدیده می باشند، و می توان گفت تونل زنی کوانتومی یکی از تعاریف ویژگی های مکانیک کوانتومی و خاصیت دوگانگی موج – ذره در جسم می باشد.

تاریخچه

تونل زنی کوانتومی در ابتدا با مطالعه تابش گسترش یافت و در سال 1896 توسط Henri Becquerel کشف شد. مسئله تابش بعدها توسط pierecurie و Marie آزمایش شد، که منجر به دریافت جایزه نوبل فیزیک در سال 1903 توسط آنها شد. Ernest Rutherford وEgon schweidler طبیعت تابش را مطالعه کردند که بعدها توسط Fredrich Kohlrausch به صورت تجربی اثبات شد. بعدها نظریه ی نیمه عمر و عدم امکان پیش گویی واپاشی از کار آنها ارائه شد. Friedrich Hund اولین کسی بود که در سال 1927 وقتی که حالت پایه چاه دوتایی را محاسبه می کرد به پدیده ی تونل زنی توجه کرد.اولین کاربرد این پدیده یک توضیح ریاضی برای واپاشی ذرات آلفا بود که در سال 1928 توسط George Gamow انجام شد. دو محقق دیگر بنام های Ronald Gurney و Edward Condon هم مستقلا این کار راانجام دادند. این دو محقق به طور همزمان معادله ی شرودینگر(به انگلیسی: Schrodinger)‏ را برای یک پتانسیل هسته ای و یک رابطه بین نیم عمر ذره وانرژی تابشی یافتند که مستقیما به احتمال ریاضی تونل زنی وابسته بود. بعد از ارائه ی یک سمینار توسط Gamow، فردی به نام Maxborn کلیت تونل زنی را دریافت. او پی برد که تونل زنی محدود به فیزیک هسته ای نیست بلکه یک نتیجه ی کلی از مکانیک کوانتومی است که در چندین سیستم مختلف ظاهر می شود. اندکی بعد، هر دو گروه موضوع تونل زنی ذرات به درون هسته را مطرح کردند. در پی آن، مطالعه مواد نیمه رسانا و گسترش ترانزیستورها و دیودها منجر به پذیرش تونل زنی الکترون در جامدات، در سال 1957شد. کار Leo Esaki و Ivar Giaver و Brian David Josephson، زوج های کوپر ابررسانایی را پیش بینی کرد که در سال 1973 جایزه نوبل فیزیک را برای آنها به ارمغان آورد.

مقدمه ای بر مفهوم

تونل زنی کوانتومی در یک سد. انرژی ذره تونل زده همان است ولی دامنه کاهش یافته است.

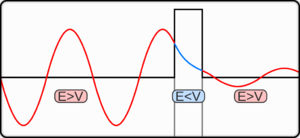
تونل زنی کوانتومی شامل حوزه مکانیک کوانتومی است. آنچه که در مقیاس کوانتومی اتفاق می افتد به طور مشخص قابل مشاهده نیست، اما برای درک بیشتر، در اندازه های ماکروسکوپیک مجسم شده است، که مکانیک کلاسیک به اندازه کافی قادر به توضیح آن است. برای درک این پدیده می توان ذره هایی را که سعی در عبور بین دو چاه پتانسیل دارند را با توپی که دور یک تپه می چرخد مقایسه کرد. مکانیک کوانتومی و مکانیک کلاسیک در این زمینه رفتارهای متفاوتی دارند. مکانیک کلاسیک پیش بینی می کند که ذره ای که انرژی کافی برای عبور کلاسیکی از چاه ندارند قادر به رسیدن به سمت دیگر نیست، پس یک توپ بدون انرژی کافی برای عبور از تپه پس زده شده (بازتاب) و یا در بهترین حالت داخل تپه نفوذ خواهد کرد(جذب). در مکانیک کوانتومی این ذره ها می توانند با احتمال خیلی کم به آن طرف تونل برسند پس می توانند از سد عبور کنند. در این مثال توپ نمی تواند از اطراف خود انرژی بگیرد پس برای تونل زدن در طول دیوار و یا گذر از تپه با پس دادن انرژی، الکترون های بازتابی تولید کرده و در نتیجه انرژی بیشتری نسبت به آنچه در سمت دیگر خواهد داشت، دارد.این تناقض به دلیل رفتار ذره، هم بعنوان ذره و هم بعنوان موج در مکانیک کوانتومی است. یک تفسیر دیگر از این دوگانگی شامل اصل عدم قطعیت هایزنبرگ است که ضمن آن حدی برای دقت در اندازه گیری مکان و تکانه ذره در یک زمان مشخص تعیین شده است. این موضوع دلالت بر این دارد که هیچ جوابی با احتمال دقیقا صفر یا یک وجود ندارد. پس ممکن است یک جواب به بی نهایت برسد. بنابراین احتمال حضور یک ذره در سمت مخالف یک سد غیر صفر است و در این صورت است که ذره ها -بدون هیچ اثری از عبور فیزیکی از سد- ظاهر خواهند شد و با همین احتمال ذره در سمت دیگر با یک فرکانس متناسب، ظاهرمی شوند.

مساله تونل زنی

یک بسته موج الکترونی به یک سد پتانسیل برخورد می کند. به لکه سمت راست توجه کنید که نشان دهنده تونل زنی الکترون هاست.

هر پدیده ای که می توان به عنوان یک سیستم فیزیکی در نظر گرفت، با تابع موج ذره به طور مختصر بیان می شود. اگرچه مسائل در فیزیک کوانتومی متمرکز به تحلیل تابع موج ذره است، با استفاده از فرمول های ریاضی مکانیک کوانتومی نظیر معادله شرودینگر(به انگلیسی: معادله شرودینگر)‏، تایع موج حل خواهد شد واین موضوع مستقیما به چگالی احتمال مکان ذره وابسته است که احتمال حضور ذره در مکان را توصیف می کند. البته در حد سدهای بزرگ احتمال تونل زنی کاهش پیدا میکند(سدهای بلندتر و عریض تر). برای نمونه های ساده تونل زنی سد، مثل سد مستطیلی یک راه حل تحلیلی وجوددارد. معمولا مسائل در واقعیت حتی یک راه حل هم ندارند. پس روش های نیمه کلاسیکی یا شبه کلاسیکی برای راه حل های تقریبی این مسائل، مثل تقریب WKB(به انگلیسی: WKB approximation)‏، گسترش یافتند. احتمال ها ممکن است نتیجه ای با دقت دلخواه باشند.

پدیده های وابسته

چندین پدیده وجود دارد که رفتاری شبیه تونل زنی کوانتومی دارند، پس می توان آنها را دقیقا با تونل زنی توصیف کرد. پدیده هایی مانند جفت شدگی موج ناپایدار (کاربرد معادله موج ماکسول برای نور). این آثار برای سد پتانسیل مستطیلی (به انگلیسی: rectangular potential barrier)‏ شبیه سازی شده اند.در این مثال ها یک ناحیه عبور (به انگلیسی: transmission medium)‏ وجوددارد، که درراستای انتشار موج یا در نزدیکی همان مسیر است و محیط دومی هم وجوددارد که در راستایی قرار دارد که موج به طور متمایز طی می کند.این را می توان به عنوان یک ناحیه ی باریک B بین دو ناحیه باریک A تعریف کرد.حال می توان تحلیل یک سد مستطیلی بوسیله معادله شرودینگر را با آثار دبگر وفق داد، با این شرط که معادله موج دارای جواب موج گذرنده(به انگلیسی: travelling wave)‏ از محیط A باشد اما جواب نمایی حقیقی در محیط B باشد. در اپتیک محیط A خلا است، البته زمانی که محیط B شیشه باشد.در صوت شناسی محیط A می تواند مایع یا گاز باشد و محیط B یک جامد باشد. برای هردو حالت محیط A ناحیه ای از فضاست که انرژی کل ذره بزرگتر از انرژی پتانسیلش است و محیط B سد پتانسیل است. این حالت ها یک موج ورودی دارند و موج برآیند درهردو جهت خواهد بود. هم چنین می توان ناحیه ها و سدهای بیشتری داشت و لزوما نباید این سدها گسسته باشند، تقریب نیز در این مثال ها مفید است.

کاربردها

تونل زنی در سدهایی با ضخامت حدود 3-1نانومتر و کمتر اتفاق می افتد و دلیل بسیاری از پدیده های فیزیکی ماکروسکوپی است.برای مثال تونل زنی در نتایج جریان توان ذاتی و تکنولوژی موبایل دیده می شود.

واپاشی رادیواکتیو

نوشتار اصلی: Radioactive decay‎

واپاشی رادیواکتیو عبارت است از انتشار ذرات و انرژی از هسته ناپایدار یک اتم برای تشکیل یک حالت پایدار.این پدیده در اثر تونل زنی کوانتومی ذره خارج از هسته انجام می شود(تونل زنی ذره درون هسته جاذبه الکترون است)، که اولین کاربرد تونل زنی کوانتومی بود و به اولین تقریب سوق داد.

گسیل سرد

نوشتار اصلی: Semiconductor device‎

گسیل سرد الکترون ها مربوط به فیزیک نیمه رساناها و ابر رساناهاست.این پدیده شبیه پدیده گرمایونی است.

اتصال تونلی

نوشتار اصلی: Tunnel junction‎

یک سد ساده را می توان بااستفاده از دو رسانا و یک عایق نازک ایجاد کرد، که اتصال تونل هستند و مطالعه آن نیازمند تونل زنی کوانتومی است. اتصالات جوزفسون(به انگلیسی: Josephson)‏از تونل زنی کوانتومی و ابررسانایی تعدادی نیمه رسانا بهره گرفته تا اثر جوزفسون را تولید کند. این اثر در اندازه گیری دقیق ولتاژ و میدان مغناطیسی مثل سلول های خورشیدی چند اتصالی، کاربرد دارد.

سازوکار یک دیود تونلی تشدید شده، بر اساس پدیده تونل زنی کوانتومی در یک سد پتانسیل

دیود تونلی

نوشتار اصلی: tunnel diode‎

دیودها قطعات نیمه رسانای الکترونیکی هستند که این امکان را به جریان می دهند که در یک جهت بیشتر از بقیه برقرار شوند. سازوکار این قطعه وابسته به ناحیه ی تهی، بین نیمه رسانای نوع nونوع p می باشد. وقتی اینها کاملا پر شوند،ناحیه تهی می تواند به قدر کافی برای تونل زدن باریک شود. پس از آن اگر بایاس مستقیم کمی اعمال شود جریان حاصل از تونل زنی بسیار قابل توجه خواهد بود، و مقدار حداکثر در جایی است که ولتاژ بایاس طوری است که سطح انرژی در نوار رسانایی p و n یکسان است. همزمان با افزایش ولتاژ بایاس، دیود به طور ایده آل عمل می کند. چون جریان تونل زنی به سرعت از بین می رود، می توان دیود تونلی با ولتاژ متغیر برای کاهش جریان با افزایش ولتاژ، تولید کرد. این ویژگی خاص در چندین مورد کاربرد دارد. دیود تونلی تشدید شده، استفاده از تونل زنی کوانتومی را در روش های مختلف برای دسترسی به نتایج شبیه به این ممکن می سازد.این دیود در جریان زیاد ولتاژ خاصی را ایجاد می کند که ولتاژ تشدید گفته می شود. اینجا یک چاه پتانسیل کوانتومی ایجاد می شود که دارای حداقل سطح انرژی گسسته است. وقتی که این مقدار انرژی بیشتر از انرژی الکترون باشد هیچ تونل زنی اتفاق نمی افتد و دیود در بایاس معکوس است.

ترانزیستور وابسته به میدان تونلی(FET)

یک پروژه تحقیقاتی اروپایی اثبات کرد که FETهایی که در آنها Gate ورودی با تونل زنی کوانتومی بیش از پاشش گرمایی کنترل می شود، ولتاژ Gateرا از 1 ولت تا 0.2 ولت همچنین توان مصرفی را نیز تا 100 برابر کاهش می دهند.

رسانایی کوانتومی

نوشتار اصلی: Classical and quantum conduction‎

می توان با استفاده از تونل زنی کوانتومی پدیده برخورد و رفتار الکترون ها را توضیح داد. وقتی یک بسته موج الکترون آزاد به آرایه ای از چند سد برخورد می کند،قسمت باز تابیده موج با قسمت عبور کرده تداخل می کند، در نتیجه مواردی با صد در صد عبور وجود دارد. این نظریه پیش بینی می کند که اگر هسته با بار مثبت آرایه مستطیلی کاملی تشیل دهد، الکترون های درون فلز به عنوان الکترون های آزاد تونل می زنند و این کار منجر به رسانایی بالا می شود.

میکروسکوپ تونل زنی

نوشتار اصلی: Scanning tunneling microscope‎

میکروسکوپ تونل زنی(STM)که توسط Gred binning وHeinrich rohrer ابداع شده است، امکان تصویر برداری و مطالعه سطح فلزات و بعضی نیمه رساناها را به ما می دهد. این وسیله با بهره گیری از رابطه ی بین تونل زنی کوانتومی با فاصله عمل می کند. وقتی نوک سوزن STM خیلی نزدیک به سطح رسانایی که ولتاژ بایاس دارد قرار گیرد با اندازه گیری جریان الکترون هایی که در حال تونل زدن بین سوزن و سطح رسانا هستند، فاصله بین سوزن و سطح را می توان اندازه گرفت . این کار با استفاده از میله پیزوالکتریک که اندازه اش تغییر می کند، انجام می شود . پس از اعمال ولتاژ در دو سر آن ها ارتفاع نوک را می توان تنظیم کرد و این کار برای تثبیت جریان تونل زنی می باشد.ولتاژ متغیر با زمان که به این میله ها اعمال می شود نیز ثبت می شود که برای تصویر برداری از سطح رسانا به کار برده می شود. STMها دقتی در حدود0.001nm یا حدود 1% ضخامت اتمی دارند.

ریاضیات تونل زنی کوانتومی

این بخش فرمول بندی ریاضی تونل زنی کوانتومی را توصیف می کند.

معادله شرودینگر

معادله مستقل از زمان شرودینگر برای ذره در یک بعد را می توان به صورت زیر نوشت:

$-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \Psi(x) + V(x) \Psi(x) = E \Psi(x)$

یا

$\frac{d^2}{dx^2} \Psi(x) = \frac{2m}{\hbar^2} \left( V(x) - E \right) \Psi(x) \equiv \frac{2m}{\hbar^2} M(x) \Psi(x) ,$

در اینجا $\hbar$ (ثابت پلانک)، m (جرم ذره)، x (نشان دهنده جابجایی در جهت حرکت ذره)،Ψ( تابع موج شرودینگر )،V (انرژی پتانسیل ذره) و E (انرژی ذره) است که وابسته به حرکت ذره در راستای xو M کمیتیاست که با V(x)-E توضیح داده می شود و نام پذیرفته شده ای در فیزیک ندارد. جواب معادله شرودینگر در مقدار های مختلفx و با توجه به اینکه M مثبت است یا منفی متفاوت خواهند بود. اگر M ثابت و منفی باشد،می توان معادله شرودینگر را به صورت زیر نوشت:

$\frac{d^2}{dx^2} \Psi(x) = \frac{2m}{\hbar^2} M(x) \Psi(x) = -k^2 \Psi(x),\;\;\;\;\;\; \mathrm{where} \;\;\; k^2=- \frac{2m}{\hbar^2} M.$

جواب این معادله موج عبوری با ثابت فاز –k یا +k را نشان می دهد .همچنین اگر M ثابت و مثبت باشد، می توان معادله شرودینگر را به صورت زیر نوشت:

$\frac{d^2}{dx^2} \Psi(x) = \frac{2m}{\hbar^2} M(x) \Psi(x) = {\kappa}^2 \Psi(x), \;\;\;\;\;\; \mathrm{where} \;\;\; {\kappa}^2= \frac{2m}{\hbar^2} M.$

جواب های این معادله به صورت نمایی به شکل موج نا پایدار در حال افزایش و کاهش است. وقتی M با مکان تغییر می کند ،بسته به این کهM مثبت است یا منفی، همین تفاوت در رفتار هم رخ می دهد. یعنی اینکه علامت M تعیین تعیین کننده است.M مثبت متناظر با محیط Aو M منفی متناظر با ناحیه Bاست.همچنین این علامت تعیین می کند که جفت شدگی موج ناپایدار می تواند اتفاق بیفتد البته اگر ناحیه باM مثبت بین دو ناحیه باM منفی قرار بگیرد.بنابراین یک سد پتانسیل ایجاد می کند. ریاضیات مربوط با شرایطی کهM با x تغییر می کند سخت و مشکل استبه جز حالت هایی خاص که معمولا در واقیت اتفاق نمی افتد. یک روش تقریبی نیمه کلاسیکی که در کتاب های فیزیک طرح شده است در قسمت بعدی بررسی خواهد شد. یک روش ریاضی کامل و پیچیده در سال 1965 در مقاله ای توسط Froman ذکر شده است. این نظریه در کتاب های فیزیک ثبت نشده است اما تصحیح آن، نتایج کمی اندکی در پی داشت.

تقریب WKB

نوشتار اصلی: WKB approximation‎

تابع موج به صورت نمایی بیان شده است:

$\Psi(x) = e^{\Phi(x)}$, where $\Phi''(x) + \Phi'(x)^2 = \frac{2m}{\hbar^2} \left( V(x) - E \right).$

سپس$\Phi'(x)$به قسمت های موهومی و حقیقی تقسیم شده است:

$\Phi'(x) = A(x) + i B(x)$،

که A و B توابعی با مقدار های حقیقی اند. با جا گذاری معادله دوم در معادله اول و استفاده از این موضوع که قسمت موهومی باید صفر باشد،داریم:

$A'(x) + A(x)^2 - B(x)^2 = \frac{2m}{\hbar^2} \left( V(x) - E \right)$.

برای حل این معادله با استفاده از تقریب نیمه کلاسیکی، هر تابع باید به صورت سری توانی ازħ بسط داده شود.از معادله داریم که سری توانی باید با جمله حداقل از مرتبه1- ħ شروع شود تا قسمت حقیقی معادله را ارضا کند. برای یک حد کلاسیکی خوب شروع با بیشترین توان ثابت پلانک بهتر است که منجر می شود به:

$A(x) = \frac{1}{\hbar} \sum_{k=0}^\infty \hbar^k A_k(x)$

و

$B(x) = \frac{1}{\hbar} \sum_{k=0}^\infty \hbar^k B_k(x)$

با همان فرض جملات کمترین توان داریم:

$A_0(x)^2 - B_0(x)^2 = 2m \left( V(x) - E \right)$

و

$A_0(x) B_0(x) = 0$.

در اینصورت می توان در باره دو حالت نهایی بحث کرد:

حالت اول وقتی دامنه به آهستگی در مقایسه با A(x)=0 تغییر می کند و

$B_0(x) = \pm \sqrt{ 2m \left( E - V(x) \right) }$

که متناظر با حرکت کلاسیکی است. جواب مراتب بعدی بسط نتیجه می دهد:

$\Psi(x) \approx C \frac{ e^{i \int dx \sqrt{\frac{2m}{\hbar^2} \left( E - V(x) \right)} + \theta} }{\sqrt[4]{\frac{2m}{\hbar^2} \left( E - V(x) \right)}}$

حالت دوم وقتی فاز به آهستگی در مقایسه با دامنه B(x)=0 تغییر می کند و

$A_0(x) = \pm \sqrt{ 2m \left( V(x) - E \right) }$

که متناظر با تونل زنی است. جواب مراتب بعدی بسط نتیجه می دهد:

$\Psi(x) \approx \frac{ C_{+} e^{+\int dx \sqrt{\frac{2m}{\hbar^2} \left( V(x) - E \right)}} + C_{-} e^{-\int dx \sqrt{\frac{2m}{\hbar^2} \left( V(x) - E \right)}}}{\sqrt[4]{\frac{2m}{\hbar^2} \left( V(x) - E \right)}}$

در هر دو حالت می توان از مخرج دریافت که هر دو جواب تقریبی همان طور که نشان داده شده،نزدیک نقطه برگشت کلاسیکی هستند $E = V(x)$.دور از چاه پتانسیل ،ذره مثل یک موج نوسان کننده آزاد رفتار می کند.تحت اثر چاه پتانسیل دامنه حرکت ذره به صورت نمایی تغییر می کند. با در نظر گرفتن رفتار در این حدود و نقطه برگشت کلاسیک ، می توان یک جواب کلی ساخت. برای شروع یک نقطه برگشت کلاسیک $x_1$ انتخاب کرده و $\frac{2m}{\hbar^2}\left(V(x)-E\right)$ را به صورت سری توانی حول $x_1$ بسط می دهیم:

$\frac{2m}{\hbar^2}\left(V(x)-E\right) = v_1 (x - x_1) + v_2 (x - x_1)^2 + \cdots$

فقط جمله ی مرتبه ی اول به صورت خطی رفتار می کند:

$\frac{2m}{\hbar^2}\left(V(x)-E\right) = v_1 (x - x_1)$.

با استفاده از این تقریب ،معادله نزدیک $x_1$ به معادله دیفرانسیلی تبدیل می شود. می توان این معادله را با استفاده از (به انگلیسی: Airy function)‏حل کرد.

$\Psi(x) = C_A Ai\left( \sqrt[3]{v_1} (x - x_1) \right) + C_B Bi\left( \sqrt[3]{v_1} (x - x_1) \right)$

با استفاده از این جواب برای همه نقاط برگشت کلاسیکی می توان یک جواب ساخت که جواب های حدی را به هم وصل می کند.ضریب 2 به یک طرف نقطه برگشت کلاسیکی و ضریب 2 به طرف دیگر نقطه برگشت کلاسیکی می دهیم تا با استفاده از این جواب موضعی آنها را به هم وصل کنیم. پس جواب تابع Airy در حدود مناسب با sinx و cosx و تابع نمایی مجانب خواهد بود.رابطه بین$C,\theta$ و $C_{+},C_{-}$ به صورت زیر است.

$C_{+} = \frac{1}{2} C \cos{\left(\theta - \frac{\pi}{4}\right)}$

و

$C_{-} = - C \sin{\left(\theta - \frac{\pi}{4}\right)}$

با ضرایب به دست آمده ،جواب کلی محاسبه می شود.هم چنین ضریب عبور برای ذره که در یک سد پتانسیل تونل می زند به صورت زیر است:

$T = \frac{e^{-2\int_{x_1}^{x_2} dx \sqrt{\frac{2m}{\hbar^2} \left( V(x) - E \right)}}}{ \left( 1 + \frac{1}{4} e^{-2\int_{x_1}^{x_2} dx \sqrt{\frac{2m}{\hbar^2} \left( V(x) - E \right)}} \right)^2}$,

که $x_1,x_2$ دو نقطه عطف کلاسیکی برای حد پتانسیل هستند.