پرش به محتوا

سرعت نور

ویرایش پیوندها
از ویکی‌پدیا، دانشنامهٔ آزاد
برای دیگر کاربردها، سرعت نور (ابهام‌زدایی) را ببینید.
سرعت نور در خلا
فاصله زمین تا خورشید، حدود ۱۵۰ میلیون کیلومتر.
نور خورشید به‌طور میانگین ۸ دقیقه و ۲۰ ثانیه طول می‌کشد تا به زمین برسد.[۱]
مقدارهای دقیق
متر بر ثانیه۲۹۹۷۹۲۴۵۸
واحدهای پلانک۱
مقدارهای تقریبی
کیلومتر بر ثانیه۳۰۰٬۰۰۰
کیلومتر بر ساعت۱٬۰۸۰٬۰۰۰٬۰۰۰
مایل بر ثانیه۱۸۶٬۰۰۰
مایل بر ساعت۶۷۱ میلیون
واحد نجومی بر روز۱۷۳
زمان‌های تقریبی که نور طول می‌کشد طی کند
فاصلهزمان
یک پا۱٫۰ ns
یک متر۳٫۳ ns
یک کیلومتر۳٫۳ μs
یک مایل۵٫۴ μs
از مدار زمین‌ایست‌ور تا زمین۱۱۹ ms
یک دور طول استوای زمین۱۳۴ ms
از ماه تا زمین۱٫۳ s
از خورشید تا زمین (یک واحد نجومی)۸٫۳ دقیقه
از ویجر ۱ تا زمین۱۸٫۱۳ ساعت[Note ۱][۲]
یک پارسک۳٫۲۶ سال
از پروکسیما قنطورس تا زمین۴٫۲۴ سال
از آلفا قنطورس تا زمین۴٫۳۷ سال
از نزدیک‌ترین کهکشان تا زمین (کهکشان سگ کوچک)۲۵٬۰۰۰ سال
طول راه شیری۱۰۰٬۰۰۰ سال
از کهکشان آندرومدا۲٫۵ میلیون سال
از دورترین کهکشان یافت شده تا زمین۱۳ میلیارد سال

سرعت نور در خلأ و ثبات جهانی و دقیقاً برابر ۲۹۹٬۷۹۲٬۴۵۸ متر بر ثانیه است. علت دقت این است که تعریف متر بر اساس سرعت نور و تعریف ثانیه بنا شده‌است.[۳]

این کمیت را در فیزیک و دیگر علوم با حرف c نشان می‌دهند. در محاسبات عادی که دقت زیادی مورد نیاز نیست، سرعت نور را برابر با ۳۰۰٬۰۰۰ کیلومتر بر ثانیه (۳‎×۱۰۸ متر بر ثانیه) در نظر می‌گیرند. مقدار آن تقریباً برابر با ۱۸۶٬۲۸۲ مایل بر ثانیه است. سرعت نور بیشینه سرعتی است که انرژی، ماده و اطلاعات در جهان می‌تواند مسافرت کند. این سرعت همچنان سرعت تمام ذرات بدون جرم و میدان‌های فیزیکی — شامل تابش الکترومغناطیسی که نور نیز جزو آن می‌شود — نیز هست. ذراتی که ذکر شد سرعتشان مستقل چارچوب مرجع است که گسترش این اصل به نسبیت خاص می‌انجامد. همچنین این سرعت در فرمول مشهور هم‌ارزی جرم و انرژی یعنی E = mc² ظاهر می‌شود.[۴]

سرعت نور در اجسام شفاف کمتر از سرعت نور در خلأ است. سرعت نور در خلأ تقسیم بر سرعت نور در آن ماده شفاف (مانند شیشه یا هوا) به عددی بزرگ‌تر از یک می‌انجامد که به آن ضریب شکست (با نماد n نشان می‌دهند) می‌گویند و در فرمول‌های نور هندسی کاربرد دارد. برای مثال ضریب شکست نور مرئی برای شیشه معمولی حدود ۱٫۵ است و بدین معنی است که سرعت نور در شیشه، c / ۱٫۵ ≈ ۲۰۰۰۰۰ km/s است. ضریب شکست نور برای هوا ۱٫۰۰۰۳ (۱٫۰۰۰۳) است که نشان می‌دهد نور در هوا حدود ۹۰ km/s کندتر از c حرکت می‌کند.

برای بسیاری از کاربردها، نور و دیگر امواج الکترومغناطیسی بدون تأخیر جابجا می‌شوند اما برای فواصل زیاد و اندازه‌گیری‌هایی بسیار حساس، سرعت محدود نور اثرات ملموسی دارد. در ارتباطات با کاوشگران فضایی دور ممکن است بین دقایق تا ساعت‌ها طول بکشید تا یک پیام از زمین به کاوشگر برسد یا برگردد. نور ستارگان از سال‌های بسیار گذشته به زمین می‌رسد که اجازه می‌دهد تاریخچه جهان را با بررسی اجسام دور مطالعه کرد. سرعت محدود نور همچنین نظریات حد سرعت رایانه را نیز محدود می‌کند برای اینکه اطلاعاتی که داخل یک کامپیوتر از یک پردازنده به پردازنده دیگر منتقل می‌شود سرعت محدودی خواهد شد.

نخستین بار گالیلئو گالیله سرعت نور را اندازه گرفت. اما مقداری که او به دست آورد بسیار متفاوت‌تر از مقدار واقعی بود. بعدها ستاره‌شناس دانمارکی اوله رومر به کمک گرفت‌های مشتری سرعت نور را تا حد دقیقی اندازه گرفت.

سرعت نور بدون توجه به منبع آن یکسان است. این به این دلیل است که نور، به عنوان شکلی از تابش الکترومغناطیسی، بدون توجه به منبع یا خواص آن، همیشه با همان سرعت در خلاء حرکت می کند. خواه از خورشید، لامپ یا هر منبع دیگری ساطع شود، همیشه با سرعت ثابتی در حدود 299792 کیلومتر در ثانیه حرکت می کند. این یک ویژگی اساسی نور است که توسط آزمایش ها و مشاهدات متعدد در طول سال ها تایید شده است.[۵]

نقش بنیادی در فیزیک

[ویرایش]
همچنین ببینید: نسبیت خاص

سرعت نور مستقل از سرعت ناظر و منبع است.[Note ۲] این ثبات سرعت نور در سال ۱۹۰۵ توسط آلبرت انیشتین بیان شد.[۶] که توسط آزمایش‌های بسیاری صحت آن تأیید شده‌است.[۷][۸] اگرچه در اول مهر ماه ۱۳۹۰ محققان مرکز تحقیقاتی سرن اعلام کردند که حرکت ذرات بنیادی نوترینو با سرعتی بالاتر از سرعت نور را مشاهده کرده‌اند. اما پس از مدت کوتاهی مشخص شد این تضاد به دلیل خطا در آزمایش بوده‌است.[۹][۱۰]

γ از ۱ یعنی زمانی که v برابر صفر است شروع می‌شود و تقریباً برای سرعت‌های پایین مقداری ثابت است اما در نزدیکی سرعت نور به مقدارهای بزرگ میل می‌کند
فاکتور لورنتز γ یک تابعی از سرعت اجسام است؛ که از یک (سرعت=صفر) شروع می‌شود و برای زمانی که سرعت نزدیک سرعت نور شود به بی‌نهایت میل می‌کند.

نسبیت خاص در واقع بررسی قوانین فیزیک برای ناظر و مرجع است برای زمانی که فرض شود سرعت نور وابسته به سرعت منبع یا ناظر نیست.[۱۱][۱۲] یکی از این قوانین این است که سرعت تمام ذرات بدون جرم برابر سرعت نور در خلأ است.

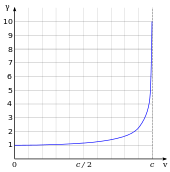
نسبیت خاص اثبات‌های بسیار زیاد آزمایشگاهی دارد.[۱۳] این شامل هم‌ارزی جرم و انرژی (E = mc2)، انقباض لورنتزی (کوتاه‌شدن اجسام در راستای حرکت)، اتساع زمان (کندتر شدن زمان) و افزایش جرم نیز هست. همه این موارد از فاکتور لورنتز به‌دست می‌آیند γ = (۱ − v2/c2)−1/2، که در آن v سرعت جسم است.
تفاوت γ از یک در سرعت‌های کم نسبت به c یعنی تقریباً تمام حرکت‌های روزانه انسان ناچیز است. اما در سرعت‌های نزدیک به نور به مقادیر بسیار بزرگ میل می‌کند. طول جسمی که انقباض لورنتزی دارد و زمانی که در یک متحرک می‌گذرد از تقسیم طول در حالت سکون و زمان در حالت سکون بر فاکتور لورنتز به‌دست می‌آید. اما جرم یک شی متحرک از ضرب فاکتور لورنتز در جرم سکون آن جسم به‌دست می‌آید.

سرعت نور به عنوان حد بالای سرعت

[ویرایش]

بنابر نسبیت خاص، انرژی یک جسم با سرعت v و جرم سکون m با γmc2 به‌دست می‌آید که در آن γ فاکتور لورنتز است. هنگامی که سرعت برابر صفر است فاکتور لورنتز برابر یک بوده و انرژی جسم برابر با E = mc2 است که همان هم‌ارزی جرم و انرژی است. اما هنگامی که سرعت جسم به سرعت نور نزدیک می‌شود این مقدار به سمت بی‌نهایت می‌رود بنابرین برای رساندن سرعت جسمی که جرم غیرصفر دارد به سرعت نور؛ نیاز به بی‌نهایت انرژی است. به همین دلیل سرعت نور، حد بالای سرعت در طبیعت است. این موضوع در تعداد زیادی پژوهش و آزمایش به اثبات رسیده‌است.[۱۴]

انتشار نور

[ویرایش]
شکست نور و تغییر سرعت نور بعد از ورود به یک محیط با ضریب گذردهی متفاوت

در فیزیک کلاسیک، نور به عنوان نوعی موج الکترومغناطیسی توصیف می‌شود. از آنجاکه رفتار میدان الکترومغناطیسی توسط معادلات ماکسول تشریح شده‌است، این معادلات پیش‌بینی می‌کنند که سرعت c با انتشار امواج الکترومغناطیسی (مانند نور) در خلأ را می‌توان با ظرفیت خازنی و القایی خلاء بیان کرد. به بیان دیگر سرعت انتشار نور با ریشه ثابت تراوایی خلأ در ثابت گذردهی خلأ رابطه عکس دارد که در رابطه زیر نمایش داده شده‌است.[۱۵]

در فیزیک نوین، میدان الکترومغناطیسی توسط نظریه الکترودینامیک کوانتومی توصیف می‌شود. در این نظریه، نور توسط تحریک بنیادی (یا کوانتای) میدان الکترومغناطیسی، که فوتون نامیده می‌شود، توصیف می‌شود. در نظریه الکترودینامیک کوانتومی، فوتون‌ها ذرات بدون جرمی هستند که بنابر نسبیت خاص، با سرعت نور در خلأ حرکت می‌کنند.

اثرات عملی محدود بودن

[ویرایش]

سرعت نور به مخابرات مربوط می‌شود: زمان تأخیر مخابرات یک طرفه و رفت و برگشت بزرگتر از صفر است. این از مقیاس‌های کوچک تا نجومی صدق می‌کند. از سوی دیگر، برخی از تکنیک‌ها به سرعت محدود نور بستگی دارند، به عنوان مثال در اندازه‌گیری فاصله.

مقیاس‌های کوچک

[ویرایش]

در ابرکامپیوترها، سرعت نور محدودیتی در سرعت ارسال داده‌ها بین پردازنده‌ها ایجاد می‌کند. اگر یک پردازنده در ۱  گیگاهرتز کار کند، یک سیگنال می‌تواند حداکثر حدود ۳۰ سانتیمتر (۱ فوت) در یک چرخه طی کند؛ بنابراین، پردازنده‌ها باید نزدیک یکدیگر قرار گیرند تا تأخیرهای ارتباطی به حداقل برسد. این می‌تواند باعث ایجاد مشکل در خنک کردن پردازنده‌ها شود. اگر فرکانس‌ها به افزایش ادامه دهند، سرعت نور در نهایت به یک عامل محدود کننده برای طراحی داخلی تراشه‌ها تبدیل می‌شود.

فاصله‌های بزرگ روی زمین

[ویرایش]

با توجه به اینکه محیط استوایی زمین حدود ۴۰۰۷۵ کیلومتر است و c حدود ۳۰۰ هزار کیلومتر بر ثانیه است. کوتاهترین زمان ممکن برای انتقال اطلاعات برای مسافتی حدود نیمی از کره زمین حدود ۶۷ میلی ثانیه است. هنگامی که نور در یک فیبر نوری در سراسر کره زمین در حال حرکت است، زمان انتقال واقعی طولانی‌تر است، بخشی به این دلیل که سرعت نور در فیبر نوری بسته به ضریب شکست آن (n) حدود ۳۵ درصد کندتر است.

پروازهای فضایی و ستاره‌شناسی

[ویرایش]
The diameter of the moon is about one quarter of that of Earth, and their distance is about thirty times the diameter of Earth. A beam of light starts from the Earth and reaches the Moon in about a second and a quarter.
پرتوی از نور در حال حرکت بین زمین و ماه در زمانی که بین آنها طول می‌کشد در حرکت است: ۱٫۲۵۵ ثانیه در فاصله مداری متوسط آنها (سطح به سطح). اندازه نسبی و جدایی سیستم زمین-ماه به مقیاس نشان داده شده‌است.

به‌طور مشابه، ارتباطات بین زمین و فضاپیما آنی نیست. تأخیر مختصری از منبع تا گیرنده وجود دارد که با افزایش فاصله بیشتر محسوس می‌شود. این تأخیر برای ارتباطات بین کنترل زمینی و آپولو ۸، زمانی که اولین فضاپیمای با سرنشین بود که به دور ماه می‌چرخید، قابل توجه بود: برای هر سؤال، ایستگاه کنترل زمینی باید حداقل سه ثانیه برای رسیدن پاسخ منتظر می‌ماند. تأخیر ارتباط بین زمین و مریخ بسته به موقعیت نسبی دو سیاره می‌تواند بین پنج تا بیست دقیقه متغیر باشد. در نتیجه، اگر روباتی در سطح مریخ با مشکلی مواجه شود، کنترل‌کننده‌های انسانی آن حداقل تا پنج دقیقه بعد و احتمالاً تا بیست دقیقه بعد از آن آگاه نمی‌شوند. سپس پنج تا بیست دقیقه دیگر طول می‌کشد تا دستورالعمل سفر از زمین به مریخ برسد.

دریافت نور و سیگنال‌های دیگر از منابع نجومی دور حتی می‌تواند بسیار بیشتر طول بکشد؛ مثلاً ۱۳ میلیارد (13 ‎×۱۰۹ 10 9) سال طول می‌کشد تا نور از کهکشان‌های دور به زمین که در تصاویر میدان فوق‌العاده عمیق هابل مشاهده شده‌است، برسد. عکس‌هایی که امروز گرفته شده‌اند، تصاویری از کهکشان‌ها در زمان ظاهر شدنشان در ۱۳ میلیارد سال پیش ثبت می‌کنند، زمانی که جهان کمتر از یک میلیارد سال سن داشت.[۱۶] این واقعیت که اجرام دورتر به دلیل سرعت محدود نور جوان‌تر به نظر می‌رسند، به اخترشناسان اجازه می‌دهد تا تکامل ستارگان، کهکشان‌ها و خود کیهان را پژوهش کنند.

فواصل نجومی گاهی با سال نوری بیان می‌شود، به ویژه در نشریات و رسانه‌های علمی عامه‌محور. یک سال نوری مسافتی است که نور در یک سال ژولینی، طی می‌کند حدود ۹۴۶۱ میلیارد کیلومتر، یا ۵۸۷۹ میلیارد مایل یا ۰٫۳۰۶۶ پارسک. در ارقام گرد، یک سال نوری نزدیک به ۱۰ تریلیون کیلومتر یا نزدیک به ۶ تریلیون مایل است. پروکسیما قنطورس، نزدیکترین ستاره به زمین پس از خورشید، حدود ۴٫۲ سال نوری فاصله دارد.

اندازه‌گیری فاصله

[ویرایش]

سیستم‌های راداری فاصله تا یک هدف را با زمانی که یک پالس موج رادیویی پس از انعکاس توسط هدف به آنتن رادار بازمی‌گردد اندازه‌گیری می‌کنند: فاصله تا هدف نصف زمان عبور رفت و برگشت ضربدر سرعت نور است. گیرنده سیستم موقعیت‌یاب جهانی (GPS) فاصله خود را تا ماهواره‌های GPS بر اساس مدت زمانی که طول می‌کشد تا سیگنال رادیویی از هر ماهواره برسد را اندازه‌گیری می‌کند و براساس این فاصله‌ها موقعیت خود را محاسبه می‌کند. از آنجایی که نور حدود ۳۰۰٬۰۰۰ کیلومتر بر ثانیه حرکت می‌کند، این اندازه‌گیری‌های کسر کوچکی از ثانیه باید بسیار دقیق باشند. آزمایش فاصله‌سنجی ماه، اخترشناسی راداری و شبکه فضای دوردوست ناسا به ترتیب با اندازه‌گیری زمان‌های عبور رفت و برگشت، فاصله تا ماه، سیارات و فضاپیماها را تعیین می‌کنند.

تجارت فرکانس بالا

[ویرایش]

سرعت نور در معاملات با فرکانس بالا اهمیت پیدا کرده‌است، جایی که معامله‌گران برای کسب مزیت‌های جزئی دنبال ارائه معاملات خود به صرافی‌ها کسری از ثانیه زودتر از سایر معامله‌گران هستند. به عنوان مثال، معامله‌گران به ارتباطات مایکروویو بین مراکز تجاری روی آورده‌اند، به این دلیل که امواج مایکروویو در هوا حرکت می‌کنند و به خاطر بالاتر بودن سرعت نور در هوا، نسبت به سیگنال‌های فیبر نوری ۳۰ تا ۴۰ درصد سریعتر حرکت می‌کنند.

تاریخچه

[ویرایش]
تاریخچه اندازه‌گیری سرعت نور (به km/s)
<۱۶۳۸ گالیلئو گالیله، با استفاده از فانوس بی‌نتیجه[۱۷][۱۸][۱۹]
<1667 آکادمی آزمایش، با استفاده از فانوس نامشخص[۱۹]: 1253 [۲۰]
۱۶۷۵ اوله رومر و کریستیان هویگنس، قمرهای مشتری ۲۲۰۰۰۰[۲۱][۲۲]
۱۷۲۹ جیمز بردلی، انحراف نور ۳۰۱۰۰۰[۲۳]
۱۸۴۹ ایپولیت فیزو، چرخ دندانه‌دار ۳۱۵۰۰۰[۲۳]
۱۸۶۲ لئون فوکو، آینه چرخان ۲۹۸۰۰۰±۵۰۰[۲۳]
۱۹۰۷ روزا و دورسی، ثابت‌های الکترومغناطیسی ۲۹۹۷۱۰±۳۰[۲۴][۲۵]
۱۹۲۶ آلبرت آبراهام مایکلسون، آینه چرخان ۲۹۹۷۹۶±۴[۲۶]
۱۹۵۰ اسن و گوردن اسمیت, نوسانگر کاواکی ۲۹۹۷۹۲٫۵±۳٫۰[۲۷]
۱۹۵۸ کی.دی. فروم، تداخل‌سنجی رادیویی ۲۹۹۷۹۲٫۵۰±۰٫۱۰[۲۸]
۱۹۷۲ اوانسون و دیگران، تداخل‌سنجی لیزر ۲۹۹۷۹۲٫۴۵۶۲±۰٫۰۰۱۱[۲۹]
۱۹۸۳ 17th CGPM, تعریف متر ۲۹۹۷۹۲٫۴۵۸ (دقیقاً)[۳۰]

منابع

[ویرایش]
  1. ↑ Fraser Cain (April 15, 2013). "How long does it take sunlight to reach the Earth?". phys.org (به انگلیسی). Retrieved 9 November 2019.
  2. ↑ "Where Are the Voyagers - NASA Voyager". Voyager - The Interstellar Mission. Jet Propulsion Laboratory, California Istitute of Technology. Retrieved 2011-07-12.
  3. ↑ Penrose, R (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage Books. pp. 410–1. ISBN 978-0-679-77631-4. ... the most accurate standard for the metre is conveniently defined so that there are exactly 299,792,458 of them to the distance travelled by light in a standard second, giving a value for the metre that very accurately matches the now inadequately precise standard metre rule in Paris.
  4. ↑ Uzan, J-P; Leclercq, B (2008). The Natural Laws of the Universe: Understanding Fundamental Constants. Springer. pp. 43–4. ISBN 0-387-73454-6.
  5. ↑ هوش مصنوعی.
  6. ↑ Einstein, A (1905). "Zur Elektrodynamik bewegter Körper" (PDF). سالنامه فیزیک (به آلمانی). 17: 890–921. Archived from the original (PDF) on 29 December 2009. Retrieved 6 September 2011. ترجمه انگلیسی: Perrett, W; Jeffery, GB (tr.); Walker, J. "On the Electrodynamics of Moving Bodies". Fourmilab. Retrieved 2009-11-27.
  7. ↑ Hsu, J-P; Zhang, YZ (2001). Lorentz and Poincaré Invariance. Advanced Series on Theoretical Physical Science. Vol. 8. World Scientific. pp. 543ff. ISBN 9810247214.
  8. ↑ Zhang, YZ (1997). Special Relativity and Its Experimental Foundations. Advanced Series on Theoretical Physical Science. Vol. 4. World Scientific. pp. 172–3. ISBN 9810227493. Archived from the original on 19 May 2012. Retrieved 6 September 2011.
  9. ↑ «کشف تازه ای که قوانین شناخته شده فیزیک را نقض می‌کند». بی‌بی‌سی فارسی. ۱ مهر ۱۳۹۰. دریافت‌شده در ۲ مهر ۱۳۹۰.
  10. ↑ Nick Collins (23 Sep 2011). "Science world in shock after Cern light speed claim" (به انگلیسی). The Daily Telegraph. Archived from the original on 24 September 2011. Retrieved 24 September 2011.
  11. ↑ d'Inverno, R (1992). Introducing Einstein's Relativity. Oxford University Press. pp. 19–20. ISBN 0-19-859686-3.
  12. ↑ Sriranjan, B (2004). "Postulates of the special theory of relativity and their consequences". The Special Theory to Relativity. PHI Learning. pp. 20 ff. ISBN 812031963X.
  13. ↑ Roberts, T; Schleif, S; Dlugosz, JM (2007). "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. University of California, Riverside. Retrieved 2009-11-27.
  14. ↑ Fowler, M (March 2008). "Notes on Special Relativity" (PDF). دانشگاه ویرجینیا. p. 56. Retrieved 2010-05-07.
  15. ↑ «Panofsky, WKH; Phillips, M (1962). Classical Electricity and Magnetism. Addison-Wesley. p. 182. ISBN 978-0-201-05702-7».
  16. ↑ "Hubble Reaches the "Undiscovered Country" of Primeval Galaxies" (Press release). Space Telescope Science Institute. 5 January 2010.
  17. ↑ Galilei, G (1954) [1638]. Dialogues Concerning Two New Sciences. Crew, H; de Salvio A (trans.). Dover Publications. p. 43. ISBN 978-0-486-60099-4. Archived from the original on 30 January 2019. Retrieved 8 April 2021.
  18. ↑ Boyer, CB (1941). "Early Estimates of the Velocity of Light". Isis. 33 (1): 24. doi:10.1086/358523. S2CID 145400212.
  19. ↑ ۱۹٫۰ ۱۹٫۱ Foschi, Renato; Leone, Matteo (2009), "Galileo, measurement of the velocity of light, and the reaction times", Perception, 38 (8): 1251–59, doi:10.1068/p6263, hdl:2318/132957, PMID 19817156, S2CID 11747908
  20. ↑ Magalotti, Lorenzo (2001) [1667], Saggi di Naturali Esperienze fatte nell' Accademia del Cimento (digital, online ed.), Florence: Istituto e Museo di Storia delle Scienze, pp. 265–66, retrieved 2015-09-25
  21. ↑ "Demonstration tovchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences" [Demonstration to the movement of light found by Mr. Römer of the Royal Academy of Sciences] (PDF). Journal des sçavans (به فرانسوی): 233–36. 1676.
    Translated in "A demonstration concerning the motion of light, communicated from Paris, in the Journal des Sçavans, and here made English". Philosophical Transactions of the Royal Society. 12 (136): 893–95. 1677. Bibcode:1677RSPT...12..893.. doi:10.1098/rstl.1677.0024.
    Reproduced in Hutton, C; Shaw, G; Pearson, R, eds. (1809). "On the Motion of Light by M. Romer". The Philosophical Transactions of the Royal Society of London, from Their Commencement in 1665, in the Year 1800: Abridged. Vol. Vol. II. From 1673 to 1682. London: C. & R. Baldwin. pp. 397–98. {{cite book}}: |volume= has extra text (help)
    The account published in Journal des sçavans was based on a report that Rømer read to the French Academy of Sciences in November 1676 (Cohen, 1940, p.  346).
  22. ↑ Huygens, C (1690). Traitée de la Lumière (به فرانسوی). Pierre van der Aa. pp. 8–9.
  23. ↑ ۲۳٫۰ ۲۳٫۱ ۲۳٫۲ Gibbs, P (1997). "How is the speed of light measured?". Usenet Physics FAQ. University of California, Riverside. Archived from the original on 2015-08-21. Retrieved 2010-01-13.
  24. ↑ Essen, L; Gordon-Smith, AC (1948). "The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator". Proceedings of the Royal Society of London A. 194 (1038): 348–61. Bibcode:1948RSPSA.194..348E. doi:10.1098/rspa.1948.0085. JSTOR 98293.
  25. ↑ Rosa, EB; Dorsey, NE (1907). "A new determination of the ratio of the electromagnetic to the electrostatic unit of electricity". Bulletin of the Bureau of Standards. 3 (6): 433. doi:10.6028/bulletin.070.
  26. ↑ Michelson, A. A. (1927). "Measurement of the Velocity of Light Between Mount Wilson and Mount San Antonio". The Astrophysical Journal. 65: 1. Bibcode:1927ApJ....65....1M. doi:10.1086/143021.
  27. ↑ Essen, L (1950). "The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator". Proceedings of the Royal Society of London A. 204 (1077): 260–77. Bibcode:1950RSPSA.204..260E. doi:10.1098/rspa.1950.0172. JSTOR 98433. S2CID 121261770.
  28. ↑ Froome, KD (1958). "A New Determination of the Free-Space Velocity of Electromagnetic Waves". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 247 (1248): 109–22. Bibcode:1958RSPSA.247..109F. doi:10.1098/rspa.1958.0172. JSTOR 100591. S2CID 121444888.
  29. ↑ Evenson, KM; et al. (1972). "Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser". Physical Review Letters. 29 (19): 1346–49. Bibcode:1972PhRvL..29.1346E. doi:10.1103/PhysRevLett.29.1346. S2CID 120300510.
  30. ↑ "Resolution 1 of the 17th CGPM". BIPM. 1983. Retrieved 2009-08-23.

یادداشت‌ها

[ویرایش]
  1. ↑ تا تاریخ ژانویه ۲۰۱۵
  2. ↑ اگرچه، بسامد نور با توجه به سرعت ناظر و منبع می‌تواند تغییر کند.

پیوند به بیرون

[ویرایش]
در ویکی‌انبار پرونده‌هایی دربارهٔ سرعت نور موجود است.

برگرفته از «https://fa.wikipedia.org/w/index.php?title=سرعت_نور&oldid=40573155»