فضا
| فیزیک نوین |
|---|

فَضا عبارت است از یک گستره سهبعدی نامحدود که اجسام در آن وجود و رویدادها در آن رخ میدهند و فاصله و جهت نسبی دارند.[۱] فضای فیزیکی اغلب در سه بُعد خطی تصور میشود، اما فیزیکدانان نوین معمولاً آن را در کنار زمان به عنوان یک پیوستار نامحدود ۴ بعدی به نام فضازمان توصیف میکنند. مفهوم فضا اهمیتی بنیادین در درک جهان فیزیکی دارد. اما بین فیلسوفان همچنان بر سر اینکه آیا فضا خود یک موجودیت است یا اینکه رابطهای میان موجودیتها یا بخشی از یک چارچوب مفهومی است، اختلاف نظر وجود دارد.
بحث در مورد ماهیت و حالت وجودی فضا به دوران باستان بازمیگردد مثلاً در رسالههایی چون تیمائوس افلاطون، یا سقراط در بازتابهایش از آنچه یونانیها khôra (به معنی فضا) میخواندند، یا در رساله فیزیک ارسطو (کتاب ۴، دلتا) در تعریف topos (به معنی مکان) یا بعدتر به عنوان مفهوم هندسی مکان در رساله «قول فی المکان» دانشمند سده یازده، ابن هیثم.[۲] بسیاری از پرسشهای کلاسیک فلسفی در رنسانس مورد بحث قرار گرفت و در قرن هفدهم و در زمان آغاز شکلگیری مکانیک کلاسیک مجدداً فرمولبندی شد. از دید ایزاک نیوتن، فضا مطلق بود، یعنی همیشگی بود و مستقل از اینکه مادهای در آن باشد یا نباشد.[۳] سایر فیلسوفان طبیعی از جمله گاتفرید لایبنیتز فکر میکردند که فضا مجموعهای از روابط میان اجسام بود که توسط فاصله و جهتشان نسبت به یکدیگر مشخص میشد. در قرن هجدهم یک فیلسوف و خداشناس به نام جرج بارکلی تلاش کرد تا قابلیت دیدن عمق فضایی را در مقالهاش با عنوان «به سوی نظریه جدیدتری برای دیدن» رد کند. امانوئل کانت متافیزیک دان چنین گفت که مفاهیم فضا و زمان، مفاهیم تجربی نیستند که از تجربیات دنیای خارج به دست آمدهباشند، بلکه اجزایی از یک چارچوب سیستماتیک هستند که در اختیار انسان قرار دارند و برای ساختار بخشیدن به همه تجربیات استفاده میشوند.
در سدههای ۱۹ام و ۲۰ام ریاضیدانان شروع به بررسی هندسههای نااقلیدسی نمودند که در آنها فضا به جای تخت بودن دارای انحناست. بنا بر نظریه نسبیت عام اینشتین، فضای اطراف میدانهای گرانشی از فضای اقلیدسی پیروی نمیکند[۴] آزمونهای نسبیت عام تأیید کردهاند که هندسههای نااقلیدسی مدل بهتری برای شکل فضا ارائه میکنند.
فلسفه فضا[ویرایش]
گالیلئو گالیله[ویرایش]
نظریههای گالیلهای و کارتزین دربارهٔ فضا، ماده و حرکت از بنیانهای انقلاب علمی هستند که با انتشار مبادی ریاضیات نیوتن در سال ۱۶۸۷به اوج رسید.[۵] نیوتن به کمک نظریههایش دربارهٔ فضا و زمان توانست حرکت اجسام را توضیح دهد. اگرچه نظریه وی به عنوان تاثیرگذارترین در فیزیک شناخته میشود، در واقع برآمده از ایدههای پیشینیان او در همان مورد بود.[۶]
گالیله به عنوان یکی از پیشگامان دانش نوین، ایدههای ارسطو و بطلمیوس درباره مرکزیت زمین در جهان بازبینی کرد. او با نظریه کوپرنیک موافق بود که خورشید مرکزی بود و در آن زمین و سایر سیارات به دور یک خورشید ثابت میگردند. اگر زمین حرکت میکند، باور ارسطویی مبنی بر اینکه گرایش طبیعی به سکون دارد، زیر سؤال میرود. گالیله میخواست به جای آن ثابت کند که خورشید دور محور خود میگردد؛ که حرکت هم دقیقاً به اندازه سکون، حالتی طبیعی برای یک جسم است. به عبارت دیگر برای گالیله، اجرام آسمانی از جمله زمین تمایل طبیعی به حرکت در مسیرهای دایرهای داشتند.[۷]
رنه دکارت[ویرایش]
دکارت میخواست جهانبینی ارسطویی را با نظریه ای درباره فضا و حرکت که توسط قوانین طبیعی تعیین میشوند، جایگزین کند. به عبارت دیگر او در جستجوی یک بنیان متافیزیکی یا توضیحی مکانیکی برای نظریههایش در مورد ماده و حرکت بود. فضای دکارتی ساختاری اقلیدسی دارد (نامتناهی، همگن و تخت)[۸]و به عنوان آنچه ماده را در برمیگیرد، تعریف میشود.[۵]
مفهوم دکارتی فضا، ارتباط تنگاتنگی با نظریههای او درباره ماهیت بدن، ذهن و ماده دارد. او بسیار به خاطر گفته معروفش؛ cogito ergo sum (من فکر میکنم پس هستم) و ایده اینکه تنها حقیقتی که میتوانیم به آن اطمینان داشته باشیم این است که شک میکنیم و در نتیجه فکر میکنیم، پس وجود داریم. نظریههای وی در مکتب خردگرایی جای میگیرند که دانش ما از جهان را به توانایی ما در تفکر نسبت میدهد؛ در مقابل تجربهگرایی که آن را به تجربیات نسبت میدهد[۹] او تمایز مشخصی بین ذهن و جسم قائل بود که به دوگانهانگاری دکارتی معروف است.
گافرید لایبنیتز و ایزاک نیوتن[ویرایش]

در قرن هفدهم فلسفه فضا و زمان به عنوان یک مسئله اساسی در اپیستمولوژی و متافیزیک ظهور کرد که در قلب آن گاتفرید لایبنیتز، فیلسوف و ریاضیدان آلمانی و ایزاک نیوتن، فیزیکدان و ریاضیدان انگلیسی قرار داشتند که دو نظریه مخالف در زمینه چیستی فضا ارائه دادند. لایبنیتز به جای آنکه فضا را موجودیت مستقلی بداند که در فرا و ورای ماده وجود دارد، بر این باور بود که فضا چیزی جز روابط فضایی میان اجسام در جهان نیست: «فضا یعنی چیزی که از در نظر گرفتن مکانها با هم نتیجه میشود»[۱۰] نواحی اشغال نشده، نواحی هستند که میتوانست جسمی در آنها قرار بگیرد و در نتیجه روابط فضایی با سایر مکانها داشته باشد؛ بنابراین برای لایبنیتز فضا یک انتزاع ایدئال از رابطه بین موجودیتها یا مکانهای آنها بود و در نتیجه نمیتوانست پیوسته باشد و میبایست گسسته باشد.[۱۱] فضا را میتوان شبیه به روابط بین اعضای خانواده تصور نمود. اگرچه افراد در خانواده با یکدیگر رابطه دارند، رابطهها مستقل از افراد وجود ندارند.[۱۲] لایبنیتز چنین استدلال کرد که فضا نمیتواند مستقل از اجسام در جهان وجود داشته باشد زیرا در این صورت دو جهان که دقیقاً یکسان باشند و تنها از نظر موقعیت دنیای مادی یکسان نباشند، از هم متفاوت خواهند بود. اما از آنجا که هیچ راه تجربی برای جدا کردن این دوجهان از یکدیگر وجود ندارد، بنا بر اصل هویت بازنشناختنیها هیچ تفاوت واقعی میان این دو جهان وجود ندارد. بر طبق اصل دلیل کافی هر نظریهای از فضا که از آن نتیجه شود که میتوان دو جهان متفاوت با چنین شرایطی داشت، نادرست است.[۱۳]

نیوتن باور داشت که فضا چیزی بیشتر از روابط میان اجسام مادی است و دیدگاهش را بر پایه مشاهده و آزمایش بنا نمود. یک نسبیتگرا نمیتواند تفاوتی بین حرکت لخت که در آن جسم با سرعت ثابت حرکت میکند و حرکت غیر لخت که در آن سرعت با زمان تغییر میکند، قائل شود زیرا همه اندازهگیریهای فضایی نسبت به اجسام دیگر و حرکتهای آنهاست. اما نیوتن استدلال نمود که چون حرکت غیر لخت نیرو ایجاد میکند، میبایست مطلق باشد[۱۴] او از مثال آب در یک سطل چرخان برای توضیح استدلالش استفاده نمود. آب در یک سطل آویزان از یک طناب نخست سطح صافی دارد و پس از شروع به چرخیدن سطل، سطح آب مقعر میشود. اگر سطل را از چرخش بازداریم سطح آب مقعر میماند زیرا به چرخش ادامه میدهد. در نتیجه مشخص است که سطح مقعر ناشی از حرکت نسبی میان سطل و آب نیست.[۱۵] بلکه طبق نظر نیوتن میبایست ناشی از حرکت غیر لخت نسبت به خود فضا بودهباشد. برای چندین قرن از استدلال سطل آب برای اینکه نشان داده شود که فضا مستقل از ماده وجود دارد، استفاده میشد.
امانوئل کانت[ویرایش]

در قرن هجدهم، فیلسوف آلمانی، امانوئل کانت نظریهای در مورد دانش ارائه داد که در آن دانش در مورد فضا میتواند هم پیشینی و هم ترکیبی باشد.[۱۶] بر طبق نظر کانت، دانش در مورد فضا ترکیبی است، زیرا گزارههایی که در مورد فضا بیان میشوند را نمیتوان صرفاً بر مبنای معانی کلمات در گزاره، درست دانست. در اثر خود کانت این دیدگاه که فضا یا باید ماده باشد یا رابطه را رد کرد. در عوض او به این نتیجه رسید که فضا و زمان توسط انسان کشف نشدهاند که ویژگیهای عینی دنیا باشند بلکه به عنوان بخشی از یک چارچوب که تجربه را سازماندهی میکند، توسط ما تحمیل میشوند.[۱۷]
هندسه نااقلیدسی[ویرایش]
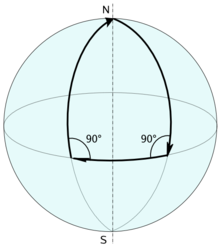
کتاب عناصر اقلیدس شامل پنج اصل است که زیربنای هندسه اقلیدسی را تشکیل میدهند. یکی از این اصول به نام اصل توازی موضوع بحث و اختلاف ریاضیدانان در سدههای متمادی بودهاست. این اصل چنین میگوید که در هر صفحهای که در آن یک خط راست L و یک نقطه P در خارج خط قرارگرفته باشد، تنها یک خط وجود دارد که از P میگذرد و با L موازی است. تا قرن نوزدهم عده کمی در درستی این اصل تردید داشتند و بحثها بیشتر حول این بود که آیا این یک اصل است یا اینکه یک نظریه است که میتوان آن را از اصول دیگر نتیجه گرفت.[۱۸] اما در حدود سال ۱۸۳۰، یانوش بوبویی مجارستانی ونیکلای لباچفسکی روس، بهطور جداگانه رسالههایی دربارهٔ نوعی از هندسه منتشر نمودند که شامل اصل توازی نبود و هندسه هذلولوی نام داشت. در این نوع از هندسه، بینهایت خط مختلف موازی میتوانست از P بگذرد. در نتیجه مجموع زاویهها در مثلث کمتر از ۱۸۰ درجه خواهد بود و و نسبت محیط دایره به قطر آن از عدد پی بزرگتر است. در دهه ۱۸۵۰، برنهارد ریمان نظریه معادلی برای هندسه بیضوی ارائه داد که در آن هیچ خط موازی از P نمیگذرد. در این نوع هندسه مجموع زوایای مثلث بیش از ۱۸۰ درجه و نسبت محیط دایره به قطر آن از عدد پی کوچکتر است.
| نوع هندسه | تعداد خطوط موازی | مجموع زوایا در مثلث | نسبت محیط به قطر دایره | اندازه خمش |
|---|---|---|---|---|
| هذلولوی | بینهایت | <۱۸۰° | > π | <۰ |
| اقلیدسی | ۱ | ۱۸۰° | π | ۰ |
| بیضوی | ۰ | > ۱۸۰° | <π | > ۰ |
کارل فریدریش گاوس و آنری پوانکاره[ویرایش]


اگرچه یک اجماع کانتی در آن زمان حاکم بود، وقتی هندسههای نااقلیدسی به رسمیت رسیدند برخی شروع به تأمل در مورد خمیدگی فضا نمودند. کارل فریدریش گاوس، یک ریاضیدان آلمانی نخستین کسی بود که به فکر یک بررسی تجربی در مورد ساختار هندسی فضا افتاد. او در این اندیشه بود که آزمونی برای بررسی مجموع زوایای یک مثلث ستارهای ترتیب دهد و گزارشهایی وجود دارد که او این کار را در مقیاسی کوچکتر با مثلثسازی قلههای کوهها در آلمان انجام داد.[۱۹]
آنری پوانکاره، یک ریاضیدان و فیزیکدان فرانسوی اواخر قرن نوزدهم، دیدگاه مهمی را معرفی نمود که طی آن سعی داشت بیثمر بودن هر گونه تلاش برای تعیین هندسه فضا از طریق آزمایش زا نمایش دهد.[۲۰] برای او اینکه چه هندسهای برای توصیف فضا به کار رود، یک مسئله قراردادی بود.[۲۱]
آلبرت اینشتین[ویرایش]

در سال ۱۹۰۵ آلبرت اینشتین نظریه نسبیت خاص را منتشر نمود که به این مفهوم منتهی میشد که فضا و زمان را میتوان به عنوان یک ساختار واحد به نام فضازمان در نظر گرفت. در این نظریه سرعت نور در خلاء برای تمام ناظرها یکسان است. از این موضوع میتوان نتیجه گرفت که اگر دو رویداد که از دید یک ناظر خاص همزمان هستند ممکن است برای ناظر دیگر همزمان نباشند. اگر ناظرها نسبت به هم در حرکت باشند ممکن است رویدادها از دید ناظر دیگر همزمان نباشند. علاوه بر این برای یک ناظر، ساعتی که نسبت به ناظر در حرکت است، کندتر از ساعتی که نسبت به او ساکن است، کار میکند؛ و اجسام در جهتی که نسبت به او حرکت میکنند، کوتاهتر میشوند.
در پی آن اینشتین روی نظریه نسبیت عام کار کرد که نظریهای در مورد نحوه برهمکنش گرانش با فضازمان است. به جای در نظر گرفتن گرانش به عنوان یک میدان نیرو که در فضازمان عمل میکند، اینشتین پیشنهاد داد که گرانش ساختار هندسی فضازمان را تغییر میدهد[۲۲] بر طبق نظریه عام او زمان در مکانهایی با پتانسیل گرانشی کمتر، آهستهتر میگذرد و پرتوهای نور در نزدیکی یک میدان گرانشی خمیده میشوند. دانشمندان با بررسی رفتار تپاخترهای دوتایی به تأیید پیشبینیهای اینشتین رسیدند و معمولاً برای توصیف فضازمان از هندسه نااقلیدسی استفاده میشود.
در فیزیک[ویرایش]
تعریف فضا در فیزیک مورد اختلاف است. مفاهیم گوناگونی که برای تعریف فضا استفاده شدهاند عبارتاند از:
- ساختاری که توسط یک مجموعه از «روابط فضایی» بین چیزها تعریف شدهاست.
- خمینهای (منیفلدی) که توسط یک دستگاه مختصاتی تعریف شده باشد که در آن بتوان مکان چیزها را تعیین کرد.
- نهادی که اشیاء موجود در جهان را از تماس و برخورد با یکدیگر بازمیدارد.
- وضعیتی در حوزهٔ معنایی وجود که «زمینه» ی اَشکال بروز یافته را فراهم میکند و بدین ترتیب حرکت و پویایی فیزیکی را ممکن میسازد.
در فیزیک کلاسیک، فضا، یک فضای اقلیدسی سهبعدی است که در آن هر موقعیتی را میتوان با استفاده از سه مختصات توصیف کرد. فیزیک نسبیت از فضا-زمان به جای فضا استفاده میکند، فضا-زمان به صورت یک خمینه چهاربعدی مدل میشود.
از جمله پرسشهای فلسفی دربارهٔ فضا عبارتاند از: آیا فضا مطلق است یا کاملاً نسبیتی است؟ آیا فضا هندسهٔ درست واحدی دارد یا اینکه هندسهٔ فضا فقط قرارداد است؟ از جمله شخصیتهای برجسته تاریخیای که در این مباحث موضع مشخصی داشتهاند، میتوان از آیزاک نیوتن (فضا مطلق است)، گوتفرید لایبنیتس (فضا نسبی است)، و هانری پوانکاره (هندسهٔ فضایی قراردادی است) نام برد.
تجربهٔهای ذهنی مرتبط با این پرسشها، بحث سطل نیوتن و جهان کروی پوانکاره هستند.
نگاه کنید به: مختصات کروی، مختصات دکارتی، فلسفه فیزیک
در معماری[ویرایش]
این مقاله نیازمند تمیزکاری است. لطفاً تا جای امکان آنرا از نظر املا، انشا، چیدمان و درستی بهتر کنید، سپس این برچسب را بردارید. محتویات این مقاله ممکن است غیر قابل اعتماد و نادرست یا جانبدارانه باشد یا قوانین حقوق پدیدآورندگان را نقض کرده باشد. |

با اینکه بسیاری از معماران، فضا را ذات و ماهیت معماری میدانند و با وجود مطالب زیادی که در باب اهمیت فضا در معماری عنوان شده و میشود، در فرهنگها و دانشنامهها تعریفی از مفهوم فضا در معماری به چشم نمیخورد. فقدان واژه فضا در کتابهای مرجع معماری نیز کاملاً قابل توجه و تعجبانگیز است.
دلیل این امر شاید این باشد که تلقی و کاربرد معماران از واژه فضا چنان واضح است که نیازی به توضیح واژهای کاملاً مشخص، احساس نمیکنند. اما این برهان ساده، آنجا که درمییابیم این واژه در متن تاریخ طولانی معماری نسبتاً جدید میباشد و در دهههای اخیر مفهومی بحثانگیز بودهاست، اعتبار خود را از دست میدهد.
با توجه به کمبود منابع جامع دربارهٔ فضای معماری و جدید بودن این مبحث، برای تبیین مفهوم فضا در تئوری معماری، بایستی به دیدگاههای معماران و نظریهپردازان در مورد مفهوم فضای معماری استناد نماییم. در میان نظریهپردازان معماری مدرن، برونو زوی و زیگفرید گیدئون از جمله افرادی هستند که به شکل نسبتاً جامعی مفهوم فضای معماری را مورد کنکاش قرار داده و سعی نمودهاند اهمیت آن را در معماری بازنمایانند.
برونو زوی معماری را هنر فضا و فضا را ذات معماری معرفی میکند، ولی او طبیعت فضای مورد بحث را مشخص نمینماید. برداشت او از فضا صورت واقعگرایانه دارد. به اعتقاد او، نماها و دیوارهای یک خانه، کلیسا یا کاخ مهم نیست که چقدر زیبا باشند، آنها تنها ظرفند و به جعبه شکل میدهند، نهاد و مظروف فضای داخلی است. ذات معماری برای زوی، سازماندهی معنادار فضا از طریق فرایند محدودسازی است؛ بنابراین از این دیدگاه، فضا مادهای با گسترش یکسان است که میتوان از طریق تعیین محدودهها در آن، به شیوههای مختلف به آن شکل داد.
برونو زوی با تعمیم مفهوم فضای معماری، فضای جدیدی با عنوان فضای شهری را نیز تعریف مینماید. او بر این عقیدهاست که تجربه فضایی معماری در شهر تداوم مییابد. در خیابانها، میدانها، کوچهها، پارکها، استادیومهای ورزشی، حیاط خانهها و در هر جایی که ساخته دست انسان خلاءها را محدود کرده و فضاهای بستهای به وجود آوردهاست. اگر در داخل بنایی فضا محدود به شش سطح باشد (کف، سقف و چهار دیوار)، بدین مفهوم نیست که خلاء بسته شده در پنج سطح (مانند یک حیاط یا یک میدان) به جای شش سطح، فضا بهشمار نمیآید. اما آیا میتوان حرکت در فضای بزرگراه خط مستقیم و یکنواختی را که کیلومترها در دشتی غیرمسکونی پیش رفتهاست، به عنوان یک تجربه فضایی مطرح ساخت؟ مسلم است آنچه در جهت دید بهوسیله یک سطح چه از طریق دیوارسازی یا از طریق کاشتن درخت یا بهوسیله عناصری که فضاهای معماری را متمایز میکنند، محدود شده باشد، فضای شهری محسوب میشود. زوی با استناد به توضیحات فوق، چنین نتیجهگیری میکند که هر بنا همزمان دو فضا را به وجود میآورد: فضای داخلی که بهوسیله اثر معماری معین شدهاست و فضای خارجی یا شهری که بهوسیله آن اثر معماری و آثار نزدیک به آن ایجاد شدهاست.
مفهومی که برونو زوی از فضای معماری مطرح مینماید، هنوز پذیرش عام دارد و مورد استناد بسیاری از نظریهپردازان میباشد. برای نمونه به گفته وان درلان، فضای معماری با برافراشتن دو دیوار پا به عرصه وجود مینهد، دو دیوار فضایی جدید میان خود پدیدمیآورند که از فضای طبیعی پیرامون آنها مجزا میشود.
در واژهنامه تخصصی معماری واژه فضا در حوزه معماری و هنرهای دیداری این گونه تعریف شدهاست:
فضا: حوزههای گسترش یابنده و در عین حال فراگیرنده بوده و جایگاه یا محیطی را در ابعاد جسمانی یا فیزیکی و روانشناختی تعریف مینماید. از کل روابط شکل، رنگ و حرکت شکل گرفته، گاه خالی یا منفی است و گاه فاصله میان عناصر را مشخص مینماید، خواه این فاصله در سطح باشد یا در عمق که توسط قواعد پرسپکتیو مجسم میشود. فضای دو بعدی فقط طول و عرض داشته، فضای تزئینی نیز به طول و عرض محدود میباشد.[۲۳]
۱. (۲) اجزاء و مثل اتاقها و تالار و حیاط، جای تهی، حجم پر نشده و توخالی، کیفیت و بیان معماری.
فضای سه بعدی[ویرایش]
فضای سه بعدی شامل عمق، طول و عرض است. فضای چهار بعدی، علاوه بر ابعاد سهگانه بعد زمان را میرساند که به آن، فضای لایتناهی میگویند. تصویری است که توهم فضا در آن معادل بی بیکرانگی در محیط است.
فضای کنترل شدهٔ ساختمان[ویرایش]
بخشهایی از فضای داخلی ساختمان که مورد کاربرد انسانها قرار میگیرد و در طول اوقات سرد سال، گرم شده و طی اوقات گرم سال، خنک میشود. شرایط دمای این فضاها در ساختمان باید در محدودهٔ آسایش باشد.
فضای کنترل نشدهٔ ساختمان[ویرایش]
بخشهایی از فضای درونی ساختمان که در اوقات گرم یا سرد سال ضروری نیست خنک یا سرد شوند. م. انبارها، پارکینگهایی که از سه طرف با دیوار محصورند، دالانها و مانند آنها.
فضای معماری[ویرایش]
فضای معماری، فضایی که توسط سطوح، به شکلهای گوناگون محدود گشته و به عملکردهای تعیین شده پاسخ میگوید که موضوع و جوهر اصلی معماری است.
معماری عبارت است از علم و هنر شکل بخش فضای زیست انسان، به عبارت دیگر معماری به وجود آورندهٔ فضایی است که انسان را از عوامل طبیعی مصون داشته و فعالیت زندگی فردی و اجتماعی او را دربرگرفته و به نیازهای مادی و معنوی انسان پاسخگو خواهد بود.
پس میتوان گفت، فضایی که توسط سطوح عمودی و افقی به وجود میآید، موضوع و جوهر اصلی معماریست به عبارت دیگر موضوع اصلی و در حقیقت جوهر معماری، فضا است. یک ساختمان، فقط مجموعهای از طول، عرض و عمق نیست بلکه مجموعهای است از اندازههای مختلف فضاهای خالی که انسان میتواند در آن حرکت و زندگی کند.[۲۴]
در ستارهشناسی[ویرایش]
فضا قسمتهای نسبتاً تهی کیهان است که بیرون از جوّ سیارات قرار دارد. فضا را گاهی برای تمایز از فضای جوّ و مکانهای زمینی، «فضای میان ستارهای» مینامند.
از آنجا که جوّ زمین ناگهان تمام نمیشود، بلکه کمکم با افزایش ارتفاع رقیق میشود، مرز مشخصی میان فضا و جوّ وجود ندارد. در ایالات متحده آمریکا، به افرادی که بالاتر از بلندای ۵۰ مایلی (۸۰ کیلومتری) سفر کنند، فضانورد گفته میشود. ارتفاع ۴۰۰٬۰۰۰ پایی (۱۲۰ کیلومتری) مرزی است که آثار جوّی در ورود دوباره مشهود میشوند. غالباً از ارتفاع ۱۰۰ کیلومتری به عنوان مرز میان جوّ و فضا یاد میشود.
نگاه کنید به: فیزیک نجومی، هوافضا، فناوری فضایی، مهاجرت به فضا، شاتل فضایی، فضا-زمان
در ریاضیات[ویرایش]
در ریاضیات، فضا مجموعهای است که معمولاً ساختار اضافیای هم دارد.
برای نمونه، نگاه کنید به فضای اقلیدسی، فضای برداری، فضای برداری هنجارین، فضای باناخ، فضای ضرب داخلی، فضای هیلبرت، فضای توپولوژیک، فضای یکنواخت، فضای متریک.
در روانشناسی[ویرایش]
اصطلاح فضای درون گاهی برای توصیف محتویات ذهن انسان به کار برده شدهاست.
فضای تاریخی[ویرایش]
ممکن است شیئی متعلق به گذشتههای دور باشد. چقدر دور؟ این سؤال یک معنای عام و یک معنای خاص دارد. برای خیلی از افراد ده هزار سال قبل با بیست هزار سال قبل تفاوتی نمیکند. حتی برای بعضیها صدسال قبل با پنجاه سال قبل هم فرق نمیکند. درحالیکه برای باستانشناس، مورخ، دانشمند یا هرکس که علاقهمند به دورههای تاریخی باشد، بسیار متفاوت است.
چگونه میشود این دورهها را احساس کرد و از هم تمیز داد؟ آشنا شدن با آثار به جا مانده از دورهها در همهٔ زمینههای معماری، ادبیات، هنر، لباس و … میتواند این احساس را ایجاد یا تقویت کند. گاهی برای ما دورهٔ خاصی از تاریخ اهمیت ندارد اما یک احساس عمومی و کلی از گذشته ما را در یک فضای تاریخی قرار میدهد. برای اینکار باید اشیاء و آثار اصلی را دید.
به یاد داشته باشیم که اشیای گذشته متعلق به زمانی هستند که در یک مجموعهٔ زنده و پویا مورد استفاده قرار میگرفتند. حتی کلمات و ادبیات و محاورات در زمان خودش بیشترین زندگی و حیات را داشتهاست، اما به تدریج جان باخته و جسمی از آن به یادگار ماندهاست، لذا به هر میزان که بتوانیم خود را در شرایط و زندگی همزمان این آثار قرار دهیم. گویی که تقریباً حیات فرهنگی و تمدنی آن روزگار را احساس کردهایم و خود را اگرچه با فاصلهٔ زیاد یکی از افراد آن روزگار میپنداریم در این صورت به فضای تاریخ وارد شدهایم. میتوان گفت هرچه ما نسبت زمانی خود را با اثر گذشته کم کرده و به آن زمان نزدیک شویم، وارد فضای تاریخ و هرقدر خود را از شیء یا اثر گذشته دور بدانیم با دیدن یا قرار گرفتن در یک یا مجموعهای از آنها به فضای تاریخی نزدیک شدهایم. گاهی اوقات آثار گذشتگان به دلایل عام یا خاص با ما ارتباط بیشتری پیدا میکنند؛ مثلاً بعضی از این آثار امروز هم مورد استفاده قرار میگیرند. اگرچه با تغییر در کاربری آن مثل فرش و… این باعث پیوند ما به گذشته و احساس مشترک با آنها میشود. هرچه این تعلق به آثار بیشتر باشد، این پیوند قویتر است.
پیوند به بیرون[ویرایش]
- سازمان فضایی ایران بایگانیشده در ۳۰ سپتامبر ۲۰۰۷ توسط Wayback Machine
منابع[ویرایش]
- ↑ "space - physics and metaphysics". Encyclopedia Britannica.
- ↑ Refer to Plato's Timaeus in the Loeb Classical Library, Harvard University, and to his reflections on khora. See also Aristotle's Physics, Book IV, Chapter 5, on the definition of topos. Concerning Ibn al-Haytham's 11th century conception of "geometrical place" as "spatial extension", which is akin to Descartes' and Leibniz's 17th century notions of extensio and analysis situs, and his own mathematical refutation of Aristotle's definition of topos in natural philosophy, refer to: Nader El-Bizri, "In Defence of the Sovereignty of Philosophy: al-Baghdadi's Critique of Ibn al-Haytham's Geometrisation of Place", Arabic Sciences and Philosophy (Cambridge University Press), Vol. 17 (2007), pp. 57-80.
- ↑ French and Ebison, Classical Mechanics, p. 1
- ↑ Carnap, R. An introduction to the Philosophy of Science
- ↑ ۵٫۰ ۵٫۱ Space from Zeno to Einstein: classic readings with a contemporary commentary. Huggett, Nick. Cambridge, Mass.: MIT Press. 1999. Bibcode:1999sze..book.....H. ISBN 978-0-585-05570-1. OCLC 42855123.
{{cite book}}: نگهداری CS1: سایر موارد (link) - ↑ Janiak, Andrew (2015). "Space and Motion in Nature and Scripture: Galileo, Descartes, Newton". Studies in History and Philosophy of Science. 51: 89–99. doi:10.1016/j.shpsa.2015.02.004. PMID 26227236.
- ↑ 1958–, Dainton, Barry (2001). Time and space. Montreal: McGill-Queen's University Press. ISBN 978-0-7735-2302-9. OCLC 47691120.
{{cite book}}: CS1 maint: numeric names: فهرست نویسندگان (link) - ↑ Dainton, Barry (2014). Time and Space. McGill-Queen's University Press. p. 164.
- ↑ Tom., Sorell (2000). Descartes: a very short introduction. Oxford: Oxford University Press. ISBN 978-0-19-154036-3. OCLC 428970574.
- ↑ Leibniz, Fifth letter to Samuel Clarke
- ↑ Vailati, E, Leibniz & Clarke: A Study of Their Correspondence p. 115
- ↑ Sklar, L, Philosophy of Physics, p. 20
- ↑ Sklar, L, Philosophy of Physics, p. 21
- ↑ Sklar, L, Philosophy of Physics, p. 22
- ↑ «Newton's bucket». www-groups.dcs.st-and.ac.uk. دریافتشده در ۲۰۱۶-۱۲-۱۱.
- ↑ Carnap, R, An introduction to the philosophy of science, p. 177-178
- ↑ Lucas, John Randolph. Space, Time and Causality. p. 149. ISBN 0-19-875057-9.
- ↑ Carnap, R, An introduction to the philosophy of science, p. 126
- ↑ Carnap, R, An introduction to the philosophy of science, p. 134-136
- ↑ Jammer, M, Concepts of Space, p. 165
- ↑ Carnap, R, An introduction to the philosophy of science, p. 148
- ↑ Sklar, L, Philosophy of Physics, p. 43
- ↑ (سید صدر، ۱۳۸۰: ۴۱۲)
- ↑ سید صدر، ۱۳۸۰: ۴۱۲
- Reichenbach, Hans. The Philosophy of Space & Time, Translated by Maria Reichenbach and John Freuned, Dover Publications, Inc. , New York, 1957. Standard Book Number: ۴۸۶-۶۰۴۴۳-۸
- صدر، سید ابوالقاسم. (۱۳۸۰). دائرةالمعارف معماری و شهرسازی (مصور). ویرایش محسن نیکبخت، تهران: انتشارات آزاده.

در ویکیانبار پروندههایی دربارهٔ فضا موجود است.



