ریاضیات
 | ||
| ریاضیات | ||
|---|---|---|
|
|
||
| ناوبری | ||


ریاضیدان یونانی سده سوم قبل از میلاد
این حد از جزئیات بر اساس تصور رافائل از مکتب آتن است.
ریاضیات (به پارسی سره: انگارش یا رایش)[۱] (به تاجیکی: مَتِماتیک) (به انگلیسی: mathematics) فن محاسبهٔ اعداد بوده و نیز به مطالعهٔ مباحثی چون کمیت (نظریه اعداد)،[۲] ساختار (جبر)،[۳] فضا (هندسه)،[۲] و تغییرات (آنالیز ریاضیات)[۴] میپردازد.[۵][۶][۷] در حقیقت، تعریفی جهانی که همه بر سر آن توافق داشته باشند، برای ریاضیات وجود ندارد.
ریاضیدانان به دنبال الگوهایی هستند که بتوان از آنها استفاده کرده و حدسهای جدید را بهصورت فرمول درآورد؛ آنها درستی یا نادرستی حدسها را با اثبات ریاضی نشان میدهند. هرگاه ساختارهای ریاضی مدلهای خوبی از پدیدههای جهان واقعی باشند، استدلال ریاضی میتواند پیشبینیهایی برای طبیعت ارائه کند. علم ریاضیات با استفاده از انتزاع و منطق از مفاهیمی چون شمردن، محاسبه و اندازهگیری و مطالعهٔ نظاممند شکلها و حرکات اشیای فیزیکی بهوجود آمد. ریاضیات کاربردی از زمانی که انسان نوشتن را آموخت، بهعنوان فعالیتی بشری وجود داشتهاست. تحقیقات مورد نیاز برای حل مسائل ریاضی، ممکن است سالها یا حتی سدهها طول بکشد.
استدلالهای استوار ابتدا در ریاضیات یونان باستان ظاهر شدند؛ بهخصوص در اثر عناصر اقلیدس. از زمان کارهای تحقیقاتی جوزپه پئانو (۱۸۵۸–۱۹۳۲)، داویت هیلبرت (۱۸۶۲–۱۹۴۳) و دیگران بر روی دستگاه اصول موضوعهای در پایان سده نوزدهم میلادی، روش تحقیقاتی ریاضیدانان به این شکل درآمده که آنها حقایق را با استدلال ریاضی از مجموعهٔ منتخبی از اصول موضوعی و تعاریف به دست میآورند. روند پیشرفت ریاضیات تا زمان رنسانس سرعت نسبتاً آرامی داشت، تا زمانی که نوآوریهای ریاضیاتی با کشفیات علمی برهمکنش کرده و منجر به افزایش سریع نرخ اکتشافات ریاضی گشت و تا به امروز نیز ادامه دارد.[۸]
ریاضیات در بسیاری از زمینهها مثل علوم طبیعی، مهندسی، پزشکی، اقتصاد و علوم اجتماعی یک علم ضروری است. شاخههای کاملاً جدیدی در ریاضیات بهوجود آمدهاند؛ مثل نظریهٔ بازیها. ریاضیدانان در ریاضیات محض (مطالعهٔ ریاضی به هدف کشف هرچه بیشتر رازهای خود آن) بدون اینکه هیچگونه هدف کاربردی در ذهن داشته باشند به تحقیقات میپردازند؛ در حالی که کاربردهای عملی یافتههای آنها معمولاً بعدها کشف میشود.[۹] مادر علوم جهان ریاضیات است.
تاریخچه[ویرایش]


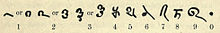
تاریخ ریاضیات را میتوان به عنوان دنبالهای از تجریدسازیهای فزاینده دید. اولین قابلیت تجریدسازی که در بسیاری از حیوانات مشترک است،[۱۰] احتمالاً مفهوم عدد است؛ فهم این مطلب که مجموعهٔ دو سیب و مجموعهٔ دو پرتقال (بهعنوان مثال) با هم اشتراکی دارند، و آن کمیت تعدادشان است.
همانطور که شواهد بر روی چوبخط نشان میدهد، مردم پیشاتاریخ میتوانستند اشیاء فیزیکی را بشمرند و توانایی شمردن اشیاء تجریدی مثل روز، فصل و سال را نیز داشتند.[۱۱][۱۲]
شواهد مربوط به ریاضیات پیچیدهتر تا ۳۰۰۰ قبل میلاد مشاهده نشده، زمانی که بابلیها و مصریها شروع به استفاده از حساب، جبر و هندسه برای محاسبات مربوط به مالیات و دیگر مفاهیم اقتصادی، و ساخت و ساز یا نجوم کردند.[۱۳] قدیمیترین متون ریاضیاتی مربوط به بینالنهرین و مصر میشود که به ۲۰۰۰–۱۸۰۰ قبل از میلاد بازمیگردد. بسیاری از متون اولیه سه تاییهای فیثاغوری را ذکر کرده و لذا به نظر میرسد که قضیه فیثاغورس کهنترین و گستردهترین توسعه ریاضیاتی بعد از حساب مقدماتی و هندسه باشد. در اسناد تاریخی، در ریاضیات بابلیها بود که حساب مقدماتی (جمع، تفریق، ضرب و تقسیم) ابتدا پدیدار گشت. بابلیها همچنین از یک دستگاه مکان-ارزشی بهره میجستند که در آن دستگاه اعداد پایه ۶۰ پیادهسازی شده بود، ازین دستگاه عددی هنوز هم برای اندازهگیری زاویه و زمان استفاده میشود.[۱۴]
با آغاز سده ششم قبل از میلاد مسیح، ریاضیات یونانیها با فیثاغورسیها مطالعهٔ نظام مندی را در ریاضیات، به هدف شناخت بیشتر خود ریاضیات آغاز نمودند که سرآغاز ریاضیات یونانیها بود.[۱۵] حدود ۳۰۰ قبل از میلاد، اقلیدس روش اصول موضوعه ای را که هنوز هم در ریاضیات به کار میرود را معرفی کرد که شامل تعاریف، اصول، قضیه و اثبات بود. کتاب مرجع او که به اصول اقلیدس معروف است بهطور گسترده به عنوان موفقترین و تأثیر گذارترین کتاب مرجع همه زمانها شناخته میشود.[۱۶] بزرگترین ریاضیدانان باستان را اغلب ارشمیدس (۲۸۷ تا ۲۱۲ قبل از میلاد) اهل سیراکوز میدانند.[۱۷] او فرمولهایی برای محاسبهٔ مساحت و حجم اجسام در حال دوران پیدا کرد و از روش افنا برای محاسبه مساحت زیر منحنی سهمی با استفاده از جمع یک سری بینهایت استفاده کرد به گونه ای که بی شباهت با حساب دیفرانسیل و انتگرال مدرن نیست.[۱۸] دیگر دستاوردهای قابل توجه در ریاضیات یونان مقاطع مخروطی (آپولونیوس اهل پرگا، سده سوم قبل از میلاد)،[۱۹] مثلثات (هیپارکوس اهل نیکا (سده دوم قبل از میلاد))،[۲۰] و آغاز جبر (دیوفانتوس، سده سوم پس از میلاد) بود.[۲۱]
سیستم عددی هندو-عربی و قواعد استفاده از عملیاتش که امروزه در سراسر جهان استفاده میشود، در طی هزارهٔ اول میلادی در هند توسعه یافت و سپس از طریق ریاضیات اسلامی به جهان غرب انتقال یافت. دیگر پیشرفتهای مربوط به ریاضیات هندیها شامل تعریف مدرن سینوس و کسینوس و فرم اولیه سریهای بینهایتی است.

در طی عصر طلایی اسلام، که در سده نهم و دهم میلادی شکل گرفت، ریاضیات نوآوریهای مهمی را به خود دید که بر اساس ریاضیات یونانیها پایهریزی شده بود. مهمترین دستاوردهای ریاضیات اسلامی توسعهٔ جبر بود. دیگر دستاوردهای مهم ریاضیات دورهٔ اسلامی پیشرفت در مثلثات کروی و اضافه شدن اعشار به سیستم عددی عربی بود. بسیاری از ریاضیدانان این دوره فارسیزبان بودند مثل خوارزمی، خیام و شرف الدین توسی.
در طی اوایل عصر مدرن، ریاضیات شروع به توسعه شتاب داری در غرب اروپا کرد. توسعه حساب دیفرانسیل و انتگرال توسط نیوتون و لایبنیتس در سده هفدهم میلادی ریاضیات را متحول کرد. لئونارد اویلر مهمترین ریاضیدان سده هجدهم میلادی بود که چندین قضیه و کشفیات را به ریاضیات افزود. شاید مهمترین ریاضیدانان سده نوزدهم میلادی ریاضیدان آلمانی کارل فردریش گاوس بود که خدمات متعددی به شاخههای مختلف ریاضیات چون جبر، آنالیز، هندسه دیفرانسیل، نظریه ماتریس، نظریه اعداد و آمار کرد. در اوایل سده بیستم میلادی، کورت گودل، ریاضیات را با انتشار قضایای ناتمامیت خویش دچار تغییر کرد. این قضایا نشان دادند که هر سیستم اصول موضوعه سازگاری شامل گزارههای غیرقابل اثبات اند.
ریاضیات از آن زمان بهطور گستردهای توسعه یافتهاست و کنش و واکنشهای ثمربخشی بین ریاضیات و علوم ایجاد شده که به نفع هردو است. کشفیات ریاضیات تا به امروز نیز ادامه دارد. بر اساس نظر میخائیل سوریوک، که در ژانویه ۲۰۰۶ در بولتن انجمن ریاضی آمریکا منتشر شد، "تعداد مقالات و کتب پایگاه اطلاعاتی ژورنال Mathematical Review از سال ۱۹۴۰ (اولین سال عملیاتی شدن MR) اکنون به ۱٫۹ میلیون میرسد که سالانه بیش از ۷۵ هزار مورد به این پایگاه افزوده میشود. اکثریت کارهای گستردهای که در این اقیانوس وجود دارد شامل قضایای جدید ریاضیاتی و اثباتهایشان است.
شاخههای ریاضیات[ویرایش]

ریاضیات را میتوان بهطور خیلی کلی به چند قسمت تقسیم کرد: مطالعه کمیت، ساختار، فضا و تغییرات (یعنی حساب، جبر، هندسه و آنالیز). علاوه بر اینها که دغدغههای اصلی ریاضیات هستند، گرایشهای دیگری نیز وجود دارند که خود را وقف کاوش ارتباطات بین قلب ریاضیات با دیگر زمینههای ریاضیات کردهاند، مثل ارتباطش با منطق، نظریه مجموعهها (شالودههای ریاضی)، یا دیگر شاخههای تجربی تر ریاضیات که در علوم مختلف کاربرد دارند (ریاضیات کاربردی)، و اخیراً مطالعه عدم قطعیت. در حالی که برخی از این قلمروها ممکن است به ظاهر غیر مرتبط به نظر برسند، برنامه لنگلندز ارتباطاتی بین شاخههایی را یافتهاست که پیش از این غیر مرتبط تلقی میشدند، مثل گروههای گالوا، رویههای ریمانی و نظریه اعداد.
بنیان ریاضیات و فلسفه[ویرایش]
نظریه مجموعهها و منطق ریاضی به منظور تببین بنیانهای ریاضیات توسعه یافتهاند. منطق ریاضی شامل مطالعهٔ منطق و کاربردهای منطق صوری به شاخههایی از ریاضیات است؛ نظریه مجموعهها شاخه ای از ریاضیات است که به مطالعه مجموعهها یا گردایه ای از اشیاء میپردازد. نظریه رستهها که به صورت مجرد به مطالعه ساختارهای ریاضیاتی و ارتباطشان با هم میپردازد هنوز هم در حال تکوین است. عبارت «بحران بنیانهای ریاضیاتی» به دوره ای تاریخی بین ۱۹۰۰ تا ۱۹۳۰ اشاره دارد که در آن دوره جستجویی برای یافتن بنیانی مستحکم برای ریاضیات انجام شد.[۲۲] اختلاف نظرها در مورد بنیانهای ریاضی تا زمان کنونی هم ادامه دارد. این بحران با یک سری بحثها تحریک شد، از جمله این بحثها، بحث بر سر نظریه مجموعههای کانتور و جدال هیلبرت-براور بود.
دغدغهٔ منطق ریاضیاتی، ایجاد چارچوب مستحکم اصول موضوعه ای برای ریاضیات است. منطق ریاضی الزامات چنین چارچوبی را مطالعه میکند. بهطور مثال قضایای عدم کمال گودل بهطور ضمنی میگویند که هر نظام صوری اگر معنا دار باشد (یعنی تمام قضیههایی که میتوان آنها را اثبات کرد درست باشند)، الزاماً ناکامل اند (یعنی قضایای درستی هستند که نمیتوان آنها را در این سیستم اثبات کرد). گودل نشان داد که هر گردایه متناهی از اصول موضوعههای نظریه اعداد را به عنوان اصول موضوعه در نظر بگیریم، میتوان یک جمله صوری ساخت که از نظر حقایق نظریه اعداد صحیح باشد ولی از این اصول موضوعه بهدست نیایند؛ لذا در نظریه اعداد هیچ نظام صوری که از نظر اصول موضوعه ای کامل باشد وجود ندارد. منطق نوین به چند بخش تقسیم میشود: نظریه بازگشت، نظریه مدل و نظریه اثبات و ارتباط نزدیکی با علوم رایانه و نظریه رستهها دارد. در زمینهٔ نظریه بازگشت، عدم امکان وجود سیستم اصول موضوعه ای کامل را میتوان به صورت صوری از طریق پیامدهای قضیه MRDP نشان داد.
علوم رایانه شامل نظریه محاسبه پذیری، نظریه پیچیدگی محاسباتی و نظریه اطلاعات است. نظریه رایانشپذیری محدودیتهای مدلهای مختلف نظری رایانهها را بررسی میکند که شامل بسیاری از مدلهای شناخته شده چون ماشین تورینگ میشود. نظریه پیچیدگی به مطالعهٔ رام پذیری حل مسائل در رایانه میپردازد. برخی مسائل وجود دارند که با وجود این که از لحاظ نظری توسط رایانه قابل حل هستند، اما در عمل هزینه حل کردنشان از نظر زمان یا فضا زیاد است و عملاً با وجود پیشرفتهای سریع سختافزاری در دنیای رایانه حل آنها به نظر نامعقول میآید. یک مسئله مشهور در این وادی مسئلهٔ "P=NP"؟ است که برای حل آن جایزهٔ مسائل هزاره تعیین شدهاست.[۲۳] در نهایت، نظریه اطلاعات با حجمی از دادهها سر و کار دارد که بتوان آنها را بر روی یک وسیله خاص ذخیره کرد، پس این علم با مفاهیمی چون فشرده سازی و انتروپی سروکار دارد.
ریاضی محض[ویرایش]
کمیت[ویرایش]
مطالعهٔ کمیت با اعداد آغاز میگردد، ابتدا مطالعهٔ اعداد طبیعی و اعداد صحیح و عملیات حسابی روی آنها که در شاخه حساب انجام میگردد. خواص عمیقتر اعداد در نظریه اعداد صورت میپذیرد، که قضایای معروفی چون آخرین قضیه فرما از آن بیرون میآید. اعداد اول دوقلو و حدس گلدباخ دو تا از مسائل لاینحل نظریه اعدادند.
با پیشرفت دستگاه اعداد، اعداد صحیح به عنوان زیر مجموعهای از اعداد گویا («کسرها») شناخته شدند. خود اعداد گویا زیر مجموعهٔ اعداد حقیقی میباشند که از آنها برای نمایش مفهوم کمیتهای پیوسته استفاده شدهاست. خود اعداد حقیقی زیر مجموعهٔ اعداد مختلط اند. اینها اولین قدمها در سلسله مراتب اعداد است که شامل چهارگانها و هشتگانها باشد. با در نظر گرفتن اعداد طبیعی، میتوان به اعداد ترامتناهی رسید که مفهوم «بی نهایت» بودن را صوری میکنند. بر اساس قضیه بنیادی جبر، تمام جوابهای چند جملهایهای تک متغیره با ضرایب مختلط، صرف نظر از درجهشان مختلط هستند. یکی دیگر از قلمروهای مطالعاتی مربوط به اندازه مجموعهها میشود، که در اعداد کاردینال توصیف گشتهاند. مثل اعداد الف که امکان مقایسهٔ مجموعههای نامتناهی را با هم میدهند.
ساختار[ویرایش]
بسیاری از اشیاء ریاضیاتی، مثل مجموعه اعداد و توابع، ساختار داخلی از خود بروز میدهند که میتواند پیامد عملیات یا روابطی باشند که بر روی یک مجموعه اعمال میشود. سپس ریاضیات به مطالعه خواص آن مجموعههایی میپردازد که میتوان آنها را بر اساس آن ساختار مورد نظر بیان کرد؛ به عنوان مثال نظریه اعداد به مطالعه خواص مجموعه اعداد صحیح میپردازد که میتوان آنها را با عملیات حساب بهدستآورد. به علاوه، معمولاً اتفاقی که میافتد این است که چنین مجموعههای ساخت یافته (ساختارها) خواص مشابهی از خود بروز میدهند که امکان انجام یک مرحله تجرید دیگر بر روی آنها را داده و لذا در چنین شرایطی میتوان اصول موضعههایی برای آن دسته خاص از مجموعهها ارائه داد، و سپس به مطالعهٔ همه آنها به صورت یکجا پرداخت (همه آن مجموعههایی که در آن اصول موضوعه صدق میکنند). ازین رو، میتوان گروهها، حلقهها، میدانها و دیگر نظامهای مجرد را مطالعه کرد؛ چنین مطالعاتی (برای ساختارهای تعریف شده با عملیات جبری) تشکیل یک قلمرو از ریاضیات به نام جبر مجرد را میدهند.
جبر مجرد را میتوان در حالت کلی آن به مسائل به ظاهر غیر مرتبط اعمال کرد؛ به عنوان مثال، تعدادی از مسائل مربوط به ساخت به کمک خطکش و پرگار در نهایت با کمک نظریه گالوا حل شدند، که در آن از نظریه میدان و گروهها استفاده شد. یکی دیگر از مثالهای مرتبط با نظریه جبری، جبر خطیست، که عناصر آن بردارها میباشند. بردارها هم اندازه دارند و هم جهت و میتوان از آنها برای مدلسازی روابط بین نقاط درون فضا استفاده کرد. این مثالی از پدیده ای است که پیشتر اشاره شد، یعنی ارتباط قلمروهای به ظاهر غیر مرتبط مثل هندسه و جبر، به گونه ای که مشخص میشود این قلمروهای به ظاهر غیر مرتبط ارتباطاتی بس عمیقتر با یک دیگر در ریاضیات مدرن دارند. ترکیبیات به مطالعه راههای شمارش تعدادی اشیاء میپردازد که آن اشیاء در ساختار داده شدهای صدق میکنند.
فضا[ویرایش]
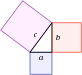
مطالعه فضا از هندسه آغاز شد، بهخصوص هندسه اقلیدسی که فضا و اعداد را با هم ترکیب کرده و قضیه معروف فیثاغورس را بهوجود آورد. مثلثات شاخه ای از ریاضیات است که درگیر ارتباطات بین اضلاع و زاویههای مثلث و توابع مثلثاتی است. در مطالعات مدرن فضا، این ایدهها تعمیم یافته تا به هندسههایی با ابعاد بالاتر، فضاهای غیر-اقلیدسی (که نقش بنیادینی در نسبیت عام دارند) و توپولوژی برسد. کمیت و فضا هردو نقش بنیادینی در هندسه تحلیلی، هندسه دیفرانسیل و هندسه جبری دارند. هندسه محدب و گسسته برای حل مسائلی در نظریه اعداد و آنالیز تابعی توسعه یافتند، اما اکنون به نیت کاربردهایشان در بهینهسازی و علوم رایانه دنبال میشوند. در هندسه دیفرانسیل مفاهیم کلافهای تاری و حساب دیفرانسیل و انتگرال بر روی منیفلدها، بهخصوص بردارها و حساب تانسوری وجود دارد. در هندسه جبری توصیف اشیاء هندسی مربوط به مجموعه جواب چند جمله ایها بحث میشود که مفاهیم کمیت و فضا را با هم ترکیب میکند. همچنین در مطالعه بر روی گروههای توپولوژی نیز به دنبال ترکیب ساختار و فضاییم. گروههای لی در مطالعه فضا، ساختار و تغییرات استفاده میشود. توپولوژی در تمام شاخههای متعدد خویش را میتوان به عنوان بزرگترین رشد در ریاضیات سده بیستم تلقی کرد. شاخههای توپولوژی شامل توپولوژی نقطه ای، توپولوژی نظریه مجموعه ای، توپولوژی جبری و توپولوژی دیفرانسیل است. به عنوان مثال توپولوژی عصر جدید شامل قضیهٔ مترپذیری، نظریه اصول موضوعه ای مجموعهها، نظریه هوموتوپی و نظریه مورس است. توپولوژی همچنین اکنون شامل حدس اثبات شدهٔ پوانکاره بوده و هنوز قلمروهای لاینحلی چون حدس هاج را دربردارد. دیگر نتایج هندسه و توپولوژی شامل قضیه چهار رنگ و حدس کپلر است که به کمک رایانهها اثبات شدهاند.
تغییر[ویرایش]
فهم و توصیف تغییر تم اصلی علوم طبیعی بوده و حساب دیفرانسیل و انتگرال به عنوان ابزاری برای تحقیق در این ارتباط ساخته شد. توابع در اینجا به عنوان مفهوم مرکزی توصیف کننده یک کمیت متغیر ظهور پیدا کردند. مطالعه مستحکم اعداد حقیقی و توابع تک متغیرهٔ حقیقی را آنالیز حقیقی گویند، آنالیز مختلط هم فیلد مشابهی است که بر روی میدان اعداد مختلط کار میکند. آنالیز تابعی بر روی فضاهای (اغلب بینهایت بعدی) توابع متمرکز است. یکی از کاربردهای متعدد آنالیز تابعی در مکانیک کوانتومی است. بسیاری از مسائل بهطور طبیعی به رابطهٔ بین یک کمیت و نرخ تغییراتش منجر میشوند. بسیاری از پدیدهها در طبیعت را میتوان به وسیله سیستمهای دینامیکی توصیف کرد؛ نظریه آشوب بهطور دقیق بررسی میکند که چگونه یک سیستم میتواند پیشبینی ناپذیر باشد و در حالی که همزمان رفتار قطعی خود را نیز حفظ میکند.
ریاضیات کاربردی[ویرایش]
ریاضیات کاربردی به دنبال روشهای ریاضیاتی است که اغلب در علوم، مهندسی، بازرگانی و صنعت به کار برده میشوند؛ لذا «ریاضیات کاربردی» یک علم ریاضیاتی است با دانش تخصصی. همچنین عبارت ریاضیات کاربردی تخصصی حرفه ای را توصیف میکند که بر روی مسائل عملی تمرکز کردهاست، ریاضیات کاربردی بر روی «فرمول بندی، مطالعه و استفاده از مدلهای ریاضیاتی» در علوم، مهندسی و دیگر حوزههایی که ریاضیات به کار میرود تمرکز میکند.
در عمل، کاربردهای عملی منجر به توسعه قضایای ریاضیاتی شده، که این قضایا خود، موضوع مطالعه در ریاضیات محض شدهاند، که در آن ریاضیات به هدف توسعه خود ریاضیات مطالعه میشود. ازین رو، فعالیت ریاضیات کاربردی بهطور حیاتی به تحقیقات در ریاضیات محض گره خوردهاست.
 |
 |
 |
 |
 |
||
| نظریه بازیها | دینامیک سیالات | آنالیز عددی | بهینهسازی | نظریه احتمال | آمار | رمز نگاری |
 |
 |
 |
 |
|||
| ریاضیات مالی | ریاضی فیزیک | شیمی ریاضیاتی | ریاضیات زیستی | ریاضیات اقتصاد | نظریه کنترل |
جوایز ریاضیاتی[ویرایش]

میتوان مدعی شد که مهمترین جایزه ریاضیاتی جایزهٔ فیلدز است،[۲۴][۲۵] که در سال ۱۹۳۶ تأسیس شد و در این سالها، هر چهار سال یک بار (به جز حدود جنگ جهانی دوم) به حداکثر ۴ ریاضیدان تعلق گرفتهاست (یکی از دارندگان مدال فیلدز مریم میرزاخانی است که اولین زن است که دارنده این مدال است). فیلدز اغلب به عنوان معادلی برای نوبل در ریاضیات در نظر گرفته شده.
جایزهٔ وولف در ریاضیات، در ۱۹۷۸ تأسیس شد و به هدف قدردانی از دستاوردهایی است که یک ریاضیدان در عمر خویش به آنها نایل گشته. جایزهٔ آبل در ۲۰۰۳ تأسیس شد. مدال چرن در ۲۰۱۰ معرفی شد برای قدردانی از دستاوردهای یک عمر. این جوایز برای اهمیت دادن به برخی کارهای نوآورانه، یا برای پیدا کردن راه حل برای مسائل مهم در یک شاخه خاص در نظر گرفته شدهاند.
لیستی از ۲۳ مسئله باز که به آنها «مسائل هیلبرت» میگویند در سال ۱۹۰۰ توسط ریاضیدان آلمانی داویت هیلبرت معرفی شد. این لیست به معروفیت زیادی بین ریاضیدانان دست یافت. حداقل نه تا از این مسائل اکنون حل شدهاند. لیست جدیدی از هفت مسئله مهم به نام «مسائل جایزه هزاره» نیز در سال ۲۰۰۰ منتشر شد. تنها یکی از آنها با لیست مسائل هیلبرت اشتراک دارد. جایزه حل هر مسئله در لیست جایزه هزاره ۱ میلیون دلار است.
خلاقیت و شهود ریاضیات[ویرایش]
نیاز به درستی و دقت به این معنا نیست که ریاضیات جایی برای خلاقیت ندارد. برعکس، بیشتر کارهای ریاضی فراتر از محاسبات بیدرنگ نیازمند حل مسئله هوشمندانه و کاوش شهودی دیدگاههای جدید است. افرادی که به ریاضیات تمایل دارند اغلب نه تنها خلاقیت را در ریاضیات میبینند، بلکه یک ارزش زیبایی شناختی را نیز میبینند که معمولاً به عنوان ظرافت توصیف میشود. کیفیتهایی مانند سادگی، تقارن، کامل بودن، و عمومیت به ویژه در اثباتها و تکنیکها ارزشمند است. جی.اچ. هاردی در کتاب «عذرخواهی یک ریاضیدان» معتقد است که این ملاحظات زیباشناختی به خودی خود برای توجیه مطالعه ریاضیات محض کافی هستند. او همچنین معیارهای دیگری مانند اهمیت، غیرمنتظره بودن و اجتناب ناپذیر بودن را که به زیباییشناسی ریاضی کمک میکنند، شناسایی کرد. پل اردوس این احساس را به شکل طعنه آمیزی با صحبت از «کتاب»، مجموعه ای فرضی الهی از زیباترین شواهد بیان کرد. کتاب (شواهدی از کتاب) در سال۱۹۹۸، با الهام از کتاب (جنگل) مجموعه ای از استدلالهای ریاضی مختصر و وحیانی است. برخی از نمونههای نتایج بهویژه ظریف شامل اثبات اقلیدس مبنی بر وجود بینهایت اعداد اول و تبدیل فوریه سریع برای تحلیل هارمونیک است. برخی بر این باورند که علم دانستن ریاضیات به معنای کماهمیت جلوه دادن هنر و تاریخ آن در هفت هنر سنتی لیبرال است. یکی از راههایی که این تفاوت دیدگاه نشان میدهد، در بحث فلسفی است که آیا نتایج ریاضی ایجاد میشوند (مانند هنر) یا کشف میشوند (مانند علم). محبوبیت ریاضیات تفریحی نشانه دیگری از لذت بسیاری از حل سوالات ریاضی است. در قرن بیستم، ریاضیدان (لی.ای. جی براور) حتی دیدگاهی فلسفی به نام شهودگرایی را آغاز کرد که در درجه اول ریاضیات را با فرآیندهای خلاقانه خاصی در ذهن شناسایی میکند. شهودگرایی به نوبه خود یکی از مزههای موضعی است که به عنوان ساختگرایی شناخته میشود، که تنها زمانی یک شی ریاضی را معتبر میداند که بتوان آن را مستقیماً ساخت، نه اینکه صرفاً توسط منطق بهطور غیرمستقیم تضمین شود. این امر سازندههای متعهد را به رد نتایج معین، بهویژه استدلالهایی مانند براهین وجودی مبتنی بر قانون میانه حذفشده، سوق میدهد. در نهایت، نه ساختگرایی و نه شهودگرایی جایگزین ریاضیات کلاسیک نشد و به مقبولیت اصلی دست یافتند. با این حال، این برنامهها انگیزهای برای پیشرفتهای خاصی مانند منطق شهودی و سایر بینشهای بنیادی داشتهاند که در نوع خود مورد قدردانی قرار میگیرند.
جستارهای وابسته[ویرایش]
منابع[ویرایش]
- ↑ «پارسی گویی و پارسی سره برابر پارسی واژه ریاضی». دریافتشده در ۲۰۲۲-۱۲-۰۳.
- ↑ ۲٫۰ ۲٫۱ "mathematics, n.". Oxford English Dictionary. Oxford University Press. 2012. Retrieved June 16, 2012.
The science of space, number, quantity, and arrangement, whose methods involve logical reasoning and usually the use of symbolic notation, and which includes geometry, arithmetic, algebra, and analysis.
- ↑ Kneebone, G.T. (1963). Mathematical Logic and the Foundations of Mathematics: An Introductory Survey. Dover. p. 4. ISBN 978-0-486-41712-7.
Mathematics ... is simply the study of abstract structures, or formal patterns of connectedness.
- ↑ ریاضیات.
- ↑ LaTorre, Donald R.; Kenelly, John W.; Biggers, Sherry S.; Carpenter, Laurel R.; Reed, Iris B.; Harris, Cynthia R. (2011). Calculus Concepts: An Informal Approach to the Mathematics of Change. Cengage Learning. p. 2. ISBN 978-1-4390-4957-0.
Calculus is the study of change—how things change, and how quickly they change.
- ↑ Ramana (2007). Applied Mathematics. Tata McGraw–Hill Education. p. 2.10. ISBN 978-0-07-066753-2.
The mathematical study of change, motion, growth or decay is calculus.
- ↑ Ziegler, Günter M. (2011). "What Is Mathematics?". An Invitation to Mathematics: From Competitions to Research. Springer. p. vii. ISBN 978-3-642-19532-7.
- ↑ Eves, p. 306
- ↑ Peterson, p. 12
- ↑ Dehaene, Stanislas; Dehaene-Lambertz, Ghislaine; Cohen, Laurent (Aug 1998). "Abstract representations of numbers in the animal and human brain". Trends in Neurosciences. 21 (8): 355–61. doi:10.1016/S0166-2236(98)01263-6. PMID 9720604.
- ↑ A study on the history of mathematics (۲۰۲۲-۰۴-۱۱). «ریاضی تجربی مهروماه». daneshland. دریافتشده در ۲۰۲۳-۰۷-۰۸.
- ↑ See, for example, Raymond L. Wilder, Evolution of Mathematical Concepts; an Elementary Study, passim
- ↑ Kline 1990, Chapter 1.
- ↑ Boyer 1991, "Mesopotamia" p. 24–27.
- ↑ Heath, Thomas Little (1981) [originally published 1921]. A History of Greek Mathematics: From Thales to Euclid. New York: Dover Publications. ISBN 978-0-486-24073-2.
- ↑ Boyer 1991, "Euclid of Alexandria" p. 119.
- ↑ Boyer 1991, "Archimedes of Syracuse" p. 120.
- ↑ Boyer 1991, "Archimedes of Syracuse" p. 130.
- ↑ Boyer 1991, "Apollonius of Perga" p. 145.
- ↑ Boyer 1991, "Greek Trigonometry and Mensuration" p. 162.
- ↑ Boyer 1991, "Revival and Decline of Greek Mathematics" p. 180.
- ↑ Luke Howard Hodgkin & Luke Hodgkin, A History of Mathematics, Oxford University Press, 2005.
- ↑ Clay Mathematics Institute, P=NP, claymath.org
- ↑ Monastyrsky 2001, p. 1: "The Fields Medal is now indisputably the best known and most influential award in mathematics."
- ↑ Riehm 2002, pp. 778–82.
کتابشناسی[ویرایش]
- Boyer, C.B. (1991). A History of Mathematics (2nd ed.). New York: Wiley. ISBN 978-0-471-54397-8.
- Courant, Richard; Robbins, Herbert (1996). What Is Mathematics?: An Elementary Approach to Ideas and Methods (2nd ed.). New York: Oxford University Press. ISBN 978-0-19-510519-3.
- du Sautoy, Marcus (25 June 2010). "Nicolas Bourbaki". A Brief History of Mathematics. BBC Radio 4. http://www.bbc.co.uk/programmes/b00stcgv.
- Einstein, Albert (1923). Sidelights on Relativity: I. Ether and relativity. II. Geometry and experience (translated by G.B. Jeffery, D.Sc. , and W. Perrett, Ph.D). E.P. Dutton & Co. , New York.
- Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Saunders. ISBN 978-0-03-029558-4.
- Kline, Morris (1990). Mathematical Thought from Ancient to Modern Times (Paperback ed.). New York: Oxford University Press. ISBN 978-0-19-506135-2.
- Monastyrsky, Michael (2001). "Some Trends in Modern Mathematics and the Fields Medal" (PDF). Canadian Mathematical Society. Retrieved July 28, 2006.
{{cite journal}}: Cite journal requires|journal=(help) - Oakley, Barbara (2014). A Mind For Numbers: How to Excel at Math and Science (Even If You Flunked Algebra). New York: Penguin Random House. ISBN 978-0-399-16524-5.
- Pappas, Theoni (June 1989). The Joy Of Mathematics (Revised ed.). Wide World Publishing. ISBN 978-0-933174-65-8.
- Peirce, Benjamin (1881). Peirce, Charles Sanders (ed.). "Linear associative algebra". American Journal of Mathematics (Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C.S. Peirce, of the 1872 lithograph ed.). 4 (1–4): 97–229. doi:10.2307/2369153. JSTOR 2369153. Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C. S. Peirce, of the 1872 lithograph ed. Google Eprint and as an extract, D. Van Nostrand, 1882, Google Eprint..
- Peterson, Ivars (2001). Mathematical Tourist, New and Updated Snapshots of Modern Mathematics. Owl Books. ISBN 978-0-8050-7159-7.
- Popper, Karl R. (1995). "On knowledge". In Search of a Better World: Lectures and Essays from Thirty Years. New York: Routledge. Bibcode:1992sbwl.book.....P. ISBN 978-0-415-13548-1.
- Riehm, Carl (August 2002). "The Early History of the Fields Medal" (PDF). Notices of the AMS. 49 (7): 778–72.
- Sevryuk, Mikhail B. (January 2006). "Book Reviews" (PDF). Bulletin of the American Mathematical Society. 43 (1): 101–09. Bibcode:1994BAMaS..30..205W. doi:10.1090/S0273-0979-05-01069-4. Retrieved June 24, 2006.
- Waltershausen, Wolfgang Sartorius von (1965) [first published 1856]. Gauss zum Gedächtniss. Sändig Reprint Verlag H. R. Wohlwend. ISBN 978-3-253-01702-5.
- Kline, M. , Mathematical Thought from Ancient to Modern Times (1973);
پیوند به بیرون[ویرایش]
| مجموعهای از گفتاوردهای مربوط به مخفف ریاضیات در ویکیگفتاورد موجود است. |
| معنای ریاضیات را در ویکیواژه، واژهنامهٔ آزاد، ببینید. |
| ویکیکتاب دارای کتابی پیرامون موضوع ویکیمدرسه/المپیاد ریاضی است |
| در ویکیانبار پروندههایی دربارهٔ ریاضیات موجود است. |
- فرهنگ جامع ریاضیات
- اطلس ریاضیات
- اریک ویستن، دنیای ریاضیات، http://www.mathworld.com دانشنامهٔ برخط ریاضیات.
- سیارهٔ ریاضی (به انگلیسی:Planet Math) دانشنامهٔ بر خط ریاضیات که هنوز در دست ساخت است. به دلیل استفاده از اجازهٔ GFDL امکان تبادل مقالات با ویکیپدیا وجود دارد. این دانشنامه از روش نشانگذاری TeX استفاده میکند.
- Metamath یک وبگاه و یک زبان که به شرح و بسط ریاضیات از پایه میپردازد.