توزیع لاگ-نرمال
|
تابع چگالی احتمال 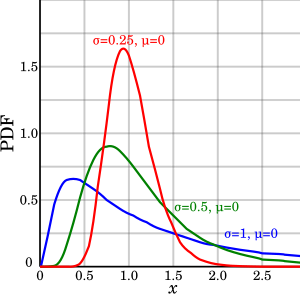 بعضی از توابع چگالی لاگ-نرمال با پارامتر همانی اما پارامترهای متفاوت | |||
|
تابع توزیع تجمعی  تابع توزیع تجمیعی توزیع لاگ-نرمال (با ) | |||
| نماد | |||
|---|---|---|---|
| پارامترها |
, | ||
| تکیهگاه | |||
| تابع چگالی احتمال | |||
| تابع توزیع تجمعی | |||
| چندک | |||
| میانگین | |||
| میانه | |||
| مُد | |||
| واریانس | |||
| چولگی | |||
| کشیدگی | |||
| آنتروپی | |||
| تابع مولد گشتاور | ، تنها برای اعداد با قسمت حقیقی غیرمثبت تعریف شدهاست متن را ببینید. | ||
| تابع مشخصه | نمایش به صورت مجانبی واگرا است، اما برای اهداف عددی کافی میباشد. | ||
| اطلاع فیشر | |||
| روش گشتاورها |
, | ||
توزیع لاگ-نرمال (به انگلیسی: log-normal یا lognormal) در نظریه احتمال نوعی توزیع احتمال پیوسته برای یک متغیر تصادفی است، که لگاریتم آن به صورت نرمال توزیع شدهاست.
از این رو اگر متغیر تصادفی X به صورت لاگ-نرمال توزیع شده باشد، آنوقت Y = ln(X) دارای توزیع نرمال است.[۱][۲][۳] به بیان دیگر، اگر Yدارای توزیع نرمال باشد، آنوقت تابع نمایی Y، یعنی X = exp(Y) دارای توزیع لاگ-نرمال است. متغیر تصادفی که به صورت لاگ-نرمال توزیع شدهاست، فقط مقادیر مثبت و حقیقی را میپذیرد.

توزیع لاگ-نرمال مدلی مفید و مناسب برای اندازهگیریها در علوم دقیق و مهندسی، مثل پزشکی، اقتصاد و دیگر عناوین است (مثلا انرژی، غلظت، طول، بازدهی مالی، و دیگر سنجهها).
به این توزیع، بعضی مواقع توزیع گالتون (به انگلیسی: Galton distribution) هم میگویند که به افتخار فرانسیس گالتون نامگذاری شدهاست.[۴] توزیع لاگ-نرمال با دیگر اسامی مثل مک آلیستر (به انگلیسی: McAlister), جبرات (به انگلیسی: Gibrat) و کاب – داگلاس (به انگلیسی: Cobb–Douglas) نیز مرتبط است.[۴]
یک فرایند لاگ-نرمال، یک فهم آماری از حاصلضرب چندین متغیر تصادفی مستقل است، که همه آنها مثبت هستند. این موضوع از طریق درنظرگرفتن قضیه حد مرکزی در دامنه لاگ قابل توجیه است. توزیع لاگ-نرمال همان توزیع احتمال با آنتروپی حداکثری برای متغیر تصادفی X است که در آن میانگین و واریانس ln(X) از قبل معین بودهاست.[۵]
تعاریف[ویرایش]
تولید و پارامترها[ویرایش]
فرض کنید که یک متغیر تصادفی با توزیع نرمال استاندارد باشد، و همچنین فرض کنید که و دو عدد حقیقی باشند. آنوقت توزیع متغیر تصادفی
یک توزیع لاگ-نرمال با پارامترهای و نامیده میشود. این پارامترها مقدار چشمداشتی (یا میانگین) و انحراف معیار برای لگاریتم طبیعی متغیر هستند، و نه خود .
پانویس[ویرایش]
- ↑ "List of Probability and Statistics Symbols". Math Vault (به انگلیسی). 2020-04-26. Retrieved 2020-09-13.
- ↑ Weisstein, Eric W. "Log Normal Distribution". mathworld.wolfram.com (به انگلیسی). Retrieved 2020-09-13.
- ↑ "1.3.6.6.9. Lognormal Distribution". www.itl.nist.gov. Retrieved 2020-09-13.
- ↑ ۴٫۰ ۴٫۱ Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1994), "14: Lognormal Distributions", Continuous univariate distributions. Vol. 1, Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-58495-7, MR 1299979
- ↑ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model" (PDF). Journal of Econometrics. 150 (2): 219–230. CiteSeerX 10.1.1.511.9750. doi:10.1016/j.jeconom.2008.12.014. Archived from the original (PDF) on 2016-03-07. Retrieved 2011-06-02. Table 1, p. 221.
منابع[ویرایش]
- مشارکتکنندگان ویکیپدیا. «Log-normal distribution». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۵ اکتبر ۲۰۲۰.









![{\displaystyle {\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\Big [}{\frac {\ln x-\mu }{{\sqrt {2}}\sigma }}{\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac1eb0032c5ba3af1ffbacf16a1a2ca275bdc657)




![{\displaystyle [\exp(\sigma ^{2})-1]\exp(2\mu +\sigma ^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b71d1959535c7b8ea00f302c3045c8dd941999b7)





![{\displaystyle \mu =\log \left({\frac {\operatorname {E} [X]^{2}}{\sqrt {\operatorname {Var} [X]+\operatorname {E} [X]^{2}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b659ac7cb997433f4571fb33cf42812e155c2ef1)
![{\displaystyle \sigma ^{2}=\log \left({\frac {\operatorname {Var} [X]}{\operatorname {E} [X]^{2}}}+1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c106691999762610071a2db63b5f4089a1d5aaa)




