توزیع گامای وارونه
|
تابع چگالی احتمال  | |||
|
تابع توزیع تجمعی 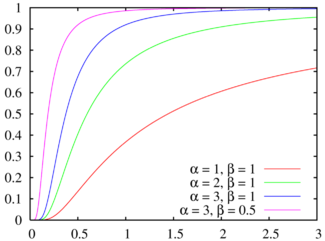 | |||
| پارامترها |
پارامتر شکل (عدد حقیقی) پارامتر مقیاس (real) | ||
|---|---|---|---|
| تکیهگاه | |||
| تابع چگالی احتمال | |||
| تابع توزیع تجمعی | |||
| میانگین | for | ||
| مُد | |||
| واریانس | for | ||
| چولگی | for | ||
| کشیدگی | for | ||
| آنتروپی | |||
| تابع مولد گشتاور | ; does not exist as عدد حقیقی function | ||
| تابع مشخصه | |||
در نظریه احتمالات و آمار، توزیع گامای وارونه توزیعی پیوسته و دو پارامتری است که تنها روی متغیرهای با مقدار مثبت تعریف میشود. بسیاری از کاربردهای توزیع گامای در مدل سازی بیزی است زمانی که واریانس توزیع نرمال نامعلوم است که به عنوان توزیع پسین حاشیهای ظاهر میشود.
تعریف ریاضی[ویرایش]
تعریف ریاضی تابع چگالی احتمال برای این توزیع عبارت است از:
جستارهای وابسته[ویرایش]
منابع[ویرایش]
- V. Witkovsky (2001) Computing the distribution of a linear combination of inverted gamma variables, Kybernetika 37(1), 79-90


















