کرل (ریاضیات)

در حساب برداری، کرل (به انگلیسی: Curl) یک عملگر برداری است که بیانگر چرخش میدان برداری ناشی از یک سطح بینهایتکوچک (به انگلیسی: infinitesimal) در فضای اقلیدسی سه بعدی است. کرل یک نقطه از این میدان را به کمک یک بردار نمایش میدهند که طول و جهت آن، نمایانگر بزرگی و محور چرخش بیشینه میدان برداری در آن نقطه است.[۱] کرل یک میدان برداری در یک نقطه را به طور صوری به صورت چگالی دوران یا چرخش آن میدان برداری در نقطه مورد نظر نیز تعریف میکنند.
تعریف[ویرایش]
کرلِ میدان برداری A که با هر یک از نمادهای ، ، ، ، ، و یا curl A نمایش داده میشود، برداری است که اندازه آن حداکثر گردش خالص A در واحد سطح است وقتیکه اندازهٔ سطح به سوی صفر میل میکند و جهت آن جهت عمود سطح است زمانی که سطح طوری جهت داده شدهباشد که گردش خالص را حداکثر نماید.
که این تعریف را میتوان به صورت زیر نوشت:
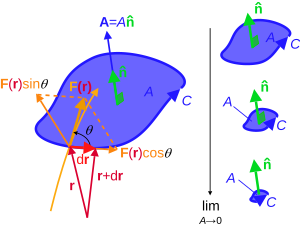
سمت راست انتگرال خطی روی ناحیهی بینهایت کوچکِ C است که به سمت صفر میل میکند. و n، بردار نرمال ناحیهی C است.
میدان برداری بدون کرل، میدان غیرگردشی یا میدان ناگردان یا میدان ذخیرهشونده نامیده میشود.
در عمل فرمول بالا به ندرت برای محاسبهی کرل استفاده میشود. از فرمول زیر برای محاسبهی آن استفاده میشود:
که معادل است با دترمینان ماتریسی زیر:
نمایش تنسوری آن به صورت زیر است:
در اینجا مطابق شیوهٔ نگارش اینشتین، اندیس تکرارشونده نشانهٔ جمع بر اندیس است و عملگر مشتق (دل) است.
تعبیر فیزیکی[ویرایش]
نام کرل به این دلیل انتخاب شده است که کرل یک میدان برداری در یک نقطه، معیاری است که آن میدان برداری چه مقدار چرخش حول آن نقطه دارد. برای درک مفهوم کرل فرض کنید که در کنار یک استخر ایستادهاید و پرّهای کوچک (مثلاً یک چوبپنبه بههمراه چند خلال دندان که در آن فرورفتهاند) در استخر انداختهاید. اگر پره در نقطهای قرار بگیرد که کرل در آن غیرصفر است، شروع به چرخیدن میکند. در این مثال سرعت آب میدان برداری مورد نظر است و پره، کرل این میدان برداری را در هر نقطه اندازه میگیرد.[۲]
مثال ها[ویرایش]
مثال یک[ویرایش]
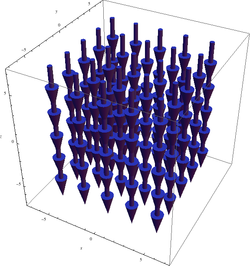
میدان برداری زیر را در نظر بگیرید:

اگر بردارهای میدان، نیرو های وارد بر جسم حاضر در یک نقطه را نشان دهند.در اثر نیرو آن جسم شروع به چرخش ساعتگرد به دور خودش میکند فارغ از اینکه جسم در کجا قرار دارد:
- کرل میدان مورد نظر، میدان یکنواخت در جهت منفی z است. نتیجهی به دست آمده را میتوانستیم با استفاده از قانون دست راست پیشبینی کنیم. یکنواخت بودن کرل باعث میشود که جسم قرار داده شده در هرجای میدان با سرعت چرخشی مشخصی به دور خودش بگردد بدون توجه به این که کجای میدان قرار دارد.
- نمودار کرلِ میدانِ مثالِ یک، به صورت زیر است:
برخی خواص[ویرایش]
جستارهای وابسته[ویرایش]
- عملگر مشتق (دِل)
- گرادیان
- واگرایی
- لاپلاسین
پانویس[ویرایش]
برای مطالعه بیشتر[ویرایش]
- Korn, Granino Arthur and Theresa M. Korn (January 2000). Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. New York: Dover Publications. pp. 157–160. ISBN 0-486-41147-8.
- Schey, H. M. (1997). Div, Grad, Curl, and All That: An Informal Text on Vector Calculus. New York: Norton. ISBN 0-393-96997-5.
پیوندهای بیرونی[ویرایش]
- "Curl", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- "Vector Calculus: Understanding Circulation and Curl – BetterExplained". betterexplained.com. Retrieved 2020-11-09.
- "Divergence and Curl: The Language of Maxwell's Equations, Fluid Flow, and More". June 21, 2018 – via YouTube.















