سیاهچاله


سیاهچاله (به انگلیسی: Blackhole) ناحیهای در فضا-زمان با گرانشی بسیار نیرومند است که هیچ چیز حتی ذرات و تابشهای الکترومغناطیسی مانند نور نمیتوانند از میدان گرانش قدرتمند آن بگریزند.[۶] نظریه نسبیت عام آلبرت اینشتین بیان میکند که یک جرم به اندازهٔ کافی فشرده شده، میتواند سبب تغییر شکل و خمیدگی فضا-زمان و تشکیل سیاهچاله شود. مرز این ناحیه از فضا زمان که هیچ چیزی پس از عبور از آن نمیتواند به بیرون برگردد را افق رویداد مینامند. صفت «سیاه» در نام سیاهچاله برگرفته از این واقعیت است که همهٔ نوری را که از افق رویداد آن میگذرد به دام میاندازد؛ از این دیدگاه سیاه چاله رفتاری شبیه به جسم سیاه در ترمودینامیک دارد.[۷][۸] از سوی دیگر نیز، نظریه میدانهای کوانتومی در فضازمان خمیده پیشبینی میکند که افقهای رویداد نیز تابشی به نام تابش هاوکینگ گسیل میکنند که طیف آن همانند طیف جسم سیاهی است که دمای آن با جرمش نسبت وارونه دارد. میزان دما در مورد سیاهچالههای ستارهای در حد چند میلیاردم کلوین است و از این رو ردیابی آن دشوار است.
اجسامی که به دلیل میدان گرانشی بسیار قوی اجازهٔ گریز به نور نمیدهند برای اولین بار در سده ۱۸ (میلادی) توسط جان میچل و پیر سیمون لاپلاس مورد توجه قرار گرفتند. نخستین راه حل نوین نسبیت عام که در واقع ویژگیهای یک سیاهچاله را توصیف مینمود در سال ۱۹۱۶ میلادی توسط کارل شوارتزشیلد کشف شد.[۹][۱۰]هر چند تعبیر آن به صورت ناحیهای گریزناپذیر از فضا، تا چهار دهه بعد به خوبی درک نشد، برای دورهای طولانی این چالش مورد کنجکاوی ریاضیدانان بود تا اینکه در میانه دهه ۱۹۶۰، پژوهشهای نظری نشان داد که سیاهچالهها به راستی یکی از پیشبینیهای ژنریک نسبیت عام هستند. یافتن ستارگان نوترونی باعث شد تا وجود اجرام فشرده شده بر اثر رمبش گرانشی به عنوان یک واقعیت امکانپذیر فیزیکی مورد علاقه دانشمندان قرار گیرد.[۱۱] اینگونه برداشت میشود که سیاهچالههای ستارهای در جریان فروپاشی ستارههای بزرگ در یک انفجار ابرنواختری در پایان چرخه زندگیشان به وجود میآیند. جرم یک سیاهچاله پس از شکلگیری میتواند با دریافت جرم از پیرامونش افزایش یابد. با جذب ستارگان پیرامون و بهم پیوستن سیاهچالههای گوناگون، سیاهچالههای کلان جرم با جرمی میلیونها برابر خورشید تشکیل میشوند.[۱۲]
سیاهچاله به دلیل اینکه نوری از آن خارج نمیگردد نامرئی است، اما میتواند بودن خود را از راه کنش و واکنش با ماده پیرامون خود نشان دهد. از راه بررسی برهمکنش میان ستاره دوگانه با همدم نامرئیشان، اخترشناسان نامزدهای احتمالی بسیاری برای سیاهچاله بودن در این منظومهها شناسایی کردهاند. این باور جمعی در میان دانشمندان رو به گسترش است که در مرکز بیشتر کهکشانها یک سیاهچاله کلانجرم وجود دارد. برای نمونه، دستاوردهای ارزشمندی بازگوی این واقعیت است که در مرکز کهکشان راه شیری ما نیز یک سیاهچاله کلان جرم با جرمی بیش از چهار میلیون برابر جرم خورشید وجود دارد.[۱۳]
در دهم ماه آوریل سال ۲۰۱۹ برای اولین بار عکسی از یک سیاهچاله ثبت و انتشار یافت.[۱۴]
تاریخچه[ویرایش]

ابداع واژه «کرمچاله»[۱۵] و «سیاهچاله فضایی»[۱۶] به جان ویلر نسبت داده شدهاست. با اینحال، این مفهوم از مدتها قبل به صورتهای متفاوتی مطرح بودهاست.
مفهوم جسمی که آن قدر پرجرم است که حتی نور هم نمیتواند از آن بگریزد، نخستین باراز سوی زمینشناسی به نام جان میچل در سال ۱۷۸۳ در نامهای که برای هنری کاوندیش از انجمن سلطنتی نوشته بود، مطرح شد. در آن زمان مفهوم قانون گرانش نیوتن و مفهوم سرعت گریز شناخته شده بودند. طبق محاسبات میشل جسمی با شعاع خورشیدی و چگالی ۵۰۰ برابر در سطح خود سرعت گریزی بیش از سرعت نور خواهد داشت و بنابراین غیرقابل مشاهده خواهد بود. به بیان او:
اگر شعاع کرهای مشابه خورشید بوده ولی چگالی آن ۵۰۰ بار از آن بزرگتر باشد، جسمی که از ارتفاع بینهایت به سمت آن سقوط میکند در سطح آن سرعتی بیش ازسرعت نور به دست میآورد، و اگر فرض کنیم نور با نیروی مشابهی به سمت ستاره کشیده شود، آنگاه همه نوری که از چنین جسمی ساطع میشود به ناچار به وسیله گرانش آن به سمت خود ستاره بازمیگردد.
— جان میچل
در سال ۱۷۹۶ پیر سیمون لاپلاس، ریاضیدان فرانسوی همان ایده را در ویرایش اول و دوم کتاب خود به نام آشکارسازی نظام جهان مطرح کرد. این مطالب در ویرایشهای بعدی کتاب حذف شد.[۱۸][۱۹] مفهوم این ستارههای تاریک در سده ۱۹ (میلادی) توجه چندانی را به خود جلب نکرد زیرا فیزیک دانان نمیتوانستند درک کنند که نور که یک موج و بدون جرم است چگونه ممکن است تحت تأثیر نیروی گرانش قرار گیرد.
نسبیت عام[ویرایش]
| بخشی از سری مقالات در مورد: |
| نسبیت عام |
|---|
 |
در سال ۱۹۱۵ آلبرت اینشتین که پیش تر نشان داده بود گرانش نور را تحت تأثیر قرار میدهد، نظریهٔ گرانش خود به نام نسبیت عام را مطرح کرد. چند ماه بعد کارل شوارتزشیلد با معرفی متریک شوارتسشیلد پاسخی برای معادلات میدان اینشتین ارائه نمود که میدان گرانشی ذرات نقطهای و کروی را توصیف میکرد.[۲۰] چند ماه پس از شوارتزشیلد، ژوهانس دروست - که از شاگردان هندریک لورنتز بود - به صورت جداگانه همان پاسخ را برای ذرات نقطهای به دست آورد و بحث مفصل تری در مورد ویژگیهای آن نمود.[۲۱] این پاسخ در شعاعی که امروزه شعاع شوارتزشیلد نامیده میشود رفتاری غیرعادی نمایش میداد؛ زیرا در این شعاع، معادله تکینه میشود و برخی از اجزای آن مقدار بینهایت خواهند داشت. در آن زمان ماهیت این سطح به درستی فهمیده نشده بود. در سال ۱۹۲۴ آرتور استنلی ادینگتون نشان داد که با تغییر مختصات میتوان تکینگی را بر طرف نمود. هر چند که تا سال ۱۹۳۳ طول کشید تا ژرژ لومتر متوجه شد که مقدار بینهایت این معادله در شعاع شوارتزشیلد در واقع یک تکینگی ریاضی است و جنبه فیزیکی ندارد.[۲۲] این شعاع امروزه به عنوان شعاع افق رویداد یک سیاهچاله غیرچرخشی شناخته میشود.
در سال ۱۹۳۰ سوبرامانیان چاندراسخار، اختر فیزیک دان هندی محاسبه نمود که یک جسم الکترون تباهیده غیر چرخنده که جرم آن از حدی (که بعدها به نام حد چاندراسخار نامیده شد و ۱٫۴ برابر جرم خورشید است) بیشتر باشد هیچ جواب پایداری ندارد.[۲۳] ادعای وی از سوی هم دورهایهای وی همچون ادینگتون و لو لانداو مورد مخالفت قرار گرفت. آنها ادعا میکردند که مکانیزمی ناشناخته وجود دارد که از فروپاشی این اجرام جلوگیری میکند.[۲۴] ادعای آنها تا حدودی درست بود زیرا یک کوتوله سفید که جرم آن اندکی از حد چاندراسخار بزرگتر باشد پس از فروپاشی به یک ستاره نوترونی تبدیل میشود[۲۵] که بنا بر اصل طرد پاولی، وضعیتی پایدار دارد، اما در سال ۱۹۳۹ رابرت اوپنهایمر و دیگران پیشبینی کردند که ستارههای نوترونی که جرمی بیشتر از سه برابر جرم خورشید دارند به دلایلی که توسط چاندراسخار ارائه شد، به سیاهچاله فروپاشی میشوند و نتیجهگیری کردند که هیچ سازوکار فیزیکی نمیتواند از فروپاشی برخی ستارگان به سیاهچاله جلوگیری نماید.[۲۶]
عصر طلایی[ویرایش]
در سال ۱۹۵۸، دیوید فینکلشتین سطح شوارتز شیلد را به عنوان یک افق رویداد معرفی نمود، «یک غشای کاملاً یک جهته که تأثیرات سببی تنها از یک سو از آن عبور میکنند.»[۲۷] این مطلب تناقض صریحی با نتایج اوپنهایمر ندارد بلکه آن را گسترش میدهد تا ناظرین در حال سقوط به سیاهچاله را نیز شامل شود.[۲۸]
این نتایج مقارن بود با آغاز عصر طلایی نسبیت عام که در آن تحقیقات دربارهٔ نسبیت عام و سیاهچالهها رونق فراوان یافت همچون کشف تپ اخترها در سال ۱۹۶۷ که در سال ۱۹۶۹ نشان داده شد که ستارههای نوترونی چرخنده با سرعت چرخش بالا هستند،[۲۹] به این فرایند کمک کرد.[۳۰][۳۱] تا آن زمان ستارگان نوترونی مانند سیاهچالهها تنها در حوزه تئوری مطرح بودند اما کشف تپ اخترها نشان داد که واقعیت فیزیکی نیز دارند و باعث شد تا علاقه شدیدی به انواع اجسام فشردهای که ممکن است بر اثر رمبش گرانشی تشکیل شوند برانگیخته شود. با کشف اختروش (کوازار)ها که انرژی خروجی بسیار بزرگ آنها این احتمال را مطرح نمود که ممکن است مکانیزم بهوجود آورنده این انرژی، رمبش گرانشی باشد این علاقه رو به فزونی نهاد.[۳۲]
در این دوره جوابهای کلی تری نیز برای معادله سیاهچاله پیدا شد. روی کِر جواب دقیقی برای یک سیاه چاله چرخان به دست آورد. دو سال بعد ازرا نیومن یک جواب متقارن محوری برای سیاهچالهای که هم چرخان باشد و هم دارای بار الکتریکی باشد کشف نمود.[۳۳] در نتیجه کارهای ورنر اسرائیل،[۳۴] براندون کارتر[۳۵][۳۶] و دیوید رابینسون[۳۷] نظریه بدون مو ظهور کرد که با استفاده از پارامترهای متریک کر-نیومن، جرم، تکانه زاویهای و بار الکتریکی یک سیاهچاله ثابت را توصیف نمود.[۳۸]
ویژگیها و ساختار[ویرایش]

نظریه «بدون مو» ی جان ویلر بیان میکند که هر سیاهچاله پس از اینکه تشکیل شد و به وضعیت پایداری رسید، تنها سه خاصیت فیزیکی مستقل دارد: جرم، بار الکتریکی، و اندازه حرکت زاویهای. از نظر مکانیک کلاسیک (غیر کوانتومی)[۳۸] دو سیاهچاله که دارای مقادیر یکسانی برای سه ویژگی یاد شده باشند، نامتمایزاند.
این سه ویژگی، ویژگیهای خاصی هستند زیرا از بیرون سیاهچاله قابل مشاهدهاند؛ مثلاً یک سیاهچاله باردار همچون هر جسم باردار دیگری بارهای همنام را دفع میکند. به طریق مشابهی مجموع جرم درون کرهای که یک سیاهچاله را دربرمی گیرد از طریق همتای قانون گاوس در مورد نیروهای گرانشی یعنی جرم ایدیام نسبیت عام از فواصل بسیار دور اندازهگیری نمود.[۳۹] به همین ترتیب تکانه زاویهای یک سیاهچاله را نیز میتوان از راه کشش چارچوب توسط میدان مغناطیس گرانشی به دست آورد.
وقتی جسمی به درون سیاهچالهای سقوط میکند تمام اطلاعات فیزیکی مربوط به شکل جرم یا توزیع بار سطحی آن بهطور یکنواخت در امتداد افق رویداد توزیع میشود و از دید ناظر خارجی گم میشود. این رفتار افق رویداد به عنوان سیستم پراکنده ساز نامیده میشود و به آنچه در یک غشای کشی رسانا با اصطکاک و مقاومت الکتریکی رخ میدهد شباهت بسیار دارد.[۴۰] این تفاوت از آن دسته نظریههای میدانی مانند الکترودینامیک کوانتومی است که به دلیلی معکوسپذیری در زمان هیچ اصطکاک یا مقاومتی در سطح میکروسکوپیک ندارند؛ زیرا یک سیاهچاله در نهایت با سه پارامتر به حالت پایدار میرسد و هیچ راهی وجود ندارد که از گم شدن اطلاعات مربوط به شرایط اولیه اجتناب نمود: میدانهای گرانشی و الکتریکی سیاهچاله اطلاعات بسیار اندکی در بارهٔ آنچه وارد سیاهچاله شدهاست میدهند. اطلاعات گم شده شامل هر کمیتی است که از فاصله دور از افق رویداد یک سیاهچاله قابل اندازهگیری نیستند. از جمله میتوان از عدد باریونی و عدد لپتونی کل نام برد. این موضوع تا اندازهای گیجکنندهاست که از آن به پارادوکس گم شدن اطلاعات سیاهچاله یاد میشود.[۴۱][۴۲]
خواص فیزیکی[ویرایش]
سادهترین نوع سیاهچالهها آنهایی هستند که تنها جرم دارند و بار الکتریکی و تکانه زاویهای ندارند. این سیاهچالهها را اغلب با نام سیاهچالههای شوارتسشیلد مینامند که بر گرفته از نام کارل شوارتزشیلد است که جوابی برای معادلات میدانی اینشتین در سال ۱۹۱۶ ارائه نمود.[۲۰] بنا بر قضیه بیرخوف در نسبیت عام، تنها جواب خلأ است که متقارن کروی است. این بدان معنی است که تفاوتی میان میدان گرانشی یک سیاهچاله و یک جسم کروی با همان جرم وجود ندارد؛ بنابراین سیاهچاله تنها در محدوده نزدیک به افق آن است که همه چیز حتی نور را به درون میکشد و در فواصل دورتر کاملاً مانند هر جسم دیگری با همان میزان جرم رفتار میکند.[۴۳]
راه حلهایی برای معادلات اینشتین که سیاهچالههای کلی تری را توصیف میکنند نیز وجود دارند؛ مثلاً متریک رایسنر-نوردشتروم سیاهچالههای باردار و متریک کر سیاهچالههای چرخان را توصیف میکنند. کلیترین جواب موجود برای سیاهچالههای ثابت متریک کر-نیومن است که سیاهچالههایی را توصیف میکند که هم بار الکتریکی وهم تکانه زاویهای دارند.[۴۴]
درحالیکه جرم سیاهچاله میتواند هر مقداری داشته باشد، بار و تکانه زاویهای آن توسط جرم محدود میشوند. چنانچه واحدهای پلانک را بکار ببریم، کل بار الکتریکی Q و مجموع تکانه زاویهای J در این رابطه صدق میکنند(M جرم سیاهچالهاست): . سیاهچالههایی که نابرابری فوق را اشباع میکنند، سیاهچالههای اکسترمال نامیده میشوند. جوابهایی نیز برای معادلات اینشتین موجودند که این نابرابری را نقض میکنند اما این جوابها افق رویداد ندارند. این جوابها را تکینگیهای برهنه مینامند که از بیرون قابل مشاهدهاند و در نتیجه نمیتوانند فیزیکی باشند. فرضیه سانسور کیهانی شکلگیری چنین تکینگیهایی را در جریان رمبش نامحتمل میشمرد.[۴۵]
به دلیل قدرت نسبی الکترومغناطیس سیاهچالههایی که از رمبش ستارگان تشکیل میشوند تمایل دارند که بار تقریباً خنثی ستاره را حفظ کنند. اما انتظار میرود که چرخش، یک ویژگی مشترک در اجسام فشرده باشد. نامزد سیاهچاله قرار گرفته در دوتایی پرتو ایکس جیآراس ۱۹۱۵+۱۰۵[۴۶] به نظر میرسد که تکانه زاویهای نزدیک به حداکثر مقدار مجاز داشته باشد.
افق رویداد[ویرایش]
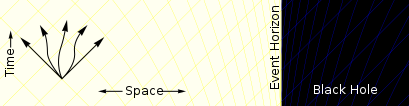 در نواحی دور از یک سیاهچاله یک ذره میتواند در هر جهتی حرکت کند و تنها محدود به سرعت نور است. |
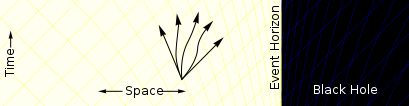 در فواصل نزدیکتر به سیاهچاله فضا-زمان شروع به خمش میکند. مسیرهایی که به سیاهچاله ختم میشوند از مسیرهایی که از آن دور میشوند بیشترند.[۴۷] مجموعه مسیرهای ممکن یا به عبارت دقیقتر قیف نور آینده که شامل همه خطهای جهانی ممکن (در این نمودار با شبکههای زرد-آبی نمایش داده شدهاند), بدین شکل در مختصات ادینگتون-فینکلشتین خم میشوند (نمودار یک نسخه کارتونی از نمودار مختصات فینکلشتین-ادینگتون است), اما در سایر مختصاتها قیفهای نوری بدین شکل خم نمیشوند؛ مثلاً درمختصات شوارتزشیلد چنانچه به افق رویداد نزدیک شویم، نازک میشوند اما خم نمیگردند، و در مختصات کروسکال-سزکرس قیفهای نوری شکل یا جهت گیریشان را تغییر نمیدهند. |
 در داخل افق رویداد تمام مسیرها ذره را به سمت مرکز سیاهچاله سوق میدهند. ذره دیگر امکان گریز نخواهد داشت. |
مهمترین ویژگی که یک سیاهچاله را تعریف میکند پیدایش افق رویداد است. افق رویداد به شکل کروی یا تقریباً کروی با شعاع شوارتزشیلد حول نقطه مرکزی سیاهچالهاست. این کره ناحیهای از فضا زمان است که عبور نور و ماده از آن تنها در یک جهت و به طرف درون آن ممکن است. درون این کره سرعت گریز از سرعت نور بیشتر خواهد بود، و از آنجاییکه هیچ جسمی توانایی حرکت با سرعت بیشتر از سرعت نور را ندارد، هیچ جسمی توانایی گریز از این منطقه را ندارد. هر جرم یا انرژی که به یک سیاه چاله نزدیک شود، در داخل فاصله معینی که افق رویداد آن خوانده میشود، بهطور مقاومت ناپذیری به درون سیاه چاله کشیده میشود. نوری که از اطراف یک سیاه چاله عبور میکند، اگر به افق رویداد نرسد، روی مسیری منحنی شکل از کنار آن میگذردو اگر به افق رویداد برسد، در سیاه چاله سقوط میکند. افق رویداد را از این رو به این نام میخوانند که از درون آن اطلاعات راجع به آن رخداد به مشاهدهکننده نمیرسد و مشاهدهکننده نمیتواند یقین حاصل کند که این اتفاق رخ دادهاست.[۴۸]
آنگونه که در نسبیت عام پیشبینی میشود، حضور یک جسم باعث خمش فضا-زمان میشود به گونهای که مسیرهایی که ذرات طی میکنند به سمت جرم خمیده میشوند.[۴۹] در افق رویداد یک سیاهچاله این تغییر شکل به اندازهای قوی میشود که هیچ مسیری که از سیاهچاله دور شود وجود نخواهد داشت.
از دید یک ناظر دور زمان در نزدیکی سیاهچاله کندتر از نقاط دورتر خواهد گذشت.[۵۰] این پدیده به نام اتساع زمان نامیده میشود. شیئی که به افق رویداد نزدیک شود به نظر خواهد رسید که هرچه نزدیکتر میگردد از سرعت آن کاسته میشود و زمانی بینهایت طول خواهد کشید تا به آن برسد.[۵۱] و چون تمام فرایندهای این ذره کندتر میشود، نوری که منتشر میکند تاریکتر و قرمزتر خواهد شد که این اثر به نام انتقال به سرخ گرانشی نامیده میشود.[۵۲] سرانجام در نقطهای که به افق رویداد میرسد این جسم کاملاً تاریک و غیرقابل مشاهده میشود.
ازسوی دیگر ناظری که به درون سیاهچاله سقوط میکند، در زمانی که افق رویداد را رد میکند، متوجه هیچکدام از این تأثیرات نخواهد شد. طبق ساعت خودش افق رویداد را در زمانی متناهی رد میکند. اگرچه هرگز نمیتواند بفهمد که دقیقاً در چه زمانی از افق رویداد رد شدهاست؛ زیرا غیرممکن است که بتوان با مشاهدات محلی، موقعیت افق رویداد را تعیین کرد.[۵۳]
افق رویداد یک سطح جامد نیست و مانع ورود ماده یا تابشی که به سمت ناحیه داخل آن در حرکت است نمیشود. در واقع افق رویداد یک ویژگی تعریف شده سیاهچالهاست که حدود سیاهچاله را مشخص میکند. علت سیاه بودن افق رویداد هم این است که هیچ پرتوی نور یا تابش دیگری نمیتواند از آن بگریزد. از این رو افق رویداد هر آنچه را که درون آن اتفاق میافتد از دید دیگران پنهان نگه میدارد.
شکل افق رویداد یک سیاهچاله همیشه تقریباً کروی است. این تنها در مورد فضاهای چهار بعدی صادق است. در ابعاد بالاتر امکان توپولوژیهای پیچیده تری مانند حلقه سیاه پدید میآید.[۵۴][۵۵][۵۶] برای سیاهچالههای ایستای غیر چرخان این شکل کاملاً کروی است و برای سیاهچالههای چرخان کمی بیضوی است.
تکینگی گرانشی[ویرایش]
براساس نسبیت عام، مرکز یک سیاهچاله یک نقطه تکینگی گرانشی است، ناحیهای که در آن خمیدگی فضا زمان به بینهایت میشود.[۵۷]بدین معنا که زمان بی معنا میگردد و جاذبه به بینهایت مبدل میگردد. برای یک سیاهچاله غیر چرخان این ناحیه به شکل یک نقطه منفرد و برای یک سیاهچاله کر به شکل یک تکینگی حلقوی روی صفحه چرخش خواهد بود.[۵۸] در هردوی موارد حجم ناحیه تکینگی صفر است.[۵۹] به همین دلیل چگالی ناحیه تکینگی، بینهایت خواهد بود.
ناظری که به درون یک سیاهچاله شوارتزشیلد سقوط میکند (یعنی بدون بار و تکانه زاویهای) به محض اینکه از افق رویداد بگذرد دیگر نمیتواند در مقابل سرازیر شدن به سوی نقطه تکینگی جلوگیری کند. این ناظر میتواند تنها تا میزان محدودی زمان سقوطش را با سرعت گرفتن در جهت مخالف طولانیتر کند اما سرانجام به نقطه تکینگی سقوط خواهد کرد.[۶۰] زمانی که به این نقطه برسد به چگالی بینهایت برخورد میکند و جرم آن به جرم سیاهچاله افزوده میشود. البته پیش از این اتفاق در طی فرایندی که به اسپاگتی سازی یا اثر نودلی معروف است، اجزای وی بر اثر نیروهای جزر و مدی در حال گسترش از هم گسیخته میشود.[۶۱]
در مورد یک سیاهچاله باردار (راه حل رایسنر-نوردستروم) یا چرخان (راه حل کر) میتوان از تکینگی اجتناب نمود. چنانچه این جوابها را تا حد امکان گسترش دهیم امکان فرضی خروج از سیاه چاله به یک فضا-زمان متفاوت خود را نمایان میسازد. در این صورت سیاهچاله به صورت یک کرمچاله عمل میکند.[۶۲] اما فرضیه سفر به دنیاهای دیگر تنها به صورت فرضیه میماند زیرا آشفتگی امکان آن را ازبین میبرد.[۶۳] همچنین این فرضیه مطرح میشود که منحنیهای زمان گونه بسته را در اطراف تکینگی دنبال کرد و به گذشته خود فرد سفر کرد که در نهایت به طرح مشکلاتی در قانون علیت مانند سفر در زمان میانجامد.[۶۴]
پیدایش تکینگی هاگی در نسبیت عام را عموماً نشانهای از شکست این نظریه میپندارند؛[۶۵] اما این شکست برخلاف انتظار نیست. این شکست در مواردی رخ میدهد که بخواهیم این کنشها را با استفاده از تأثیرات مکانیک کوانتومی، ناشی از چگالی بسیار بالا و سرانجام تعامل ذرات توصیف کنیم. تا کنون این امر میسر نشدهاست که بتوانیم تأثیرات گرانشی و کوانتومی را در یک تئوری با هم ترکیب نمود. مورد انتظار عموم این است که یک تئوری گرانش کوانتومی خواهد توانست ویژگی سیاهچالهها را بدون تکینگی بیان کند.[۶۶][۶۷]
کره فوتونی[ویرایش]

کره فوتونی، محدودهای کروی با ضخامت صفراست. فوتونهایی که در طول مسیر مماس (در امتداد تانژانتها) بر این کره حرکت میکنند در مداری دایرهای گرد آن به دام میافتند. در سیاهچالههای غیرچرخشی شعاع فوتون کره یک و نیم برابر شعاع افق رویداد (شوارتزشیلد) است. این مدارها از نظر دینامیکی ناپایدار اند و به همین جهت هر آشفتگی کوچکی (مثل سقوط یک ذره مادی) در طول زمان گسترش مییابد و به صورت حرکت پرتابی به خارج سیاهچاله یا به شکل حلزونی در نهایت از افق رویداد میگذرد.[۶۸]
درحالیکه نور هنوز میتواند از داخل کره فوتونی بگریزد، هر نوری که از کره فوتونی عبور کند در یک حرکت پرتابی به داخل سیاهچاله کشیده میشود؛ بنابراین نوری که از درون کره فوتونی به ما میرسد باید از اجسامی تابیده شده باشد که درون کره فوتونی هستند اما هنوز به افق رویداد نرسیدهاند.[۶۸]
سایر اجرام فشرده همچون ستارههای نوترونی نیز میتوانند کرههای فوتونی داشته باشند.[۶۹] این امر ناشی از این حقیقت است که میدان گرانشی یک شی به اندازه واقعی آن بستگی ندارد، از این رو هر جسم که کوچکتر از ۱٫۵ برابر شعاع شوارتزشیلد متناظر با جرمش باشد میتواند کره فوتونی داشته باشد.[نیازمند منبع]
ارگوسفر[ویرایش]
سیاهچالههای چرخان در درون ناحیهای از فضا و زمان محصورند که در آن ثابت ماندن غیرممکن است. این ناحیه را ارگوسفر مینامند. این پدیده ناشی از فرایندی به نام کشش چارچوب است. تئوری نسبیت عام پیشبینی میکند که هر جسم در حال چرخش تمایل دارد که فضا-زمان اطراف نزدیک خود را بکشد. هر جسم نزدیک به جسم چرخان تمایل خواهد داشت که در جهت چرخش حرکت کند. برای یک سیاهچاله چرخان در نزدیکی افق رویدادش این اثر به اندازهای قدرتمند میشود که جسم مجبور است که با سرعتی بالاتر از سرعت نور در جهت مخالف بچرخد تا تنها بتواند ثابت بماند.[۷۰]
ارگوسفر یک سیاهچاله از درون به افق رویداد میرسد و از بیرون به یک کره بیضوی که در قطبش با کره افق رویداد مماس میشود و قسمت استوایی آن بسیار پهنتر از سایر قسمتها است پایان مییابد. این مرز خارجی ارگوسفر را گاهی سطح ارگو مینامد.
اجسام و تابش میتوانند بهطور عادی از ارگوسفر بگریزند. بنا بر فرایند پنروز اجسامی که از ارگوسفر خارج میشوند ممکن است انرژی بیشتر از انرژی ورودشان داشته باشند. این انرژی از انرژی چرخشی سیاهچاله گرفته میشود و باعث کندتر شدن سرعت آن میشود.[۷۱]
ذخیره اطلاعات[ویرایش]
استیون هاوکینگ فیزیکدان ممتاز بریتانیایی در اوت ۲۰۱۵ گفت که سیاهچالهها اطلاعات مربوط به چیزهایی که در درون آنها سقوط میکند را ذخیره میکنند. ابتدا تصور میشد که این اطلاعات از بین میرود، اما معلوم شد که این ناقض قوانین فیزیک کوانتوم خواهد بود. همزمان، قوانین مکانیک کوانتومی حکم میکند که همه چیز در جهان ما میتواند به اطلاعات تجزیه شود، برای مثال، به یک رشته صفر و یک. اما براساس نظریه نسبیت عام اینشتین، این اطلاعات باید نابود شود. این معما به پارادوکس اطلاعات معروف است. به باور هاوکینگ این اطلاعات ممکن است اصلاً وارد سیاهچاله نشود، بلکه در سرحد آن باقی بماند. براساس این قوانین، این اطلاعات هرگز محو نمیشود، نه حتی وقتی توسط سیاهچاله بلعیده میشود. او گفت: "برخلاف آنچه انتظار میرود این اطلاعات در داخل سیاهچاله ذخیره نمیشود، بلکه در سرحد آن، یعنی همان افق رویداد، ذخیره میشود. این اطلاعات در افق رویداد به یک هولوگرام دو بعدی بدل میشود (پدیدهای که به ابربرگردان (super translation) موسوم است). هاوکینگ گفت: "ایده ما این است که ابربرگردانها، هولوگرام ذرات وارد شونده هستند؛ بنابراین، شامل همه اطلاعاتی هستند که در غیر این صورت از میان خواهد رفت."[۷۲]
بر اساس نظریه نسبیت عام اینشتین، که میگوید این اطلاعات باید نابود شود و به معما یا پارادوکس اطلاعات سیاهچاله معروف است مادهای به درون سیاهچاله بلعیده میشود، و در آن سوی افق رویداد میافتد.
هولوگرام ظاهراً نشان میدهد که تصویر اینشتین از سیاهچاله درست نیست. به ویژه اینکه، اصلاً معلوم نیست که سیاهچالهها دارای 'بخش درونی' باشند (مادهای که مکیده میشود ممکن است در افق رویداد گیر کند و به عنوان هولوگرام آنجا حفظ شود).[۷۳]
شکلگیری و تکامل[ویرایش]
با در نظر گرفتن ماهیت عجیب سیاهچالهها شاید طبیعی باشد، که این سؤال به ذهن خطور کند که آیا چنین اجسام عجیبی میتوانند در طبیعت وجود داشته باشند، یا اینکه این اجسام تنها جوابهای پاتولوژیکی برای معادلات انیشتین هستند. خود انیشتین به اشتباه گمان میکرد که سیاهچالهها نمیتوانند تشکیل شوند زیرا او بر این باور بود که تکانه زاویهای ذرات در حال سقوط حرکت آنها را در شعاع خاصی پایدار مینمود.[۷۴] این باعث شد که جامعه نسبیت عام تا مدتها نتایج مخالف را از دست بدهد.[۷۵] هر چند که گروه کمتری از نسبیت پردازان همچنان بر این باور بودند که سیاهچالهها اجسام فیزیکی واقعی هستند[۷۶] و این گروه تا پایان دهه ۱۹۶۰ اکثر پژوهشگران این زمینه را متقاعد کرده بودند که هیچ مانعی برای بهوجود آمدن افق رویداد وجود ندارد.
زمانی که یک افق رویداد تشکیل میشود، پنروز ثابت نمود که یک تکینگی در نقطهای درون آن بهوجود میآید.[۷۷] مدت کوتاهی پس از وی هاوکینگ نشان داد که بسیاری از راه حلهای کیهانشناسی که مهبانگ را توصیف میکنند نقاط تکینهای بدون میدانهای اسکالر یا مواد عجیب دیگر دارند. راه حل سیاهچاله کر، نظریه بدون مو و قوانین ترمودینامیک سیاهچالهها نشان دادند که خواص فیزیکی سیاهچالهها ساده و قابل فهم هستند و این اجسام موضوعات مناسبی برای پژوهش هستند. ابتداییترین فرایندی که انتظار میرود به تشکیل سیاهچالهها بینجامد، رمبش گرانشی اجسام بسیار سنگین همچون ستاره هاست. البته فرایندهای عجیب تری نیز هستند که ممکن است به تولید سیاهچالهها بینجامد.[۷۷]
رمبش گرانشی[ویرایش]
رمبش گرانشی زمانی رخ میدهد که فشار داخلی یک جسم برای مقاومت در برابر نیروی گرانشی خود جسم کافی نباشد. برای ستارگان این حادثه زمانی اتفاق میافتد که یا به دلیل کم شدن سوخت ستاره برای تولید انرژی از طریق سنتزهای هستهای قادر به حفظ دمای خود نباشد یا اینکه یک ستاره پایدار ماده اضافهای دریافت کند به گونهای که دمای هسته آن بالاتر نرود. در هردوی این موارد دمای ستاره به اندازه کافی زیاد نخواهد بود که از فروپاشی آن زیر وزن خودش جلوگیری کند (قانون گازهای ایدهآل ارتباط بین فشار، دما و حجم را توضیح میدهد).[۷۸]
این رمبش ممکن است بر اثر فشار تباهیدگی اجزای تشکیل دهنده ستاره متوقف گردد و باعث فشرده شدن ماده به مادهای که به اندازه شگفتانگیزی چگال تر است بشود. حاصل این اتفاق یکی از انواع ستارگان فشرده است که نوع ستاره فشرده به وجود آمده به جرم ماده باقیمانده بستگی دارد. ستاره در هنگام تغییرات نشات گرفته از رمبش گرانشی (مانند یک ابرنواختر یا سحابی سیارهنما) بخش قابل توجهی از جرم خود را از لایههای خارجی به فضای اطراف پرتاب میکند. اگر جرم مواد باقیمانده ۵درصد جرم خورشیدی باشد جرم ستاره اولیه پیش از فروپاشی احتمالاً بیش از ۲۰ جرم خورشیدی بودهاست.[۷۸]
اگر جرم مواد باقیمانده بیش از ۳ الی ۴ برابر جرم خورشید باشد (حد تولمن-اوپنهایمر-وولکوف) - چه به دلیل سنگین بودن ستاره اصلی چه به دلیل اینکه ماده باقیمانده جرم اضافهای را از طریق تجمع ماده گردآوری کرده باشد - حتی فشار تباهیدگی نوترونها برای متوقفسازی فروپاشی کافی نخواهد بود. پس از این هیچ مکانیزم شناخته شدهای (شاید به جز تباهیدگی کوارکها در ستارههای کوارکی) قدرت کافی برای متوقفسازی فروپاشی را ندارد و جسم ناگریز به یک سیاهچاله فروپاشیده میشود.[۷۸]
گمان میرود که این رمبش گرانشی ستارگان سنگین عامل پیدایش سیاهچالههای ستاره وار است. ستارهزایی در جهان جوان احتمالاً به ایجاد ستارگانی بسیار سنگین انجامیدهاست که در هنگام رمبش سیاهچالههایی تا هزار برابر جرم خورشید بهوجود آوردهاند. این سیاهچاله میتوانند بذرهایی برای سیاهچالههای کلان جرمی بوده باشند که امروزه در مرکز بسیاری از کهکشانها یافت میشوند.[۷۹]
درحالیکه بیشتر انرژی آزاد شده در خلال یک رمبش گرانشی به سرعت پخش میشود یک ناظر خارجی در واقع پایان این فرایند را نمیبیند. اگرچه این رمبش در چارچوب مرجع ماده در حال فروپاشی در زمان محدودی صورت میگیرد اما برای یک ناظر دور ماده در حال فروپاشی کندتر میشود و در بالای افق رویداد متوقف میشود. دلیل این پدیده اتساع زمان گرانشی است. برای نور بیشتر و بیشتر طول میکشد تا از ماده در حال رمبش به ناظر برسد؛ و نوری که درست قبل از تشکیل افق رویداد منتشر میشود با تأخیر بینهایت به ناظر میرسد. از این رو ناظر خارجی هرگز تشکیل افق رویداد را نخواهد دید؛ در عوض ماده در حال رمبش تاریک تر. تاریک تر میشود و انتقال به سرخ رو به افزایشی خواند داشت و سرانجام کاملاً محو میشود.[۸۰]
سیاهچالههای نخستین در مهبانگ[ویرایش]
رمبش گرانشی نیاز به چگالی بالا دارد. در دوره کنونی جهان، چگالیهای بالا تنها در ستارگان یافت میشود. اما در جهان نخستین اندکی پس از مهبانگ چگالیها بسیار بیشتر بودند، که احتمال تشکیل سیاهچاله را فراهم مینمود. چگالی بالا به تنهایی برای بهوجود آمدن سیاهچاله کافی نیست زیرا یک توزیع جرم یکنواخت اجازه تجمع جرم را نمیدهد برای اینکه سیاهچالههای نخستین در چنین رسانه چگالی امکان پیدایش داشته باشند باید آشفتگیهای اولیهای در چگالی بهوجود آمده باشند که بتوانند پس از آن تحت گرانش خودشان رشد کنند. مدلهای مختلف از جهان اولیه، از لحاظ اندازهای که برای این آشفتگیها پیشبینی کردهاند با هم بسیار متفاوتند. این مدلهای متفاوت جرم سیاهچالههای نخستین را از یک واحد پلانک تا صدها هزار جرم خورشیدی پیشبینی کردهاند.[۸۱] سیاهچالههای نخستین عامل پیدایش همه سیاهچالههای دیگر شمرده میشوند.
برخوردهای پرانرژی[ویرایش]
رمبش گرانشی تنها فرایندی نیست که سیاهچاله را بهوجود میآورد. در اصل سیاهچالهها میتوانند از برخوردهای پرانرژی که چگالی کافی ایجاد میکنند نیز بهوجود آیند؛ اما تا به امروز ردی از چنین رویدادی چه به صورت مستقیم و چه به صورت غیر مستقیم از روی کسری در موازنه جرم در آزمایشهای شتابدهنده ذرات، کشف نشدهاست.[۸۲] این واقعیت پیشنهاد میکند که باید حد پایینی برای جرم سیاهچالهها وجود داشته باشد. از لحاظ نظری این حد باید پیرامون جرم پلانک باشد که در آن انتظار میرود که تأثیرات کوانتومی باعث شکست تئوری نسبیت عام بشوند.[۸۳] این امر سبب میشود که ایجاد سیاهچالهها از دسترس هر برخورد پر انرژی که در روی زمین یا نزدیک به آن رخ میدهد، دور باشد. اما برخی از توسعههای اخیر در گرانش کوانتومی پیشنهاد میدهند که جرم پلانک ممکن است بسیار کمتر از این باشد؛ مثلاً برخی از سناریوهای جهان غشایی مقداری بسیار کمتر برای این ثابت در نظر میگیرند.[۸۴] این امر امکان ایجاد ریزسیاهچالهها را در برخوردهای پر انرژی مانند برخورد اشعههای کیهانی با جو زمین یا احتمالاً در برخورددهنده هادرونی بزرگ در سرن را امکانپذیر میسازد. هر چند که این نظریهها بسیار گمانی هستند و به نظر بسیاری از متخصصین تشکیل ریزسیاهچالهها در چنین برخوردهای نامحتمل میآید.[۸۵] حتی اگر ریز سیاهچالهها در اثر این برخوردها تشکیل شوند انتظار میرود که در۱۰۲۵− ثانیه تبخیر شوند و تهدیدی برای زمین بهشمار نمیآیند.[۸۶]
رشد[ویرایش]
وقتی که یک سیاهچاله تشکیل شد میتواند با جذب ماده اضافی به رشد خود ادامه دهد. هر سیاهچالهای بهطور پیوسته گاز و غبار میان ستارهای را از محیط مستقیم اطرافش و تابش زمینه کیهانی که در همه جا حضور دارد، جذب میکند. این فرایند اولیهای است که به نظر میرسد سیاهچالههای کلان جرم طی آن شکل میگیرند.[۷۹] فرایندی مشابه نیز برای تشکیل سیاهچالههای جرم متوسط در خوشههای ستارهای کروی پیشنهاد شدهاست.[۸۷]
امکان دیگر برای رشد یک سیاهچاله آمیختن با اجرام دیگر مانند ستارگان یا سایر سیاهچاله هاست. این نظریه به خصوص برای سیاهچالههای کلان جرم نخستین که منشأ پیدایش بسیاری از اجسام کوچکتر بودهاند اهمیت پیدا میکند.[۷۹] این فرایند همچنین به عنوان مبدأ پیدایش برخی از سیاهچالههای با جرم متوسط پیشنهاد شدهاست.[۸۸][۸۹]
تبخیر[ویرایش]
در سال ۱۹۷۴ هاوکینگ نشان داد که سیاهچالهها کاملاً سیاه نیستند بلکه مقدار اندکی تابش گرمایی دارند[۹۰] او این نتیجه را از بهکارگیری نظریه میدانهای کوانتومی در یک زمینهٔ سیاهچالهای ایستا به دست آورد. نتیجه این محاسبات این بود که سیاهچالهها باید ذراتی را در جسم سیاه کامل منتشر کند. این اثر به نام تابش هاوکینگ نامیده شدهاست. از زمانی که هاوکینگ این نتایج را منتشر نمود بسیاری درستی این نظریه را با روشهای مختلف سنجیدهاند.[۹۱] چنانچه این نظریه تابش سیاهچالهها درست باشد انتظار میرود که سیاهچالهها یک طیف گرمایی ساطع کنند که منجر به کاهش جرم آنها میشود. این کاهش جرم مربوط به جرم فوتونها و ذراتی است که تابیده میشوند. سیاهچالهها در طول زمان تبخیر میشوند و کوچکتر میگردند. دمای این طیف (دمای هاوکینگ) با گرانش سطحی یک سیاهچاله مرتبط است که در مورد سیاهچالههای شوارتزشیلد نسبت معکوسی با جرم دارند و در نتیجه سیاهچالههای بزرگتر تابش کمتری از سیاهچالههای کوچکتر دارند.[۹۲]
یک سیاهچاله ستاره وار با جرمی برابر یک جرم خورشیدی، دمای هاوکینگی در حدود ۱۰۰ نانو کلوین دارد.[۹۳] این دما بسیار کمتر از دمای ۲٫۷ کلوینی تابش زمینه کیهانی است. سیاهچالههای ستارهای و سیاهچالههای بزرگتر از آنها بیش از آنکه از طریق تابش هاوکینگ جرم از دست بدهند، از تابش زمینه کیهانی جرم به دست میآورند. در نتیجه به جای کوچکتر شدن رشد میکنند. برای اینکه یک سیاهچاله بتواند تبخیر شود باید دمای تابش هاوکینگ آن بیشتر از ۲٫۷ کلوین باشد و این بدان معنی است که میبایست از ماه سبکتر باشد و نتیجتاً قطری کمتر از یک دهم میلیمتر داشته باشد.[۹۴]
از سوی دیگر اگر سیاهچالهای کوچک باشد انتظار میرود که تابش آن بسیار قویتر باشد. حتی سیاهچالهای که نسبت به انسان سنگین محسوب شود باید در یک دم تبخیر شود. یک سیاهچاله با وزن یک ماشین باید در مدت چند نانوثانیه تبخیر شود و طی این مدت اندک درخششی به اندازه ۲۰۰ برابر خورشید خواهد داشت. سیاهچالههای کوچکتر حتی با سرعت بیشتری تبخیر میشوند. البته برای چنین سیاهچاله کوچکی اثرات گرانش کوانتومی نقش مهمی ایفا میکنند و ممکن است (هرچند که از دانستههای فعلی در مورد گرانش کوانتومی چنین امری محتمل به نظر نمیرسد[۹۵]) به صورت فرضی چنین سیاهچاله کوچکی را پایدار سازند.[۹۶]
طبقهبندی بر اساس جرم[ویرایش]
سیاهچالهها را عموماً بر مبنای جرمشان و مستقل از بار و تکانه زاویهای دستهبندی میکنند. بر این اساس سیاهچالهها را میتوان به چهار دسته تقسیم نمود. اندازه یک سیاهچاله که با شعاع افق رویداد (شعاع شوارتزشیلد) آن سنجیده میشود با جرم آن برپایه رابطه زیر بهطور تقریبی متناسب است:[۹۷]
این رابطه تنها در مورد سیاهچالههایی با تکانه زاویهای و بار الکتریکی صفر دقیق خواهد بود و در مورد سیاهچالههای کلی تر به صورت تقریبی و با اختلافی تا حتی دو برابر در برخی موارد، صادق است.
| دسته | جرم | اندازه |
|---|---|---|
| سیاهچالههای کلان جرم | ~۱۰۵–۱۰۹ MSun | ~۰٫۰۰۱–۱۰ AU |
| سیاهچالههای جرم متوسط | ~۱۰۳ MSun | ~۱۰۳ km = REarth |
| سیاهچالههای ستاره وار | ~۱۰ MSun | ~۳۰ km |
| ریزسیاهچالهها | تا~Mماه | تا ~۰٫۱ mm |
سیاه چالههای کلان جرم[ویرایش]
جرمی بین چندمیلیون تا چند میلیارد برابر جرم خورشید دارند و پیشبینی میشود که در مرکز همه کهکشانها از جمله کهکشان راه شیری وجود داشته باشند.[۹۸][۹۹]
کهکشان نزدیک زن برزنجیر در فاصله ۲٫۵ میلیون سال نوری سیاهچاله مرکزی به جرم ۱۰۸×(۲٫۳–۱٫۱) جرم خورشیدی دارد که از سیاهچاله کهکشان راه شیری بزرگتر است.[۱۰۰] به نظر میرسد که بزرگترین سیاهچاله کلان جرم در نزدیکی راه شیری سیاهچاله مرکزی کهکشان مسیه ۸۷ است که جرمی برابر با ۱۰۹×(۰٫۵±۶٫۴) جرم خورشیدی دارد که به فاصله ۵۳٫۵ میلیون سال نوری از ما قرار گرفتهاست.[۱۰۱][۱۰۲] بزرگترین سیاهچاله شناخته شده تا تاریخ نوامبر ۲۰۰۸، سیاه چاله OJ 287 در صورت فلکی خرچنگ است که در فاصله ۳٫۵ میلیارد سال نوری واقع شدهاست و جرم آن ۱۸ میلیارد برابر جرم خورشید است.[۱۰۳]
سیاهچالههای جرم متوسط[ویرایش]
شکاف بین جرم سیاهچالههای معمولی و سیاهچالههای کلان جرم، اخترشناسان را بر آن داشت که به جستجوی سیاهچالههایی با جرم صد تا صد هزار برابر جرم خورشید برآیند. یکی از روشهای مشاهدهٔ اینگونه سیاهچالهها یافتن منابع اشعه با شدت زیاد است. منابع فوق درخشان پرتو ایکس در کهکشانهای نزدیک ممکن است سیاهچاله جرم متوسط باشند.[۱۰۴][۱۰۵] این منابع فوق درخشان پرتو ایکس در نواحی شکلگیری ستارهها (مانند مسیه ۸۲) مشاهده شدهاست و به نظر میرسد که با خوشههای ستارهای جوانی که در آن نواحی یافت میشوند مرتبطاند. روش دیگر تشخیص آنها ممکن است مشاهده تابش گرانشی منتشر شده از جسم فشرده باقیماندهای است که به دور سیاهچاله جرم متوسط میگردد.[۱۰۶] رابطهام-سیگما نیز وجود سیاهچالههایی به اندازه ۱۰۴ تا ۱۰۶ جرم خورشیدی را در کهکشانهای کم نور پیشبینی میکند. هیچ راه مستقیمی برای شکلگیری آنان شناخته نشدهاست اما گمان میرود این نوع از برخورد سیاهچالههای با جرم کمتر شکل میگیرد. نطریه دیگری نیز آنها را سیاهچالههای نخستینی میداند که در مه بانگ شکل گرفتهاند. نطریه سومی نیز آنها را حاصل از برخورد ستارگان بزرگ در خوشههای ستارهای متراکم میدانند که حاصل این برخورد به یک سیاهچاله میان جرم رمبش میکند.
سیاهچالههای ستارهوار[ویرایش]
این سیاهچالهها از رمبش گرانشی ستارههای بزرگ بهوجود میآیند.[۱۰۷] این سیاهچالهها جرمی بین سه تا چند ده برابر جرم خورشید دارند.[۱۰۸] بهترین نامزدهای احتمالی برای این دسته از سیاهچالهها، منظومههای دوتایی گسیلکننده اشعه X هستند که در اوایل دهه هفتاد مورد توجه قرار گرفتند. یکی از دو جسم در این منظومهها قابل مشاهده نیست که نامزد سیاهچاله بودن است. ماده از ستاره ندیم به سیاهچاله میریزد و پرتو ایکس تابش میکند.[۱۰۹][۱۱۰][۱۱۱]
نمونهای از این منظومههای دو تایی، ماکیان ایکس یک(Cygnus X-1) است که از یک ستاره ابرغول آبی با جرمی در حدود بیست برابر جرم خورشید و یک ندیم نامرئی با جرم تقریبی چهل برابر جرم خورشید است. در این سیستم دوتایی، جرم از ستاره قابل رویت دوتایی به درون سیاهچاله وارد میشود ولی به دلیل سرعت زاویهای، این جرم به صورت شعاعی وارد سیاهچاله نشده بلکه گازها تشکیل یک دیسک داده که قرص برافزایشی نامیده میشود.
ریزسیاهچالهها[ویرایش]
این سیاهچالهها سیاهچالههای بسیار کوچکی هستند. جرم این سیاهچالهها به اندازهای کوچک است است که در آنها اثرات مکانیک کوانتومی اهمیت زیادی پیدا میکند و از این رو به نام سیاهچالههای مکانیک کوانتومی نیز شناخته میشوند.[۱۱۲] محاسبات هاوکینگ نشان میدهد که هرچه سیاهچاله کوچکتر باشد سرعت تبخیر آن بیشتر است و در نتیجه ریزسیاهچالهها در صورت بهوجود آمدن احتمالاً در لحظهای تبخیر شده و منفجر میگردند.[۱۱۳]
شواهد تجربی[ویرایش]
سیاهچالهها به خودی خود هیچ سیگنالی به جز تابش فرضی هاوکینگ از خود منتشر نمیکنند و از آنجاییکه این تابش در مورد یک سیاهچاله اختر فیزیکی بسیار ضعیف است هیچ راهی وجود ندارد که بتوان مستقیماً از روی زمین سیاهچالههای اختر فیزیکی را ردیابی نمود. تنها استثنایی که ممکن است تابش هاوکینگ ضعیفی نداشته باشد، آخرین مرحله تبخیر سیاهچالههای کم جرم نخستین است. جستجو برای یافتن چنین تابشهایی در گذشته ناموفق بودهاست و این موضوع محدودیتهایی بر امکان وجود سیاهچالههای نخستین با جرم کم وارد میکند.[۱۱۴] تلسکوپ فضایی پرتوی گامای فرمی ناسا که در سال ۲۰۰۸ به فضا فرستاده شد به جستجو برای وجود این نشانهها ادامه خواهد داد.[۱۱۵]

از این رو اختر فیزیکدانان برای جستجوی سیاهچالهها باید به مشاهدات غیر مستقیم روی آورند. وجود یک سیاهچاله را گاهی میتوان از برهمکنشهای گرانشی آن با محیط اطرافش استنباط نمود.
بر افزایش ماده[ویرایش]
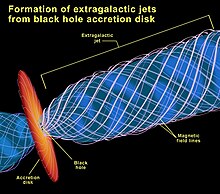
قرص برافزایشی بسیار داغ و چرخان پیرامون یک سیاهچاله که متشکل از مواد در حال سقوط به درون میباشد، آشکارترین نشانه برای شناسایی سیاهچالهها است. به خاطر حفظ تکانه زاویهای گازهایی که به چاه گرانشی یک جسم پرجرم سقوط میکنند ساختاری قرص مانند در اطراف جسم ایجاد میکنند. اصطکاک درون قرص سبب میشود تا تکانه زاویهای به سوی بیرون منتقل شود و ماده بیشتر به سمت داخل سقوط میکند و انرژی پتانسیلی آزاد میکند که دمای گاز را افزایش میدهد.[۱۱۷] در مورد اجرام فشرده همچون کوتولههای سفید، ستارههای نوترونی و سیاهچالهها، گاز در نواحی داخلی به اندازهای داغ میشود که تابش بسیاری (عمدتاً پرتو ایکس) از خود گسیل میکند که توسط تلسکوپها قابل ردیابی است. این فرایند برافزایش یکی از کاراترین فرایندهای تولید انرژی است که تا کنون شناخته شدهاست. تا ۴۰٪ باقیمانده ماده برافزوده ممکن است از طریق تابش منتشر شود[۱۱۷](در یک همجوشی هستهای تنها ۰٬۷٪ از باقی جرم به صورت انرژی منتشر میشود). در بسیاری از موارد این قرص با فوارههای نسبیتی همراه است که در امتداد قطبها منتشر میشوند و انرژی بسیاری در خود دارند. مکانیزم تشکیل این فوارهها هنوز به درستی فهمیده نشدهاست.
بسیاری از پدیدههای پرانرژی تر در جهان به برافزایش ماده در سیاهچالهها نسبت داده میشود. بهطور خاص، هسته کهکشانی فعال و اختروشها گمان میشود که قرصهای بر افزایشی سیاهچالههای کلان جرم باشند. به همین ترتیب گمان میرود که دوتاییهای پرتو ایکس منظومههای دوتایی هستند که یکی از این دو ستاره جسمی فشردهاست که ماده را از ستاره ندیم برافزایش میکند. همچنین پیشنهاد شدهاست که برخی از منابع فوق درخشان پرتو ایکس ممکن است قرصهای برافزایشی سیاهچالههای جرم متوسط باشند.[۱۱۸]
دوتاییهای پرتو ایکس[ویرایش]
دوتاییهای پرتو ایکس یا ستارههای دوتایی که در قسمت پرتو ایکس طیف، روشن هستند. این تابشهای پرتو ایکس گمان میرود که توسط یکی از ستارهها ایجاد میشود که جسمی فشردهاست و ماده را از ستاره معمولی همراهش برافزایش میکند. حضور یک ستاره معمولی در این منظومههای دوتایی موقعیتی منحصربهفرد برای مطالعه جسم دیگر و بررسی سیاهچاله بودن آن در اختیار میگذارد.

اگر چنین منظومهای سیگنالهایی منتشر کند که رد آن مستقیماً به جسم فشرده برسد، این جسم نمیتواند سیاهچاله باشد؛ هرچند که نبودن این سیگنال نیز احتمال ستاره نوترونی بودن جسم فشرده را ازبین نمیبرد. با مطالعه ستاره ندیم (همراه) اغلب میتوان پارامترهای مداری منظومه را بهدست آورده و تخمینی برای جرم جسم فشرده ارائه کرد. اگر این جرم به میزان قابل توجهی از حد تولمن-اوپنهایمر-وولکوف (که در واقع بیشینه جرم ممکن برای یک ستاره نوترونی پیش از رمبش است) بیشتر باشد، دیگر این جسم نمیتواند ستاره نوترونی باشد و پندار عمومی بر سیاهچاله بودن آن است.[۱۰۷] ماکیان ایکس-یک، اولین نامزد قوی برای سیاهچاله بودن، در سال ۱۹۷۲ به همین روش توسط چارلز توماس بولتون، لوییس وبستر و پل مردین کشف شد.[۱۱۹][۱۲۰][۱۲۱][۱۲۲] هرچند که تردیدهایی در مورد سیاهچاله بودن آن وجود دارد زیرا ستاره ندیم از ستارهای که نامزد سیاهچاله بودن است بسیار سنگین تر است.[۱۰۷] اکنون نامزدهای بهتری برای سیاهچاله بودن در رده دوتاییهای پرتو ایکس شناخته شدهاند که متغیرهای پرتو ایکس نرم نامیده میشوند.[۱۰۷] در این منظومهها ستاره ندیم نسبتاً کم جرم است و اجازه تخمین دقیقتری برای جرم سیاهچاله میدهد. افزون بر این، این منظومهها تنها چند ماه در هر ۱۰ تا ۵۰ سال منبع فعال پرتو ایکس هستند. در طول دوره تابش کم پرتو ایکس (دوره خاموشی)، قرص برافزایشی کم نور است و امکان مشاهده جزئیات ستاره ندیم در این دوره را فراهم میسازد. یکی از بهترین این دسته از نامزدها سیگنی وی-۴۰۴ (V404 Cygni) است.
نوسانهای نیمه متناوب[ویرایش]
انتشار پرتو ایکس از قرصهای برافزایشی در بسامدهای مشخصی دچار سوسو زدن میشود. این سیگنالها را نوسانهای نیمه متناوب مینامند. گمان میرود که این سیگنالها ناشی از حرکت ماده در لبه داخلی قرص برافزایشی باشند (درونیترین مدار دایرهای پایدار) و به همین دلیل با جرم جسم فشرده مرتبطاند. از این رو گاهی به عنوان راه جایگزینی برای تعیین جرم سیاهچالههای احتمالی به کار میروند.[۱۲۳]
هسته کهکشانی[ویرایش]

اخترشناسان برای توصیف کهکشانهایی که ویژگیهای غیرمعمولی مانند خط طیفی غیرمعمولی یا تابشهای رادیویی بسیار قوی دارند، از واژه کهکشان فعال استفاده میکنند. مطالعات نظری و تجربی نشان دادهاند که فعالیت این هستههای کهکشانی فعال(AGN) را میتوان با استفاده از سیاهچالههای کلان جرم توضیح داد. این گونه مدلهای هستههای کهکشانی فعال از یک سیاهچاله کلانجرم، یک قرص برافزایشی و دو فواره عمود بر قرص برافزایشی تشکیل میشوند.[۱۲۴][۱۲۵]
اگرچه انتظار میرود که سیاهچالههای کلان جرم در مرکز همه هستههای کهکشانی فعال حضور داشته باشند؛ اما تنها برخی از هستههای کهکشانی مورد مطالعه دقیق برای شناسایی و اندازهگیری جرم واقعی این نامزدهای سیاهچاله کلان جرم، قرار گرفتهاند. برخی از مهمترین کهکشانها با نامزدهایی برای سیاهچاله کلان جرم عبارتند از: کهکشان زن برزنجیر، مسیه ۳۲، مسیه ۸۷، انجیسی ۳۱۱۵، انجیسی ۳۳۷۷، نجیسی ۴۲۵۸ و کهکشان کلاهمکزیکی.[۱۲۶]
امروزه به گستردگی پذیرفته شدهاست که در مرکز همه (تقریباً) کهکشانها (نه تنها کهکشانهای فعال) یک سیاهچاله کلان جرم قرار گرفتهاست.[۹۸] همبستگی تجربی نزدیک بین جرم این چاله و پراکندگی سرعت در بخش برآمده خود کهکشان که به رابطهام-سیگما (M-Sigma)معروف است، قویا پیشنهاد میکند که ارتباطی بین شکلگیری سیاهچاله و شکلگیری خود کهکشان وجود دارد.[۱۲۷]
در حال حاضر بهترین گواه برای یک سیاهچاله کلان جرم از مطالعه حرکات خاص ستارگان در نزدیکی مرکز کهکشان راه شیری خودمان به دست میآید.[۱۲۸] از سال ۱۹۹۵ اختر شناسان حرکت ۹۰ ستاره را در ناحیهای به نام کمان ای* ردیابی نمودهاند. با تطبیق حرکت این ستارگان بر مدارهای کپلری در سال ۱۹۹۸ به این نتیجه رسیدند که باید جرمی برابر ۲٫۶ میلیون جرم خورشیدی در حجمی به شعاع ۰٫۲ سال نوری قرار گرفته باشند.[۱۲۹] از آن زمان تا کنون یکی از این ستارگان - به نام اس-۲ - یک مدار کامل را پیمودهاست. آنها موفق شدند از روی دادههای مداری، محدودیتهای مناسبتری برای جرم و اندازه این شی- که باعث حرکت مداری ستارگان ناحیه کمان ای* میشود- وضع کنند. آنها دریافتند که یک جرم کروی برابر ۴٫۳ میلیون جرم خورشیدی در ناحیهای به شعاع ۰٫۰۰۲ سال نوری قرار گرفتهاست.[۱۲۸] اگرچه این شعاع تقریباً ۳۰۰۰ برابر شعاع شوارتزشیلد متناظر با این جرم است، اما دست کم با این حقیقت که جسم مرکزی یک سیاهچاله کلان جرم باشد سازگار است.[۱۲۹]
همگرایی گرانشی[ویرایش]

تغییر شکل فضا زمان در اطراف یک جسم سنگین سبب میشود که پرتوهای نور شبیه به آنچه که در یک عدسی نوری رخ میدهد، همگرا شوند. این پدیده به نام همگرایی گرانشی خوانده میشود. مشاهداتی از یک همگرایی گرانشی بسیار ضعیف صورت گرفتهاست که فوتونها را تنها به اندازه چند ثانیه قوسی خم میکند. هرچند که این پدیده هرگز مستقیماً برای یک سیاهچاله مشاهده نشدهاست.[۱۳۰] یک راه ممکن برای مشاهده همگرایی گرانشی توسط یک سیاهچاله میتواند مشاهده ستارهها در مدار پیرامون سیاهچاله باشد. چندین نامزد مختلف برای چنین مشاهداتی در ناحیه کمان-ای وجود دارند.[۱۳۰]
امواج گرانشی[ویرایش]
یکی از راههای کشف سیاهچالهها استفاده از امواج گرانشی است که هنگام فروپاشی گسیل میدارند. هر جرم اختری از دید شکل نامتقارن تشعشع ممکن است یک منبع قابل اکتشاف مشخص به وجود آورد. جوزف وبر از دانشگاه مریلند، پیشکسوت رشته تشعشع گرانشی، رویدادهای زیادی را کشف کردهاست که نمایانگر ویرانی وسیع ماده در جهان، از راه فروپاشی گرانشی است. کارافزار او عبارت است از آنتنهای آلومینیومی، ابزاری که بهوسیله سیمهایی در داخل اتاقهای حفاظداری آویزانند. این کارافزار او قادر به کشف سیاهچالهاست، اما این کار را نمیتواند به دقت انجام دهد.[۱۳۱]
امکانهای دیگر[ویرایش]
شاهد تجربی سیاهچالههای ستارهای بر این قانون استوار است که حد بالایی برای جرم یک ستاره نوترونی وجود دارد. اندازه این حد نیز به میزان زیادی به فرضیاتی که در مورد خواص یک ماده چگال در نظر گرفته شدهاند بستگی دارد. فازهای جدید و عجیب ماده ممکن است این حد را بالاتر ببرند.[۱۰۷] فازی از ماده که دارای کوارکهای آزاد با چگالی بالا ممکن است اجازه وجود ستارههای کوارکی چگال را بدهد[۱۳۲] و برخی مدلهای ابرتقارنی نیز وجود ستارگان کیو را پیشبینی میکنند.[۱۳۳] برخی از گسترشهای مدل استاندارد ادعای وجود ذراتی به نام پرئون را دارند که از اجزای بنیادی سازنده کوارکها و لپتونها هستند که بهطور فرضی ممکن است تشکیل ستارههای پرئونی را بدهند.[۱۳۴] این مدلهای فرضی پتانسیل آن را دارند که گروهی از مشاهدات مربوط به نامزدهای سیاهچالههای ستارهای را توضیح دهند، هرچند که گفتگوهای همگانی نسبیت عام نشان میدهد که هر گونهای از این ستارههای فرضی نیز جرم بیشینهای خواهند داشت.[۱۰۷]
ازآنجا که چگالی متوسط یک سیاهچاله در درون شعاع شوارتزشیلدش با مربع جرم آن نسبت معکوس دارد. چگالی سیاهچالههای کلان جرم بسیار کمتر از چگالی سیاهچالههای ستارهای است (چگالی متوسط سیاهچالهای به جرم ۱۰۸ جرم خورشیدی با چگالی آب قابل مقایسهاست). پس از این فیزیک ماده تشکیل دهنده یک سیاهچاله کلان جرم بسیار بهتر فهمیده شدهاست و گاهی از مدلهای جایگزینی برای توضیح مشاهدات مربوط به سیاهچالههای کلان جرم استفاده میشود که دنیوی تر هستند. برای نمونه میتوان یک سیاهچاله کلان جرم را به عنوان دستهای از اجسام بسیار تاریک در نظر گرفت هرچند که این گونه مدلهای توضیحی جایگزینی به اندازه کافی استوار نیستند که بتوانند نامزدهای سیاهچالههای کلان جرم را توضیح دهند.[۱۰۷]
شواهد موجود در مورد سیاهچالههای ستارهای و کلان جرم نشانگر آن هستند که برای اینکه سیاهچالهها تشکیل نشوند، باید تئوری نسبیت عام به عنوان یک تئوری گرانش شکست بخورد. شاید این شکست در مقابل هجوم اصلاحات مکانیک کوانتومی باشد. یکی از ویژگیهای پیشبینی شده در مورد یک تئوری گرانش کوانتومی این است که نقطه تکینگی نخواهد داشت (و در نتیجه سیاهچالهای وجود نخواهد داشت).[۱۳۵] در سالهای اخیر مدل فازبال در نظریه ریسمان بیشترین توجه را به خود جلب نمودهاست. برپایه محاسبات انجام شده در شرایط بهخصوص در نظریه ریسمان این گونه پیشنهاد میشود که وضعیتهای منفرد یک سیاهچاله، افق رویداد یا تکینگی ندارند اما برای یک ناظر کلاسیک/نیمه کلاسیک، میانگین آماری این وضعیتهای منفرد همچون سیاهچالهای معمولی در نسبیت عام به نظر میرسد.[۱۳۶]
پرسشهای باز[ویرایش]
آنتروپی و ترمودینامیک[ویرایش]

در سال ۱۹۷۱ هاوکینگ نشان داد که در شرایط عمومی[Note ۱] مساحت کل افقهای رویداد هر مجموعهای از سیاهچالهها هرگز نمیتواند کاهش یابد حتی اگر با یکدیگر برخورد و در هم ادغام شوند.[۱۳۷] این نتیجه که امروزه به عنوان قانون دوم مکانیک سیاهچالهها شناخته میشود شباهت قابل توجهی با قانون دوم ترمودینامیک دارد که بیان میکند که آنتروپی کل سیستم هرگز کاهش نمییابد. تصور میشد که سیاهچالهها هم همچون اجسام کلاسیکی که در دمای صفر مطلق هستند، آنتروپی صفر دارند. پذیرش این تصور سبب نقض قانون دوم ترمودینامیک میشود زیرا با ورود ماده دارای آنتروپی به سیاهچاله بدون آنتروپی، آنتروپی کل در جهان به اندازه آنتروپی مادهای که جذب سیاهچاله شده کاهش مییابد. از این رو بکنشتین پیشنهاد داد که یک سیاهچاله باید آنتروپی داشته باشد و آنتروپی آن با مساحت افق رویدادش متناسب است.[۱۳۸]
پیوند با قوانین ترمودینامیک وقتی قویتر شد که هاوکینگ کشف کرد که طبق نظریه میدانهای کوانتومی یک سیاهچاله باید تابش جسم سیاه در دمای ثابت را گسیل کند. به نظر میرسد که این به معنای نقض قانون دوم مکانیک سیاهچالهها باشد زیرا این تابش انرژی را از سیاهچاله میگیرد و باعث انقباض آن میشود. هرچند که این تابش مقداری از آنتروپی را نیز به بیرون منتقل میکند و زیر شرایط کلی میتوان اثبات نمود که مجموع آنتروپی مادهای که سیاهچاله و یک چارم افق رویداد آن را فراگرفتهاست دائماً رو به افزایش است. این موضوع اجازه فرمولبندی قانون اول مکانیک سیاهچالهها را میدهد که همسنگ قانون اول ترمودینامیک است با این تفاوت که به جای انرژی، جرم؛ به جای دما، گرانش سطحی و به جای آنتروپی، مساحت قرار میگیرد.[۱۳۸]
یکی از ویژگیهای گیجکننده این است که آنتروپی یک سیاهچاله با مساحت آن تغییر میکند تا حجم آن، حال آنکه آنتروپی کمیتی وابسته به حجم است که به صورت خطی با تغییر حجم تغییر میکند. این ویژگی عجیب، جرارد توفت و لئونارد ساسکیند را بر آن داشت تا اصل هولوگرافیک را ارائه دهند که پیشنهاد میکند که هر چیزی که درون حجمی از فضا-زمان رخ میدهد را میتوان با دادههای روی مرز آن حجم توصیف نمود.[۱۳۹]
اگرچه میتوان از نسبیت عام برای محاسباتی نیمه کلاسیک آنتروپی سیاهچالهها استفاده نمود، اما این شرایط از لحاظ نظری رضایت بخش نیست. در مکانیک آماری آنتروپی عبارت است از شمار پیکربندهای میکروسکوپیک یک سیستم که خواص میکروسکوپیک یکسانی (مانند جرم، بار، دما و…) دارند. بدون یک نظریه قابل قبول برای گرانش کوانتومی انجام چنین محاسباتی برای سیاهچالهها امکانپذیر نیست. پیشرفتهایی در برخی دیدگاهها نسبت به گرانش کوانتومی صورت گرفتهاست. در سال ۱۹۹۵ اندرو اشترومینگر و کامران وفا نشان دادند که با شمارش تعداد حالات کوانتومی یک سیاهچاله ابرمتقارن در نظریه ریسمان میتوان فرمول آنتروپی هاوکینگ-بکنشتین را دوباره به دست آورد.[۱۴۰] از آن زمان تا کنون نتایج مشابهی برای سیاهچالههای متفاوت هم در نظریه ریسمان و هم در سایر دیدگاهها به گرانش کوانتومی (مانند گرانش کوانتومی حلقه) گزارش شدهاند.[۱۴۱]
یگانگی سیاهچالهها[ویرایش]
یکی از پرسشهای باز در فیزیک پایه، پارادوکس اطلاعات گمشده یا پارادوکس یگانگی سیاهچالهاست. بهطور کلاسیک قوانین فیزیک در هر دو جهت مستقیم و معکوس یکسان عمل میکنند. نظریه لیوویل (هامیلتونی) نگهداری حجم فضای فاز را - که میتوان از آن به نگهداری اطلاعات تعبیر نمود - ضروری میداند، در نتیجه حتی در فیزیک کلاسیک هم مشکلاتی وجود دارد. در مکانیک کوانتومی این مسئله متناظر با یکی از خواص اساسی به نام یگانگی است که با نگهداری احتمالات مرتبط است. آن را میتوان به عنوان نگهداری حجم فضای فاز کوانتومی، همانگونه که در ماتریس چگالی توصیف میشوند نیز در نظر گرفت.[۱۴۲]
شمار سیاهچالهها در جهان[ویرایش]
شمار سیاهچالهها در جهان به قدری زیاد است که شمردن آنها امکانپذیر نیست. کهکشان راه شیری به تنهایی در حدود صد میلیارد ستاره دارد که از هر هزار ستاره تقریباً یکی به اندازهای بزرگ هست که به سیاهچاله تبدیل شود. پس کهکشان ما باید در حدود صد میلیون سیاهچاله ستارهای داشته باشد. اما تا کنون تنها یک دوجین از آنها شناسایی شدهاند. از آنجا که در محدودهای از جهان که از زمین قابل مشاهدهاست در حدود صد میلیارد کهکشان وجود دارد و سیاهچالههای کلان جرم نیز در مرکز این کهکشانها قرار دارند پس باید در حدود صد میلیارد سیاهچاله کلان جرم در این ناحیه از جهان وجود داشته باشد.[۱۴۳]
نظریه جهانهای درون سیاهچالگان[ویرایش]
نیکدوم پاپلاوسکی، فیزیکدان نظری از دانشگاه ایندیانا پیشنهاد کردهاست که ممکن است جهان ما درون سیاهچالهای قرار گرفته باشد که خود آن در جهانی بزرگتر واقع شدهاست.[۱۴۴][۱۴۵][۱۴۶][۱۴۷][۱۴۸][۱۴۹][۱۵۰] نظریه پاپلاوسکی جایگزینی برای نظریه وجود تکینگی گرانشی در سیاهچاله هاست. او توضیحی نظری بر مبنای پیچش فضا زمان ارائه میدهد.[۱۵۱] پاپلاوسکی پیشنهاد میکند که اگر چگالی ماده در یک سیاهچاله به ۱۰۵۰ کیلوگرم بر متر مکعب برسد، پیچش به عنوان نیرویی به مقابله با گرانش تبدیل میشود و به جای تشکیل تکینگی برود همچون فنر فشردهای که به آن فشار وارد شدهاست باز میشود.[۱۵۲][۱۵۳] او عنوان نمودهاست که میزان بسیار بالای پیچش ممکن است دلیل انبساط کیهانی باشد.[۱۵۴]
علاوه بر این، این نظریه پیشنهاد میدهد که هر سیاهچالهای یک کرمچاله میشود که دربرگیرنده جهان در حال انبساط جدیدی است که از یک جهش بزرگ در سیاهچاله بهوجود آمدهاست؛ بنابراین سیاهچالههای مرکز کهکشانها ممکن است پلهایی به جهانهای دیگر باشند.[۱۵۵][۱۵۶][۱۵۷] بنابراین جهان خود ما نیز ممکن است درون سیاهچالهای باشد که خود در جهانی بزرگتر قرار گرفتهاست که پیش تر از این توسط راج پاتیرا مطرح شده بود.[۱۵۸]
تصورات اشتباه[ویرایش]
- سیاهچالهها برخلاف تصور نادرست ایجادشده از آنها، هر آنچه در اطراف آنهاست را به درون خود نمیمکند.[۱۵۹] برای مثال اگر خورشید با یک سیاهچاله با همین جرم جایگزین میشد، شعاع مدارهای سیارات تغییری نمیکرد.[۱۶۰] به شرطی که جرم ثابت باشد[۱۶۱]
- سیاهچاله صدا ندارد، براساس پژوهشهای نظری و عملی دانشمندان ناسا سیاهچاله صدایی ندارد اما آنها توضیح دادند که «یک خوشه کهکشانی آنقدر گاز دارد که ما صدای واقعی از آن دریافت کردهایم. برای شنیدن صدای سیاهچاله، امواج صوتی تقویت و با دادههای دیگر ترکیب شده است.» خوشه کهکشانی پرسیاوش که این صدا برای نخستین بار از آن ذخیره شده است حدود ۲۴۰ میلیون سال نوری از زمین فاصله دارد. کلیپ صوتی که ناسا منتشر کرده تنها در عرض دو روز، میلیونها بازدید کننده داشته و اکثر کاربران شبکههای اجتماعی موافق هستند که صدای سیاهچاله بسیار ترسناک است.[۱۶۲]
یادداشتها[ویرایش]
- ↑ بهطور خاص او در نظر گرفت که شرط انرژی ضعیف برای تمام مواد صادق است
منابع[ویرایش]
- ↑ Oldham, L. J.; Auger, M. W. (March 2016). "Galaxy structure from multiple tracers – II. M87 from parsec to megaparsec scales". Monthly Notices of the Royal Astronomical Society. 457 (1): 421–439. arXiv:1601.01323. Bibcode:2016MNRAS.457..421O. doi:10.1093/mnras/stv2982. S2CID 119166670.
- ↑ Overbye, Dennis (10 April 2019). "Black Hole Picture Revealed for the First Time – Astronomers at last have captured an image of the darkest entities in the cosmos – Comments". نیویورک تایمز. Retrieved 10 April 2019.
- ↑ Event Horizon Telescope (2019). "First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole". ژورنال اخترفیزیکی. 875 (1): L1. arXiv:1906.11238. Bibcode:2019ApJ...875L...1E. doi:10.3847/2041-8213/ab0ec7.
- ↑ Landau, Elizabeth (10 April 2019). "Black Hole Image Makes History". ناسا. Retrieved 10 April 2019.
- ↑ "The woman behind first black hole image". bbc.co.uk. بیبیسی نیوز. 11 April 2019.
- ↑ Robert M., Wald (1984). "Black Holes". General Relativity (به انگلیسی). The University of Chicago Press.
- ↑ Davies, P. C. W. (1978). "Thermodynamics of Black Holes" (PDF). Reports on Progress in Physics. 41 (8): 1313–1355. Bibcode:1978RPPh...41.1313D. doi:10.1088/0034-4885/41/8/004. Archived from the original (PDF) on 10 May 2013.
- ↑ Schutz, Bernard (2003-12-04). Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity (به انگلیسی). Cambridge University Press.
- ↑ Eisenstaedt, “The Early Interpretation of the Schwarzschild Solution,” in D. Howard and J. Stachel (eds), Einstein and the History of General Relativity: Einstein Studies, Vol. 1, pp. 213-234. Boston: Birkhauser, 1989.
- ↑ Letter from K Schwarzschild to A Einstein dated 22 December 1915, in "The Collected Papers of Albert Einstein", vol.8a, doc. #169, (Transcript of Schwarzschild's letter to Einstein of 22 Dec. 1915) بایگانیشده در ۲۷ سپتامبر ۲۰۱۱ توسط Wayback Machine.
- ↑ «What is a black hole?». بایگانیشده از روی نسخه اصلی در ۲۹ دسامبر ۲۰۱۱. دریافتشده در ۹ نوامبر ۲۰۱۱.
- ↑ "supermassive black holes" (به انگلیسی). www.nasa.gov. Archived from the original on 19 November 2011. Retrieved 16 November 2011.
- ↑ «How Big Are Black Holes?». بایگانیشده از روی نسخه اصلی در ۱۹ نوامبر ۲۰۱۱. دریافتشده در ۹ نوامبر ۲۰۱۱.
- ↑ «اولین عکس از یک سیاهچاله منتشر شد». بایگانیشده از روی نسخه اصلی در ۱۰ آوریل ۲۰۱۹. دریافتشده در ۱۰ آوریل ۲۰۱۹.
- ↑ Paul Sukys. Rowman & Littlefield (1999), Lifting the scientific veil: science appreciation for the nonscientist (به انگلیسی), p. 227
- ↑ "John Wheeler: 1911-2008 - physicsworld.com" (به انگلیسی). Apr 14, 2008. Archived from the original on 13 January 2010. Retrieved 2011-12-12.
- ↑ Michell, J (1784). "On the Means of Discovering the Distance, Magnitude, &c. of the Fixed Stars, in Consequence of the Diminution of the Velocity of Their Light, in Case Such a Diminution Should be Found to Take Place in any of Them, and Such Other Data Should be Procured from Observations, as Would be Farther Necessary for That Purpose". Philosophical Transactions of the Royal Society (به انگلیسی). 74 (0): 35-37. Bibcode:1784RSPT...74...35M. doi:10.1098/rstl.1784.0008. JSTOR 106576.
{{cite journal}}:|access-date=requires|url=(help) - ↑ Gillispie, C. C (2000). Pierre-Simon Laplace, 1749-1827: a life in exact science. Princeton paperbacks (به انگلیسی). Princeton University Press. p. 175.
- ↑ Israel, W (1989). "Dark stars: the evolution of an idea". In Hawking, S. W; Israel, W (eds.). Three Hundred Years of Gravitation (به انگلیسی). انتشارات دانشگاه کمبریج.
- ↑ ۲۰٫۰ ۲۰٫۱ Schwarzschild, K (1916). "Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (به آلمانی). 7: 196-189. Retrieved 2011-12-20. Schwarzschild, K (1916). "Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (به آلمانی). 18: 424–434. Retrieved 2011-12-20.
- ↑ Droste, J (1915). "On the field of a single centre in Einstein's theory of gravitation". Koninklijke Nederlandsche Akademie van Wetenschappen Proceedings (به آلمانی). 17 (3): 1011-998.
{{cite journal}}:|access-date=requires|url=(help); Check date values in:|تاریخ بازبینی=(help) - ↑ 't Hooft, G (2009). "Introduction to the Theory of Black Holes" [درآمدی بر نظریه سیاهچالهها] (PDF) (به انگلیسی). Institute for Theoretical Physics / Spinoza Insitute: 48-47. Retrieved 20/12/2011.
{{cite journal}}: Cite journal requires|journal=(help); Check date values in:|تاریخ بازبینی=(help) - ↑ Venkataraman، G. Chandrasekhar and his limit [چاندراسخار و حد او]. Universities Press. ص. ۸۹. doi:10.1119/1.12686. شابک ۸۱۷۳۷۱۰۳۵X.
- ↑ Detweiler, S (1981). "Resource letter BH-1: Black holes" (PDF). American Journal of Physics (به انگلیسی). 49 (5): 394–400. Bibcode:1981AmJPh..49..394D. doi:10.1119/1.12686. Retrieved 20/12/2011.
{{cite journal}}: Check date values in:|تاریخ بازبینی=(help) - ↑ Harpaz، A (۱۹۹۴). Stellar evolution [تکامل ستارهای]. A K Peters, Ltd. ص. ۱۰۵. شابک ۱-۵۶۸-۸۱۰۱۲-۱.
- ↑ Oppenheimer, J. R (1939). "On Massive Neutron Cores". Physical Review (به انگلیسی). 55 (4): 374–381. Bibcode:1939PhRv...55..374O. doi:10.1103/PhysRev.55.374.
{{cite journal}}:|access-date=requires|url=(help); Check date values in:|تاریخ بازبینی=(help) - ↑ Finkelstein، D. (۱۹۵۸). «Past-Future Asymmetry of the Gravitational Field of a Point Particle» [عدم تقارن گذشته-آینده میدان گرانشی یک ذره نقطهای]. Physical Review. ۱۱۰ (۴): ۹۶۵–۹۶۷. doi:10.1103/PhysRev.110.965. بیبکد:1958PhRv..110..965F.
- ↑ Kruskal، M. (۱۹۶۰). «Maximal Extension of Schwarzschild Metric» [گسترش ماکسیمال متریک شوارتزشیلد]. Physical Review. ۱۱۹ (۵): ۱۷۴۳. doi:10.1103/PhysRev.119.1743. بیبکد:1960PhRv..119.1743K.
- ↑ Hewish، A. (۱۹۷۰). «Pulsars» [تپ اخترها]. Annual Review of Astronomy and Astrophysics. ۸ (۱): ۲۶۵–۲۹۶. doi:10.1146/annurev.aa.08.090170.001405. بیبکد:1970ARA&A...8..265H.
- ↑ Hewish، A.؛ و دیگران (۱۹۶۸). «Observation of a Rapidly Pulsating Radio Source» [مشاهده یک منبع رادیوی سریعاً تپنده]. Nature (journal). ۲۱۷ (۵۱۳۰): ۷۰۹–۷۱۳. doi:10.1038/217709a0. بیبکد:1968Natur.217..709H.
- ↑ Pilkington, J. D. H.; et al. (1968), "Observations of some further Pulsed Radio Sources" [مشاهده برخی منابع رادیویی بیشتر تپیده], Nature (journal), vol. 218, p. 126–129, Bibcode:1968Natur.218..126P, doi:10.1038/218126a0
- ↑ Hawking، Stephen W. (۱۹۷۹). GenralRelativity: an Einstein centenary survey [نسبیت عام: بررسی قرنی انیشتین]. Cambridge University Press. Cambridge University Press. ص. ۴۵۴. شابک ۰-۵۲۱-۲۲۲۸۵-۰.
- ↑ Newman, E. T.; et al. (1965), "Metric of a Rotating, Charged Mass" [متریک یک جرم باردار چرخنده], Journal of Mathematical Physics, vol. 6, p. 918, Bibcode:1965JMP.....6..918N, doi:10.1063/1.1704351
- ↑ Israel، W. (۱۹۶۷). «Event Horizons in Static Vacuum Space-Times» [افقهای رویداد در فضا-زمانهای خلأ ایستا]. Physical Review. ۱۶۴ (۵): ۱۷۷۶. doi:10.1103/PhysRev.164.1776. بیبکد:1967PhRv..164.1776I.
- ↑ Carter، B. (۱۹۷۱). «Axisymmetric Black Hole Has Only Two Degrees of Freedom» [سیاهچاله نامتقارن محوری تنها دو درجه از آزادی دارد]. Physical Review Letters. ۲۶ (۶): ۳۳۱. doi:10.1103/PhysRevLett.26.331. بیبکد:1971PhRvL..26..331C.
- ↑ Carter، B. (۱۹۷۷). «The vacuum black hole uniqueness theorem and its conceivable generalisations». Proceedings of the 1st Marcel Grossmann meeting on general relativity. ص. ۲۴۳–۲۵۴.
- ↑ Robinson، D. (۱۹۷۵). «Uniqueness of the Kerr Black Hole». Physical Review Letters. ۳۴ (۱۴): ۹۰۵. doi:10.1103/PhysRevLett.34.905. بیبکد:1975PhRvL..34..905R.
- ↑ ۳۸٫۰ ۳۸٫۱ Heusler، M. (۱۹۹۸). «Stationary Black Holes: Uniqueness and Beyond» [سیاهچالههای ایستا: یکتایی و فراتر]. Living Reviews in Relativity. ۱ (۶). دریافتشده در ۲۰۱۱-۰۲-۰۸.
- ↑ (Carroll ۲۰۰۴، ص. ۲۵۳)
- ↑ Thorne، K. S.؛ Price، R. H. (۱۹۸۶). Black holes: the membrane paradigm [سیاهچالهها:پاردایم غشایی]. Yale University Press. شابک ۹۷۸۰۳۰۰۰۳۷۷۰۸.
- ↑ Anderson، Warren G. (۱۹۹۶). «The Black Hole Information Loss Problem» [مسئله گم شدن اطلاعات در سیاهچاله]. Usenet Physics FAQ. دریافتشده در ۲۴ مارس ۲۰۰۹.
- ↑ Preskill، J. (۱۹۹۴-۱۰-۲۱)، Black holes and information: A crisis in quantum physics [سیاهچالهها] (PDF)
- ↑ Seeds، Michael A.؛ Backman، Dana E. (۲۰۰۷)، Perspectives on Astronomy، Cengage Learning، ص. ۱۶۷، شابک ۰۴۹۵۱۱۳۵۲۲
- ↑ Shapiro، S. L.؛ Teukolsky، S. A. (۱۹۸۳). Black holes, white dwarfs, and neutron stars: the physics of compact objects [سیاهچالهها، کوتولههای سفید و ستارههای نوترونی: فیزیک اجسام فشرده]. John Wiley and Sons. ص. ۳۵۷. شابک ۰۴۷۱۸۷۳۱۶۰.
- ↑ Wald، R. M. (۱۹۹۷)، Gravitational Collapse and Cosmic Censorship، arXiv:gr-qc/9710068
- ↑ McClintock، J. E.؛ Shafee، R.؛ Narayan، R.؛ Remillard، R. A.؛ Davis، S. W.؛ Li، L. -X. (۲۰۰۶). «The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105». Astrophysical Journal. ۶۵۲ (۱): ۵۱۸–۵۳۹. arXiv:astro-ph/0606076. doi:10.1086/508457. بیبکد:2006ApJ...652..518M.
- ↑ (Thorne، Misner و Wheeler ۱۹۷۳، ص. ۸۴۸)
- ↑ (Wheeler ۲۰۰۷، ص. ۱۷۹)
- ↑ (Carroll ۲۰۰۴، Ch. 5.4 and 7.3)
- ↑ (Carroll ۲۰۰۴، ص. ۲۱۷)
- ↑ (Carroll ۲۰۰۴، ص. ۲۱۸)
- ↑ «Inside a black hole». Knowing the universe and its secrets. دریافتشده در ۲۰۰۹-۰۳-۲۶.
- ↑ (Carroll ۲۰۰۴، ص. ۲۲۲)
- ↑ Emparan، R.؛ Reall، H. S. (۲۰۰۸). «Black Holes in Higher Dimensions». Living Reviews in Relativity. ۱۱ (۶). arXiv:0801.3471. بیبکد:2008LRR....11....6E. دریافتشده در ۲۰۱۱-۰۲-۱۰.
- ↑ Obers، N. A. (۲۰۰۹). Papantonopoulos، Eleftherios، ویراستار. «Black Holes in Higher-Dimensional Gravity». Lecture Notes in Physics. ۷۶۹: ۲۱۱–۲۵۸. arXiv:0802.0519. doi:10.1007/978-3-540-88460-6.
- ↑ (hawking و ellis ۱۹۷۳، Ch. 9.3)
- ↑ (Carroll ۲۰۰۴، ص. ۲۰۵)
- ↑ (Carroll ۲۰۰۴، صص. ۲۶۴–۲۶۵)
- ↑ (Carroll ۲۰۰۴، ص. ۲۵۲)
- ↑ Lewis، G. F.؛ Kwan، J. (۲۰۰۷). «No Way Back: Maximizing Survival Time Below the Schwarzschild Event Horizon». Publications of the Astronomical Society of Australia. ۲۴ (۲): ۴۶–۵۲. arXiv:0705.1029. doi:10.1071/AS07012. بیبکد:2007PASA...24...46L.
- ↑ (Wheeler ۲۰۰۷، ص. ۱۸۲)
- ↑ (Carroll ۲۰۰۴، صص. 257–259 and 265–266)
- ↑ Droz، S.؛ Israel، W.؛ Morsink، S. M. (۱۹۹۶). <in>%20(chtitle)) «Black holes: the inside story». Physics World. ۹ (۱): ۳۴–۳۷. بیبکد:1996PhyW....9...34D.
- ↑ (Carroll ۲۰۰۴، ص. ۲۶۶)
- ↑ (Wald ۱۹۸۴، ص. ۲۱۲)
- ↑ Hamade، R. (۱۹۹۶). «Black Holes and Quantum Gravity». Cambridge Relativity and Cosmology. University of Cambridge. دریافتشده در ۲۰۰۹-۰۳-۲۶.
- ↑ Palmer، D. «Ask an Astrophysicist: Quantum Gravity and Black Holes». NASA. دریافتشده در ۲۰۰۹-۰۳-۲۶.
- ↑ ۶۸٫۰ ۶۸٫۱ Nitta، Daisuke؛ Chiba، Takeshi؛ Sugiyama، Naoshi (سپتامبر ۲۰۱۱). «Shadows of colliding black holes». Physical Review D. ۸۴ (۶). arXiv:1106.2425. doi:10.1103/PhysRevD.84.063008. بیبکد:2011PhRvD..84f3008N.
- ↑ Nemiroff، R. J. (۱۹۹۳). «Visual distortions near a neutron star and black hole». American Journal of Physics. ۶۱ (۷): ۶۱۹. arXiv:astro-ph/9312003. doi:10.1119/1.17224. بیبکد:1993AmJPh..61..619N.
- ↑ (Carroll ۲۰۰۴، Ch. 6.6)
- ↑ (Carroll ۲۰۰۴، Ch. 6.7)
- ↑ هاوکینگ: سیاهچالهها اطلاعات را ذخیره میکنند بایگانیشده در ۲۸ اوت ۲۰۱۵ توسط Wayback Machine بیبیسی فارسی
- ↑ http://www.ariamoons.com/?p=38630
- ↑ Einstein، A. (۱۹۳۹). «On A Stationary System With Spherical Symmetry Consisting of Many Gravitating Masses». Annals of Mathematics. ۴۰ (۴): ۹۲۲–۹۳۶. doi:10.2307/1968902.
- ↑ "Frontiers And Controversies In Astrophysics Transcript 9". Yale University. Archived from the original on 9 March 2016. Retrieved April 26, 2011.
- ↑ Kerr، R. P. (۲۰۰۹). «The Kerr and Kerr-Schild metrics». در Wiltshire، D. L.؛ Visser، M.؛ Scott، S. M. The Kerr Spacetime. Cambridge University Press. arXiv:0706.1109. شابک ۹۷۸۰۵۲۱۸۸۵۱۲۶.
- ↑ ۷۷٫۰ ۷۷٫۱ Penrose، R. (۱۹۶۵). «Gravitational Collapse and Space-Time Singularities». Physical Review Letters. ۱۴ (۳): ۵۷. doi:10.1103/PhysRevLett.14.57. بیبکد:1965PhRvL..14...57P.
- ↑ ۷۸٫۰ ۷۸٫۱ ۷۸٫۲ (Carroll ۲۰۰۴، Section 5.8)
- ↑ ۷۹٫۰ ۷۹٫۱ ۷۹٫۲ Rees، M. J.؛ Volonteri، M. (۲۰۰۷). «Massive black holes: formation and evolution». در Karas، V.؛ Matt، G. Black Holes from Stars to Galaxies—Across the Range of Masses. Cambridge University Press. ص. ۵۱–۵۸. arXiv:astro-ph/0701512. شابک ۹۷۸۰۵۲۱۸۶۳۴۷۶.
- ↑ Penrose، R. (۲۰۰۲). «"Golden Oldie": Gravitational Collapse: The Role of General Relativity». General Relativity and Gravitation. ۳۴ (۷): ۱۱۴۱. doi:10.1023/A:1016578408204. بیبکد:2002GReGr..34.1141P.
- ↑ Carr، B. J. (۲۰۰۵). «Primordial Black Holes: Do They Exist and Are They Useful?». در Suzuki، H.؛ Yokoyama، J.؛ Suto، Y.؛ Sato، K. Inflating Horizon of Particle Astrophysics and Cosmology. Universal Academy Press. arXiv:astro-ph/0511743. شابک ۴۹۴۶۴۴۳۹۴۰.
- ↑ Giddings، S. B.؛ Thomas، S. (۲۰۰۲). «High energy colliders as black hole factories: The end of short distance physics». Physical Review D. ۶۵ (۵): ۰۵۶۰۱۰. arXiv:hep-ph/0106219. doi:10.1103/PhysRevD.65.056010. بیبکد:2002PhRvD..65e6010G.
- ↑ Harada، T. (۲۰۰۶). «Is there a black hole minimum mass?». Physical Review D. ۷۴ (۸): ۰۸۴۰۰۴. arXiv:gr-qc/0609055. doi:10.1103/PhysRevD.74.084004. بیبکد:2006PhRvD..74h4004H.
- ↑ Arkani–Hamed، N.؛ Dimopoulos، S.؛ Dvali، G. (۱۹۹۸). «The hierarchy problem and new dimensions at a millimeter». Physics Letters B. ۴۲۹ (۳–۴): ۲۶۳. arXiv:hep-ph/9803315. doi:10.1016/S0370-2693(98)00466-3. بیبکد:1998PhLB..429..263A.
- ↑ LHC Safety Assessment Group. «Review of the Safety of LHC Collisions» (PDF). CERN.
- ↑ Cavaglià, M. (2010). "Particle accelerators as black hole factories?". Einstein-Online. 4: 1010. Archived from the original on 8 May 2013. Retrieved 8 May 2013.
- ↑ Vesperini، E.؛ McMillan، S. L. W.؛ D'Ercole، A.؛ و دیگران (۲۰۱۰). «Intermediate-Mass Black Holes in Early Globular Clusters». The Astrophysical Journal Letters. ۷۱۳ (۱): L۴۱–L۴۴. arXiv:1003.3470. doi:10.1088/2041-8205/713/1/L41. بیبکد:2010ApJ...713L..41V.
- ↑ Zwart، S. F. P.؛ Baumgardt، H.؛ Hut، P.؛ و دیگران (۲۰۰۴). «Formation of massive black holes through runaway collisions in dense young star clusters». Nature. ۴۲۸ (۶۹۸۴): ۷۲۴–۷۲۶. arXiv:astro-ph/0402622. doi:10.1038/nature02448. PMID 15085124. بیبکد:2004Natur.428..724P.
- ↑ O’leary, R. M.; Rasio, F. A.; Fregeau, J. M.; et al. (2006). "Binary Mergers and Growth of Black Holes in Dense Star Clusters". The Astrophysical Journal. 637 (2): 937. arXiv:astro-ph/0508224. Bibcode:2006ApJ...637..937O. doi:10.1086/498446.
- ↑ Hawking, S. W. (1974). "Black hole explosions?". Nature. ۲۴۸ (۵۴۴۳): ۳۰–۳۱. Bibcode:1974Natur.248...30H. doi:10.1038/248030a0.
- ↑ Page, D. N. (2005). "Hawking radiation and black hole thermodynamics". New Journal of Physics. ۷: ۲۰۳. arXiv:hep-th/0409024. Bibcode:2005NJPh....7..203P. doi:10.1088/1367-2630/7/1/203.
- ↑ (Carroll ۲۰۰۴، Ch. 9.6)
- ↑ "Frontiers And Controversies In Astrophysics Transcript 9". Yale University. Archived from the original on 9 March 2016. Retrieved April 26, 2011.
- ↑ "Evaporating black holes?". Einstein online. Max Planck Institute for Gravitational Physics. 2010. Archived from the original on 23 June 2012. Retrieved 12 December 2010.
- ↑ Giddings, S. B.; Mangano, M. L. (2008). "Astrophysical implications of hypothetical stable TeV-scale black holes". Physical Review D. ۷۸ (۳): ۰۳۵۰۰۹. arXiv:۰۸۰۶٫۳۳۸۱. Bibcode:2008PhRvD..78c5009G. doi:10.1103/PhysRevD.78.035009.
{{cite journal}}: Check|arxiv=value (help) - ↑ Peskin, M. E. (2008). "The end of the world at the Large Hadron Collider?". Physics. ۱: ۱۴. Bibcode:2008PhyOJ...1...14P. doi:10.1103/Physics.1.14.
- ↑ (Wald ۱۹۸۴، صص. ۱۲۴–۱۲۵)
- ↑ ۹۸٫۰ ۹۸٫۱ King, A. (2003). "Black Holes, Galaxy Formation, and the MBH-σ Relation". The Astrophysical Journal Letters. ۵۹۶ (۱): ۲۷–۲۹. arXiv:astro-ph/0308342. Bibcode:2003ApJ...596L..27K. doi:10.1086/379143.
- ↑ Richstone, D. et al. (January 13, 1997). "Massive Black Holes Dwell in Most Galaxies, According to Hubble Census". 189th Meeting of the American Astronomical Society. Archived from the original on 17 May 2009. Retrieved 2009-05-17.
- ↑ Bender, Ralf (۲۰۰۵–۰۹–۲۰). "HST STIS Spectroscopy of the Triple Nucleus of M31: Two Nested Disks in Keplerian Rotation around a Supermassive Black Hole". ژورنال اخترفیزیکی. ۶۳۱ (۱): ۲۸۰–۳۰۰. arXiv:astro-ph/0509839. Bibcode:2005ApJ...631..280B. doi:10.1086/432434.
{{cite journal}}: Check date values in:|date=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Gebhardt, Karl; Thomas, Jens (2009). "The Black Hole Mass, Stellar Mass-to-Light Ratio, and Dark Halo in M87". The Astrophysical Journal. ۷۰۰ (۲): ۱۶۹۰–۱۷۰۱. Bibcode:2009ApJ...700.1690G. doi:10.1088/0004-637X/700/2/1690.
{{cite journal}}: Unknown parameter|month=ignored (help)نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - ↑ Macchetto, F. ; Marconi, A. ; Axon, D. J.; Capetti, A. ; Sparks, W. ; Crane, P. (1997). "The Supermassive Black Hole of M87 and the Kinematics of Its Associated Gaseous Disk". Astrophysical Journal. ۴۸۹ (۲): ۵۷۹. arXiv:astro-ph/9706252. Bibcode:1997ApJ...489..579M. doi:10.1086/304823.
{{cite journal}}: Unknown parameter|month=ignored (help)نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - ↑ Shiga, David (10 January 2008). "Biggest black hole in the cosmos discovered". NewScientist.com news service. Archived from the original on 14 May 2008. Retrieved 7 November 2011.
- ↑ "Black Hole Boldly Goes Where No Black Hole Has Gone Before". ESA News. January 3, 2007. Archived from the original on 6 January 2007. Retrieved 2006–05–24.
{{cite news}}: Check date values in:|accessdate=(help) - ↑ Maccarone, T.J.; Zepf, SE; Rhode, KL; et al. (2007). "A black hole in a globular cluster". Nature. ۴۵۵ (۷۱۲۴): ۱۸۳–۱۸۵. arXiv:astro-ph/0701310. Bibcode:2007Natur.445..183M. doi:10.1038/nature05434. PMID ۱۷۲۰۳۰۶۲.
{{cite journal}}: Check|pmid=value (help); Explicit use of et al. in:|last2=(help) - ↑ Hopman, Clovis (2005). "Gravitational waves from remnants of ultraluminous X-ray sources". Mon.Not.Roy.Astron.Soc.Lett. ۳۶۳ (۱): L56–L60. arXiv:astro-ph/0506181. Bibcode:2005MNRAS.363L..56H. doi:10.1111/j.1745-3933.2005.00083.x.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ ۱۰۷٫۰ ۱۰۷٫۱ ۱۰۷٫۲ ۱۰۷٫۳ ۱۰۷٫۴ ۱۰۷٫۵ ۱۰۷٫۶ Celotti, A.; Miller, J.C.; Sciama, D.W. (1999). "Astrophysical evidence for the existence of black holes". Classical and Quantum Gravity. ۱۶ (12A): A3–A21. arXiv:astro-ph/9912186. doi:10.1088/0264-9381/16/12A/301.
- ↑ Hughes, Scott A. (2005). "Trust but verify: The case for astrophysical black holes". arXiv:hep-ph/0511217.
- ↑ J. Casares: Observational evidence for stellar mass black holes. Preprint بایگانیشده در ۵ نوامبر ۲۰۱۵ توسط Wayback Machine
- ↑ M.R. Garcia et al. : Resolved Jets and Long Period Black Hole Novae. Preprint بایگانیشده در ۵ نوامبر ۲۰۱۵ توسط Wayback Machine
- ↑ J.E. McClintock and R.A. Remillard: Black Hole Binaries. Preprint بایگانیشده در ۵ نوامبر ۲۰۱۵ توسط Wayback Machine
- ↑ B.J. Carr and S.B. Giddings, "Quantum black holes,"Scientific American 292N5 (2005) 30.
- ↑ Hawking, S. W. (1975). "Particle Creation by Black Holes". Commun. Math. Phys. ۴۳ (۳): ۱۹۹–۲۲۰. Bibcode:1975CMaPh..43..199H. doi:10.1007/BF02345020.
- ↑ Fichtel, C. E.; Bertsch, D. L.; Dingus, B. L.; et al. (1994). "Search of the energetic gamma-ray experiment telescope (EGRET) data for high-energy gamma-ray microsecond bursts". Astrophysical Journal. 434 (2): 557–559. Bibcode:1994ApJ...434..557F. doi:10.1086/174758.
- ↑ Naeye, R. "Testing Fundamental Physics". NASA. Archived from the original on 31 August 2008. Retrieved 2008–09–16.
{{cite web}}: Check date values in:|accessdate=(help) - ↑ Smith، Yvette (۲۰۲۲-۰۶-۰۲). «Huge Rings Around a Black Hole». NASA. دریافتشده در ۲۰۲۲-۰۶-۰۴.
- ↑ ۱۱۷٫۰ ۱۱۷٫۱ McClintock, J. E.; Remillard, R. A. (2006). "Black Hole Binaries". In Lewin, W.; van der Klis, M. (eds.). Compact Stellar X-ray Sources. Cambridge University Press. arXiv:astro-ph/0306213. ISBN 0-521-82659-4. section 4.1.5.
- ↑ Winter, L. M.; Mushotzky, R. F.; Reynolds, C. S. (2006). "XMM‐Newton Archival Study of the Ultraluminous X‐Ray Population in Nearby Galaxies". The Astrophysical Journal. ۶۴۹ (۲): ۷۳۰. arXiv:astro-ph/0512480. Bibcode:2006ApJ...649..730W. doi:10.1086/506579.
- ↑ Bolton, C. T. (1972). "Identification of Cygnus X-1 with HDE 226868". Nature. ۲۳۵ (۵۳۳۶): ۲۷۱–۲۷۳. Bibcode:1972Natur.235..271B. doi:10.1038/235271b0.
- ↑ Webster, B. L.; Murdin, P. (1972). "Cygnus X-1—a Spectroscopic Binary with a Heavy Companion ?". Nature. ۲۳۵ (۵۳۳۲): ۳۷–۳۸. Bibcode:1972Natur.235...37W. doi:10.1038/235037a0.
- ↑ Rolston, B. (10 November 1997). "The First Black Hole". The bulletin. University of Toronto. Archived from the original on 2 May 2008. Retrieved 2008–03–11.
{{cite web}}: Check date values in:|accessdate=(help) - ↑ Shipman, H. L. (1 January 1975). "The implausible history of triple star models for Cygnus X-1 Evidence for a black hole". Astrophysical Letters. ۱۶ (۱): ۹–۱۲. Bibcode:1975ApL....16....9S. doi:10.1016/S0304-8853(99)00384-4.
- ↑ "NASA scientists identify smallest known black hole" (Press release). مرکز پرواز فضایی گادرد. ۲۰۰۸–۰۴–۰۱. Archived from the original on 27 December 2008. Retrieved 2009–03–14.
{{cite press release}}: Check date values in:|accessdate=و|date=(help) - ↑ Krolik, J. H. (1999). Active Galactic Nuclei. Princeton University Press. Ch. 1.2. ISBN 0-691-01151-6.
- ↑ Sparke, L. S.; Gallagher, J. S. (2000). Galaxies in the Universe: An Introduction. Cambridge University Press. Ch. 9.1. ISBN 0–521–59704–4.
{{cite book}}: Check|isbn=value: invalid character (help) - ↑ Kormendy, J.; Richstone, D. (1995). "Inward Bound—The Search For Supermassive Black Holes In Galactic Nuclei". Annual Reviews of Astronomy and Astrophysics. ۳۳ (۱): ۵۸۱–۶۲۴. Bibcode:1995ARA&A..33..581K. doi:10.1146/annurev.aa.33.090195.003053.
- ↑ Ferrarese, L.; Merritt, D. (2000). "A Fundamental Relation Between Supermassive Black Holes and their Host Galaxies". The Astrophysical Journal Letters. ۵۳۹ (۱): ۹–۱۲. arXiv:astro-ph/0006053. Bibcode:2000ApJ...539L...9F. doi:10.1086/312838.
- ↑ ۱۲۸٫۰ ۱۲۸٫۱ Gillessen, S.; Eisenhauer, F.; Trippe, S.; et al. (2009). "Monitoring Stellar Orbits around the Massive Black Hole in the Galactic Center". The Astrophysical Journal. 692 (2): 1075. arXiv:0810.4674. Bibcode:2009ApJ...692.1075G. doi:10.1088/0004-637X/692/2/1075.
- ↑ ۱۲۹٫۰ ۱۲۹٫۱ Ghez, A. M.; Klein, B. L.; Morris, M.; et al. (1998). "High Proper‐Motion Stars in the Vicinity of Sagittarius A*: Evidence for a Supermassive Black Hole at the Center of Our Galaxy". The Astrophysical Journal. 509 (2): 678. arXiv:astro-ph/9807210. Bibcode:1998ApJ...509..678G. doi:10.1086/306528.
- ↑ ۱۳۰٫۰ ۱۳۰٫۱ Bozza, Valerio (2009). "Gravitational Lensing by Black Holes". arXiv:۰۹۱۱٫۲۱۸۷.
{{cite arxiv}}:|arxiv=required (help);|class=ignored (help); Check|arxiv=value (help) - ↑ Preparata, Giuliano (1995). QED Coherence in Matter. Princeton paperbacks. World Scientific Pub Co Inc. p. ۱۴۵. ISBN 9810222491. Archived from the original on 29 July 2013. Retrieved 8 November 2011.
- ↑ Kovacs, Z.; Cheng, K. S.; Harko, T. (2009). "Can stellar mass black holes be quark stars?". Monthly Notices of the Royal Astronomical Society. ۴۰۰ (۳): ۱۶۳۲–۱۶۴۲. arXiv:۰۹۰۸٫۲۶۷۲. Bibcode:2009MNRAS.400.1632K. doi:10.1111/j.1365-2966.2009.15571.x.
{{cite journal}}: Check|arxiv=value (help) - ↑ Kusenko, A. (2006). "Properties and signatures of supersymmetric Q-balls". arXiv:hep-ph/0612159.
- ↑ Hansson, J.; Sandin, F. (2005). "Preon stars: a new class of cosmic compact objects". Physics Letters B. ۶۱۶ (۱–۲): ۱. arXiv:astro-ph/0410417. Bibcode:2005PhLB..616....1H. doi:10.1016/j.physletb.2005.04.034.
- ↑ Kiefer, C. (2006). "Quantum gravity: general introduction and recent developments". Annalen der Physik. ۱۵ (۱–۲): ۱۲۹. arXiv:gr-qc/0508120. Bibcode:2006AnP...518..129K. doi:10.1002/andp.200510175.
- ↑ Skenderis, K.; Taylor, M. (2008). "The fuzzball proposal for black holes". Physics Reports. ۴۶۷ (۴–۵): ۱۱۷. arXiv:۰۸۰۴٫۰۵۵۲. Bibcode:2008PhR...467..117S. doi:10.1016/j.physrep.2008.08.001.
{{cite journal}}: Check|arxiv=value (help) - ↑ Hawking, S. W. (1971). "Gravitational Radiation from Colliding Black Holes". Physical Review Letters. ۲۶ (۲۱): ۱۳۴۴–۱۳۴۶. Bibcode:1971PhRvL..26.1344H. doi:10.1103/PhysRevLett.26.1344.
- ↑ ۱۳۸٫۰ ۱۳۸٫۱ Wald, R. M. (2001). "The Thermodynamics of Black Holes". Living Reviews in Relativity. ۴ (۶). arXiv:gr-qc/9912119. Bibcode:1999gr.qc....12119W. Archived from the original on 22 January 2020. Retrieved 2011-02-10.
- ↑ 't Hooft, G. (2001). "The Holographic Principle". In Zichichi, A. (ed.). Basics and highlights in fundamental physics. Subnuclear series. Vol. ۳۷. World Scientific. arXiv:hep-th/0003004. ISBN 9789810245368.
- ↑ Strominger, A.; Vafa, C. (1996). "Microscopic origin of the Bekenstein-Hawking entropy". Physics Letters B. ۳۷۹ (۱–۴): ۹۹. arXiv:hep-th/9601029. Bibcode:1996PhLB..379...99S. doi:10.1016/0370-2693(96)00345-0.
- ↑ Carlip, S. (2009). "Black Hole Thermodynamics and Statistical Mechanics". Lecture Notes in Physics. ۷۶۹: ۸۹. arXiv:۰۸۰۷٫۴۵۲۰. doi:10.1007/978-3-540-88460-6_3.
{{cite journal}}: Check|arxiv=value (help) - ↑ Hawking, S. W. "Does God Play Dice?". www.hawking.org.uk. Archived from the original on 3 November 2011. Retrieved 2009-03-14.
- ↑ «HubbleSite: "How many black holes are there?"». بایگانیشده از روی نسخه اصلی در ۳ فوریه ۲۰۱۴. دریافتشده در ۸ نوامبر ۲۰۱۱.
- ↑ Poplawski, N. J. (2010). "Radial motion into an Einstein-Rosen bridge". Physics Letters B. ۶۸۷: ۱۱۰. Bibcode:2010PhLB..687..110P. doi:10.1016/j.physletb.2010.03.029.
- ↑ «Indiana University Newsroom: "Our universe at home within a larger universe? So suggests IU theoretical physicist's wormhole research"». بایگانیشده از روی نسخه اصلی در ۱۹ نوامبر ۲۰۱۱. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ «National Geographic Daily News: "Every Black Hole Contains Another Universe?"». بایگانیشده از روی نسخه اصلی در ۱۳ دسامبر ۲۰۱۷. دریافتشده در ۴ ژانویه ۲۰۱۱.
- ↑ «Science Now: "Does Our Universe Live Inside a Wormhole?"». بایگانیشده از اصلی در ۲۱ اوت ۲۰۱۱. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ «Space.com: "Our Universe Was Born in a Black Hole, Theory Says"». بایگانیشده از روی نسخه اصلی در ۶ ژانویه ۲۰۱۱. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ «National Geographic Daily News: "Top Ten Discoveries of 2010: Nat Geo News's Most Popular"». بایگانیشده از روی نسخه اصلی در ۳ نوامبر ۲۰۱۱. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ «Science Now: "Top 10 ScienceNOWs of 2010"». بایگانیشده از اصلی در ۷ نوامبر ۲۰۱۱. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ Smolin, L. (1992). "Did the Universe evolve?". Classical and Quantum Gravity. ۹: ۱۷۳. doi:10.1088/0264-9381/9/1/016.
- ↑ «New Scientist, Vol. 207, No. 2770, p. 9 (2010): "Every black hole may hold a hidden universe"». بایگانیشده از روی نسخه اصلی در ۴ نوامبر ۲۰۱۱. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ «Washington Post: "Cosmologist's theory about black holes puts a new spin on the universe"». بایگانیشده از روی نسخه اصلی در ۱۱ نوامبر ۲۰۱۲. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ Poplawski, N. J. (2010). "Cosmology with torsion: An alternative to cosmic inflation". Physics Letters B. ۶۹۴: ۱۸۱. doi:10.1016/j.physletb.2010.09.056.
- ↑ «Popular Science: "Are We Living Inside a Black Hole?"». بایگانیشده از روی نسخه اصلی در ۵ اکتبر ۲۰۱۲. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ «National Post: "We may exist inside a black hole, scientist says"». بایگانیشده از روی نسخه اصلی در ۲۵ ژوئیه ۲۰۱۱. دریافتشده در ۷ نوامبر ۲۰۱۱.
- ↑ «Telegraph: "A universe could exist 'inside every black hole,' claims scientist"». بایگانیشده از روی نسخه اصلی در ۲۸ ژانویه ۲۰۱۱. دریافتشده در ۴ ژانویه ۲۰۱۱.
- ↑ Pathria, R. K. (1972). "The Universe as a Black Hole". Nature. ۲۴۰ (۵۳۷۹): ۲۹۸. doi:10.1038/240298a0.
- ↑ Wolfson, Richard (2002). Simply Einstein: relativity demystified. W. W. Norton & Company. p. ۲۶۱. ISBN 0-393-05154-4.
- ↑ "Frontiers And Controversies In Astrophysics Transcript 9". Yale University. Retrieved April 26, 2011.[پیوند مرده]
- ↑ "Frontiers And Controversies In Astrophysics Transcript 9". Yale University. Archived from the original on 9 March 2016. Retrieved April 26, 2011.
- ↑ https://www.nasa.gov/mission_pages/chandra/news/new-nasa-black-hole-sonifications-with-a-remix.html





