انتگرال

نمایش گرافیکی انتگرال.

اَنتِگرال، برای اشاره به انتگرال معیّن (به انگلیسی: definite integral) یا انتگرال نامعیّن (به انگلیسی: indefinite integral) به‌کار می‌رود.

اَنتِگرال معینِ تابع $f$ از متغیر حقیقی $x$ در بازه $[a,b]$، برابر است با مساحت ناحیه محصور میان نمودار این تابع، محور $x$، و مرزهای $x=a$ و $x=b$. حاصل انتگرال معین، می‌تواند مقداری مثبت، منفی، یا صفر باشد.

اَنتِگرال نامعین را می‌توان عکس مشتق به‌حساب آورد.

انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عمل اصلی حساب دیفرانسیل و انتگرال را تشکیل می‌دهند.

نخستین بار لایب‌نیتس نماد استانداردی برای انتگرال معرفی کرد.

$\int _{a}^{b}f(x)\,dx$

$a$ و $b$ نقاط ابتدا و انتهای بازه هستند و $f(x)$ تابعی انتگرال‌پذیر است و $dx$ نمادی برای متغیر انتگرال‌گیری است.

از لحاظ تاریخی $dx$ یک کمیت بی‌نهایت کوچک را نشان می‌دهد. هر چند در تئوری‌های جدید، انتگرال بر پایه متفاوتی بنا شده‌است.

انتگرال نامعین

هرگاه مشتق تابعی معلوم باشد و بخواهیم تابع را مشخص کنیم، این عمل را انتگرال‌ نامعین نامیده و آن را با نماد $\int$ نمایش می‌دهیم. به انتگرال نامعین، پادمشتق نیز گفته‌می‌شود، زیرا انتگرال نامعین، عکس مشتق‌ است.

بنا به تعریف، نماد $\int {f(x)}.dx$ را انتگرال نامعین نامیده و حاصل آن را تابعی مانند $F(x)+c$ در نظر می‌گیریم هرگاه:

$\int {f(x)}.dx=F(x)+c$

که $c$ مقداری ثابت است. در واقع می‌توان چنین بیان کرد:

$F'(x)=f(x)\Leftrightarrow \int {f(x)}.dx=F(x)+c$

مثال: مقدار انتگرال تابع $f(x)={\sqrt {x}}+2x^{2}-8$ را حساب کنید:

$\int {f(x)}.dx=\int {(x^{\frac {1}{2}}+2x^{2}-8)}.dx=\int {x^{\frac {1}{2}}}.dx+2\int {x^{2}}.dx-8\int {dx}={\frac {2}{3}}x^{\frac {3}{2}}+{\frac {2}{3}}x^{3}-8x+C$

$\Rightarrow \int {f(x)}.dx={\frac {2}{3}}x{\sqrt {x}}+{\frac {2}{3}}x^{3}-8x+C$

انتگرال معین

مقالهٔ اصلی: پاد مشتق

بنا به تعریف، نماد $\int _{a}^{b}f(x).dx$ را انتگرال معین نامیده و حاصل آن را به ازای $a<x<b$ عددی به صورت زیر تعریف می‌کنیم:

انتگرال معین یک تابع می‌تواند به عنوان علامت مساحت ناحیه محدود شده با گرافش نشان داده شود.

$\int _{a}^{b}f(x).dx=F(x)|_{a}^{b}=F(b)-F(a)$

$a$ و $b$ به ترتیب، کران‌های بالا و پایین انتگرال نامیده می‌شوند.

تابع انتگرال‌پذیر

اگر تابعی دارای انتگرال باشد به آن انتگرال‌پذیر گویند.

تعبیر هندسی انتگرال

از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.

نکته انتگرال نمودار سه بعدی(انتگرال دوگانه) معرف حجم محصور زیر نمودار است و انتگرال سه‌گانه معرف پارالل زیر نمودار است (غیرقابل تصور).

مثال

انتگرال یک تابع مثبت پیوسته در بازه (۰٬۱۰) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=۱۰ و خم منحنی $f_{x}$ است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال‌پذیر است و dx نمادی برای متغیر انتگرال‌گیری است.

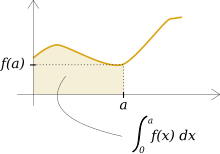
انتگرال یک تابع مساحت زیر نمودار آن تابع است.

انتگرال‌گیری

(محاسبه انتگرال) انتگرال‌گیری به معنی محاسبه سطح زیر نمودار با استفاده از روش‌ها و قوانین انتگرال‌گیری است(انتگرال معین). انتگرال را می‌توان عمل عکس مشتق معرفی نمود (انتگرال نامعین).

مهم‌ترین تعاریف در انتگرال

مثالی از انتگرال با تقسیمات ناهمسان(بزرگترین قسمت با رنگ قرمز مشخص شده است)

همگرایی مجموع‌های ریمان

از مهم‌ترین تعاریف در انتگرال می‌توان از انتگرال ریمان و انتگرال لِبِگ است. انتگرال ریمان به‌وسیله برنهارد ریمان در سال ۱۸۵۴ ارائه شد که تعریف دقیقی را از انتگرال ارائه می‌داد تعریف دیگر را هانری لبگ ارائه داد که طبق این تعریف شرایط تعویض‌پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می‌کرد. از دیگر تعاریف ارائه شده در زمینه انتگرال می‌توان به انتگرال ریمان–استیلتیس اشاره کرد. پس به‌طور خلاصه سه تعریف زیر از مهم‌ترین تعاریف انتگرال می‌باشند:

محاسبه انتگرال

Approximations to integral of √x from 0 to 1, with 5 ■ (yellow) right endpoint partitions and 12 ■ (green) left endpoint partitions

اکثر روش‌های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده‌است که بر طبق آن داریم:

1. f تابعی در بازه (a,b) در نظر می‌گیریم.
2. پاد مشتق f را پیدا می‌کنیم که تابعی است مانند f .
3. قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می‌گیریم.

بنابراین مقدار انتگرال ما برابر خواهد بود.

به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می‌دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار ساده‌ای نیست و نیاز به استفاده از تکنیک‌های انتگرال‌گیری دارد این تکنیک‌ها عبارت‌اند از:

• انتگرال‌گیری به‌وسیله تغییر متغیر
• انتگرال‌گیری جزء به جزء: $\int u\,dv=uv-\int v\,du$
• انتگرال‌گیری با تغییر متغیر مثلثاتی
• انتگرال‌گیری به‌وسیله تجزیه کسرها

روش‌هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می‌رود همچنین می‌توان بعضی از انتگرال‌ها با ترفندهایی حل کرد برای مثال می‌توانید به انتگرال گاوسی مراجعه کنید.

تقریب انتگرال‌های معین

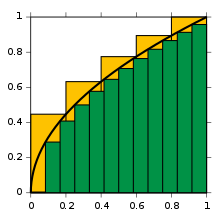
محاسبه سطح زیر نمودار به‌وسیله مستطیل‌هایی زیر نمودار. هر چه قدر عرض مستطیل‌ها کوچک می‌شوند مقدار دقیق تری از مقدار انتگرال بدست می‌آید.

انتگرال‌های معین ممکن است با استفاده از روش‌های انتگرال‌گیری عددی، تخمین زده شوند. یکی از عمومی‌ترین روش‌ها، روش مستطیلی نامیده می‌شود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آن‌ها نشان دهنده مقدار تقریبی انتگرال است. از دیگر روش‌هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقه‌ای است. اگر چه روش‌های عددی مقدار دقیق انتگرال را به ما نمی‌دهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما می‌کند.

Darboux sums

Darboux upper sums of the function y = x²

Darboux lower sums of the function y = x²

کاربرد

انتگرال‌ها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک می‌توان برای کاربردهای زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست می‌آید. اما به‌طور کلی می‌توان آن را تغییرات کمیت حاصل ضرب افقی و عمودی نمودار نامید مثلاً: در یک رابطه کمیت‌ها را تحلیل ابعادی می‌کنیم مثلاً رابطه سرعت و زمان را به صورت زیر نوشته می‌شود:

$v=[L]/[T]t=[T]\!$

سپس دو تحلیل را در هم ضرب می‌کنیم:

$[L]\!$

پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.

جستارهای وابسته

• جدول مختصر انتگرال‌ها
• انتگرال چندگانه

منابع

• ویکی‌پدیای انگلیسی

تاریخچه

• Meyer Hirsch, Integraltafeln, oder, Sammlung von Integralformeln (Duncker und Humblot, Berlin, 1810)
• Meyer Hirsch, Integral Tables, Or, A Collection of Integral Formulae (Baynes and son, London, 1823) [English translation of Integraltafeln]
• David Bierens de Haan, Nouvelles Tables d'Intégrales définies (Engels, Leiden, 1862)
• Benjamin O. Pierce A short table of integrals - revised edition (Ginn & co. , Boston, 1899)

پیوند به بیرون

• ماشین انتگرال‌گیر برای نمونه معادله $\int {cos^{3}(1-x)}.dx$ در این لینک موجود است.