از ویکی‌پدیا، دانشنامهٔ آزاد
تابع توزیع تجمعی برای توزیع نرمال .
تابع چگالی احتمال برای چند توزیع نرمال، نمودار قرمز رنگ مربوط به توزیع نرمال استاندارد است ..
تابع توزیع تجمعی (به انگلیسی : Cumulative distribution function تابع توزیع انباشتی تابعی غیر صفر و هم نوای صعودی است که برد آن بازه [۰٫۱] بوده و احتمال آنکه متغیر تصادفی X دارای مقداری کوچک‌تر از x باشد را نشان می‌دهد،[۱]
x
→
F
X
(
x
)
=
P
(
X
≤
x
)
{\displaystyle x\to F_{X}(x)=\operatorname {P} (X\leq x)}
[۲]
از این تعریف می‌توان نتیجه گرفت که:
P
(
a
<
X
≤
b
)
=
F
X
(
b
)
−
F
X
(
a
)
{\displaystyle P(a<X\leq b)=F_{X}(b)-F_{X}(a)}
تابع توزیع تجمعی را می‌توان به صورت زیر بر اساس تابع چگالی احتمال نیز تعریف کرد
F
(
x
)
=
∫
−
∞
x
f
(
t
)
d
t
.
{\displaystyle F(x)=\int _{-\infty }^{x}f(t)\,dt.}
[۳]
در مورد متغیرهای تصادفی با مقادیر گسسته این تعریف به صورت زیر است:
Pr
(
X
=
x
)
=
F
(
x
0
)
−
F
(
x
0
−
)
,
{\displaystyle \Pr(X=x)=F(x_{0})-F(x_{0}-),}
که در اینجا
F
(
x
0
−
)
{\displaystyle F(x_{0}-)}
F
X
(
x
)
{\displaystyle F_{X}(x)}
x
{\displaystyle x}
x
0
{\displaystyle x_{0}}
[۱]
خواص تابع توزیع تجمعی [ ویرایش ] تابع توزیع تجمعی برای متغیر تصادفی گسسته به این شکل تعریف می‌شود:
F
X
(
x
)
=
P
(
X
≤
x
)
=
∑
t
≤
x
P
(
t
)
{\displaystyle F_{X}(x)=P(X\leq x)=\sum _{t\leq x}P(t)}
نمودار تابع توزیع تجمعی برای متغیر تصادفی گسسته
تعریف تابع توزیع تجمعی برای متغیر تصادفی پیوسته به این شکل می‌شود :
F
X
(
x
)
=
P
(
X
≤
x
)
=
∫
t
≤
x
f
(
t
)
d
t
{\displaystyle F_{X}(x)=P(X\leq x)=\int _{t\leq x}f(t)dt}
تمام توابع توزیع تجمعی صعودی (ولی نه لزوماً اکیدا صعودی) و از راست پیوسته هستند.
0
≤
F
X
(
x
)
≤
1
{\displaystyle 0\leq F_{X}(x)\leq 1}
lim
x
→
−
∞
F
(
x
)
=
0
{\displaystyle \lim _{x\to -\infty }F(x)=0}
lim
x
→
+
∞
F
(
x
)
=
1
{\displaystyle \lim _{x\to +\infty }F(x)=1}
[۱] اگر
x
1
≤
x
2
{\displaystyle x_{1}\leq x_{2}}
F
X
(
x
1
)
≤
F
X
(
x
2
)
{\displaystyle F_{X}(x_{1})\leq F_{X}(x_{2})}
P
(
X
>
x
)
=
1
−
F
X
(
x
)
{\displaystyle P(X>x)=1-F_{X}(x)}
P
(
x
1
<
x
≤
x
2
)
=
F
X
(
x
2
)
−
F
X
(
x
1
)
{\displaystyle P(x_{1}<x\leq x_{2})=F_{X}(x_{2})-F_{X}(x_{1})}
اگر M میانه داده‌ها باشد داریم :
F
X
(
M
)
=
∫
−
∞
M
f
(
x
)
d
x
=
1
2
{\displaystyle F_{X}(M)=\int _{-\infty }^{M}f(x)dx={\frac {1}{2}}}
و این همان تعریف میانه است که نیمی از داده‌ها مقداری کمتر از M دارند.[۴]
فرض کنید X یک متغیر تصادفی پیوسته‌است که تابع چگالی احتمال آن به این شکل تعریف شده باشد:[۵]
f
(
x
)
=
{
0
x
≤
−
1
x
+
1
−
1
<
x
≤
0
1
−
x
0
<
x
<
1
0
x
≥
1
{\displaystyle f(x)={\begin{cases}0&x\leq -1\\\\x+1&-1<x\leq 0\\\\1-x&0<x<1\\\\0&x\geq 1\end{cases}}}
نمودار چگالی احتمال این متغیر تصادفی به شکل زیر خواهد بود:
نمودار تابع چگالی احتمال این مثال
با انتگرال‌گیری از تابع چگالی احتمال در هر بازه تابع توزیع تجمعی آن را به دست می‌آوریم و خواهیم داشت:
F
(
x
)
=
{
0
x
≤
−
1
1
2
(
x
+
1
)
2
−
1
<
x
≤
0
1
−
(
1
−
x
)
2
2
0
<
x
<
1
1
x
≥
0
{\displaystyle F(x)={\begin{cases}0&x\leq -1\\\\{\frac {1}{2}}(x+1)^{2}&-1<x\leq 0\\\\1-{\frac {(1-x)^{2}}{2}}&0<x<1\\\\1&x\geq 0\end{cases}}}
نمودار تابع توزیع تجمعی این مثال
تابع توزیع تجمعی برای چند توزیع [ ویرایش ] در این قسمت تابع توزیع تجمعی چند توزیع معروف و نمودار توزیع تجمعی آن‌ها را بررسی می‌کنیم:
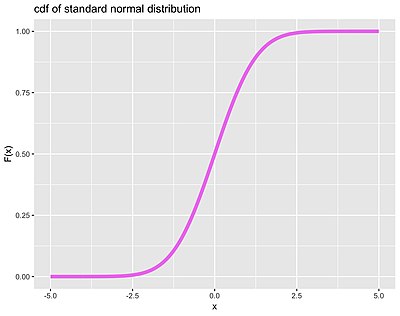
توزیع طبیعی استاندارد [ ویرایش ] تابع چگالی احتمال توزیع طبیعی استاندارد برای ℝ
x
∈
{\displaystyle x\in }
f
(
x
)
=
1
2
π
e
−
x
2
2
{\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}e^{\frac {-x^{2}}{2}}}
و تابع توزیع تجمعی آن برابر است با:
F
(
x
)
=
∫
f
(
x
)
d
x
=
∫
1
2
π
e
−
x
2
2
=
1
2
(
1
+
e
r
f
x
−
μ
σ
2
)
{\displaystyle F(x)=\int f(x)dx=\int {\frac {1}{\sqrt {2\pi }}}e^{\frac {-x^{2}}{2}}={\frac {1}{2}}\left(1+{\mathrm {erf} }\,{\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\!}
نمودار تابع توزیع تجمعی برای توزیع طبیعی استاندارد
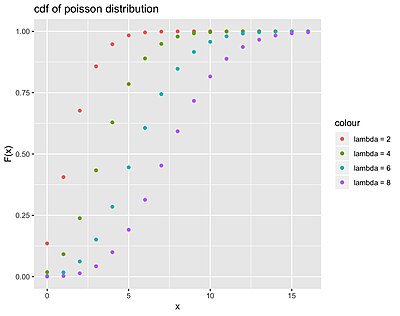
توزیع پواسون [ ویرایش ] تابع جرم احتمال توزیع پواسون برای {1,2,3,...}
k
∈
{\displaystyle k\in }
λ
∈
(
0
,
∞
)
{\displaystyle \lambda \in (0,\infty )}
P
(
x
)
=
e
−
λ
λ
k
k
!
{\displaystyle P(x)={\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}\!}}
و تابع توزیع تجمعی آن برابر است با:
F
(
x
)
=
∑
P
(
x
)
=
∑
e
−
λ
λ
k
k
!
=
Γ
(
k
+
1
,
λ
)
k
!
{\displaystyle F(x)=\sum P(x)=\sum {\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}\!}={\displaystyle {\frac {\Gamma (k+1,\lambda )}{k!}}\!}}
نمودار تابع توزیع تجمعی برای چند توزیع دلخواه پواسون
توزیع نمایی [ ویرایش ] تابع چگالی احتمال توزیع نمایی برای
x
≥
0
{\displaystyle x\geq 0}
f
(
x
)
=
λ
e
−
λ
x
{\displaystyle f(x)=\lambda e^{-\lambda x}}
و تابع توزیع تجمعی آن برابر است با:
F
(
x
)
=
∫
f
(
x
)
d
x
=
∫
λ
e
−
λ
x
=
1
−
e
−
λ
x
{\displaystyle F(x)=\int f(x)dx=\int \lambda e^{-\lambda x}=1-e^{-\lambda x}}
نمودار تابع توزیع تجمعی برای چند توزیع دلخواه نمایی
تابع توزیع تجمعی برای توابع توام [ ویرایش ] تابع توزیع تجمعی برایتوزیع احتمال توأم به این صورت تعریف می‌شود:
F
X
1
,
X
2
,
.
.
.
,
X
n
(
x
1
,
x
2
,
.
.
.
.
,
x
n
)
=
P
(
X
1
≤
x
1
,
X
2
≤
x
2
,
.
.
.
,
X
n
≤
x
n
)
{\displaystyle F_{X_{1},X_{2},...,X_{n}}(x_{1},x_{2},....,x_{n})=P(X_{1}\leq x_{1},X_{2}\leq x_{2},...,X_{n}\leq x_{n})}
با این تعریف تابع توزیع تجمعی برای تابع دو متغیره
f
X
Y
(
x
,
y
)
{\displaystyle f_{XY}(x,y)}
F
X
Y
(
x
,
y
)
=
P
(
X
≤
x
,
Y
≤
y
)
{\displaystyle F_{XY}(x,y)=P(X\leq x,Y\leq y)}
ویژگی‌های این تابع همانند حالت یک متغیره خواهد بود. برخی از این ویژگی‌ها عبارتند از:
0
≤
F
X
1
,
X
2
,
.
.
.
,
X
n
(
x
1
,
x
2
,
.
.
.
.
,
x
n
)
≤
1
{\displaystyle 0\leq F_{X_{1},X_{2},...,X_{n}}(x_{1},x_{2},....,x_{n})\leq 1}
lim
x
1
,
x
2
,
.
.
.
,
x
n
→
−
∞
F
X
1
,
X
2
,
.
.
.
,
X
n
(
x
1
,
x
2
,
.
.
.
.
,
x
n
)
=
0
{\displaystyle \lim _{x_{1},x_{2},...,x_{n}\to -\infty }F_{X_{1},X_{2},...,X_{n}}(x_{1},x_{2},....,x_{n})=0}
lim
x
1
,
x
2
,
.
.
.
,
x
n
→
∞
F
X
1
,
X
2
,
.
.
.
,
X
n
(
x
1
,
x
2
,
.
.
.
.
,
x
n
)
=
1
{\displaystyle \lim _{x_{1},x_{2},...,x_{n}\to \infty }F_{X_{1},X_{2},...,X_{n}}(x_{1},x_{2},....,x_{n})=1}
P
(
x
1
<
x
≤
x
2
,
y
1
<
y
≤
y
2
)
=
F
X
Y
(
x
2
,
y
2
)
−
F
X
Y
(
x
1
,
y
2
)
−
F
X
Y
(
x
2
,
y
1
)
+
F
X
Y
(
x
1
,
y
1
)
{\displaystyle P(x_{1}<x\leq x_{2},y_{1}<y\leq y_{2})=F_{XY}(x_{2},y_{2})-F_{XY}(x_{1},y_{2})-F_{XY}(x_{2},y_{1})+F_{XY}(x_{1},y_{1})}
[۶]
↑ ۱٫۰ ۱٫۱ ۱٫۲ http://en.wikipedia.org/w/index.php?title=Cumulative_distribution_function&oldid=437556047 ↑ Probability and Statistics in Engineering And Management Science, William W. Hines, Douglas C. Montgomery, Third Edition, John Wiley and Sons, 1990, ISBN 0-471-60090-3 .
↑ Introduction to Probability
Models, Sheldon M. Ross, Tenth Edition
↑ «نسخه آرشیو شده» (PDF) . بایگانی‌شده از اصلی (PDF) در ۳۱ اکتبر ۲۰۱۷. دریافت‌شده در ۲۸ دسامبر ۲۰۱۸ .↑ «نسخه آرشیو شده» . بایگانی‌شده از اصلی در ۲۸ دسامبر ۲۰۱۸. دریافت‌شده در ۲۸ دسامبر ۲۰۱۸ .↑ https://www.probabilitycourse.com/chapter5/5_2_2_joint_cdf.php
