حالت همدوس

حالت همَدوس (به انگلیسی: Coherent states) در مکانیک کوانتومی نوع خاصی از حالت کوانتومی است که دینامیکش تقریباً به رفتار نوسانی یک نوسانگر هارمونیک کلاسیک شباهت دارد؛ و اولین نمونه دینامیک کوانتومی بود که اروین شرودینگر در سال ۱۹۲۶ آن را؛ هنگامی که در جستجوی حل معادله شرودینگری بود که در اصل تطابق صدق کند نتیجه گرفت. نوسانگر هماهنگ کوانتومی و از اینرو، حالت همدوس، از نظریه کوانتومی یک دامنه گسترده ازسیستم فیزیکی ناشی می‌شود. برای مثال، حالت همدوس، با حرکت نوسانی ذره‌ای که در چاه پتانسیل مربعی محبوس است به خوبی توصیف می‌شود. این حالت‌ها در نظریه کوانتومی نور (الکترودینامیک کوانتومی) و دیگر نظریه‌های میدان کوانتومی بوزونی، توسط کار گلاوبر در سال ۱۹۶۳ معرفی شدند. در اینجا حالت همدوس یک میدان با یک میدان نوسانی حالت کوانتومی مربوط به یک موج سینوسی کلاسیکی مثل موج لیزر پیوسته، توصیف می‌شود...

حالت‌های همدوس در اپتیک کوانتومی

شکل ۱. میدان الکتریکی اندازه‌گیری شده توسط آشکارساز هومودین به صورت یک تابع فاز برای سه حالت همدوس منتشر شده از یک Nd: YAG. مقدار نوفه کوانتومی در میدان الکتریکی کاملاً مستقل از فاز است. وقتی که قدرت میدان، یعنی دامنه نوسان a ی حالت همدوس افزایش می‌یابد، نوفه کوانتومی یاعدم قطعیت در ۱/۲ثابت است. وهمچنین کمتر و کم‌اهمیت تر می‌شود. در محدوده میدان بزرگ حالت یک تقریب خوب از موج کلاسیکی پایای بدون نوفه وجود دارد. اعداد فوتونی میانگین سه حالت از بالا تا پایین عبارتند از: n>= ۴٫۲٬۲۵٫۲٬۹۲۴. (منبع: پیوند ۱ و مرجع 2)

شکل ۲. نوسان بسته موج متناظر با دومین حالت همدوس نمایش داده شده در شکل ۱. در هر یک از فازهای میدان نوری، توزیع گاوسی است با پهنای ثابت.

شکل ۳. تابع وینگرحالت همدوس نمایش داده شده در شکل ۲. توزیعی که روی دامنه حالت‌ها a جمع شده و حول این نقطه متقارن شده‌است. موج دار شدگی ناشی از خطاهای آزمایشگاهی است.

در مکانیک کوانتومی حالت همدوس نوع خاصی از حالت کوانتومی، که در نوسانگر هماهنگ کوانتومی، میدان الکترو مغناطیسی و… خیلی پرکاربرد است؛ نوع همدوسی بیشینه و نوع رفتار کلاسیکی را توصیف می‌کند. اروین شرودینگر در سال ۱۹۲۶ آن، بسته موج گاوسی با عدم قطعیت کمینه، را وقتی که در حال جستجوی حل معادله شرودینگری که در اصل تطابق صدق کندبود، بدست آورد. حالتی با کمترین عدم قطعیت با تنها پارامتر مستقل انتخاب شده برای ایجاد پاشندگی نسبی، (انحراف معیار تقسیم بر میانگین) برابر با مکان و تکانه، هر یک در انرژی بالا به‌طور یکسان کوچک می‌شوند؛ بنابراین وقتی که مقدار انتظاری معادلات حرکت هایزنبرگ صفر هستند به ازای همه ویژه حالت‌های انرژی سیستم، در یک حالت همدوس مقدار چشمداشتی معادلات حرکت دقیقاً معادلات حرکت کلاسیکی هستند و فقط در انرژی بالا پراکندگی کوچکی دارند. (انرژی بالا در صورتی ایجاد می‌شود که دامنه نوسانی میانگین و تکانه مقادیر کلاسیکی کوچکی داشته باشند) نوسانگرهماهنگ کوانتومی و از اینرو، حالت همدوس، از نظریه کوانتومی یک دامنه گسترده از سیستم فیزیکی ناشی می‌شود؛ و همچنین در نظریه کوانتومی نور (الکترودینامیک کوانتومی) و دیگر نظریه‌های میدان کوانتومی بوزونی یافت می‌شوند.

هنگامی که بسته‌های موج گاوسی با عدم قطعیت کمینه معروف شدند، توجه زیادی را جلب نکردند تا اینکه گلاوبردر سال ۱۹۶۳، توصیف کوانتوم- نظری کاملی ازهمدوسی در میدان الکترومغناطیسی تهیه کرد.

گلاوبر برای انجام این کار به منظور توصیف آزمایش توایس و هانبری– براون که خط مبنا (صدها یا هزارها مایل) ی الگوهای تداخلی خیلی وسیعی که می‌تواند در تعیین قطر ستاره‌ها استفاده شود، ترغیب شد و به این ترتیب کار او دری به روی درک جامع تری از همدوسی باز کرد.

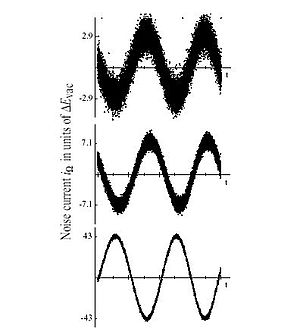
در اپتیک کلاسیکی، نور به صورت تابش الکترومغناطیسی از یک منبع تصور می‌شود. اغلب، نور لیزر همدوس به صورت نوری تصور می‌شود که توسط چنین منابع زیادی که هم فاز هستند، منتشر می‌شود. در حقیقت، تصور یک فوتون که با دیگری هم فاز باشد در نظریه کوانتومی قابل اطمینان نیست. تابش لیزر در یک کاواک تشدیدی تولید می‌شود که فرکانس تشدیدی کاواک با فرکانس هم بسته به گذار اتمی که جریان انرژی در میدان را فراهم می‌کند یکسان است. از آنجایی که انرژی در مد تشدیدی ذخیره می‌شود، احتمال برای گسیل القایی تنها در آن مد افزایش می‌یابد. این یک حلقه باز خورد مثبت است که دامنه اش در مد تشدیدی به صورت نمایی افزایش می‌یابد تا زمانی که اثرات غیر خطی آن را محدود کند. به عنوان یک ضد مثال، لامپ نوری به صورت مدهای پیوستار نور می‌تاباند، و هیچ انتخابی برای مدهای بالاتر دیگر وجود ندارد. مدهای فرایند گسیل در فضا و زمان کاملاً تصادفی است (نگاه کنید به نور حرارتی). در یک لیزر، هر چند، نور به صورت یک مد تشدیدی منتشر می‌شود مد آن کاملاً همدوس است؛ بنابراین، نور لیزردر حالت ایده‌آل به صورت یک حالت همدوس است. (به صورت کلاسیکی چنین حالتی را با یک میدان الکتریکی که به صورت موج پایدار نوسان می‌کند توصیف می‌کنیم). به شکل ۱ نگاه کنید.

ویژه حالت‌های انرژی نوسانگر هماهنگ خطی (برای مثال جرم متصل به فنر، ارتعاشات شبکه در یک جامد، یا نوسانات میدان الکترو مغناطیسی) حالت‌های کوانتومی عدد- ثابت هستند. حالت فوک (مثلاً فوتون منفرد) حالت شبه ذره‌است، که عدد- ثابت ذرات را دارا است، و فاز نا معین است. یک حالت همدوس عدم قطعیت کوانتوم – مکانیکی اش را به‌طور مساوی بین مختصات توأم استاندارد، مکان و تکانه، تقسیم می‌کند و عدم قطعیت نسبی در فاز تعریف شده و دامنه تقریباً برابر و کوچکتر از دامنه اصلی هستند.

تعریف مکانیک کوانتومی

به صورت ریاضیاتی حالت همدوس$|\alpha >\,$ به صورت ویژه حالت ' راست ' عملگر نابودی${\hat {a}}\,$ تعریف می‌شود. ظاهراً، به این معنی است:

${\hat {a}}\,|\alpha \,>=\alpha \,|\alpha >$

از آن جایی که ${\hat {a}}$ هرمیتی نیست، $\alpha \,$ یک عدد مختلط است، که در حقیقت می‌توان به صورت زیر نمایش داد:

$\alpha \,=|\alpha \,|e^{i\theta \,}$ که $\theta \,$ عددی حقیقی است. اینجا $|\alpha |\,$ و $\theta \,$ به ترتیب دامنه و فاز حالت نامیده می‌شوند.

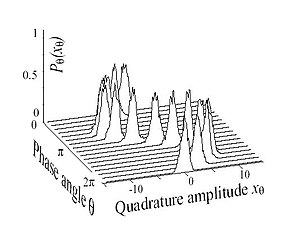
به‌طور فیزیکی، این فرمول به این معنی است که حالت همدوس با آشکار سازی (یا نابودی) یک ذره به چپ جابه‌جا نمی‌شود. ویزه عملگر نابودی توزیع عددی پواسونی دارد (به صورت نشان داده شده در زیر). توزیع پواسونی شرط لازم و کافی است که همه آشکار سازی‌ها مستقلاً آماری باشند. این را با یک حالت تک-ذره (حالت فوک $|1>\,$)مقایسه کنید: هر بار که ذره آشکار می‌شود، احتمال آشکار کردن دیگری صفر می‌شود. مشتق گیری این کاربرد مربع‌ها ی $X$ و $P$ بدون بعد را فراهم می‌کند. این مربع‌ها مربوط به مکان و تکانه جرمی در یک نوسانگر جرم و فنر است:

$X=x{\sqrt {\frac {m\omega \,}{2\hbar }}}$ و $P=p{\sqrt {\frac {1}{2\hbar m\omega \,}}}$ و $\omega \equiv {\sqrt {\frac {k}{m}}}$

برای یک میدان اپتیکی،

$E_{R}=X\cos \theta {\sqrt {\frac {\hbar \omega \,}{2\epsilon \,V}}}$ و $E_{I}=P\sin \theta {\sqrt {\frac {\hbar \omega \,}{2\epsilon \,V}}}$

$E_{R}$ و $E_{I}$ مولفه‌ها ی حقیقی و موهومی مد میدان الکتریکی هستند.

با این مربع‌ها، هامیلتونی هر یک از سیستم‌ها می‌شود:

$H=\hbar \omega \left(X^{2}+P^{2}\right)$

$\left[X,P\right]\equiv \,XP-PX={\frac {i}{2}}$

اروین شرودینگر روی حالت‌ها ی شبه کلاسیک تحقیق می‌کرد که برای اولین بار بسته‌های موجی گاوسی با کمترین عدم قطعیت را تو لید کرد. حالت کوانتومی نوسانگر هماهنگ که رابطه عدم قطعیت را با توزیع یکسان عدم قطعیت در مربع‌های X و P که در معادله زیر صدق می‌کنند، کمینه می‌سازد.

$\left(P-\left\langle P\right\rangle \right)|\alpha >=i\left(X-\left\langle X\right\rangle \right)|\alpha >$ یا $\left(P-iX\right)|\alpha >=\left\langle P-iX\right\rangle |\alpha >$

که ویژه حالت عملگر $\left(X-iP\right)$ است. (اگر عدم قطعیت بین X و P متعادل نباشد، حالا، حالت همدوس فشرده نامیده می‌شود). شرودینگر حالت‌هایی با عدم قطعیت کمینه را برای نوسانگر هارمونیک خطی پیدا کرد که ویژه حالت‌های $\left(X-iP\right)$ می‌باشند؛ و با استفاده از نماد گذاری برای حالت‌های چند – فوتونی، گلاوبر حالت همدوسی کامل همه مراتب را در میدان الکترو مغناطیسی پیدا کرد که ویژه حالت راست عملگر نابودی می‌باشند، ظاهراً برای درک ریاضی، همان نام «حالت همدوس» بعد از کار گلاوبر نگه داشته شد.

موقعیت حالت همدوس در صفحه مختلط (فضای باز) در میان مکان و تکانه یک نوسانگر کلاسیکی هم فاز θو هم دامنه (یا هم مقدار با میدان الکتریکی مختلط برای یک موج الکترو مغناطیسی) قرار می‌گیرد. همانطوریکه در شکل ۵ نشان داده شده‌است. عدم قطعیت، که به طور مساوی در همه جهت‌ها منتشر می‌شود، به وسیله یک دیسک با قطر ۲٫۱ نمایش داده می‌شود. از آنجایی که فاز افزایش می‌یابد و دیسک و مرکز دایره‌های حالت همدوس هیچ‌کدام نه پهن می‌شوند و نه کج. این شبیه‌ترین حالت کوانتومی ای است می‌تواند یک نقطه منفرد در فضای فاز باشد.

چون عدم قطعیت (و از اینرو نوفه اندازه‌گیری) در ${\frac {1}{2}}$ثابت باقی می‌ماند به طوریکه دامنه نوسانگر افزایش می‌یابد حالت خیلی شبیه یک موج سینوسی رفتار می‌کند، به صورت نشان داده شده در شکل ۱. و، از آنجاییکه حالت خلأ $|0>$، تنها حالت همدوس با $\alpha =0$ است، همه حالت‌های همدوس عدم قطعیت یکسانی دارند، مانند خلأ؛ بنابراین نوفه کوانتومی یک حالت همدوس را می‌توان به صورتی که ناشی از تغییرات خلأ باشد، تعبیر کرد.

(بهتر است ذکر شود که نماد گذاری $|\alpha |\,$ مربوط به یک حالت فوک نمی‌شود. برای نمونه، در $\alpha =1$، یک نباید با حالت فوک تک – فوتون اشتباه گرفته شود- که یک توزیع پواسونی حالت‌های عددی ثابت را با عدد فوتونی واحد میانگین نمایش می‌دهد)

حل فرمولی معادله ویژه مقداری حالت خلاء جایگزیده در یک موقعیت $\alpha \,$ در فضای فاز است، یعنی عملگر انتقال $D\left(\alpha \right)$ روی حالت خلأ عمل می‌کند:

$|\alpha >=e^{\left(\alpha {\hat {a}}^{\dagger }-\alpha ^{\star }{\hat {a}}\right)}|0>=D\left(\alpha \right)|0>$

این را می‌توان با استفاده از نمایش حالت همدوس در پایه حالت‌های فوک به سادگی دید، به طوریکه مجازاً همه نتایج با حالت‌های همدوس درگیر می‌شوند:

$|\alpha >=e^{-{\frac {|\alpha |^{2}}{2}}}\sum _{n=0}{\frac {\alpha ^{n}}{\sqrt {n!}}}|n>=e^{-{\frac {|\alpha |^{2}}{2}}}e^{{\hat {a}}{\hat {a}}^{\dagger }}|0>$

که $|n>$ها ویژه حالت‌های (عددی) هامیلتونی انرژی هستند؛ که یک توزیع پواسونی است. احتمال مشاهده n فوتون عبارتست از:

$P\left(n\right)=e^{-\left\langle n\right\rangle }{\frac {\left\langle n\right\rangle ^{n}}{n!}}$

به طور مشابه، عدد فوتونی میانگین در حالت همدوس $\left\langle n\right\rangle =\left\langle {\hat {a}}^{\dagger }{\hat {a}}\right\rangle =|\alpha |$ است و واریانس عبارت است از:

$\left(\Delta n\right)^{2}=Var\left({\hat {a}}^{\dagger }{\hat {a}}\right)=|\alpha |^{2}$

در محدوده بزرگ a این آمار مشاهده، با یک موج ایستای کلاسیکی به ازای همه مقادیر بزرگ a هم ارز است. این نتایج در آشکار سازی نتایج تنها یک آشکار ساز و بنابراین به همدوسی مرتبه اول وابسته است (نگاه کنید به درجه همدوسی). اگر چه، برای آشکار سازی همبستگی اندازه‌گیری‌ها با آشکار سازی‌های دامنه، همدوسی مرتبه بالا به کار می‌آید (به عنوان مثال، همبستگی شدت، همدوسی مرتبه دوم، با دو آشکار ساز). تعریف همدوسی کوانتومی گلاوبر به توابع هم بسته مرتبه n ام (همدوس مرتبه n ام) مر بوط می‌شود. به ازای همه nها حالت همدوس کامل همه مراتب n همبستگی مساوی با ۱ را داراست. به طور کامل برای همه مراتب همدوس است.

کار گلاوبر توسط نتایج هانبری– براون و توایس که الگوهای تداخلی مرتبه اول دور برد (صدها یا هزارها مایل) از طریق استفاده از نوسانات شدت (عدم همدوسی مرتبه دوم) که هر یک از آشکار سازها تولید کردند، برانگیخته شد یا تازه شد. (یکی، طی مدت بسیار کوتاهی – یک الگوی تداخلی تقریباً لحظه‌ای را از دو آشکار سازی می‌تواند ببیند، به علت فیلترهای باند باریک، که به صورت تصادفی به خاطر تغییر در اختلاف فاز نسبی می‌چرخند. با یک شمارشگر تطابقی الگوی تداخلی چرخنده، قویتر از زمان شدت افزوده شده، خواهد بود (معمولاً برای دو پرتو) و اینکه الگو قویتر از نویز پس زمینه خواهد بود. تقریباً همه اپتیک‌ها با همدوسی مرتبه اول سرو کار داشته‌است. نتایج هامبری – براون وترایس، گلابر را برای جستجوی همدوسی مراتب بالا برانگیخت، و او با یک توصیف کوانتوم – نظری همدوسی با همه مراتب در میدان الکترومغناطیسی (و یک توصیف کوانتوم – نظری نوفه + سیگنال) وارد شد؛ و عبارت «حالت همدوس» را ابداع کرد و نشان داد که آنها وقتی تولید می‌شوند که یک جریان الکتریکی کلاسیکی با میدان مغناطیسی برهم کنش داشته باشد.

درα≫۱ از شکل ۵، هندسه ساده به دست می‌دهد : $\Delta \theta |\alpha |={\frac {1}{2}}$ از این می‌تونیم بفهمیم که ارتباطی بین عدم قطعیت عدد و عدم قطعیت فاز وجود دارد ؛ $\Delta \theta \Delta n={\frac {1}{2}}$ که اغلب می‌توان به صورت رابطه عدم قطعیت فاز- عدد تعبیر کرد. این رابطه عدم قطعیت فرمولی نیست: هیچ عملگر فاز تعریف شده یکتا در مکانیک کوانتومی وجود ندارد. small

شکل ۴. احتمال آشکارسازی n فوتون، توزیع عددی فوتون، حالت همدوس در شکل ۳. به طوریکه لازم است برای یک توزیع پواسونی عدد فوتونی میانگین برابر باشد با واریانس توزیع عددی فوتون. میله‌ها مربوط به تئوری هستند و نقطه‌ها مربوط به مقادیر تجربی

شکل ۵. ترسیم فضایی فاز یک حالت همدوس. این شکل نشان می‌دهد که عدم قطعیت در حالت همدوس به طور مساوی در همه جهات توزیع شده‌است. محورهای افقی و قائم به ترتیب مربع‌ها ی X و P هستند. (متن را ببینید). نقاط قرمز روی محور X مرزهای نوفه کوانتومی در شکل ۱ را نشان می‌دهد.

ویژگی‌های ریاضیاتی

حالت همدوس همه ویژگی‌های خوب ریاضی یک حالت فوک را نمایش نمی‌دهد؛ برای نمونه دو حالت همدوس مختلف راست هنجار نیستند.

$<\beta |\alpha >=e^{-{\frac {1}{2}}\left(|\beta |^{2}+|\alpha |^{2}-2\beta ^{\star }\alpha \right)}\neq \delta \left(\alpha -\beta \right)$

بنابراین اگر نوسانگر در حالت کوانتومی$|\alpha >$ باشد و همچنین با احتمال غیر صفر در حالت کوانتومی دیگر$|\beta >$ باشد (اما حالت‌های دور از هم که در فضای فاز واقع می‌شوند، احتمال کمتری دارند). با این حال، از آنجا که آنها از رابطه همبستگی تبعیت می‌کنند تنها یک حالت می‌تواند به مجموعه حالت‌های همدوس تجزیه شود. از اینرو یک پایه فوق کامل را که می‌تواند به صورت قطری به هر حالت تجزیه شود تشکیل می‌دهند؛ و این بنیاد و اساس برای نمایش P سودارشان – گلاوبر است. این رابطه همبسته را می‌توان با کنش یکانی توضیح داد:

${\frac {1}{\pi }}\int |\alpha ><\alpha |d^{2}\alpha =1$

دشواری دیگراین است که$a^{\dagger }$ هیچ ویژه کتی ندارد (و$a$ هیچ ویژه برایی) معادله فرمولی زیر جانشین خوبی است و نتیجه خیلی مفیدی برای محاسبات تکنیکی دارد.

$a^{\dagger }|\alpha >=\left({\frac {\partial }{\partial \alpha }}+{\frac {\alpha ^{\star }}{2}}\right)|\alpha >$

آخرین حالت با عنوان حالت آگاروال شناخته شده‌است که به صورت $|\alpha ,1>$ نوشته می‌شوند. حالت‌های آگاروال برای مرتبه n را می‌توان به صورت زیر توضیح داد:

$|\alpha ,n>=\left(a^{\dagger }\right)^{n}|\alpha >$

حالت‌های همدوس چگالش بوز انیشتین

چگالش بوز-اینشتین (BEC) مجموعه‌ای از اتم‌های بوزونی است که همگی در حالت کوانتومی یکسانی هستند. در یک سیستم ترمودینامیکی، حالت پایه به صورت ماکروسکوپیکی، در زیر دمای بحرانی اشغال می‌شود -در این دما طول موج دوبروی بلندتر از فاصله بین اتمی تصور می‌شود. باور بر این است که ابرشارگی در هلیم۴- مایع به چگالش بوز- انیشتین در گاز ایده‌آل همبسته است. اما He-4 برهم کنش قوی‌ای دارد و عامل ساختار مایع (آمار مرتبه دوم) نقش مهمی را ایفا می‌کند. استفاده از حالت همدوس برای نمایش مولفه ابرشارگی هلیم۴-، تخمین خوبی از کسر (غیرچگالش/چگالش) را در ابرشارگی فراهم می‌کند و سازگار با نتایج پراکندگی نوترون‌های کند است. بیشتر ویژگی‌های خاص ابر شاره مستقیماًاز استفاده حالت همدوس در نمایش مولفه ابرشاره – که به صورت یک حالت تک ذره‌ای اشغال شده ماکروسکوپیکی با دامنه وفاز خوش تعریف روی حجم کامل عمل می‌کند- تبعیت می‌کند. (مولفه ابر شاره هلیم۴- از صفر در دمای گذار به ۱۰۰٪ در صفر مطلق می‌رود) اما کسر چگالی در دمای صفر مطلق حدود ۶٪ است و T=0 K.

در ابتدای مطالعه ابرشارگی، «پن روز» و «انساگر» متریک «متغیر مرتبه» ای برای ابرشارگی پیشنهاد کردندکه توسط یک مولفه عامل ماکروسکوپیکی (ویژه مقدار ماکروسکوپی) در مرتبه اول ماتریس پراکندگی کاهیده نمایش داده می‌شود. بعداً، سی.ان. یانگ اندازه‌گیری تعمیم یافته همدوسی کوانتومی ماکروسکوپی را پیشنهاد داد که «مرتبه دور – برد غیر قطری» نامیده می‌شد. ODLR، که شامل فرمیون و همچنین سیستمهای بوزونی است. ODLRO در هر زمانی که مولفه عامل مشترک بزرگ ماکروسکوپی (ویژه مقادیر) در ماتریس پراکندگی کاهیده مرتبه اول وجود داشته باشند، وجود دارد. ابرشارگی با یک مولفه عامل مشترک بزرگ در ماتریس پراکندگی مرتبه اول متناظر است. (و همه مراتب بالای ماتریس‌های پراکندگی کاهیده مانند هم رفتار می‌کنند). ابر رسانایی با مولفه عامل مشترک در ماتریس پراکندگی کاهیده مرتبه دوم (جفت الکترون کوپر) درگیر است.

مراتب ماتریس‌های پراکندگی کاهیده در توصیف ماکروسکوپی در ابر شاره‌ها ظاهراً مانند تابع‌های هم بستگی که در توصیف مراتب همدوسی تابش به کار می‌روند، هستند. هر دو نمونه‌های همدوسی کوانتومی ماکروسکوپی هستند. به طور ماکروسکوپی مولفه همدوسی بزرگ، به اضافه نوفه، در میدان الکترومغناطیسی توسط شرح سیگنال + نوفه گلاوبر داده می‌شود. ظاهراً همانند مولفه ابرشاره بزرگ ماکروسکوپی+ مولفه سیال طبیعی در مدل دو سیال ابرشارگی است.

لازم است ذکر شود که تابش الکترومغناطیسی همه روزه، مانند امواج رادیو وتلویزیون، نیز یک نمونه نزدیک به حالت‌های همدوس هستند. (همدوسی کوانتومی ماکروسکوپی). بهتر است «درنگ کنید» در موضوع علامت گذاری مرسوم بین کوانتوم و کلاسیک.

حالت‌های الکترون همدوس در ابررسانایی

الکترون‌ها فرمیون هستند، اما وقتی به صورت جفت‌های کوپر جفت می‌شوند مانند بوزون عمل می‌کنند و بنابراین می‌توانند یک حالت همدوس را در دمای پایین شکل دهند. چنین حالت‌های همدوسی جزئی از تبیین اثراتی مثل اثر هال کوانتومی نیمرساناهای ابررسانا در دما-پایین هستند.

تعمیم

در تئوری میدان کوانتومی و نظریه ریسمان، یک تعمیم از حالت‌های همدوس در مورد بینهایت درجه آزادی برای تعریف یک حالت خلأ با یک مقدار چشمداشتی خلأ متفاوت از خلأ اصلی استفاده می‌شود.

سیستم‌های کوانتومی بس ذره‌ای یک بعدی، درجات آزادی فرمیونی، حالت‌های برانگیخته انرژی پایین را می‌توان به صورت حالت‌های همدوس یک عملگر میدان بوزونی که برانگیختگی چاه-ذره را تولید می‌کنند، تقریب زد.

حالت‌های همدوس گاوسی مکانیک کوانتومی غیر نسبیتی را می‌توان به حالت‌های همدوس نسبیتی کلین_ گوردان و ذرات دیراک، تعمیم داد؛ نگاه کنید به جرالد کیاسر، فیزیک کوانتومی، نسبیت، و فضازمان مختلط (شمال- هلند ۱۹۹۰)

جستارهای وابسته

• نظریه میدان کوانتومی

اپتیک کوانتومی

میدان الکترومغناطیسی

درجه همدوسی

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Coherent state». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۳ فوریه ۲۰۱۴.