از ویکیپدیا، دانشنامهٔ آزاد
چندجملهای های لژاندر (Legendre polynomials) جوابهایِ معادله دیفرانسیل معمولی زیر موسوم به معادلهٔ دیفرانسیل لژاندر هستند:
d
d
x
[
(
1
−
x
2
)
d
d
x
P
n
(
x
)
]
+
n
(
n
+
1
)
P
n
(
x
)
=
0.
{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}
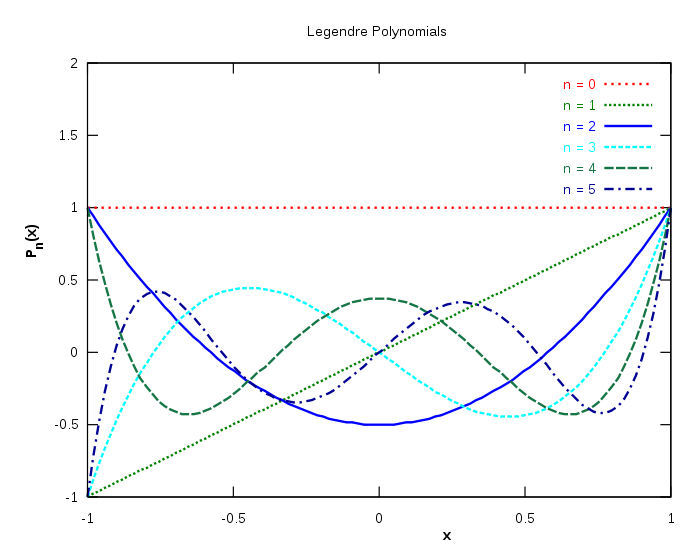
اولین چندجملهایهای لژاندر به صورت زیر هستند:
n
P
n
(
x
)
{\displaystyle P_{n}(x)\,}
0
1
{\displaystyle 1\,}
1
x
{\displaystyle x\,}
2
1
2
(
3
x
2
−
1
)
{\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}(3x^{2}-1)\,}
3
1
2
(
5
x
3
−
3
x
)
{\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}(5x^{3}-3x)\,}
4
1
8
(
35
x
4
−
30
x
2
+
3
)
{\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}(35x^{4}-30x^{2}+3)\,}
5
1
8
(
63
x
5
−
70
x
3
+
15
x
)
{\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}(63x^{5}-70x^{3}+15x)\,}
6
1
16
(
231
x
6
−
315
x
4
+
105
x
2
−
5
)
{\displaystyle {\begin{matrix}{\frac {1}{16}}\end{matrix}}(231x^{6}-315x^{4}+105x^{2}-5)\,}
7
1
16
(
429
x
7
−
693
x
5
+
315
x
3
−
35
x
)
{\displaystyle {\begin{matrix}{\frac {1}{16}}\end{matrix}}(429x^{7}-693x^{5}+315x^{3}-35x)\,}
8
1
128
(
6435
x
8
−
12012
x
6
+
6930
x
4
−
1260
x
2
+
35
)
{\displaystyle {\begin{matrix}{\frac {1}{128}}\end{matrix}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)\,}
9
1
128
(
12155
x
9
−
25740
x
7
+
18018
x
5
−
4620
x
3
+
315
x
)
{\displaystyle {\begin{matrix}{\frac {1}{128}}\end{matrix}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)\,}
10
1
256
(
46189
x
10
−
109395
x
8
+
90090
x
6
−
30030
x
4
+
3465
x
2
−
63
)
{\displaystyle {\begin{matrix}{\frac {1}{256}}\end{matrix}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)\,}
پیوند به بیرون [ ویرایش ]
Abramowitz, Milton & Stegun, Irene A., eds. (1965), “Chapter 8”, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, ISBN 0-486-61272-4 See also chapter 22.

![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd51c7228067db4bea119843fb19c6caab834954)











