معادله موج الکترومغناطیس
معادله موج الکترومغناطیس دومین حکم دیفرانسیل جزئی معادله است که انتشار موجهای الکترومغناطیس را در محیط مادی یا خلاء توصیف میکند. فرم همگن این معادله به هر دو شکل میدان الکتریکی E و میدان مغناطیسی B نوشته میشود:
در اینجا سرعت نور است ²∇ عملگر لاپلاس است. در خلاء c = c0 = 299,792,458 متر بر ثانیه است. معادله موج الکترومغناطیس از معادله ماکسول پیروی میکند. باید به این نکته توجه کرد که در متون گذشته B چگالی جریان مغناطیسی یا القای مغناطیسی نامیده میشد.
منشاء معادله موج الکترومغناطیسی[ویرایش]
توزیع بار[ویرایش]
توزیع بار نیازمند آن است که زمان سرعت تغییرات بار کل در یک حجم V با جریان خالص جاری در سطح بسته s برابر باشد:
در اینجا J چگالی خالص (آمپر بر مترمربع) جریان در سطح بسته و ρ چگالی شارژ (کولن بر متر مکعب) در هر نقطه از حجم است. طبق قضیه دیورژانس این رابطه میتواند از فرم انتگرالی به دیفرانسیلی تبدیل شود.
قانون قبلی مداری آمپر به تصحیح ماکسول در شکل اصلی آن، قانون مداری آمپر با میدان مغناطیسی B بواسطه J رابطه دارد:
در اینجا S یک سطح باز محدود شده در خط منحنی C است. این شکل انتگرالی با بکار بردن قضیه استوکس میتواند به شکل دیفرانسیلی تبدیل شود:
تناقض بین قانون مداری آمپر و قانون توزیع بار: با گرفتن دیورژانس از هر دو طرف قانون مداری آمپر داریم:
دیورژانس کرل هر میدان برداری، شامل میدان مغناطیسی B همیشه برابر صفر است:
با بهم پیوستن این دو معادله داریم:
زیرا یک ثابت غیر صفر است. پس به این ترتیب
بههرحال با توجه به قانون توزیع بار داریم:
بنابراین، همانند قانون مداری کیرشهف، قانون مداری آمپر تنها برای حفظ وضعیت درگیر چگالی بار ثابت باید پدیدار شود. (نباید مانند وضعیتی که در شارژ و دشارژ صفحه خازن رخ میدهد، باشد.)
تصحیح قانون مداری آمپر توسط ماکسول[ویرایش]
ماکسول تصور میکرد که برقراری جریان در اتصال با قطبش خطی یک دی الکتریک است. توجیه این بسط واقعی جابجایی جریان چنانچه در زیر آمده؛ شرح قانون گاوس در شکل انتگرالی:
در اینجا S سطح بسته در حجم V است. با بکار بردن قضیه دیورژانس این شکل انتگرالی میتواند بهشکل دیفرانسیلی تبدیل شود:
با مشتقگیری زمانی از هر دو طرف معادله و معکوس کردن دیفرانسیل در سمت چپ داریم:
نتیجهگیری اخیر، در ادامه قانون مداری آمپر و معادله توزیع بار اظهار میکند که اینجا دواصل میدان مغناطیسی عملی است. چگالی جریان J که آمپر بنا نهاد، و جریان:
بنابر شکل درست و تصحیح شده قانون مداری آمپر، داریم:
فرضیه ماکسول مبنی بر اینکه نور یک موج الکترومغناطیس است[ویرایش]

مقاله ۱۸۶۴ ماکسول نظریه الکترودینامیک میدان الکترومغناطیسی عنوان گرفت. وی قانون مداری آمپر را که قسمت سوم مقاله ۱۸۶۱ اش، در مورد خطوط (میدان) نیرو بود، به شکل اصلاح شده بکار برد.قسمت چهارم از مقاله اش نظریه الکترومغناطیس نور نامیده شد. ماکسول تغییر جریان را با چند معادله دیگر الکترومغناطیس ترکیب کرد و یک معادله موج با سرعت برابر با سرعت نور بدست آورد. او معتقد بود: این نتیجه برای نشان دادن اینکه نور و مغناطیس خاصیتهای مواد مشابه هستند، ظاهر میشود. و نور بنا بر قوانین الکترومغناطیس، یک اختلال الکترومغناطیسی منتشر شده در یک میدان است. استنتاج ماکسول از معادله موج الکترومغناطیس، در فیزیک جدید با روشهای سادهتر، با نسخه تصحیح شده قانون مداری آمپر که با قانون القای فارادی ترکیب میشود، جایگزین شده بود. برای بدست آوردن معادله موج الکترومغناطیس در خلاء این روشهای مدرن بکار میروند.
در اینجا ρ = 0 است، چون چگالی بار وجود ندارد. با کرل گرفتن از معادلات کرل، داریم:
با بکارگیری اتحاد برداری
(در اینجا V هر تابع برداری در فضاست، که معادله را به معادله موج تبدیل میکند.
در اینجا متر بر ثانیه سرعت نور است.
شکل هموردای معادله موج همگن[ویرایش]

معادلات نسبیت میتوانند به شکل هموردا نوشته شوند:
این همان چهار بردار پتانسیل است:
با توجه به شرط لورنتس:
- .
در اینجا
عملگر دالامبر است. (مربع خطای تایپی نیست؛ این یک نماد درست برای این عملگر است.)
معادله موج همگن در دستگاه چهار بعدی منحنی[ویرایش]
معادلات ماکسول در چهار بعد معادلات موج الکترومغناطیس از دو راه اصلاح شده اند؛ مشتق جایگزین شده با مشتق هموردا، و روش نوین که وابسته به پدیدار شدن انحناست.
در اینجا تانسور خمش ریچی، و ; نمایانگر دیفرانسیل هموردا است. عمومیت دادن شزط لورنتس در دستگاه چهار بعدی منحنی به اینصورت فرض میشود:
- .
معادله موج الکترومغناطیس ناهمگن[ویرایش]
معادله موج الکترومغناطیس ناهمگن بار نقطهای متغیر در واحد زمان، و چگالی جریان میتواند مانند یک چشمه موج الکترومغناطیس در خلاء عمل کند. معادله ماکسول میتواند به فرم معادله موج با چشمهها نوشته شود. افزودن چشمهها به معاله موج، معادلات دیفرانسیل جزئی ناهمگن میسازد.
حل معادله موج الکترومغناطیس[ویرایش]
معادله موج راه حل اصلی برای معادله موج الکترومغناطیس یک وضعیت خوب خطی از موجها به شکل
و
است. درواقع تابع g در استدلال بدون مقدار φ، خوب عمل میکند. در اینجا فرکانس زاویهای (رادیان بر ثانیه) و بردار موج است (رادیان بر متر). اگرچه تابع g میتواند وجود داشته باشد و اغلب یک موج سینوسی تک رنگ است، نباید سینوسی یا حتی دورهای باشد. در عمل g نمیتواند دوره تناوب نامحدود داشته باشد، چون هر موج الکترومغناطیس واقعی باید همیشه یک اندازه محدود در فضا و زمان داشته باشد. بنابراین، و بر اساس نظریه تجزیه فوریه، یک موج واقعی باید ترکیبی باشد از موقعیت خوب یک سیستم نامحدود با فرکانس سینوسی. بعلاوه، به عنوان یک راه حل معتبر، بردارهای موج و فرکانس زاویهای مستقل نیستند؛ آنها باید به رابطه انتشار مرتبط باشند:
در اینجا K عدد موج و λ طول موج است.
وضعیت ثابت سینوسی تک رنگ[ویرایش]
سادهترین روش حل معادله موج از فرض کردن یک موج سینوسی تک فرکانس در حالت تفکیک پذیر آن بدست میآید:
- در اینجا عدد موهومی است.
- فرکانس زاویهای است(رادیان بر ثانیه).
- فرکانس است(هرتز).
- و فرمول لئونارد اویلر است.
حل موج تخت[ویرایش]
حل موج تخت سینوسی از معادله موج الکترومغناطیس یک صفحه و یک بردار نرمال تعریف میشود:
- .
حل موج رونده عرضی با معادله موج، به این صورت است:
و
در اینجا : یک بردار مکان است(متر). این روش حل بیان میکند موج عرضی در جهت بردار نرمال میرود. اگر یک جهت Z، مثل جهت و یک جهت X مثل جهت تعریف کنیم، طبق قانون فارادی، خطوط میدان مغناطیسی در جهت y است و با رابطه به میدان الکتریکی وابسته میشود. چون دیورژانس میدان الکتریکی و مغناطیسی صفر است، در جهت انتشار، میدان وجود ندارد. این روش حل، حل قطبش خطی معادله موج است. در اینجا حل قطبش کروی در هر میدان چرخان حول بردار نرمال هم وجود دارد.
تجزیه طیفی[ویرایش]
چون معادلات ماکسول در خلاء، خطی حل میشوند، میتوان آنها را به موقعیتهای خوب سینوسی تجزیه کرد. این اساس روش تبدیلات فوریه برای حل معادله دیفرانسیل است. با حل سینوسی معادله موج الکترومغناطیس، داریم:
و
در اینجا : زمان(ثانیه)،
- فرکانس زاویه ای(رادیان بر ثانیه)،
- بردار موج(رادیان بر متر)،
و : زاویه فاز(رادیان) است. بردار موج با رابطه
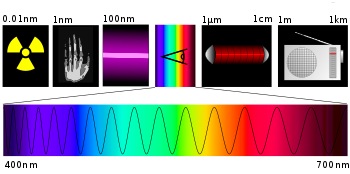
به فرکانس زاویهای وابسته است. در اینجا k عدد موج و λ طول موج است. طیف الکترومغناطیس، همچون تابع طول موج، یک طرح از بزرگی میدان (یا انرژی) است.
سایر روشها[ویرایش]
حل تحلیلی تقارن کروی یا استوانهای معادله موج الکترومغناطیس نیز امکانپذیر است. در مختصات استوانهای معادله موج میتواند به این صورت نوشته شود:
- ،
و
- .
این معادلات میتوانند به شکل تابع بسل در مختصات کروی بازنویسی شوند. در مختصات استوانه ای، حل معادله موج، تابع بسل معمولی عددی است.
سایر موارد[ویرایش]
نظریه و آزمایش[ویرایش]
کاربردها[ویرایش]
منابع[ویرایش]
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
بیشتر بخوانید[ویرایش]
Electromagnetism[ویرایش]
Journal articles[ویرایش]
- Maxwell, James Clerk, "A Dynamical Theory of the Electromagnetic Field", Philosophical Transactions of the Royal Society of London 155, 459-512 (1865). (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
Undergraduate-level textbooks[ویرایش]
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8.
- Edward M. Purcell, Electricity and Magnetism (McGraw-Hill, New York, 1985). ISBN 0-07-004908-4.
- Hermann A. Haus and James R. Melcher, Electromagnetic Fields and Energy (Prentice-Hall, 1989) ISBN 0-13-249020-X.
- Banesh Hoffmann, Relativity and Its Roots (Freeman, New York, 1983). ISBN 0-7167-1478-7.
- David H. Staelin, Ann W. Morgenthaler, and Jin Au Kong, Electromagnetic Waves (Prentice-Hall, 1994) ISBN 0-13-225871-4.
- Charles F. Stevens, The Six Core Theories of Modern Physics, (MIT Press, 1995) ISBN 0-262-69188-4.
- Markus Zahn, Electromagnetic Field Theory: a problem solving approach, (John Wiley & Sons, 1979) ISBN 0-471-02198-9
Graduate-level textbooks[ویرایش]
- Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X.
- Landau, L. D., The Classical Theory of Fields (Course of Theoretical Physics: Volume 2), (Butterworth-Heinemann: Oxford, 1987). ISBN 0-08-018176-7.
- Maxwell, James C. (1954). A Treatise on Electricity and Magnetism. Dover. ISBN 0-486-60637-6.
- Charles W. Misner, Kip S. Thorne, جان ویلر, Gravitation, (1970) W.H. Freeman, New York; ISBN 0-7167-0344-0. (Provides a treatment of Maxwell's equations in terms of differential forms.)
Vector calculus[ویرایش]
- P. C. Matthews Vector Calculus, Springer 1998, ISBN 3-540-76180-2
- H. M. Schey, Div Grad Curl and all that: An informal text on vector calculus, 4th edition (W. W. Norton & Company, 2005) ISBN 0-393-92516-1.



















































