۰٫۹۹۹…
در ریاضیات، ۰٫۹۹۹… (که با علامتهایی مانند یا نیز نمایش مییابد) یک عدد اعشاری متناوب از نوع ساده متشکل از تعداد بینهایت ۹ بعد از ممیز را نشان میدهد. این عدد برابر با عدد یک است. به عبارتی دیگر، "۰٫۹۹۹…" و "۱" عددی یکسان را نشان میدهند. شیوههای متنوعی برای اثبات این برابری با درجات مختلفی از دقت ریاضی وجود دارد. هر عدد اعشاری مختوم غیر صفر، با یک عدد اعشاری متناوب دوقلوی خود برابر است که میتوان آن را با بینهایت ۹ نشان داد (برای مثال ۸٫۳۲ برابر است با ۸٫۳۱۹۹۹…). تقریباً، همواره عدد اعشاری مختوم ترجیح داده میشود، که این موضوع به افزایش این تصور غلط که تنها شکل نمایش همان عدد مختوم است، دامن میزند. چنین مفهومی در تمام مبناهای دیگر (با بزرگترین عدد ممکن)، یا اعداد حقیقی مشابه وجود دارد. تساوی ۰٫۹۹۹… و عدد ۱ به نبود مقادیر غیر صفر بینهایت کوچک در سیستم اعداد حقیقی مربوط میشود؛ این سیستم رایجترین سیستم در آنالیز ریاضی است. برخی سیستم اعداد جایگزین، مانند اعداد فراحقیقی شامل مقادیر بسیار کوچک غیر صفر نیز میباشند. در بسیاری از این سیستمها، مفهوم ۰٫۹۹۹… معادل عدد یک است، اما در برخی از این سیستمها، حتی بینهایت ۹ نیز همواره اندکی کوچکتر از مقدار ۱ میباشد.
معادله ۰٫۹۹۹…=۱ مدتهاست که توسط ریاضیدانان پذیرفته و به بخشی از دانش ریاضی تبدیل شدهاست. با این وجود، برخی افراد آن را غیرعادی مییابند، دربارهٔ آن سؤال میپرسند و حتی آن را رد میکنند. این مسئله موجب انجام برخی پژوهشها در آموزش ریاضی پیرامون این موضوع شدهاست.
اثبات جبری[ویرایش]
اثبات جبری، برای نشان دادن تساوی ۰٫۹۹۹… و ۱، از مفاهیمی مانند کسر، تقسیم زیرهم و دستکاری عددی استفاده میکند تا تغییراتی ایجاد کند که تساوی ۰٫۹۹۹ و ۱ دستنخورده باقی بماند. با این وجود، این اثبات خیلی دقیق نیست، زیرا شامل توصیف تحلیلی دقیق ۰٫۹۹۹… نمیباشد.
کسر و تقسیم طولانی[ویرایش]
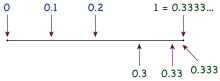
یکی از دلایلی که اعداد اعشاری متناوب یک شکل گسترشیافته اعداد اعشاری مختومند، نشاندادن کسرها میباشد. استفاده از تقسیم طولانی، یعنی تقسیم ساده اعداد صحیحی مانند ۱⁄۹ 1⁄9 عدد تناوبی ۰٫۱۱۱… را حاصل میکند که در آن، ارقام بدون پایان، تکرار میشوند. این اعداد اعشاری یک اثبات سریع برای ۰٫۹۹۹…=۱ را ثمر میدهد. ضرب عدد ۱ در ۹، برابر ۹ است، لذا ۹ ×۰٫۱۱۱… برابر ۰٫۹۹۹… و 9 × 1⁄9 برابر ۱ است، لذا ۰٫۹۹۹…=۱.
یک شکل دیگر اثبات این اثبات ضرب 1⁄3= ۰٫۳۳۳… در ۳ است.
دستکاری عددی ( جای گذاری با متغیر ها )[ویرایش]
زمانی که عددی اعشاری در ۱۰ ضرب میشود، ممیز عدد یک رقم به سمت چپ حرکت میکند؛ لذا حاصلضرب ۱۰ و ۰٫۹۹۹… برابر است با ۹٫۹۹۹…، که ۹ رقم بزرگتر از عدد اصلیست. برای دیدن این، در نظر بگیرید که در تفریق ۰٫۹۹۹… از ۹٫۹۹۹ هر یک از ۹ها با یک ۹ دیگر خنثی میشود. مرحله آخر در جبر به این شرح است:
بحث[ویرایش]
اگرچه این اثباتها نشان میدهند که ۰٫۹۹۹…=۱ است، اندازه این برابری به درک مخاطب بستگی دارد. در حساب مقدماتی، این اثباتها به توضیح اینکه چرا ۰٫۹۹۹…=۱ ولی ۰٫۳۳۳…<0.۴، کمک میکند. در جبر مقدماتی، این اثبات به توصیف علت جوابدادن روش عمومی تبدیل کسر به عدد اعشاری متناوب و برعکس، کمک میکند. این اثبات به درک ارتباط اساسی اعداد اعشاری و ارقامی که نشان میدهند، کمک میکند، تا پاسخ این سؤال که دو عدد مختلف چگونه میتوانند یکسان باشند، یافته شود.[۱]
زمانی که یک طرح نشاندادن توصیف میشود، میتوان برای توجیه قوانین حساب اعشاری استفاده شده در اثباتهای بالا، از آن استفاده کرد. به علاوه، میتوان بهطور مستقیم نشان داد که اعداد اعشاری ۰٫۹۹۹… و ۱٫۰۰۰… یک عدد حقیقی یکسان را نمایش میدهند؛ این در تعریف نیز وارد شدهاست. در پایین میتوان آن را مشاهده کرد
اثبات تحلیلی[ویرایش]
از آنجا که مسئله ۰٫۹۹۹… در پیشرفت رایج ریاضی نقشی ندارد، میتوان اثبات آن را به عهده قضایای استاندارد آنالیز حقیقی موکول کرد. نیاز ما مشخص کردن اعداد حقیقی است که میتوان به شکل اعشار نشان داد، که شامل یک علامت اختیاری، دنباله محدودی از اعداد که جزء صحیح آن را نمایش میدهند، یک علامت اعشار، و دنبالهای از اعداد که بخش اعشاری را نشان میدهند. برای عدد ۰٫۹۹۹… بخش صحیح را با عبارت b0 نشان میدهند، که این عدد میتواند منفی نیز باشد، شکل کلی آن به صورت زیر است:
باید توجه کرد که بخش اعشاری بر خلاف بخش صحیح، به تعداد پایانپذیری از اعداد محدود نمیشود. این همان نمایش مکانی است، برای مثال عدد ۵ در ۵۰۰، ارزش ده برابر عدد ۵ در ۵۰ دارد، و همچنین عدد ۵ در ۰٫۰۵ یک دهم عدد ۵ در ۰٫۵ ارزش دارد.
سریها و دنبالههای نامتناهی[ویرایش]
شاید رایجترین توسعه استفاده از اعداد اعشاری گسترده، توصیف آنها به عنوان مجموعی از سریهای نامتناهی است. در حالت کلی:
برای عدد ۰٫۹۹۹… زمانی میتوان از قضیه سری همگرا دربارهٔ سری هندسی استفاده کرد که:[۲]
اگر آنگاه
از آنجا که این سری چنینی سری با ضریب r=1⁄10 میباشد، این قضیه حل این مسئله کاربرد دارد:
اثبات این قضیه در سال ۱۷۷۰ در کتاب عناصر جبر لئونارد اویلر بیان شدهاست.[۳]
موضوع مجموع سریهای هندسی حتی به قبل از اویلر باز میگردد. در قرن ۱۸ام، اثباتی دیگر مشابه اثبات جبری آمده ذکر شده در بالا ارائه شد و در سال ۱۸۱۱، رد کتاب معرفی جبر، با استفاده از سریهای هندسی، مانور مشابهی روی عدد ۰٫۹۹۹ انجام شد.[۴] عکسالعملهای قرن ۱۹ ام، مانند روشهای جمعکردن آزادانه سبب ایجاد توصیفی شد که امروزه نیز به کار میرود: مجموع سری را میتوان با حد دنباله و مجموع اعداد جزئی آن توصیف کرد. اثبات مربوطه این قضیه صراحتاً آن دنباله را محاسبه میکند؛ میتوان آن را در هر کتاب حساب و آنالیزی یافت.[۵]
یک دنباله (x0, x1, x2, ...) دارای حد x است، اگر اندازه |x − xn| با افزایش n کاهش یابد. این بیان که ۰٫۹۹۹…=۱ است را میتوان با حد دنباله نشانداد:[۶]
آخرین قدم که، با ∞ → n به 1⁄10n → ۰، با توجه به خاصیت ارشمیدسی اعداد حقیقی قابل توجیه است. این گرایش بر پایه حد عدد ۰٫۹۹۹… دقت کمی دارد. برای مثال، کتاب حساب دانشگاهی در سال ۱۸۴۶، توضیح میدهد که «۰٫۹۹۹ +، تا بینهایت=۱ است زیرا هر انضمامی از ۹ سبب میشود مقدار به ۱ نزدیکتر شود»؛ حساب مدارس در سال ۱۸۹۵ میگوید «... زمانی که تعداد زیادی ۹، در کنار هم قرار میگیرند، تفاوت بین ۱ و ۰٫۹۹۹۹۹… بهطور غیرقابل باوری کم است.»[۷] این اکتشافات سبب میشود دانشآموزان گمان کنند ۰٫۹۹۹… کمتر از ۱ است.
بازههای تودرتو و کمترین کران بالا[ویرایش]
توصیف سریها در بالا راهی ساده برای توصیف اعداد حقیقی است که بسط اعشاری دارند. یک روش مکمل برای فرایند مخالف مناسب است: میتوان یک عدد حقیقی را با یک بسط اعشاری توصیف کرد تا آن را نامگذاری نمود.
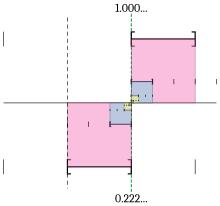
اگر یک عدد حقیقی مانند x در بازه بسته [۰, ۱۰] (اعداد بزرگتر مساوی ۰ و کوچکتر مساوی ۱۰) قرار داشته باشد، میتوان این بازه را به ده بازه مساوی شامل [۰, ۱]، [۱, ۲]، [۲, ۳]، ... و [۹, ۱۰] تقسیم کرد. عدد x به یکی از این بازهها تعلق دارد. اگر مثلاً این عدد به بازه [۲, ۳] تعلق داشته باشد، میتوان آن بازه را نیز بهطور مشابه به ده بازه شامل [۲, ۲٫۱]، [۲٫۱, ۲٫۲]، ... و [۲٫۹, ۳] تقسیم کرد. با ادامه این فرایند یک دنباله نامتناهی از بازههای تودرتو ظاهر میشود که برچسب ارقام دنباله نامتناهی شامل b0, b1, b2, b3, ... را میگیرد و میتوان نوشت
در این قاعده، اینکه ۰٫۹۹۹…=۱ و ۱٫۰۰۰…=۱ است به ترتیب این حقایق را نشان میدهند که ۱ در هر دو بازه [۰, ۱] و [۱, ۲] قرار دارد، لذا میتوان در زمان یافتن ارقام آن، از زیر بازههای نیز استفاده کرد. برای اطمینان از اینکه این مفهوم از علامت "=" سو استفاده نمیکند، نیاز به از نوساختن عدد حقیقی منحصر به فرد برای هر عدد اعشاری است. میتوان آن را با حدها انجام داد، اما سایر ساختمانها از این موضوع تبعیت میکنند.[۸]
یک انتخاب سرراست، قضیه بازههای تودرتو است، که ضمانت میکند، دنبالهای از بازههای تودرتو و بسته، که طولشان بهطور دلخواه کوچک میشود، در یک عدد حقیقی اشتراک دارند؛ لذا b0.b1b2b3… به این شکل توصیف میشود که معادل عددی است که بین تمام بازههای [b0, b0 + 1], [b0.b1, b0.b1 + 0.1] و الی آخر، مشترک است؛ لذا ۰٫۹۹۹… عدد حقیقی منحصر به فردی است که در تمام بازههای [۰, ۱]، [۰٫۹, ۱]، [۰٫۹۹, ۱]، [۰٫۹۹...۹, ۱] قرار دارد. از آنجا که یک تنها عنصری است که در تمام این بازهها وجود دارد، ۰٫۹۹۹…=۱ میباشد.[۹]
قضیه بازههای تودرتو، بر فراز یک ویژگی اساسیتر اعداد حقیقی یافت میشود: وجود کوچکترین کران بالا یا سوپریمم. طبق تعریف، b0.b1b2b3… کوچکترین کران بالای مجموعه اعداد {b0, b0.b1, b0.b1b2, ...} است.[۱۰] میتوان نشان داد این تعریف با رویه تقسیمبازهها نامتناقض است و بر ۰٫۹۹۹…=۱ دلالت دارد. تام آپوستول بحث میکند،
این حقیقت که یک عدد حقیقی را میتوان به دو شکل اعشاری نشان داد با این حقیقت در ارتباط است که دو مجموعه مختلف از اعداد حقیقی قادرند سوپریمم یکسانی داشته باشند.[۱۱]
اثبات از طریق ساختار اعداد حقیقی[ویرایش]
برخی روشها به صراحت توصیف میکنند که اعداد حقیقی با توجه به نظریه مجموعهها ساختمانهایی ویژ] بر اساس اعداد گویا هستند. اعداد طبیعی (شامل ا، ۲، ۳، و ...) از یک شروع میشوند و ادامه مییابند، لذا هر عددی یک جفت مخالف دارد. اگر به همراه هر عدد طبیعی، عدد منفی آن را نیز بیاوریم، با در نظر گرفتن صفر، میتوان مجموعه اعداد صحیح را تعریف کرد. با تقسیم این مقادیر به مقادیر صحیح دیگر، میتوان اعداد گویا را معرفی نمود. این اعداد را میتوان با ۴ عمل اصلی جمع، تفریق، ضرب و تقسیم همراهی کرد. بهطور علمیتر، اینها دارای نظم هستند، لذا میتوان اعداد را به یکدیگر مقایسه کرد و مشخص نمود که بزرگتر، کوچکتر و هم اندازه همند.
قدمگذاری از اعداد گویا به حقیقی توسعهای اصلی است. حداقل دو راه مشهور برای رسیدن به قدم وجود دارد که هر دو در سال۱۸۷۲ چاپشدهاند: برش ددکیند و دنباله کوشی. اثباتهای ۰٫۹۹۹…=۱ از این ساختارها استفاده میکند، در کتابهای آنالیز حقیقی یافت نمیشود، درحالی که تمایل مدرن در دهههای اخیر به استفاده از آنالیز بدیهی بودهاست. حتی زمانی که ساختاری پیشنهاد میشود، اغلب برای بدیهی بودن اعداد حقیقی به کار میرود، که سپس اثبات بالا را پشتیبانی میکند. اما، برخی نویسندگان بیان میکنند که شروع با یک ساختار، متناسب است، و اثباتهای حاصل خودکفایند.[۱۲]
برش ددکیند[ویرایش]
در برش ددکیند، هر عدد حقیقی مانند x با مجموعه نامتناهی اعداد گویای کوچکتر از x نمایش داده میشود.[۱۳] به ویژه، عدد حقیقی ۱، مجموعهای از تمام اعداد گویا است که کمتر از ۱اند.[۱۴] هر بسط اعشاری یک برش ددکیند را مشخص میکند: مجموعهای از اعداد گویا که کمتر از برخی مراحل توسعهاند؛ لذا عدد حقیقی ۰٫۹۹۹… مجموعهای از اعداد گویا مانند r است که r<0، یا r<0.9، یا r<0.99، یا rهای کمتر از برخی اعداد دیگرند که به شکل زیر میباشند:
هر عنصری از ۰٫۹۹۹… کوچکتر از ۱ است لذا عنصری از عدد حقیقی ۱ میباشد. برعکس، عنصر ۱ یک عدد گویا است.
که بر این دلالت دارد که
از آنجا که اعداد ۰٫۹۹۹… و ۱ مجموعه اعداد گویای یکسانی دارند، این دو عدد برابرند: ۰٫۹۹۹…=۱.
این توصیف اعداد حقیقی به عنوان برشهای ددکیند اولینبار در سال ۱۸۷۲ توسط ریچارد ددکند مطرح شد.[۱۶] روش بالا برای تعیینکردن بسط اعشاری یک عدد حقیقی در مقالهای به عنوان "آیا ۰٫۹۹۹…=۱ است؟" توسط فرد ریچمن، در مجله ریاضیات مطرح شد،[۱۷] که هدف آن آموزش به استادان دانشگاهی ریاضی و شاگردان آنها بود.[۱۸] ریچمن اشاره میکند که استفاده از برشهای ددکیند در هر زیرمجموعه متراکم از اعداد حقیقی، نتایجی یکسان به ثمر خواهد رساند؛ به ویژه، او برای نشان دادن بدیهیتر بودن یکی از اثباتها از کسر اعشاری استفاده میکند. او همچنین اشاره دارد این تعریف اجازه میدهد {x:x<1} به وسیله {x:x≤۱} برش نیابد. «چرا این کا ر را انجام دهیم؟ دقیقاً برای اینکه وجود اعداد متمایز ۰٫۹۹۹… و ۱ را نشان دهیم؛ لذا میبینیم که در توصیف سنتی اعداد حقیقی معادله ۰٫۹۹۹…=۱ در ابتدا به کار میرود.»[۱۹] اصلاح دیگری از این رویه به ساختار متفاوتی هدایت میکند که ایندو برابر نیستند. اگرچه آن نامتناقض است، بسیاری از قوانین رایج حساب اعشاری دیگر اعتباری ندارند، برای مثال کسر 1⁄3 هیچ نمایش عددی ندارد، سیستمهای عددی جایگزین را در پایین ببینید.
دنباله کوشی[ویرایش]
یکی دیگر توصیفات یک عدد حقیقی استفاده از حد دنباله کوشی برای اعداد گویاست. این ساختار اعداد حقیقی، بهطور غیرمستقیم از ترتیب اعداد گویا استفاده میکند. ابتدا فاصله بین x و y، به صورت |x-y| محاسبه میشود، منظور از |z|، بزرگترین مقدار z و −z است، لذا همواره مثبت میباشد. سپس اعداد حقیقی به عنوان دنبالهای از اعداد گویا تعریف میشوند که با استفاده از این فاصله دارای ویژگیهای دنباله کوشی میباشند. در دنباله (x0, x1, x2, ...)، نقشهای از اعداد طبیعی به گویا، برای هر عدد گویای δ یک N وجود دارد که برای هر m و n کوچکتر از N |xm − xn| ≤ δ. (فاصله بین عبارات از هر عدد گویای مثبتی کوچکتر میشود)[۲۰]
اگر (xn) و (yn) دو دنباله کوشی باشند، آنها معادل اعداد حقیقی توصیف میشوند اگر حد دنباله (xn − yn)، صفر باشد. کوتاهسازی عدد اعشاری b0.b1b2b3... دنبالهای از اعداد گویا را ایجاد میکند که کوشی است؛ میتوان با استفاده از آن ارزش واقعی عدد را مشخص کرد.[۲۱] لذا در این حالت باید دنباله اعداد گویا را نشان داد:
حد این دنباله صفر است؛ لذا میتوان نشان داد:
اگر کسی با حد دنبالهها آشنایی داشته باشد، این حد را به سادگی درک میکند.[۲۲] لذا ۰٫۹۹۹…=۱.
اولین بار این توصیف در سال ۱۸۷۲ و توسط ادوارد هاینه و گئورگ کانتور ارائه شد.[۱۶] روش مطرح شده دربارهٔ بسط اعشاری، شامل تساوی ۰٫۹۹۹…=۱، در کتاب ریاضی کلاسیک: یک تفسیر معاصر، از گریفیتز و هیلتون در سال ۱۹۷۰ چاپ شد. در این کتاب نگاهی جدید به این مفهوم شدهاست.[۲۳]
نمایش اعشاری نامتناهی[ویرایش]
معمولاً در آموزش متوسطه ریاضیات، یک عدد حقیقی را به صورت ترکیبی از یک عدد صحیح، علامت ممیز، و یک دنباله نامتناهی نشان میدهند که این بخش، قسمت اعشاری آن را نمایان میسازد. در این ساختار، مجموعه اعداد صحیح بعد ممیز مجموعه از اعداد حقیقیاند. این ساختار میتواند بعد از بیان یک رابطه همارزی برای مجموعهای که نشان میدهد ۰٫۹۹۹…=۱، به شکل دقیقی مخاطب را راضی کند.[۲۴]
تعمیم[ویرایش]
۰٫۹۹۹…=۱ به دو روش تعمیم مییابد. ابتدا برای اعداد غیر صفر با بخش اعشاری متناهی (با ۰های پایانپذیر) یک همتا با ۹های پایان ناپذیر وجود دارد. برای مثال ۰٫۲۴۹۹۹… همارز ۰٫۲۵ است. این اعداد دقیقاً کسرهای اعشاریاند.[۲۵]
ثانیاً، در هر مبنا، یک قضیه قابلمقایسه ایجاد میشود. برای مثال در مبنای ۲ (دستگاه اعداد دودویی) ۰٫۱۱۱… معادل ۱ است، و در مبنای ۳، ۰٫۲۲۲… معادل ۱ میباشد. کتابهای درسی آنالیز حقیقی از مثال ۰٫۹۹۹… عبور میکنند و یک یا هردوی این تعمیمها را از ابتدا فراهم میآورند.[۲۶]
نمایشهای جایگزین ۱، در مبناهای غیر صحیح نیز رایج است. در مبنای نسبت طلایی دو شکل استاندارد نمایش عبارتند از ۱٫۰۰۰… و ۰٫۱۰۱۰۱۰…، و نمایشهای فراوانی وجود دارند که شامل ۱های همسایه میشوند. بهطور کلی، برای تمام qهای بین ۱ و ۲، بسطهای غیرقابل شمارشی از مبنای q برای ۱ وجود دارد. از طرف دیگر، هنوز qهای فراوانی وجود دارند (شامل تمام اعداد طبیعی بزرگتر از ۱) که به جز ۱٫۰۰۰…، تنها یک بسط در مبنای q برای یک دارند. اولین بار، پل اردیش، میکلوس هارواس، و استوان جو، در حدود سال ۱۹۹۰، این نتایج را آشکار کردند. در سال ۱۹۹۸، ویلموس کومورنیک و پائولو لوریت، چنین مبناهای کوچکی را بررسی کردند (ثابت کومورنیک-لوریت q=۱٫۷۸۷۲۳۱۶۵۰...). در این مبنا، ۱=۰٫۱۱۰۱۰۰۱۱۰۰۱۰۱۱۰۱۰۰۱۰۱۱۰۰۱۱۰۱۰۰۱۱…؛ این ارقام از دنباله تئو-مورس به دست آمدهاند.[۲۷]
یک تعمیم دور از دسترستر، سیستمهای عددی موقعیتی استاندار را نشان میدهند. آنها نیز نمایشهای چند گانه دارند، و گاهی اوقات سختی آنها بیشتر ازست. برای مثال:[۲۸]
- در سیستم سهتایی متوازن، 1⁄2=۰٫۱۱۱…=۱٫۱۱۱… است.
- در سیستم معکوس اعداد فاکتوریل (استفاده از مبناهای ۲!، ۳!، ۴!، و ... برای مکان بعد از ممیز) ۱=۱٫۰۰۰…=۰٫۱۲۳۴… است.
عدم امکان نمایش واحد[ویرایش]
اینکه تمام این سیستمهای مختلف عددی از نمایش چندگانه برخی اعداد حقیقی رنج میبرند، را میتوان به تفاوت اساسی بین اعداد حقیقی به عنوان یک مجموعه مرتب و مجموعهای از رشتههای نامتناهی از نمادها نسبت داد. در حقیقت این دو ویژگی ذکر شده دلیل بر دشواری اند:
- اگر بازهای از اعداد حقیقی را به دو بخش غیر تهی L و R افزار کنیم، بهطوریکه تکتک اعضای L، کوچکتر از اعضای R باشند، یا L دارای بزرگترین عضو است، یا R دارای کوچکترین عضو میباشد، ولی هر دو اینها امکان ندارد.
- مجموعهای از رشته (علوم رایانه)/رشتههای نامتناهی از نمادهایی که در الفبای متناهی وجود دارند را میتوان به دو زیرمجموعه غیر تهی L و R تقسیم کرد، بهطوریکه هر عضو L کوچکتر از تکتک اعضای R، درحالی که L دارای بزرگترین عضو و R دارای کوچکترین عضو باشد. کافی است دو پیشوند p1 و p2 را از مجموعهای انتخاب کنید که تنها نماد آنها متفاوت باشد. هر نماد ارزشی متوالی دارد، و برای L مجموعهای از رشتهها را برگزینید پیشوند مربوطه آن حداکثر p1 باشد، و برای Rهای باقیمانده، رشتههایی از مجموعه را انتخاب کنید که پیشوند مربوطه حداقل p2 باشد. سپس L بزرگترین عنصر خواهد داشت، با p1 آغاز میشود و بزرگترین نماد را در تمام موقعیتهای بعدی انتخاب میکند، درحالی که R کوچکترین عنصر را دارد.
اولین نکته از ویژگیهای اساسی اعداد حقیقی ناشی میشود: L دارای کوچکترین کران بالا و R دارای بزرگترین کران پایین میباشد، که به راحتی میتوان دید برابرند. وجود یک عدد حقیقی که یا در R قرار دارد یا در L، ولی نه در هر دو، زیرا L و R مجموعههای مجزااند. نکته دوم جفت ۰٫۹۹۹…/۱٫۰۰۰… را برای p1 =”۰” و p2 تعمیم میدهد. در حقیقت نیاز نیست برای تمام موقعیتها از یک حرف استفاده کرد، (لذا برای مثال میتوان از ریشههای مختلط استفاده کرد) یا مجموعه کامل رشتههای ممکن را در نظر گرفت؛ تنها نکات مهم اینست که در هر موقعیت، میتوان از یک مجموعه متناهی از نمادها، انتخاب نمود، و اینکه داشتن انتخابی درست برای هر موقعیت میتواند موجب ایجاد یک رشته درست نامتناهی شود. با این فرضها، بحث بالا نشان میدهد که یک نقشه حفظ ترتیب، از مجموعه رشتهها تا یک بازه اعداد حقیقی، نمیتواند تابع دوسویی باشد: خواه برخی اعداد مطابق با رشته نباشند، یا برخی از آنها به بیش از یک رشته مربوط باشند.
مارکو پتکوسک، ثابت کردهاست، برای هر سیستم موقعیتی، که تمام اعداد حقیقی نام دارند، مجموعهای از اعداد حقیقی با نمایشهای چندگانه همواره ارزش دارند. او این اثبات را «یک تمرین آموزنده در توپولوژی نقطه-تنظیم ابتدایی» میخواند.[۲۹]
کاربردها[ویرایش]
یکی از کاربردهای ۰٫۹۹۹… به عنوان نمایشی از ۱، در سطح متوسط نظریه اعداد رایج است. در سال ۱۸۰۲، گودوین مشاهده ظهور ۹ها را در نمایشهای اعشار تکراری کسرهایی گزارش داد که مخرجهای آنان دارای اعداد اول معینی بودند. مثالها عبارتند از:
- 1⁄7= ۰٫۱۴۲۸۵۷۱۴۲۸۵۷… و ۱۴۲+۸۵۷=۹۹۹.
- 1⁄73= ۰٫۰۱۳۶۹۸۶۳۰۱۳۶۹۸۶… و ۰۱۳۶+۹۸۶۳=۹۹۹۹.
میدی یک نتیجه کلی از این کسرها گرفت که اکنون به قضیه میدی مشهور است. مطالب انتشار یافته از سوی او مبهم بودند و معلوم نبود اثباتهای او بهطور مستقیم شامل ۰٫۹۹۹… میشوند یا نه، ولی اثبات لیویت در آینده کار او را تکمیل کرد. اگر ثابت شود که یک عدد اعشاری به شکل 0.b1b2b3… یک عدد صحیح مثبت است، پس این عدد باید ۰٫۹۹۹… باشد که منبع ۹ها در این قضیه است.[۳۰] تحقیقات در این مسیر مفاهیمی مانند بزرگترین مقسومعلیه مشترک، همنهشتی، اعداد فرما، ترتیب در عناصر گروه (ریاضی)، و قانون تقابل درجه دوم را به حرکت واداشت.[۳۱]
با بازگشت به آنالیز حقیقی، در مبنای ۳، بهطور مشابه داریم ۰٫۲۲۲…=۱. این موضوع نقشی مهم در خصوصیات یکی از سادهترین اشکال خود متشابه ایفا میکند، وسط سوم مجموعه کانتور:
- نقطهای در بازه واحد، در مجموعه کانتور قرار دارد، تنها و تنها اگر بتوان آن را تنها با استفاده از ۰ و ۲ در مبنای ۳ نشان داد.
رقم nام این نمایش موقعیت نقطه در مرحله nام ساختار را نشان میدهد. برای مثال نقطه 2⁄3 دارای نمایش معمولی ۰٫۲ یا ۰٫۲۰۰۰…، در مبنای ۳ است، زیرا در سمت راست اولین حذف و سمت چپ هر حذف دیگر بعد از خودش قرار دارد.[۳۲]

۹های تکراری در یکی دیگر از کارهای جورج کانتور نیز به چشم میخورد. این موضوع به ساختار یک اثبات درست با استفاده از استدلال مورب او در سال ۱۸۹۱، برای توصیف بسط اعشاری، برای غیرقابل شمارش بودن بازه واحد، باز میگردد. چنین اثباتی نیاز به اعلام جفتهای معین از اعداد حقیقی میباشد که بسط اعشاری مختلفی دارند، لذا باید از جفتهایی مانند ۰٫۲ و ۰٫۱۹۹۹… احراض نمود. یک روش ساده نمایش همه با بسطی بیپایان بود؛ روشی مخالف تکرار 9.[۳۳] روش دیگری که مشابه بحث اصلی کانتر بود، استفاده از مبنای ۲ و تبدیل بسطهای مبنای ۳ به مبنای ۲ بود، که غیرقابل شمارش بودن مجموعه کانتر را اثبات میکرد.[۳۴]
تردید در آموزش[ویرایش]
دانشجویان ریاضی به دلایل مختلفی از ظاهر نامناسب تا شبهههای عمیق در مفهوم حد دنباله، همارزی ۰٫۹۹۹… و ۱ را رد میکنند و با طبیعت مقادیر بینهایت کوچک غیر صفر مخالفند. عوامل بسیاری هستند که به این سردرگمی کمک میکنند:
- دانشجویان اغلب به این مفهوم ذهنی تأکید دارند که یک عدد را تنها میتوان به یک شکل اعشاری نشان داد. مشاهده دو نمایش اعشاری کاملاً متفاوت برای یک عدد، یک پارادوکس به نظر میرسد، که با دیدن عدد آشکار ۱ تشدید میشود.[۳۵]
- برخی دانشجویان عدد ۰٫۹۹۹… را یک عدد بزرگ ولی دارای رشته محدود از ۹ها میپندارند، که دارای طولی قابل اندازهگیری ولی نامشخص است. اگر آنها یک رشته نامتناهی از ۹ را قبول کنند، در بینهایت، انتظار یک ۹ را خواهند داشت.[۳۶] تدریس نادرست سبب میشوند دانشجویان حد دنباله را به جای یک مقدار ثابت، نوعی از فرایند نامتناهی بپندارند، درحالی که یک دنباله هرگز به حد خود نمیرسد. زمانی که دانشجویان فرق بین دنباله اعداد و حد آن را قبول کنند، باید ۰٫۹۹۹… را با مفهوم دنباله مطالعه نمایند، نه حد.[۳۷]
این ایدهها در زمینه اعداد حقیقی استاندارد نادرستند، اگرچه ممکن استر برخی در سایر سیستمهای عددی درست باشند، سیستمهایی که یا برای کاربرد عمومی ریاضیات ایجاد شدهاند، یا به عنوان مثال نقض برای درک بهتر ۰٫۹۹۹… به کار میروند.
دیود تال بسیاری از این توضیحات را ابداع کردهاست، او ویژگیهای تدریس و درک را مطالعه نموده و از شبهههای پیش آمده در میان دانشجویانش بهره برده است. او با مصاحبه با دانشجویان دربارهٔ این که چرا خیل عظیم آنها این همارزی را رد میکنند، دریافتهاست، «دانشجویان اعتقاد دارند که ۰٫۹۹۹… دنبالهای از اعداد است که به ۱ نزدیک میشود، و یک مقدار ثابت نیست، زیرا از دیدگاه آنها، تعداد ۹ها نامعلوم است یا این عدد نزدیکترین عدد ممکن اعشاری به یک میباشد.»[۳۸]
با توجه به اثباتهای متوسط، ضرب ۰٫۳۳۳…=1⁄3 به ۳، یک استراتژی موفق در متعاقد نمودن دانشجویان مخالف است. زمانی که دانشجویان با تعارض بین اعتقاد به اولین معادله و عدم اعتقاد به دومین معادله روبهرو میشوند، برخی از آنها اعتقاد به اولین معادله کنار میگذارند و نا امید میشوند.[۳۹] روشهای اثبات پیچیدهتری وجود ندارد: دانشجویانی که کاملاً قادر به استفاده از توصیفات سخت میباشند، زمانی که با ریاضایت پیشرفته از جمله ۰٫۹۹۹… روبهرو میگردند، دچار تصورات حسی میشوند. برای مثال یک دانشجوی آنالیز حقیقی میتواند با استفاده از مفهوم سوپریمم، ثابت کند که ۰٫۳۳۳…=1⁄3 است، اما بر ۰٫۹۹۹…<1 که قبلاً در تقسیم طولانی دریافتهاست، تأکید میکند.[۴۰] دیگران هنوز میتوانند ثابت کنند که ۰٫۳۳۳…=۱، اما، با روبهرو شدن با اثبات کسری و تقسیم طولانی، پافشاری میکنند که «منطق» جایگزین محاسبات ریاضی شدهاست.
ژوزف مازور، داستان دانشجوی باهوش حساب خود را تعریف میکند، این دانشجو همه چیز را در کلاس درس به چالش میکشید جز محاسبات خود را، و به این اعتقاد رسیده بود که ارقام ۹، تمام چیزی هستند که ریاضیات باید انجام دهد، که شامل محاسبه جزر ۲۳ نیز میباشد. این دانشجو احساس خوبی نسبت به بحث حدی ۹٫۹۹۹…=۱۰ نداشت، و آن را «فرایند رشد بینهایت به شدت تصوری» خطاب میکرد.[۴۱]
اد دوبینسکی و همکارارنش، در سال ۲۰۰۵، به عنوان بخشی از تئوری آپوس، پیشنهاد میکنند که دانشجویانی که معتقدند مفهوم ۰٫۹۹۹… یک رشته متناهی نامعین است که فاصله آن با ۱ بینهایت کم میباشد، «هنوز یک فرایند درک کامل از اعداد اعشاری بینهایت به دست نیاوردهاند.» سایر دانشجویانی که فرایند مفهوم ۰٫۹۹۹… را کامل کردهاند، ممکن است قادر نباشند این فرایند را به یک «مفهوم هدف» محصور کنند (همانند مفهوم هدفی که از ۱ دارند)، و لذا آنها فرایند ۰٫۹۹۹… و ۱ را ناسازگار مییابند. دوبینسکی و همکاران، همچنین توانایی ذهنی محصور کردن را به درک 1⁄3 به عنوان یک عدد در جای خود و برای ارتباط با مجموعهای از اعداد طبیعی به عنوان یک کل واحد مربوط میکنند.[۴۲]
در فرهنگ عامه[ویرایش]
با توسعه اینترنت، بحث دربارهٔ ۰٫۹۹۹… از کلاسهای درس خارج شده و بهطور رایج در گروههای خبری و تالارهای گفتگومطرح گشته است، که بیشتر آنها ارتباط چندانی با ریاضیات ندارند. در گروه خبری sci.math بحث پیرامون ۰٫۹۹۹… با عنوان «ورزش محبوب» مطرح شدهاست، و یکی از سؤالاتی است که در پرسشگان بدان پاسخ دادهاند.[۴۳] پرسشگان بهطور خلاصه 1⁄3، ضرب در ۱۰، حدها و اشاره به دنباله کوشی را به خوبی پوشش داده است.
ویرایش ۲۰۰۳ مجله عمومی استرایت دوپ، با استفاده از 1⁄3 و مفهوم حد دنباله، پیرامون ۰٫۹۹۹… بحث میکند و تصورات نادرست را بیان میکند،
مهمل.[۴۴]
استرایت دوپ، در تالار گفتگوی خود بحثی را قرار داده است که از یک «تالار گفتگوی ناشناس دیگر... احتمالاً درباره بازیهای رایانهای» ایجاد شدهاست. در آنجا نیز سؤال ۰٫۹۹۹… محبوبیت این موضوع را در ۷ سال اول فروم battle.net بلیزارد انترتینمنت نشان میدهد که شرکت در روز دروغ اول آوریل سال ۲۰۰۴ بیان کرد که آن ۱ است:
ما خوشحال میشویم این بحث را یکبار و برای همیشه به پایان برسانیم. ما ناراحتی و نگرانیها را درباره اینکه آیا ۰٫۹۹۹… با ۱ برابر است یا نه، مشاهده نمودهایم و مفتخریم که این اثبات نهایتاً و بهطور قطع، مشکل مشتریانمان را حل کردهاست.[۴۵]
سپس ئو اثبات بر اساس مفهوم حد دنباله و ضرب در ۱۰ بیان شد.
ویژگیهای ۰٫۹۹۹… نیز به فرهنگ عامه ریاضایات تبدیل شدهاست، به خصوص در لطیفهها:[۴۶] سؤال: چند ریاضیدان لازم است تا یک لامپ برق را بچرخانند؟ پاسخ: ۰٫۹۹۹۹۹۹…
در سیستمهای عددی جایگزین[ویرایش]
اگرچه اعداد حقیقی یک سیستمعددی بسیار سودمند را ایجاد میکنند، تصمیم به درک مفهوم "۰٫۹۹۹…" به عنوان نامگذاری یک عدد حقیقی در نهایت یک قرارداد است، و تیم گورز، در کتاب خود به نام «ریاضیات: یک معرفی بسیار کوتاه» بیان میکند که نتیجه ۰٫۹۹۹…=۱ یک قرارداد است.
با این وجود این به معنای قراردادی دلخواه است، زیرا اتخاذ نکردن آن مجبور به اختراع موضوعات تازه عجیب میکند یا سبب رها کردن برخی قوانین آشکار حساب میگردد.[۴۶]
میتوان با استفاده از موضوعات جدید و قوانین مختلف، سیستمهای عددی تازهای را ایجاد کرد؛ در برخی از این سیستمها نیاز است که اثباتهای بالا دوباره تفسیر شوند و باید بدان نتیجه رسید که در یک سیستم عددی مفروض، ۰٫۹۹۹… و ۱ نباید برابر باشند. با اینحال بسیاری از سیستمهای عددی نوع گسترده (نه مستقل جایگزین) سیستم اعداد حقیقیاند، لذا ۰٫۹۹۹…=۱ آنجا نیز برقرار است. حتی در چنین سیسیتمهای عددی اگرچه، آزمایش سیستمهای عددی جایگزین ارزشمند است، و این موضوع نه تنها برای چگونگی رفتار ۰٫۹۹۹… صدق میکند (اگر) بلکه نحوه رفتار مفاهیم مرتبط را نیز در بر میگیرد.
مقادیر بینهایت کوچک[ویرایش]
برخی از اثباتهای ۰٫۹۹۹…=۱ به ویژگیهای حسابی اعداد حقیقی وابستهاند: در اعداد حقیقی مقادیر بسیار کوچک غیر صفر وجود ندارند. به ویژه مقدار ۱-۰٫۹۹۹…. کوچکتر از هر مقدار کسری است، لذا باید از مقادیر بینهایت کوچک باشد؛ از آنجا که اعداد حقیقی دارای مقادیر بسیار کوچک غیر صفر نمیباشند، لذا اختلاف آنها صفر است، و در نتیجه مقدار این دو عبارت برابر میباشد.
با این وجود، سیستمهای متصل ترتیبی بر پایه ساختار جبری، وجود دارند که شامل جایگزینهای مختلفی برای اعداد حقیقی میباشند و که غیر ارشمیدسی هستند. برای مثال، عدد دوگانه شامل یک علامت به معنای بینهایت کوچک میباشد (ε)، مشابه واحد فرضی i در سیستم عدد مختلط، ε۲ = ۰. از ای ن ساختار در مشتقگیری استفاده میشود. اعداد دوگانه میتوانند ترکیبی الفبایی فراهم کنند، که در آن مضاربی از ε عناصر غیر ارشمیدسی میباشند. بهیاد داشتهباشید این وجود، اعداد دوگانه نیز عبارت ۰٫۹۹۹…=۱ را تصدیق میکنند. باید توجه کرد که از آنجا که در سیستم اعداد دوگانه، ε وجود دارد، لذا ε/۲ نیز وجود دارد، پس ε کوچکترین مقدار مثبت عدد دوگانه نیست، و البته در اعداد حقیقی چنینی عددی وجود ندارد.
آنالیزهای غیر استاندارد یک سیستم عددی با آرایهای از مقادیر بسیار کوچک را فراهم میکنند.[۴۷] ای. لایتستون بسط اعشاری اعداد فراحقیقی در (۰, ۱) توسعه داده است.[۴۸] او نشانداده است که چگونه میتوان به هر عدد یک دنباله از ارقام را نسبت داد،
که با نمایه اعداد فراصحیح نمایش یافتهاند. اگرچه او بهطور مستقیم ۰٫۹۹۹… را مورد بحث قرار نداده است، ولی نشان داده که عدد حقیقی ۱/۳ را میتوان به شکل ۰٫۳۳۳…؛…۳۳۳… نمایش داد، که نتیجه اصل انتقال است. در نتیجه ۰٫۹۹۹…. ؛…۹۹۹…=۱ است. با این نمایش اعشاری، تمام بسطها یک عدد را نشان نمیدهند. در حقیقت، اعداد ۰٫۳۳۳…؛…۰۰۰… و ۰٫۹۹۹…؛…۰۰۰…، به هیچ عددی مربوط نمیشوند.
تعریف استاندارد ۰٫۹۹۹…، حد دنباله ۰٫۹،۰٫۹۹، ۰٫۹۹۹ و … میباشد. یک تعریف دیگر، یک کلاس همارزی از دنبالهها را در ساختار فرانیرو فراهم میکند، که مربوط به عددی است که به اندازه بینهایت کوچک، از عدد ۱ کمتر است. بهطور عمومیتر، عدد فراحقیقی uH=۰٫۹۹۹... ;...۹۹۹۰۰۰... با اتمام ۹ها در بینهایت، رشتهای را ایجاد میکند که کوچکتر از ۱ است. بر این اساس، کارین کاتز و میکائیل کاتز، یک تفسیر جایگزین از "۰٫۹۹۹…" را مطرح کردهاند:
تمام این تفاسیر در بینهایت نزدیک به ۱ هستند. ایان استوارت این تفاسیر را به عنوان یک راه کاملاً عاقلانه باری توجیه دقیق این موضوع به کار میبرد، که ۰٫۹۹۹… اندکی با ۱ اختلاف دارد.[۴۹] روبرت الی، به همراه کاتزها، این فرض را مورد سؤال قرار میدهد که ایده دانشجویان دربارهٔ ۰٫۹۹۹…<1، یک تصور اشتباه دربارهٔ اعداد حقیقی است، او تفسیر آنان را یک درک غیر استاندارد معرفی میکند ک هدر آموزش حساب ارزشمندند. جوز به ندرت در کتاب خود به نام بینهایت: مقالهای پیرامون متافیزیک، بیان میکند که درکهای طبیعی پیشریاضی قابل بیان نخواهند بود، اگر یکی از آنها به یک سیستم عددی بسیار محدود، بسته شود:
قابلیت فهم این زنجیره بارها نشان داده است که نیاز به بزرگی دامنه اعداد حقیقی وجود دارد که شامل مقادیر بسیار کوچک میشود. این دامنه بزرگشده، دامنه اعداد زنجیرهای را شکل داد. اکنون بدیهی است که ۰٫۹۹۹۹… برابر ۱ نیست، بلکه به اندازه بینهایت کوچک، از آن کمتر است. به نظر من باید ۰٫۹۹۹۹… را یک عدد مجزا در نظر گرفت... اگرچه نه یک عدد حقیقی.[۵۰]
هاکنبوش[ویرایش]
نظریه بازی ترکیبی اعداد حقیقی را فراهم میکند، که بازی آبی قرمز هاکنبوش یک مثال مرتبط است. در سال ۱۹۷۴، الوین برلکمپ ارتباطی بین رشتههای هاکینپوش و بسط دوتایی اعداد حقیقی توصیف میکند، که از ایده فشردهسازی دادهها شکل گرفتهاست. برای مثال، مقدار رشته هاکنبوش LRRLRLRL… برابر 0.0101012…=1⁄3 میباشد. اما مقدار LRLLL… به اندازه بینهایت کوچک، از ۱ کمتر است. تفاوت ایندو عدد سورئال میباشد، 1⁄ ω که ω اولین عدد ترتیبی بینهایت است؛ بازی مربوط LRRRR… یا 0.000...2 میباشد.[۵۱]
بازنگری تفریق[ویرایش]
یکی دیگر از روشهایی که اثباتها را زیر سؤال میبرد، این است که آیا ۱-۰٫۹۹۹… وجود دارد، زیرا همیشه تفریق امکانپذیر نیست. ساختارهای ریاضی با عملگرد جمع، نه تفریق، شامل خاصیت جابجایی و جابجایی مونوئیدها میباشد. ریچمن دو سیستم اینچنینی را در نظر میگیرد، لذا ۰٫۹۹۹…<1 است.
او ابتدا یک عدد اعشاری غیر منفی را به عنوان بسط اعشاری در نظر میگیرد. او بیان میکند که ۰٫۹۹۹…<1 است زیرا ۰<1 میباشد، ولی برای هر x بدون واحد، داریم x+1=x+0.999.... لذا یکی از خاصیتهای اعداد اعشاری اینست که جمع همواره متوقف نمیشود؛ خاصیت بعدی اینست که عدد اعشاری با 1⁄3 مرتبط است. بعد از تعریف ضرب، اعداد اعشاری یک نیمحلقه جابجاییپذیر، کاملاً مرتب و مثبت را شکل میدهد.[۵۲]
ریچمن در فرایند معرفی ضرب، یک سیستم دیگر به نام «برش دی» را معرفی میکند که مجموعهای از برشهای ددکیند برای کسرهای اعشاری است. معمولاً این تعریف به یک عدد حقیقی میانجامد، اما برای یک کسر اعشاری d، او اجازه ایجاد برشهای (−∞, d) و (−∞, d] فراهم میکند. نتیجه اینست که اعداد حقیقی با کسرهای اعشاری به سختی با یکدیگر کنار میآیند. دوباره ۰٫۹۹۹…<1 است. در برش D هیچ مقدار بسیار کوچک مثبتی وجود ندارد، اما نوعی مقدار بینهایت کوچک منفی موجود است، 0−، که هیچ بسط حقیقی ندارد. او میگوید ۰٫۹۹۹…=1+0−، درحالی که معادله "۰٫۹۹۹…+1=x پاسخی ندارد.[۵۳]
سؤالات مربوط[ویرایش]
- پارادوکسهای زنون، بهویژه پارادوکس دونده، یادآور پارادوکس موجود در برابری ۰٫۹۹۹… و ۱ میباشد. پارادوکس دونده را میتوان همانند ۰٫۹۹۹…، مدلسازی ریاضی کرد، و با سریهای هندسی حل نمود. با این وجود، معلوم نیست که آیا این رفتار ریاضی، موضوع متافیزیکی زنون را بهطور کامل بررسی میکند.[۵۴]
- بخش بر صفر در برخی بحثهای مشهور ۰٫۹۹۹… روی میدهد و موجب مشاجرات فراوانی شدهاست. اگرچه بسیاری از ریاضیدانان ۰٫۹۹۹… را تعریف شده میدانند، بسیاری از روشهای مدرن تقسیم بر صفر را تعریفنشده میخوانند، زیرا هیچ مفهومی در اعداد حقیقی استاندارد ندارد. اما تقسیم بر صفر در برخی سیستمهای دیگر مانند آنالیز مختلط، تعریف شده است، جاییکه صفحه مختلط گسترشیافته، به عنوان مثال کره ریمان، در بینهایت، نقطهای دارد. اینجا، تعریف 1⁄0 به عنوان مفهوم بینهایت معنی دارد؛[۵۵] و در حقیقت نتایج برای بسیاری از مسائل مهندسی و فیزیک عمیق و مناسبند. برخی ریاضیدانان برجسته، خیلی قبلتر از توسعه سیستم اعداد در این باره بحث کردهاند.[۵۶]
- صفر منفی یکیدیگر از ویژگیهای اضافی روشهای مختلف نوشتن است. در سیستمهای عددی، مانند اعداد حقیقی، که "۰"، هویتی افزودنی را نشان میدهد و نه منفی و نه مثبت میباشد، تفسیر معمول "-۰" باید به این معنا باشد که این عدد مخالف صفر است، که موجب میشود، −۰ = ۰ باشد.[۵۷] با این وجود، برخی کاربردهای علمی، از صفرهای مثبت و منفی بهطور جداگانه استفاده میکنند، مانند برخی سیستمهای محاسبه دوتایی.[۵۸][۵۹]
جستارهای وابسته[ویرایش]
پیوند به بیرون[ویرایش]
- .۹۹۹۹۹۹… = ۱?
- چرا ۰٫۹۹۹ با یک برابر است؟
- Ask A Scientist: Repeating Decimals
- Proof of the equality based on arithmetic
- Repeating Nines
- Point nine recurring equals one
- David Tall's research on mathematics cognition
- Theorem ۰٫۹۹۹... در متامت
منابع[ویرایش]
- ↑ This argument is found in Peressini and Peressini p. 186. William Byers argues that a student who agrees that 0.999... = 1 because of the above proofs, but hasn't resolved the ambiguity, doesn't really understand the equation (Byers pp. 39–41). Fred Richman argues that the first argument "gets its force from the fact that most people have been indoctrinated to accept the first equation without thinking".(p. 396)
- ↑ Rudin p. 61, Theorem 3.26; J. Stewart p. 706
- ↑ Euler p. 170
- ↑ Grattan-Guinness p. 69; Bonnycastle p. 177
- ↑ For example, J. Stewart p. 706, Rudin p. 61, Protter and Morrey p. 213, Pugh p. 180, J.B. Conway p. 31
- ↑ The limit follows, for example, from Rudin p. 57, Theorem 3.20e. For a more direct approach, see also Finney, Weir, Giordano (2001) Thomas' Calculus: Early Transcendentals 10ed, Addison-Wesley, New York. Section 8.1, example 2(a), example 6(b).
- ↑ Davies p. 175; Smith and Harrington p. 115
- ↑ Beals p. 22; I. Stewart p. 34
- ↑ Bartle and Sherbert pp. 60–62; Pedrick p. 29; Sohrab p. 46
- ↑ Apostol pp. 9, 11–12; Beals p. 22; Rosenlicht p. 27
- ↑ Apostol p. 12
- ↑ The historical synthesis is claimed by Griffiths and Hilton (p.xiv) in 1970 and again by Pugh (p. 10) in 2001; both actually prefer Dedekind cuts to axioms. For the use of cuts in textbooks, see Pugh p. 17 or Rudin p. 17. For viewpoints on logic, Pugh p. 10, Rudin p.ix, or Munkres p. 30
- ↑ Enderton (p. 113) qualifies this description: "The idea behind Dedekind cuts is that a real number x can be named by giving an infinite set of rationals, namely all the rationals less than x. We will in effect define x to be the set of rationals smaller than x. To avoid circularity in the definition, we must be able to characterize the sets of rationals obtainable in this way..."
- ↑ Rudin pp. 17–20, Richman p. 399, or Enderton p. 119. To be precise, Rudin, Richman, and Enderton call this cut 1]], 1−, and 1R, respectively; all three identify it with the traditional real number 1. Note that what Rudin and Enderton call a Dedekind cut, Richman calls a "nonprincipal Dedekind cut".
- ↑ Richman p. 399
- ↑ ۱۶٫۰ ۱۶٫۱ O'Connor, J. J.; Robertson, E. F. (October 2005). "History topic: The real numbers: Stevin to Hilbert". MacTutor History of Mathematics. Archived from the original on 29 September 2007. Retrieved 2006-08-30.
- ↑ "Is 0.999... = 1?". Archived from the original on 11 December 2014. Retrieved 6 November 2014.
- ↑ Richman
- ↑ Richman pp. 398–399
- ↑ Griffiths & Hilton §24.2 "Sequences" p. 386
- ↑ Griffiths & Hilton pp. 388, 393
- ↑ Griffiths & Hilton p. 395
- ↑ Griffiths & Hilton pp.viii, 395
- ↑ Liangpan Li (March 2011). "A new approach to the real numbers". arXiv:1101.1800 [math.CA].
{{cite arxiv}}: Unknown parameter|deadurl=ignored (help) - ↑ Petkovšek p. 408
- ↑ Protter and Morrey p. 503; Bartle and Sherbert p. 61
- ↑ Komornik and Loreti p. 636
- ↑ Kempner p. 611; Petkovšek p. 409
- ↑ Petkovšek pp. 410–411
- ↑ Leavitt 1984 p. 301
- ↑ Lewittes pp. 1–3; Leavitt 1967 pp. 669, 673; Shrader-Frechette pp. 96–98
- ↑ Pugh p. 97; Alligood, Sauer, and Yorke pp. 150–152. Protter and Morrey (p. 507) and Pedrick (p. 29) assign this description as an exercise.
- ↑ Maor (p. 60) and Mankiewicz (p. 151) review the former method; Mankiewicz attributes it to Cantor, but the primary source is unclear. Munkres (p. 50) mentions the latter method.
- ↑ Rudin p. 50, Pugh p. 98
- ↑ Bunch p. 119; Tall and Schwarzenberger p. 6. The last suggestion is due to Burrell (p. 28): "Perhaps the most reassuring of all numbers is 1 ... So it is particularly unsettling when someone tries to pass off 0.9~ as 1."
- ↑ Tall and Schwarzenberger pp. 6–7; Tall 2000 p. 221
- ↑ Tall and Schwarzenberger p. 6; Tall 2000 p. 221
- ↑ Tall 2000 p. 221
- ↑ Tall 1976 pp. 10–14
- ↑ Pinto and Tall p. 5, Edwards and Ward pp. 416–417
- ↑ Mazur pp. 137–141
- ↑ Dubinsky et al. pp. 261–262
- ↑ As observed by Richman (p. 396). de Vreught, Hans (1994). "sci.math FAQ: Why is 0.9999... = 1?". Archived from the original on 29 September 2007. Retrieved 2006-06-29.
- ↑ Adams, Cecil (2003-07-11). "An infinite question: Why doesn't .999~ = 1?". The Straight Dope. Chicago Reader. Archived from the original on 15 August 2006. Retrieved 2006-09-06.
- ↑ Renteln and Dundes, p. 27
- ↑ ۴۶٫۰ ۴۶٫۱ Gowers p. 60
- ↑ For a full treatment of non-standard numbers see for example Robinson's Non-standard Analysis.
- ↑ Lightstone pp. 245–247
- ↑ Stewart 2009, p. 175; the full discussion of 0.999... is spread through pp. 172–175.
- ↑ Benardete, José Amado (1964). Infinity: An essay in metaphysics. Clarendon Press. p. 279. Retrieved 27 November 2011.
- ↑ Berlekamp, Conway, and Guy (pp. 79–80, 307–311) discuss 1 and 1/3 and touch on 1/ω. The game for 0.111...2 follows directly from Berlekamp's Rule.
- ↑ Richman pp. 397–399
- ↑ Richman pp. 398–400. Rudin (p. 23) assigns this alternative construction (but over the rationals) as the last exercise of Chapter 1.
- ↑ Wallace p. 51, Maor p. 17
- ↑ See, for example, J.B. Conway's treatment of Möbius transformations, pp. 47–57
- ↑ Maor p. 54
- ↑ Munkres p. 34, Exercise 1(c)
- ↑ Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2e ed.). W. H. Freeman. p. 462. ISBN 0-7167-1088-9.
- ↑ "Floating point types". MSDN C# Language Specification. Archived from the original on 24 August 2006. Retrieved 2006-08-29.
- ترجمه از ویکیپدیا انگلیسی



















