الگوریتم تصادفی
لحن یا سبک این مقاله بازتابدهندهٔ لحن دانشنامهای مورد استفاده در ویکیپدیا نیست. |

در این مقاله شما با الگوریتمهای تصادفی و انواع آن و تاریخچه الگوریتمهای تصادفی آشنا میشوید و همچنین به بررسی و تحلیل الگوریتمهای تصادفی می پردازیم . در ضمن در انتها چند مثال از الگوریتمهای تصادفی را بررسی میکنیم.
چکیده[ویرایش]
بهطور خلاصه، تحلیل احتمالی، استفاده از احتمال در تحلیل مسئله میباشد این موضوع معمولاً موقعی به کار میرود که بدترین حالت اجرای یک الگوریتم دارای احتمال ناچیزی باشد و می خواهیم کارایی برنامه را در حالت متوسط بدست بیاوریم و این موضوع را میتوان با تحلیل احتمالی به راحتی بدست آورد.
الگوریتم تصادفی به الگوریتمی گفته میشود که رفتارش نه تنها به اندازهٔ ورودی بلکه همچنین با مقادیر تولید شده توسط یک مولد تصادفی تعیین میشود. بنابراین در این نوع الگوریتم فرض میکنیم ماشینی که در آن الگوریتم خود را پیادهسازی میکنیم باید قابلیت تولیدکننده یاعداد تصادفی را داشته باشد.
الگوریتم تصادفی[ویرایش]
الگوریتمی است که در آن ماشین به تولید اعداد تصادفی دسترسی دارد و از آن در الگوریتم خود استفاده میکند. این الگوریتم نوعاً با هدف بالا بردن کارایی در حالتهای معمول از یک ورودی دودویی کمکی برای رفتارهای خود استفاده میکند. کارایی الگوریتم با یک متغیر تصادفی که به بیتهای تصادفی داده شدهاست بستگی دارد و تغییر مییابد که باعث مشود امید ریاضی خوبی را شامل شود. احتمال وقوع بدترین حالت بسیار کم است و میتوان از آن صرفنظر کرد.

میزان واقعیت الگوریتم های تصادفی[ویرایش]
همان طور که در شکل سمت چپ مشخص است با افزایش محور افقی و با احتمال نزدیک به ۱۰۰ درصد نتیجهٔ حاصل نزدیک به واقعیت میباشد. (برای اطلاعات بیشتر از نحوهٔ بدست آوردن این صفحه میتوانید به لینک آن مراجعه نمایید.)
مرتبسازی سریع یکی از مهمترین الگوریتمهای تصادفی میباشد که وقوع بدترین حالت خیلی کم است و با تحلیل احتمالی این موضوع را نشان میدهیم و همچنین نوع Randomize Quick Sort که یک الگوریتم تصادفی است فقط به ورودی آرایهای مربوط نمیباشد بلکه به یک عدد تصادفی تولید شده نیز مربوط است.
به عنوان مثال فرض کنید در آرایهای که شامل اعداد صفر و یک میباشد بهطوری که نصف آنها صفر و نیمی دیگر یک هستند می خواهیم با عمل جستجو کردن از ابتدای آرایه اولین عنصر با مقدار بک را بیابیم. این مسئله در بدترین حالت باید (N/2) نیمی از خانه های آرایه را بررسی کنیم تا اولین یک را پیدا کنیم احتمال وقوع چنین حالتی بسیار کم است. از طرفی در حالت متوسط تعداد عمل جستجو برای این آرایه و پیدا کردن اولین یک کمتر از پیدا کردن اولین یک در حالت بدترین است.
موارد استفاده الگوریتمهای تصادفی[ویرایش]
۱. الگوریتمهای تصادفی به ویژه در مواردی استفاده دارند که با یک دشمن یا مهاجم بد خواهی! مواجهیم که از روی عناد ورودی بدی را برای ما فراهم میکند(آنالیز رقابتی). به همین دلیل انتخاب تصادفی پایه رمزنگاری را تشکیل میدهد. این بدین معنی است که دشمن شما(!) نمیتواند با یک ورودی خاص بدترین حالت (Worst Case)شما را پدید بیاورد چون که به اعداد تصادفی تولید شده نیز مربوط میباشد.
۲. از الگوریتمهای تصادفی معمولاً برای بررسی پدیدههایی مورد استفاده قرار میگیرند که در آنها تعداد زیاد باشد. برای مثال واپاشی هستهای یک هسته پرتوزا را در نظر میگیریم. برای بررسی این پدیده که چه زمانی یک اتم از آن واپاشی میکند ناچار به استفاده از احتمال هستیم. یعنی بهتر است بگوییم احتمال واپاشی این اتم چه قدر است. حالا اگر تعداد اتمها زیاد باشد، دیگر مسئله را از طریق تحلیلی نمیتوان حل کرد. بلکه باید به روشهای عددی روی آورد. در حقیقت الگوریتمهای تصادفی، راهی برای حل عددی اینگونه مسائل هستند.
انواع الگوریتمهای تصادفی[ویرایش]
در مثال بالا الگوریتم تصادفی همیشه درست جواب میدهد تنها احتمال کوچکی وجود دارد که زمان زیادی برای رسیدن به پاسخ صرف کند. در بعضی مواقع ما از الگوریتم با اجازه دادن ایجاد احتمال کمی خطا انتظار سرعت بالاتر را داریم. الگوریتمهای از نوع اول را لاس وگاس (Las Vegas algorithms) و نوع اخیر را مونت کارلو (Monte Carlo algorithms) مینامند. مشاهده میکنیم که هر الگوریتم لاس وگاس با گرفتن جوابی احتمالاً نادرست در زمانی مشخص و محدود شده به الگوریتم مونت کارلو تبدیل میشود.
از الگوریتمهای تصادفی معمولاً برای بررسی پدیدههایی مورد استفاده قرار میگیرند که در آنها تعداد زیاد باشد. برای مثال واپاشی هستهای یک هسته پرتوزا را در نظر میگیریم. برای بررسی این پدیده که چه زمانی یک اتم از آن واپاشی میکند ناچار به استفاده از احتمال هستیم. یعنی بهتر است بگوییم احتمال واپاشی این اتم چه قدر است. حالا اگر تعداد اتمها زیاد باشد، دیگر مسئله را از طریق تحلیلی نمیتوان حل کرد. بلکه باید به روشهای عددی روی آورد. در حقیقت الگوریتمهای تصادفی، راهی برای حل عددی اینگونه مسائل هستند.
در آزمایشگاه لوس آلاموس در آمریکا دانشمندانی که بر روی پروژه سری منهتن کار میکردند، برای بررسی سیستمهایی که درآنها تعداد ذرات بالااست، مجبور به ابداع روش یا الگوریتمی شدند که بعدها نام «مونت کارلو» بر آن قرار دادند. این الگوریتم برای نمونهگیری آماری از سیستمهایی با تعداد فضای فاز بالا به کار میرود. همچنین از این الگوریتم برای حل معادلات دیفرانسیل و انتگرالگیری معین استفاده میشود. دو الگوریتم مشهور مونت کارلو عبارتند از:
- الگوریتم متروپلیس
- الگوریتم مونت کارلو جنبشی یا n-fold way.
این الگوریتمها بیشتر بر این مبنا کار میکنند که:ابتدا یک پیکر بندی از سیستم مورد بررسی انتخاب میشود. سپس راههای موجود برای اینکه سیستم به آنها گذار کند مشخص احتمال آنها محاسبه میشود. آنگاه با تولید یک عدد تصادفی احتمالات موجود مورد سنجش قرار میگیرند، و سیستم به یکی از حالات ممکن گذار میکند. دوباره قسمت دیگری از سیستم انتخاب شده و مراحل قبلی تکرار میشود.
مثال: مسئله استخدام[ویرایش]
فرض کنید شما به استخدام یک منشی در شرکت خود نیاز دارید و چون تلاشهای گذشتهی شما بی نتیجه مانده است از یک آژانس کاریابی کمک میگیرید. این آژانس هر روز برای شما یک داوطلب استخدام میفرستد. شما با فرد متقاضی مصاحبه کرده و تصمیم میگیرید که او را استخدام کنید یا نه. شما هر بار برای مصاحبه با یک نفر باید مبلغ کمی به آژانس پرداخت کنید. شما میخواهید هر بار بهترین فرد ممکن را به عنوان منشی استخدام کنید و این کار با اخراج منشی قبلی و استخدام فرد جدید و پرداخت پول هم راه است. برای آن که همیشه بهترین فرد منشی استخدامی شما باشد بعد از مصاحبه با هر نفر اگر او از فرد قبلی بهتر بود او را استخدام میکنید. شما میخواهید هزینه این کار را قبل از شروع استخدام تخمین بزنید. در زیر یک الگوریتم ساده که گویای این عملیات است ارائه شدهاست:
مصاحبه کردن برای استخدام قیمت کمی را در بر دارد که آن را با ci عنوان میکنیم ولی آگهی استخدام قیمت بالایی در بر دارد که با ch نشان میدهیم. اگر از بین n نفر m تایشان استخدام شوند هزینهٔ کل از O(nci + Onch) l است.
در بدترین حالت ما باید همهٔ داوطلبان را استخدام کنیم که هزینه از O(nch)l میشود.
برای آن که بتوانیم متوسط هزینه استخدام را تخمین بزنیم فرض میکنیم داوطلبان به صورت رندوم میآیند. این به این معناست که ما گویی قبل از ورود داوطلبان جایگاه هر کدام از نظر خوب تر بودن را به ترتیب میدانیم و هرروز به صورت رندوم از میان این n نفر یکی را انتخاب میکنیم.(می دانیم که این انتخاب ما به صورت رندوم یک انتخاب خوب است) برای محاسبهٔ هزینه میانگین با این توضیحات از ایدهٔ متغیر تصادفی استفاده میکنیم.
تحلیل[ویرایش]
X را یک متغیر تصادفی میگیریم که برابر است با تعداد دفعاتی که ما یک منشی استخدام میکنیم. میدانیم:
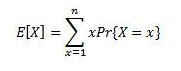
ولی محاسبهٔ این سیگما هنوز مشکل است. پس X را به n متغیر تصادفی دیگر تقسیم میکنیم.

و میدانیم:

طبق قوانین ریاضی مینویسیم:

منابع[ویرایش]
- Knuth, Donald. The Art of Computer Programming (Volume 1 / Fundamental Algorithms), 2nd Printing. USA: Addison-Wesley Publishing, 1969.
- Cormen, Thomas H. (et al), Intorduction to Algorithms (2nd Edition), USA: McGraw-Hill, 2001. ISBN 0-07-013151-1
- هورویتز، الیس. طراحی الگوریتمها، چاپ دوم (مترجم: علیخانزاده، امیر). مشهد: پرتونگار، ۱۳۸۵.
- کرمن/لیرسون /ریورست/استین، کتاب طراحی مقدمهای بر طراحی الگوریتمها، چاپ چهارم(مترجم : گروه مهندسی پژوهشی خوارزمی) فصل ششم، مشهد(1387)
جستارهای وابسته[ویرایش]
| در ویکیانبار پروندههایی دربارهٔ الگوریتم تصادفی موجود است. |