تداخلسنج فابری-پرو
در نورشناسی، تداخل سنج فابری- پرو یا اتالون، از یک تیغه شفاف با دو سطح بازتابنده یا از دو آینه موازی با بازتابندگی زیاد ساخته میشود. (از نظر فنی باید تیغه اول را اتالون و دو آینه را تداخل سنج نامید، ولی معمولاً این دو اصطلاح را به جای هم به کار میبرند.) طیف عبوری تابعی از طول موج است که پیکهایی بزرگ از تشدیدهای عبوری اتالون نشان میدهد. نام این تداخل سنج از نامهای چارلز فابری و آلفرد پرو گرفته شدهاست. واژه اتالون از واژه فرانسوی étalon به معنی پیمانه اندازهگیری یا استاندارد گرفته شدهاست.
اثر تشدیدی تداخل سنج فابری-پرو مشابه فیلترهای دورنگی است. پس فیلترهای دورنگی چیدمان مرتبی از تداخل سنجهای فابری- پرو هستند که توسط ریاضیات مشابهی توصیف و طراحی میشود. اتالونها به صورت بسیار وسیع در ارتباطات راه دور، لیزرها و طیف سنجی برای کنترل و اندازهگیری طول موجهای نور استفاده میشود.
توصیف بنیادی[ویرایش]
قلب تداخل سنج فابری- پرو یک جفت شیشه نیمه بازتابنده تخت است که به فاصله چند میلی متر یا سانتی متر از هم قرار دارند، که سطوح بازتابنده مقابل هم قرار دارند. ( ... ، یک اتالون فابری- پرو از تیغه با دوسطح بازتابنده موازی استفاده میکند.) صفحات تخت در یک تداخل سنج اکثراً به شکل گوهای ساخته میشوند تا از تولید فرانژهای تداخلی ناشی از صفحات پشتی جلوگیری کند؛ صفحات پشتی همچنین پوشش ضد بازتاب دارند. در یک سیستم عادی، نوردهی به وسیلهٔ یک چشمه پهن انجام میشود که در صفحه کانونی یک لنز همگراکننده قرار دارد. اگر صفحات وجود نداشتند یک لنز کانونیکننده بعد از جفت صفحات تخت باعث تشکیل یک تصویر وارونه از چشمه می شد؛ تمام پرتوهای ساطع شده از چشمه در یک نقطه در صفحه تصویر سیستم کانونی می شد. در تصویر نشان داده شده، تنها پرتو ای که از نقطه A ساطع شده ردگیری شدهاست. همچنان که پرتواز جفت صفحات تخت میگذرد، چندین بار بازتاب میشود و چند پرتوی عبوری دیگر تولید میکند که بهوسیلهٔ لنز کانونیکننده در صفحه نمایش در نقطه Á جمعآوری میشود. طرح تداخلی تکمیل شده به شکل حلقههای هم مرکز در میآید. تیزی حلقهها به بازتاب آینهها بستگی دارد. اگر بازتاب زیاد باشد، در نتیجه زیاد بودن ضریب Q ، نور تک رنگ یک مجموعه از حلقههای باریک و نورانی در پس زمینهای تاریک درست میکند. یک تداخل سنج فابری- پرو با ضریب بالای Q را دارای ظرافت بالا می نامند.
کاربردها[ویرایش]
بیشترین کاربرد رایج این تداخل سنج استفاده در فیلترهای دورنگی میباشد، که در آن تعدادی از اتالونها روی یک سطح اپتیکی بهوسیلهٔ لایه نشانی تبخیری نشانده میشوند. این فیلترهای اپتیکی معمولاً پهنای بازتاب و عبور دقیق تری نسبت به فیلترهای جذبی دارند. وقتی این فیلترها دقیق طراحی شده باشند، چون طول موجهای اضافی را جذب نمیکنند همواره خنک ترند. در شبکههای ارتباط راه دور از تقسیمکنندههای طول موج یا ترکیبکنندههای اتالون از جنس سیلیکون ناخالص یا الماس استفاده میشود. الماس مادهای مناسب برای ساختن اتالون است زیرا رسانش گرمایی بالا دارد ولی همچنان ضریب پخش پایین خود را حفظ میکند. در سال 2005 تعدادی از شرکتهای تجهیزات ارتباط راه دور شروع به استفاده از اتالونهای جامد که خود فیبر نوری نیز هستند کردند. تشدیدکنندههای لیزری معمولاً به عنوان تشدیدکنندههای فابری- پرو معرفی میشوند. لیزرهای نیمه رسانا گاهی از هندسهٔ فابری- پرو استفاده میکنند، بخاطر سختی در لایه نشانی سطوح کوچک ته مدارها.
تئوری[ویرایش]
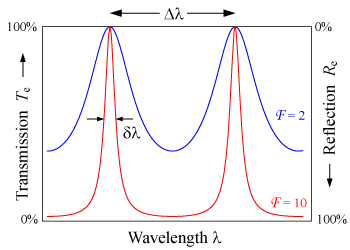
تفاوت در تابع عبور یک اتالون بخاطر تداخل بین بازتابهای زیاد بین دو سطح میباشد. تداخل سازنده بخاطر همفاز بودن پرتوهای عبوری اتفاق می افتد، و باعث یک عبور با شدت بالا در اتالون میشود. اگر پرتوهای عبوری همفاز نباشند، تداخل ویرانگر اتفاق افتاده باعث عبور حداقلی میشود. پرتوهای بازتابی چه همفاز باشند چه نه بستگی به طول موج نور، زاویهای که نور در اتالون حرکت میکند، ضخامت اتالون و ضریب شکست مادهٔ بین سطوح بازتابی دارد. اختلاف فاز بین دو بازتاب موفق برابر است با δ
اگر هر دو سطح دارای ضریب بازتاب R باشند، تابع عبور اتالون برابر است با
جایی که
ضریب ظرافت است. حداکثر عبور () زمانی اتفاق می افتد که اختلاف راه نوری () بین هر دو پرتوی عبوری ضریب صحیحی از طول موج باشد. بدون حضور جذب، بازتابندگی اتالون مکمل عبور است، مثل .حداکثر بازتاب برابر است با
و این هنگامی اتفاق می افتد که اختلاف راه نیم مضرب فردی از طول موج باشد. ضریب ظرافت نیز (برای R > 0.5) از رابطهٔ زیر تخمین زده میشود:









