نوسان‌ساز آرامشی

چشمک زن چراغ راهنما در وسایل نقلیه موتوری با یک نوسان‌ساز آرامشی ساده که یک رله را تأمین انرژی می‌کند، تولید می‌شود.

در الکترونیک یک نوسان‌ساز آرامشی یک مدار نوسان‌ساز الکترونیکی غیر خطی است که یک سیگنال خروجی تکراری غیرسینوسی، مانند یک موج مثلثی یا موج مربعی را تولید می‌کند. این مدار شامل یک حلقه بازخورد است که حاوی یک قطعه کلیدزنی مانند ترانزیستور، مقایسه‌کننده، رله، آمپ‌امپ یا یک قطعه با مقاومت منفی مانند دیود تونلی است که به‌طور مکرر خازن یا سلفی را از طریق یک مقاومت شارژ می‌کند تا زمانی که به یک سطح آستانه برسد، سپس دوباره آن را تخلیه می‌کند. دوره تناوب نوسان‌ساز به ثابت زمانی مدار خازنی یا سلفی بستگی دارد. قطعات فعال به‌طور ناگهانی بین حالت شارژ و تخلیه سوئیچ می‌کند و بنابراین شکل‌موج تکراری متناوب متغییری تولید می‌کند. این در تضاد با دیگر انواع نوسان‌ساز الکترونیکی، نوسان‌ساز هارمونیکی یا خطی است که از یک تقویت‌کننده با بازخورد برای تحریک نوسانات تشدیدی در یک تشدیدگر و تولید یک موج سینوسی استفاده می‌کند. نوسان‌سازهای آرامشی برای تولید سیگنال‌هایی با فرکانس پایین برای کاربردهایی مانند چراغ چشمک زن (چراق راهنما) و بوق‌های الکترونیکی و در نوسان‌سازهای کنترل‌شده با ولتاژ (وی‌سی‌او)، اینورترها و منبع تغذیه کلیدزنی، مبدل‌های آنالوگ به دیجیتال دو-شیب و فانکشن ژنراتور استفاده می‌شوند.

اصطلاح نوسان‌ساز آرامشی همچنین در بسیاری از زمینه‌های گوناگون علوم که نوسانات غیرخطی تولید می‌کنند به سیستم‌های دینامیکی اطلاق می‌شود و می‌تواند با استفاده از همان مدل ریاضی نوسان‌سازهای آرامشی الکترونیکی تجزیه و تحلیل شود. به عنوان مثال، آبفشان‌های زمین گرمایی، شبکه‌های آتش‌کننده سلول‌های عصبی، سیستم‌های گرمایشی کنترل شده با ترموستات واکنش‌های شیمیایی جفت‌شده، تپش قلب انسان زمین‌لرزه‌ها، جیرجیر گچ بر روی تخته‌سیاه، جمعیت چرخه‌ای حیوانات شکارچی و شکار و سامانه‌های فعال‌سازی ژن به عنوان نوسان‌سازهای آرامشی مدل‌سازی شده‌اند. نوسان‌سازهای آرامشی با دو فرایند متناوب در مقیاس‌های زمانی مختلف مشخص می‌شود: یک دوره آرامش طولانی که طی آن سیستم به یک نقطه تعادل نزدیک می‌شود، تناوب با یک دوره تکانشی کوتاه که در آن نقطه تعادل جابجا می‌شود. دوره یک نوسان‌ساز آرامشی عمدتاً توسط ثابت زمان آرامش تعیین می‌شود. نوسان‌سازهای آرامشی نوعی چرخه محدود است و در نظریهٔ کنترل غیرخطی مورد مطالعه قرار می‌گیرد.

نوسان‌سازهای آرامشی الکترونیکی

یک نوسان‌ساز آرامشی مولتی ویبراتور آبراهام-بلوک، فرانسه، ۱۹۲۰ لامپی (جعبه کوچک، سمت چپ). از هارمونیک‌های آن برای کالیبره کردن یک موج سنج (در مرکز) استفاده می‌شود .

نوسان‌ساز مولتی ویبراتور آبراهام-بلوک، لامپی اصلی، از مقاله سال ۱۹۱۹ آنها

اولین مدار نوسان‌ساز آرامشی، مولتی‌ویبراتور آستابل، توسط هنری آبراهام و یوجین بلوک با استفاده از لامپ‌های خلأ در طول جنگ جهانی اول اختراع شد. بالتازار وان دِر پُل برای اولین بار نوسان‌ساز آرامشی را از نوسان‌ساز هارمونیکی متمایز کرد، اصطلاح «نوسان‌ساز آرامشی» را به وجود آورد و اولین مدل ریاضی یک نوسان‌ساز آرامشی، مدل قدرت‌مند نوسان‌ساز وان دِر پُل در سال ۱۹۲۰ به دست آورد. وان دِر پُل اصطلاح آرامش را از مکانیک گرفته‌است. تخلیه خازن مشابه روند آرامش تنش، از بین رفتن تدریجی تغییر شکل و بازگشت به حالت تعادل در یک محیط غیرکشسان است. نوسان‌ساز آرامشی را می‌توان به دو کلاس تقسیم کرد

• نوسان‌ساز دندان‌اره‌ای، جاروب یا فلای‌بک: در این نوع، خازن ذخیره‌کننده انرژی به آرامی شارژ می‌شود اما به سرعت و بلافاصله با اتصال کوتاه از طریق قطعه کلیدزنی تخلیه می‌شود؛ بنابراین فقط یک «سطح شیب دار» در شکل موج خروجی وجود دارد که تقریباً کل دوره تناوب را می‌گیرد. ولتاژ روی خازن یک موج دندان‌اره‌ای است، در حالی که جریان عبوری قطعه کلیدزنی توالی پالس‌های کوتاه است.
• مولتی ویبراتور آستابل: در این نوع، خازن به آرامی از طریق یک مقاومت هم شارژ می‌شود و هم تخلیه می‌شود، بنابراین شکل موج خروجی از دو قسمت تشکیل می‌شود، یک سطح شیب دار افزایشی و یک سطح شیب دار کاهشی. ولتاژ روی خازن یک شکل‌موج مثلثی است، در حالی که جریان عبوری قطعه کلیدزنی یک موج مربعی است.

کاربردها

نوسان‌ساز آرامشی معمولاً برای تولید سیگنال‌های با فرکانس پایین برای کاربردهایی مانند چراغ چشمک زن و بوق الکترونیکی استفاده می‌شوند. و سیگنال‌های ساعت در برخی از مدارهای دیجیتالی. در دوران لامپ خلأ از آنها به عنوان نوسان‌سازها در اندام‌های الکترونیکی و مدارهای انحراف افقی و مبنای‌های زمانی برای اسیلوسکوپ‌های سی‌آرتی استفاده می‌شد. یکی از رایج‌ترین مدارهای انتگرال‌گیر میلر بود که توسط آلن بلوملین اختراع شد، که از لامپ‌های خلأ به عنوان منبع جریان ثابت برای تولید یک شکل‌موج سطح شیب‌دار بسیار خطی استفاده می‌کرد. آنها همچنین در نوسان‌سازهای کنترل شده با ولتاژ (وی‌سی‌او)، اینورترها و منابع تغذیه کلیدزنی، مبدل‌های آنالوگ دیجیتال دو-شیب و در فانکشن ژنراتور برای تولید امواج مربعی و مثلثی استفاده می‌شوند. نوسان‌سازهای آرامشی به‌طور گسترده‌ای مورد استفاده قرار می‌گیرند زیرا طراحی آنها آسان‌تر از نوسان‌سازهای خطی است، ساخت آنها بر روی تراشه‌های مدار مجتمع آسان‌تر است زیرا به سلف‌هایی مانند نوسان‌سازهای LC نیازی ندارند و می‌توان آنها را در محدوده فرکانس وسیعی تنظیم کرد. با این حال آنها دارای نویز فاز بیشتر و پایداری فرکانس ضعیف‌تری نسبت به نوسان‌سازهای خطی هستند. قبل از ظهور میکروالکترونیک، نوسان‌سازهای آرامشی ساده اغلب از یک قطعه مقاومت منفی با پسماند مانند لامپ تایترون، لامپ نئون، یا ترانزیستور تک‌پیوندی استفاده می‌کردند، اما امروزه بیشتر آنها با مدارهای مجتمع اختصاصی مانند تراشه تایمر ۵۵۵ ساخته می‌شوند.

نوسان‌ساز پیرسون-آنسون

نمودار مدار یک اسیلاتور آرامش خازنی با دستگاه آستانه لامپ نئون

این مثال را می‌توان با خازن یا مدار یکپارچه مقاومتی-خازنی که به ترتیب توسط یک منبع جریان یا ولتاژ ثابت و یک قطعه آستانه‌ای با پسماند (لامپ نئون، تایترون، دیاک ، ترانزیستور دو قطبی معکوس-بایاس‌شده، یا ترانزیستور تک‌پیوندی) موازی با خازن متصل شده، ساخت.

اجرای جایگزین با تایمر ۵۵۵

یک نوسان‌ساز آرامشی مشابه را می‌توان با آی‌سی تایمر ۵۵۵ (در حالت بی‌ثبات عمل می‌کند) که جای لامپ نئون بالا را می‌گیرد، ساخت.

اسیلاتور القایی

مبانی اسیلاتور مسدود کننده حالت جامد

یک نوسان‌ساز مهارساز از خواص القایی ترانسفورماتور پالس برای تولید امواج مربعی با راه‌اندازی ترانسفورماتور به حالت اشباع استفاده می‌کند، که سپس جریان تغذیه ترانسفورماتور را تا زمان تخلیه و غیراشباع کردن ترانسفورماتور قطع می‌کند، که پس از آن یک پالس دیگر از جریان تغذیه را می‌چکاند، به‌طور کلی از یک تک ترانزیستور به عنوان عنصر کلیدزنی استفاده می‌شود.

نوسان‌ساز آرامشی برمبنای مقایسه‌گر

یک اسیلاتور پسماندی مبتنی‌بر مقایسه‌گر.

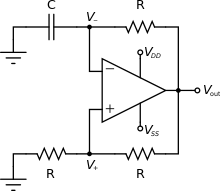
مثال: تحلیل معادلات دیفرانسیل یک نوسان‌ساز آرامشی مبتنی‌بر مقایسه‌گر

تجزیه و تحلیل گذرا از یک نوسان‌ساز آرامشی مبتنی‌بر مقایسه‌گر.

$\,\!V_{+}$ تنظیم شده با $\,\!V_{\rm {out}}$ دوسر مقاومت تقسیم ولتاژ:

$V_{+}={\frac {V_{\rm {out}}}{2}}$

$\,\!V_{-}$ با استفاده از قانون اهم و معادله دیفرانسیل خازن بدست می‌آید:

${\frac {V_{\rm {out}}-V_{-}}{R}}=C{\frac {dV_{-}}{dt}}$

بازنویسی مجدد معادلات دیفرانسیل $\,\!V_{-}$به فرم استاندارد نتایج زیر را ایجاد می‌کند:

${\frac {dV_{-}}{dt}}+{\frac {V_{-}}{RC}}={\frac {V_{\rm {out}}}{RC}}$

توجه داشته باشید که دو جواب برای معادله دیفرانسیل وجود دارد، جواب تحریک شده یا خصوصی و جواب همگن. حل برای جواب تحریک شده، مشاهده کنید که برای این فرم خاص، جواب یک ثابت است. به عبارت دیگر، $\,\!V_{-}=A$ که در آن A ثابت است و ${\frac {dV_{-}}{dt}}=0$ .

${\frac {A}{RC}}={\frac {V_{\rm {out}}}{RC}}$

$\,\!A=V_{\rm {out}}$

با استفاده از تبدیل لاپلاس برای حل معادله همگن ${\frac {dV_{-}}{dt}}+{\frac {V_{-}}{RC}}=0$ منجر می‌شود به

$V_{-}=Be^{{\frac {-1}{RC}}t}$

$\,\!V_{-}$ مجموع جواب خصوصی و همگن است.

$V_{-}=A+Be^{{\frac {-1}{RC}}t}$

$V_{-}=V_{\rm {out}}+Be^{{\frac {-1}{RC}}t}$

حل برای B مستلزم ارزیابی شرایط اولیه است. در زمان ۰ ، $V_{\rm {out}}=V_{dd}$ و $\,\!V_{-}=0$ . جایگزینی در معادله قبلی ما،

$\,\!0=V_{dd}+B$

$\,\!B=-V_{dd}$

فرکانس نوسان

ابتدا بیایید برای سهولت محاسبه فرض کنیم که $V_{dd}=-V_{ss}$ . با نادیده گرفتن شارژ اولیه خازن، که برای محاسبه فرکانس بی‌ربط است، توجه داشته باشید که شارژها و تخلیه‌ها بین ${\frac {V_{dd}}{2}}$ و ${\frac {V_{ss}}{2}}$ است. برای مدار بالا، V_ss باید کمتر از ۰ باشد. نیمی از دوره تناوب (T) همان زمانی است که $V_{\rm {out}}$ از V_dd سوییچ می‌کند. این اتفاق می‌افتد زمانی که V _- شارژ می‌شود از $-{\frac {V_{dd}}{2}}$ به ${\frac {V_{dd}}{2}}$ .

$V_{-}=A+Be^{{\frac {-1}{RC}}t}$

${\frac {V_{dd}}{2}}=V_{dd}\left(1-{\frac {3}{2}}e^{{\frac {-1}{RC}}{\frac {T}{2}}}\right)$

${\frac {1}{3}}=e^{{\frac {-1}{RC}}{\frac {T}{2}}}$

$\ln \left({\frac {1}{3}}\right)={\frac {-1}{RC}}{\frac {T}{2}}$

$\,\!T=2\ln(3)RC$

$\,\!f={\frac {1}{2\ln(3)RC}}$

وقتی V_ss معکوس V_dd نباشد _، باید نگران زمان شارژ و تخلیه نامتقارن باشیم. با در نظر گرفتن این مسئله در نهایت فرمولی از این شکل بدست می‌آوریم:

$T=(RC)\left[\ln \left({\frac {2V_{ss}-V_{dd}}{V_{ss}}}\right)+\ln \left({\frac {2V_{dd}-V_{ss}}{V_{dd}}}\right)\right]$

که منجر به نتیجه فوق می‌شود $V_{dd}=-V_{ss}$ .

جستارهای وابسته

• Multivibrator
• FitzHugh–Nagumo model – A hysteretic model of, for example, a neuron.
• Schmitt trigger – The circuit on which the comparator-based relaxation oscillator is based.
• Unijunction transistor – A transistor capable of relaxation oscillations.
• Robert Kearns – Used relaxation oscillator in intermittent wiper patent dispute.
• Limit cycle – Mathematical model used to analyze relaxation oscillations