قطبش (موجها)
قُطبِش، قُطبیدگی، یا پُلاریزاسیون (به انگلیسی: Polarization)، از ویژگیهای اساسی امواج عرضی است که راستای نوسان موج را در صفحهٔ عمود بر جهت انتشار آن نشان میدهد. در الکترومغناطیس، قطبش یک موج الکترومغناطیسی (مانند نور) نشاندهندهٔ راستای بردارِ میدان الکتریکی آن است.
امواج، قطبشهای متفاوتی دارند؛ قطبش بیضوی، دایرهای (که حالت خاصی از قطبش بیضوی است.) و خطی.
قطبش نور در طبیعت و زندگی روزمره، بیآنکه متوجه باشیم، بسیار به چشم میخورد. مثلاً قطبش نور، اساس کار نمایشگرهای کریستال مایع یا همان اِلسیدی (LCD) است. مواد کریستال مایع، دارای این ویژگی هستند که با اِعمال ولتاژ، میتوانند قطبش نور عبورکننده از خود را تغییر دهند.

انواع قطبش[ویرایش]
امواج طولی (مانند صوت) قطبش ندارند، زیرا راستای نوسان و راستای پیشروی (انتشار) آنها یکی است. در امواج عرضی (مانند نور) راستای نوسان میدان الکتریکی یکتا نیست و با قطبش تعیین میشود.
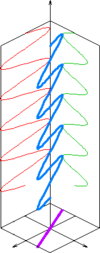
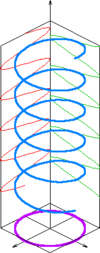
قطبش، عمود بر مسیر حرکت موج الکترومغناطیسی است. ممکن است میدان الکتریکی تنها در یک راستا نوسان کند (قطبش خطی)، یا اینکه راستای نوسانش، مُدام تغییر کند (قطبش چرخشی چپگرد یا راستگرد).
در حالت کلی، قطبش امواج الکترومغناطیسی مسئلهای پیچیدهاست. مثلاً در فیبر نوری یا پرتوهای قطبیده (پلاریزه) در فضای آزاد، توصیف پلاریزاسیون موج پیچیدهتر است، زیرا میدانها، میتوانند تا سه مؤلفه داشتهباشند.
در مواد جامد، امواج صوتی میتوانند به صورت عرضی باشند. در این حالت قطبش با مسیر تنش برشی در سطح عمود بر جهت انتشار در ارتباط است. این موضوع در زلزلهشناسی اهمیت دارد. قطبش در علوم و تکنولوژی در رابطه با انتشار موج اهمیت دارد؛ مثل علوم نوری، مخابرات و رادار.
قطبش نور را میتوان اندازه گرفت.
قطبش موج تخت (Plane wave)[ویرایش]
سادهترین مثال برای قطبش، در امواج تخت (مانند امواج الکترومغناطیسی، از جمله نور) است. در امواج الکترومغناطیسی، میدان الکتریکی و مغناطیسی، عمود بر جهت انتشار و نیز عمود بر یکدیگر نوسان میکنند. در تعیین قطبش، بردار میدان الکتریکی یا مغناطیسی در نظر گرفتهمیشود. برای مثال، میدان الکتریکی یک موج الکترومغناطیسی هارمونیک (تکفرکانس) که در راستای محور منتشر میشود، دو مؤلفهٔ همفرکانس دارد که دامنه و فاز آنها لزوماً یکسان نیستند.
از نظر ریاضی، میدان الکتریکی این موج اینگونه نوشته میشود.
که در آن، یکه موهومی، ثابت نِپِر، بخش حقیقی، عدد موج، و فرکانس زاویهای است؛ بنابراین، میدان الکتریکی ، دو مؤلفهٔ و دارد که دامنهشان به ترتیب و است. این دو مؤلفه، اختلاف فاز دارند، و عبارتند از و .
برای تعیین قطبش، میتوان فرض کرد ، و را برحسب به دست آورد. قطبش این موج الکترومغناطیسی:
- خطی است، اگر .
- دایرهای است، اگر و .
- بیضوی است، اگر و .

نور ناقُطبیده (پُلاریزهنشده)[ویرایش]
نوری که بهطور طبیعی از یک منبع نوری (مانند خورشید) و بدون گذر از هرگونه محیط مادی، یا بازتاب از هر سطح مادی که قطبش آن را تغییر دهد، نور ناقطبیده است.
قطبش در طبیعت، علوم و تکنولوژی[ویرایش]

جستارهای وابسته[ویرایش]
منابع[ویرایش]
- Principles of Optics, 7th edition, M. Born & E. Wolf, Cambridge University, 1999, ISBN 0-521-64222-1.
- Fundamentals of polarized light: a statistical optics approach, C. Brosseau, Wiley, 1998, ISBN 0-471-14302-2.
- Polarized Light, second edition, Dennis Goldstein, Marcel Dekker, 2003, ISBN 0-8247-4053-X
- Field Guide to Polarization, Edward Collett, SPIE Field Guides vol. FG05, SPIE, 2005, ISBN 0-8194-5868-6.
- Polarization Optics in Telecommunications, Jay N. Damask, Springer 2004, ISBN 0-387-22493-9.
- Optics, 4th edition, Eugene Hecht, Addison Wesley 2002, ISBN 0-8053-8566-5.
- Polarized Light in Nature, G. P. Können, Translated by G. A. Beerling, Cambridge University, 1985, ISBN 0-521-25862-6.
- Polarised Light in Science and Nature, D. Pye, Institute of Physics, 2001, ISBN 0-7503-0673-4.
- Polarized Light, Production and Use, William A. Shurcliff, Harvard University, 1962.
- Ellipsometry and Polarized Light, R. M. A. Azzam and N. M. Bashara, North-Holland, 1977, ISBN 0-444-87016-4
- Secrets of the Viking Navigators—How the Vikings used their amazing sunstones and other techniques to cross the open oceans, Leif Karlsen, One Earth Press, 2003.
| در ویکیانبار پروندههایی دربارهٔ قطبش (موجها) موجود است. |



![{\displaystyle {\vec {E}}(x,y,z,t)=\mathrm {Re} \left[\left(A_{x},A_{y}e^{i\phi },0\right)e^{i(kz-\omega t)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdca570c3b22ed3ebc039fad35cb6a05b1697b09)


![{\displaystyle {\rm {{Re}[\cdot ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6296f16d5ff3d910708659af87164e6d5afc5930)