منحنی جرونو
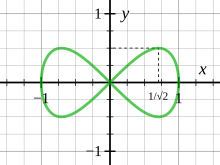
در هندسه جبری منحنی جرونو، (به انگلیسی: lemniscate of Gerono) یا (به انگلیسی: lemniscate of Huygens) یک منحنی جبری صفحهای، تجزیپذیر به صفر و درجه چهارم است. شکل منحنی شبیه عدد هشت لاتین یا علامت بینهایت ریاضی است. معادله آن به شرح زیر است:
این منحنی برای نخستین بار به وسیله کمیل کریستوفر جرونو پیشنهاد و طراحی شده است.
به دلیل معادل بودن این معادله با صفر میتوان آن را یک تابع منطقی یا استدلالی توصیف کرد. یعنی میتوان نوشت:
همچنین:
منحنی جرونو مورد ویژهای از منحنی لیساژو است.
منابع[ویرایش]
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. ۱۲۴. ISBN 0-486-60288-5.






