از ویکیپدیا، دانشنامهٔ آزاد
در هندسهٔ تحلیلی ، رویههای درجهٔ دوم در فضای سهبعدی دستهای از رویهها هستند که به این صورت تعریف میشوند: مکان هندسی همهٔ نقاطی مانند
P
=
(
x
,
y
,
z
)
{\displaystyle P=(x,y,z)}
F
(
x
,
y
,
z
)
=
0
{\displaystyle F(x,y,z)=0}
F
{\displaystyle F}
تابع درجهٔ دو است.[۱]
به عنوان مثال کُره یک رویهٔ درجه دو است؛ زیرا معادلهٔ استاندارد کره یک معادلهٔ درجه دو است:
x
2
+
y
2
+
z
2
=
r
2
{\displaystyle x^{2}+y^{2}+z^{2}=r^{2}}
بهطور کلّیتر، ابررویههای درجه دو در فضای
R
n
{\displaystyle \mathbb {R} ^{n}}
ابررویههای
n
−
1
{\displaystyle n-1}
P
=
(
x
1
,
x
2
,
…
,
x
n
)
{\displaystyle P=(x_{1},x_{2},\dots ,x_{n})}
F
(
x
1
,
x
2
,
…
,
x
n
)
=
0
{\displaystyle F(x_{1},x_{2},\dots ,x_{n})=0}
F
{\displaystyle F}
تابع درجهٔ دو است.
در نتیجه میتوان مقاطع مخروطی را حالت خاصی از رویههای درجه دو (حالت
n
=
2
{\displaystyle n=2}
فضای دوبعدی به جای «رویه » باید از اصطلاح «خم » استفاده کرد.
در فضای سهبعدی، رویههای درجه دو به شاخههای زیر تقسیم میشود:[۱]
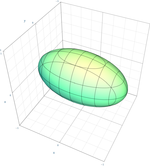
بیضیگون
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,}
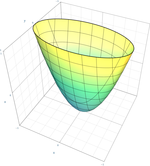
سهمیگون بیضوی
x
2
a
2
+
y
2
b
2
=
z
c
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}={z \over c}\,}
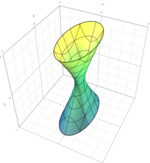
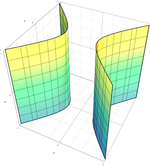
سهمیگون هذلولوی
x
2
a
2
−
y
2
b
2
=
z
c
,
c
>
0
{\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}={z \over c},\quad c>0\,}
هذلولیگون یکپارچه
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,}
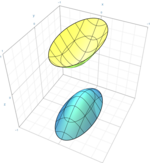
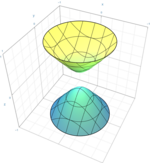
هذلولیگون دوپارچه
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
−
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1\,}
حالات حدّی یا تبهگنی
مخروط بیضوی
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,}
استوانهٔ بیضوی
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}
استوانهٔ هذلولوی
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,}
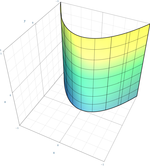
استوانهٔ سهموی
x
2
+
2
a
y
=
0
{\displaystyle x^{2}+2ay=0\,}
وقتی که دو یا هر سه ثابت (
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
رویهٔ درجه دو دورانی به دست میآید:
حالات خاص: رویهٔ دورانی
کرهگون
x
2
a
2
+
y
2
a
2
+
z
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}=1\,}
کره
x
2
+
y
2
+
z
2
=
r
2
{\displaystyle x^{2}+y^{2}+z^{2}=r^{2}\,}
سهمیگون دایروی
x
2
a
2
+
y
2
a
2
−
z
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,}
هذلولیگون دورانی یکپارچه
x
2
a
2
+
y
2
a
2
−
z
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=1\,}
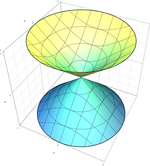
هذلولیگون دورانی دوپارچه
x
2
a
2
+
y
2
a
2
−
z
2
b
2
=
−
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=-1\,}
سطح مخروطی
x
2
a
2
+
y
2
a
2
−
z
2
b
2
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=0\,}
استوانه (دایروی)
x
2
a
2
+
y
2
a
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1\,}
جستارهای وابسته [ ویرایش ]
↑ ۱٫۰ ۱٫۱ «۱۲٫۶». Thomas' Calculus (14th Edition) .