تابع هش رمزنگاری

نحوه کار عملی یک تابع درهمک‌ساز رمزنگاری (مخصوصا SHA1). یک تغییر کوچک در ورودی (در واژه "over") به شدت خروجی (درهمک یا چکیده) را تغییر داده‌است. به این موضوع اثر بهمنی گفته می‌شود.

الگوریتم های ایمن درهم‌ساز
مفاهیم
توابع درهم‌ساز · اس‌اچ‌ای · دی‌اس‌اِی
استانداردهای اصلی
اس‌اچ‌ای۰ · اس‌اچ‌ای۱ · اس‌اچ‌ای۲ · اس‌اچ‌ای-۳

تابع هش رمزنگاری (CHF) (به انگلیسی: Cryptographic hash function) یک الگوریتم ریاضی است که داده‌هایی با اندازه اختیاری (به آن «پیام» گفته می‌شود) را به یک آرایه بیتی با اندازه ثابت (به آن «درهَمَک»، «هش» یا «چکیده پیام» گفته می‌شود) نگاشت می‌دهد. ویژگی مهم این تابع «یک‌طرفه بودن» آن است و این یعنی تابعی است که وارون‌سازی آن از نظر عملی اجراپذیر نیست. از نظر ایدئال تنها روش یافتن پیامی که یک هش معین را ساخته‌است، انجام یک جستجوی غیرهوشمندانه روی همه ورودی‌های ممکن است تا ببینیم که آیا همخوانی دارند یا نه، روش دیگر استفاده از یک جدول رنگین‌کمانی از درهمک‌های همخوان است. توابع درهمک‌ساز رمزنگاری، یکی از ابزارهای اساسی در رمزنگاری مدرن هستند.

یک تابع درهمک‌ساز رمزنگارانه به صورت ایدئال دارای این ویژگی‌های اصلی است:

• قطعی است، یعنی یک پیام یکسان، همیشه منجر به یک درهمک مشابه می‌شود.
• عمل محاسبه مقدار درهمک برای هر پیام معین «سریع» است.
• ایجاد پیامی که یک درهمک معین را تولید کرده‌است غیرقابل اجرا است. (یعنی نمی‌توان فرایندی که یک مقدار درهمک معین را تولید کرده‌است را معکوس‌سازی کرد).
• یافتن دو پیام متفاوت که یک مقدار درهمک مشابه دارند، غیر اجرایی است.
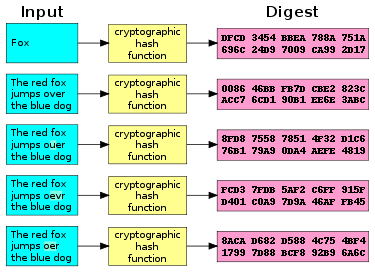
• یک تغییر کوچک در پیام، باید مقدار درهمک را به آن‌اندازه گسترده تغییر دهد که مثل آن باشد که یک مقدار درهمک جدیدی پدیدار شده، که این درهمک با مقدار درهمک قدیمی ارتباطی ندارد (که به آن اثر بهمنی گفته می‌شود).

توابع درهمک‌ساز رمزنگاری، کاربردهای زیادی در امنیت اطلاعات دارند، به ویژه آن‌ها در امضای دیجیتال، کدهای احرازهویت پیام (MACs)، و دیگر حالت‌های احرازهویت کاربرد دارند. از این توابع می‌توان به عنوان توابع درهمک‌ساز ساده استفاده کرد، یعنی در اندیس‌دهی به داده در جداول درهمک، برای اثرانگشت‌دهی، برای تشخیص داده تکراری، یا برای تشخیص یکتای فایل‌ها، و به عنوان جمع‌آزما برای تشخیص خرابی تصادفی داده استفاده می‌شود. در واقع در زمینه امنیت رایانه، به مقادیر درهمک رمزنگارانه، اصطلاحات «اثرانگشت دیجیتالی»، «جمع‌آزما»، یا فقط «مقادیر درهمک» هم گفته می‌شود، اگرچه همه این اصطلاحات برای توابع «عمومی‌تر» هستند که ویژگی‌ها و اهداف متفاوتی را دارند.

ویژگی‌ها

اکثر توابع درهم ساز رمزنگارانه برای بدست آوردن رشته ای با هر طولی به عنوان ورودی و تولید یک مقدار درهم با طول ثابت طراحی می‌شوند.

تابع درهم ساز رمزنگارانه باید قادر به رویارویی با همه نوع حملات کشف نوشته رمزی باشد. در رمزنویسی نظری، سطح امنیت تابع درهم ساز رمزنگارانه با استفاده از مشخصه‌های زیر تعریف می‌شود:

- مقاومت در برابر تصویر اولیه و پردازش نشده

با توجه به مقدتر مشخص هش h، پیدا کردن پیام m مثل h=hash(m) باید مشکل باشد. این مفهوم به تابع یک سویه ارتباط پیدا می‌کند. توابعی که از این ویژگی برخوردار نباشند، نسبت به حملات تصویر اولیه و پردازش نشده آسیب‌پذیر هستند.

- مقاومت در برابر تصویر پردازش نشده دوم

با توجه به مقدار ورودی m1، پیدا کردن ورودی متفاوت m2 باید مشکل باشد با تساوی مقابل: hash(m1) = hash(m2). این ویژگی بعضاً "مقاومت تصادم ضعیف نامیده می‌شود. توابعی که از این ویژگی برخوردار نباشند، نسبت به حملات تصویر پردازش نشده دوم آسیب‌پذیر هستند.

- مقاومت برخورد

پیدا کردن دو پیام متفاوت m1 و m2 با در نظر گرفتن تساوی hash(m1) = hash(m2) مشکل است. این جفت «برخورد هش رمزنگاری نامیده می‌شوند». این ویژگی بعضاً «مقاومت قوی در برابر برخورد» اطلاق می‌شود. حداقل نیاز به مقدار هش دو برابر اولیه دارد تا اینکه به مقاومت تصویر پردازش نشده دست پیدا کند. در غیر اینصورت برخوردها می‌توانند جزو حمله روز تولد (حمله ای بدون تغییر معنی اولیه مورد حمله شده) طبقه‌بندی شوند (۴).

مقاومت در برابر برخورد، دلالت ضمنی بر مقاومت تصویر اولیه و پردازش نشده دوم دارد، اما نه مقاومت اولیه آن (۵). فرضیه ضعیف تر همیشه در رمزنگاری نظری غالب است، اما عملاً، تابع درهمی که تنها مقاومت در برابر تصویر پردازش نشده دوم است، ناامن تلقی شده و در این صورت برای کاربردهای واقعی توصیه نمی‌شود.

این ویژگی‌ها غیررسما، به این معنی هستند که «دشمن یا رقیب متخاصم» نمی‌تواند بدون تغییر چکیده داده ورودی، آن جایگزینش شده یا آن را تغییر دهد؛ بنابراین، اگر دو رشته دارای یک چکیده یکسان باشند، می‌توان اطمینان حاصل کرد که آنها باهم برابرند. مقاومت در برابر تصویر خام پردازش نشده دوم، از دستکاری کردن سند توسط حمله کننده با یک هش یکسان جلوگیری می‌کند. مقاومت در برابر برخورد از ایجاد دو سند متمایز توسط حمله کننده با یک هش مشابه جلوگیری می‌کند.

تابعی که از این معیارها برخوردار باشد، هنوز هم دارای ویژگی‌های نامناسبی خواهد بود. در حال حاضر، پرطرفدارترین توابع درهم ساز رمزنگارانه، نسبت به حملات «کششی-طول» آسیب‌پذیر هستند: با در نظر گرفتن hash(m) و len(m) اما نه m، با انتخاب m مناسب، حمله کننده می‌تواند تابع درهم hash(m ∥ m′) را محاسبه کند، در اینجا منظور از ∥ الحاق است (۶). از این ویژگی می‌توان برای ترسیم الگوهای سندیت بخشی ساده بر مبنای توابع درهم استفاده کرد. سازه HAMC روشی است برای غلبه بر این مشکلات.

عملاً مقاومت در برابر برخورد، در خیلی از کاربردهای عملی کافی بنظر نمی‌رسد. علاوه بر مقاومت در برابر برخورد، باید پیدا کردن دو پیام با چکیده یا خلاصه‌های کاملاً مشابه توسط رقیب، غیرممکن باشد، یا استنباط هر گونه اطلاعات مفید در مورد داده‌ها. به‌ویژه، تابع درهم باید تا حد ممکن مثل «تابع تصادفی» عمل کند (که در گواه امنیتی، اوراکل تصادفی نامیده می‌شود) در عین حال از نظر محاسباتی قطعی و مؤثر باشد. این توابعی مثل تابع SWIFFT را غیرمحتمل می‌شمارد، و اثبات شده که می‌تواند مقاومت برخورد داشته باشد بااین فرض که مسائل معین روی شبکه‌های ایدئال، به سختی قابل محاسبه هستند، اما در قالب تابع خطی این ویژگی‌های اضافی قابل پوشش دادن نیستند (۷).

الگوریتم‌های مجموع مقابله ای یا جمع کنترلی، مثل CRC32 و سایر کنترل‌های افزونگی دوره ای برای پوشش دادن الزامات ضعیف تر طراحی می‌شوند و به‌طور کالی مناسب توابع درهم ساز رمزنگارانه نیستند. برای مثال، CRC برای یکپارچه سازی پیام طبق استاندارد رمزنویسی VEP استفاده شد، امادر یک حمله می‌توان راحتی از حالت خطی جمع کنترلی خبر دار شد.

درجه سختی

در عمل رمزنویسی، به‌طور کلی غیرمحتمل است که تقریباً اطمینان بدست آورد که رقیب یا دشمن به اطلاعات دسترسی پیدا نخواهد کرد باید تا زمانی که فرض می‌شود امنیت سیستم از اهمیت حیاتی برخوردار است، از ورود او به سیستم باید جلوگیری کرد؛ بنابراین، مفهوم این اصطلاح تاحدی به کاربردش بستگی دارد از آنجاییکه کاری که یک عامل خطرناک یا متخاصم انجام می‌دهد معمولاً به نسبت سود مورد انتظارش از این کار سنجیده می‌شود. هر چند، از آنجاییکه معمولاً تلاش مضاعف برای دست پیدا کردن به پیامی با طول چکیده مضاعف است، حتی مزیت چندین برابر در قدرت پردازش با اضافه کردن بیت‌های متعدد به حروف، می‌تواند خنثی شود.

برای پیام‌های انتخاب شده از مجموعه پیام‌های محدود، مثلاً رمز عبور یا دیگر پیام‌های کوتاه، تبدیل هش با سری قرار دادن پیام‌ها، عملی می‌باشد. بخاطر اینکه معمولاً توابع درهمه ساز رمزنگارانه برای محاسبه سریع طراحی می‌شوند، توابع مشتق کلیدی ویژه که مستلزم وجود منابع محاسباتی بیشتری هستند، پای کار می‌آیند که موفقیت چنین حملات جستجوی فراگیر را مشکل‌تر می‌سازند.

در برخی از تحلیل‌های نظری، «مشکل یا سخت» به معنی ریاضی خاصی است، مثل «غیرقابل حل در زمان چندجمله ای مجانب». این تفسیر راجع به سختی و مشکل، در مطالعه «توابع درهم ساز رمزنگارانه امنیت قابل اثبات» مهم می‌باشد اما معمولاً ارتباطی قوی با امنیت عملی ندارد. برای مثال، الگوریتم «زمان نموی» بعضاً بریا حمله احتمالی خیلی سریع می‌باشد. بالعکس، الگوریتم زمان چندجمله ای (الگوریتمی که مستلزم وجود n20 مرحله برای کلیدهای n-رقمی است) ممکن است برای استفاده عملی خیلی آهسته باشد.

تصویر سازی

تصویرسازی استفاده بالقوه از درهم ساز رمزنگاری به شرح زیر است: آلیس، یک مسئله ریاضی دشوار را برای باب مطرح کرد و ادعا کرد که او را حل کرده‌است. باب دوست داشت خودش آن را حل کند، اما مطمئن بود که آلیس بلوف نمی‌زند؛ بنابراین، آلیس راه حل خودش را نوشت، هش آن را محاسبه کرد و به باب گفت که مقدار هش چقدر است (درحالیکه راه حل آن را به او نگفت). سپس، وقتی که باب راه حل خودش را چند روز بعد به او گفت، آلیس می‌توانست ثابت کند که راه حل او اول ارائه شده و باب آن را درهم کرده‌است و آن را چک کرد تا مقدار هشی که قبلاً بدست آورده بود با مقدار هش محاسبه شده او مطابقت داشته باشد. (این یک نمونه از الگوی سپارش ساده است. در واقعیت، آلیس و باب یک برنامه کامپیوتری هستند و راز چیزی خواهد بود که کمتر از یک راه حل معمای ادعا شده قابل تقلب باشد).

کاربردها

تأیید صحیح بودن یا یکپارچه بودن پیام‌ها و فایل‌ها

یک کاربرد مهم هش‌های امنیتی، تأیید صحیح و یکپارچه بودن پیام‌ها است. مقایسه چکیده‌های پیام (چکیده‌های هش در برابر پیام) محاسبه شده قبل و بعد از ارسال می‌تواند مشخص کند که آیا تغییراتی روی پیام یا فایل صورت گرفته یا نه.

چکیده‌های هش MD5, SHA1 یا SHA2 بعضاً روی وب سایت‌ها برای تأیید درستی فایل‌های دانلود شده منتشر می‌شوند (۸)، که شامل فایل‌های بازیابی شده با استفاده از «به اشتراک گذاری فایل» مثل «معکوس نمودن» می‌شود. این عمل یک زنجیره اطمینان می‌سازد تا زمانیکه هش‌ها روی سایت مطمئنی پست شوند- معمولاً سایتی که با پسوند معتبر HTTPS تأیید شود. با استفاده از تابع درهم ساز رمزنگاری و زنجیره اطمینان، تغییرات خطرناک فایل تشخیص داده می‌شوند. سایر «کدهای تشخیص خطا» مثل «کنترل افزونگی دوره ای» تنها از تغییرات غیرخطرناک فایل جلوگیری به عمل می‌آورند.

تولید امضاء و تأیید آن

تقریباً همه الگوهای امضاء دیجیتالی نیاز به هش رمزنگاری جهت محاسبه پیام دارند. این کار امکان محاسبه امضاء با چکیده هش نسبتاً کوچک و با اندازه ثابت را فراهم می‌کند. پیام در صورتی معتبر و صحیح عنوان می‌شود که تأیید امضاء تصدیق شود و چکیده هش مجدداً محاسبه شده پیام وجود داشته باشد؛ بنابراین، ویژگی صحیح بودن پیام هش رمزنگاری، برای تولید الگوهای امضاء دیجیتالی امن و مؤثر استفاده می‌شود.

تأیید رمز عبور

تأیید «رمز عبور» معمولاً وابسته به هش‌های رمزنگاری است. ذخیره کردن همه رمزهای عبور به شکل «متن پاک یعنی پیام بدون رمز» می‌تواند به اخلال امنیتی گسترده‌ای منجر شود، اگر فایل رمز عبوری افشا شود. یک روش برای کاهش این خطر، تنها ذخیره کردن چکیده هش رمز عبور است. برای به رسمیت شناختن کاربر، رمز عبوری ارائه شده توسط کاربر، به‌صورت درهم درآمده و با هش ذخیره شده مقایسه می‌شود. روش بازیابی رمز عبور زمانی ضرورت دارد که درهم کردن رمز عبور انجام شود. رمزهای عبوری اصلی را نمی‌توان از مقدار هش ذخیره شده مجدداً محاسبه کرد.

توابع درهم ساز رمزنگاری استاندارد، برای محاسبه سریع طراحی می‌شوند و در نتیجه حدس زدن رمز عبور با سرعت بالا امکان‌پذیر خواهد بود. "واحدهای پردازش گرافیکی" می‌توانند میلیاردها رمز عبوری در هر ثانیه تولید کنند. توابع درهم رمز عبور که کار "امتداد کلید" را انجام می‌دهند- مثل PUKDF2، دست نوشته متنی یا Argon2- معمولاً از نوآوری‌های متعدد درهم رمزنگاری برای افزایش زمان (در برخی موارد حافظه کامپیوتر) مورد نیاز برای انجام "حملات بروت فورس یا جستجوی فراگیر روی چکیده‌های درهم رمز عبوری ذخیره شده استفاده می‌کنند. هش رمز عبور مستلزم وجود یک مقدار salt غیر محرمانه و تصادفی بزرگ می‌باشد تا بتوان آن را با هش رمز عبور ذخیره کرد. salt خروجی هش رمز عبور را به‌صورت تصادفی درمی‌آورد، و امکان ذخیره‌سازی جداول رمز عبور را برای رقیب یا دشمن غیرممکن می‌سازد هم چنین مقادیر هش از پیش محاسبه شده را که در آن‌ها چکیده هش رمز عبور را می‌توان مقایسه کرد.

خروجی تابع درهم رمز عبور نیز می‌تواند به عنوان کلید رمزنگاری استفاده شود. توابع هش رمز عبور نیز به عنوان "توابع مشتق کلید " مبتنی بر رمز عبور شناخته می‌شوند (PBKDF).

اثبات کار

سیستم اثبات کار (یا پروتکل یا تابع) یک مقیاس سنجش اقتصادی برای تشخیص حملات «رد خدمات» یا دیگر سوء استفاده‌های سرویسی مثل اسپم روی شبکه با درخواست کننده سرویس است که معمولاً زمان پردازش کامپیوتر را تغییر می‌دهد. یک مشخصه اصلی این الگوها، نامتقارنی آنهاست: کار باید از سمت درخواست کننده نسبتاً سخت (اما امکان‌پذیر) باشد اما چک کردن آن توسط ارائه دهنده خدمات باید راحت باشد. یک سیستم پرطرفدار که در داده کاوی بیتکوین و Hashcash استفاده می‌شود- از معکوس تابع درهم جزئی برای اثبات کار انجام شده و برای تعیین پاداش داده کاوی در بیتکوین به عنوان توکن یا کلمه رمزی اعتبار کار برای ارسال ایمیل در Hashcash بکار گرفته می‌شود. فرستنده، باید یک پیامی را پیدا کند که مقدار هش آن با عدد بیت صفر شروع می‌شود. کار متوسطی که فرستنده باید برای پیدا کردن پیام معتبر انجام دهد، در تعداد بیت صفر مورد نیاز در مقدار هش، به‌صورت نمایی است، درحالیکه دریافت کننده می‌تواند صحت پیام را با اجرای یک تابع درهم واحد تأیید کند. برای نمونه، در Hashcash، فرستنده درخواست تولید سر پیام می‌کند که در آن مقدار هش 160 bit SHA-۱ دارای ۲۰ بیت اول به صورت صفر است. به‌طور متوسط فرستنده کار 2¹⁹ برابر برای پیدا کردن سر پیام معتبر انجام می‌دهد.

شناساگر فایل یا داده

چکیده پیام نیز به عنوان ابزاری برای شناسایی معتبر یک فایل استفاده می‌شود. چند سیستم «مدیریت رمز سورس» مثل Git, Mercurial, Monotone از sha1sum انواع مختلف محتوا (محتوای فایل، درخت‌های راهنما، اطلاعات پیشینیان و غیره) برای شناسایی تک به تک آنها استفاده می‌کنند. هش‌ها برای شناسایی فایل‌ها روی شبکه‌های به اشتراک گذاری فایل ههمتا استفاده می‌شوند. برای مثال، در لینک ed2k، تابع درهم متغیر-MD4 با اندازه فایل ترکیب می‌شود و اطلاعات کافی برای پیدا کردن مکان سورس‌های فایل، دانلود فایل و تأیید محتوای آن فراهم می‌کند. «لینک‌های مگنت» مثال دیگری از این دست می‌باشند. این هش‌های فایل بیشتر هش بالا «فهرست هش» یا «درخت هش» هستند که مزایای زیادی دارند.

یکی از کاربردهای اصلی «تابع درهم» جستجوی سریع داده در «جدول درهم» است. توابع درهم رمزنگار بعنوان توابع درهم از یک نوع خاص، خودشان کاربردهای متنوعی دارند.

هرچند، در مقایسه با توابع درهم استاندارد، توابع درهم ساز رمزنگارانه، هزینه محاسبات بالایی دارند. بهمین دلیل، آنها در زمینه‌هایی کاربرد دارند که در آنها حفاظت کاربران در برابر جعل اسناد و امضاء سازی (تولید داده با یک چکیده به شکل داده مد نظر) ضروری می‌باشد.

توابع درهم بر مبنای رمزنگاری بلوکی

چند روش برای استفاده از «رمزنگاری بلوکی» برای ساخت تابع درهم ساز رمزنگار به‌ویژه «تابع فشرده یک سویه» وجود دارد.

این روش‌ها شبیه «حالت‌های عملیات رمز بلوکی» استفاده شده برای رمزنویسی می‌باشند. بسیاری از توابع درهم معروف مثل MD4, MD5, SHA-1 و SHA-2 از مولفه‌های رمزنگار بلوکی-مانند طراحی شده برای این منظور ساخته می‌شوند، با این بازخورد تا اطمینان حاصل شود تابع حاصله معکوس پذیر نیست. شرکت کننده‌های SHA-3 در مرحله نهایی شامل توابعی با مولفه‌های «رمزنگار بلوکیک-مانند» (Skein, BLAKE) می‌باشند، در عین حال تابع نهایی انتخاب شده Keccak روی ابر رمزنگار ساخته شده بود.

رمزنگار بلوکی استاندارد مثل AES را می‌توان در محل این رمزهای بلوکی معمول استفاده کرد و زمانی مثمرثمر می‌باشد که «سیستم الحاقی یا جانمایی شده داخل آن» نیاز به اجرای هم رمزنویسی و هم درهم سازی با اندازه کد کمینه یا ناحیه سخت‌افزار داشته باشد. هرچند، این روش برای راندمان و امنیت بالاتر هزینه بالایی می‌طلبد. حروف رمزی در توابع درهم برای درهم سازی ساخته می‌شوند: آنها از کلیدها و بلوک‌های بزرگ استفاده می‌کنند، می‌توانند کلیدها را برای هر بلوک به خوبی تغییر دهند و برای مقاومت در برابر «حملات کلید-مربوط» طراحی و انتخاب شوند. حروف رمزی هدف-کلی دارای اهداف طراحی متفاوتی هستند. به‌ویژه، AES دارای اندازه کلید و بلوکی می‌باشد که استفاده از آن را برای تولید مقادیر هش طولانی غیر بدیهی می‌سازد. رمزنویسی AES وقتی عملکردش ضعیف تر می‌شود که کلید هر بوک را تغییر دهد و حمله کلید-مربوط استفاده از آن را در تابع درهم در مقایسه با رمزنویسی، کم ایمن تر سازد.

طراحی تابع درهم

سازه Merkle–Damgård

تابع درهم باید قادر به پردازش پیام طول-مورد نظر خود به خروجی-طول ثابت باشد. این کار با تقسیم کردن ورودی به سری بلوک‌هایی با اندازه برابر و عملیات روی آنها به‌صورت متوالی با استفاده از «تابع فشرده یک سویه» انجام می‌شود. به‌ویژه تابع فشرده را می‌توان برای درهم سای یا ساختن از رمزنگاری بلوکی طراحی کرد. تابع درهم ساخته شده از سازه Merkle–Damgård مقاوم به برخورد است از آنجاییکه یک تابع فشرده محسوب می‌شود. هر گونه برخورد برای تابع درهم کامل را می‌توان برخورد در تابع فشرده دانست.

آخرین بلوک پردازش شده نیز باید به‌طور واضح بر اساس "طول لایه گذاری شده باشد". این کار برای امنیت سازه از اهمیت بسزایی برخوردار است. این سازه "سازه Merkle–Damgård" نامیده می‌شود. متداول‌ترین توابع درهم قدیمی مثل SHA-1 و MD5 به این نحو می‌باشند.

لوله پهن در برابر لوله باریک

کاربرد ساده سازه فوق که در آن اندازه خروجی هش برابر است با اندازه حالت داخلی (بین هر مرحله فشرده سازی)، به طراحی هش "لوله یا میله-باریک" منجر می‌شود. این طراحی دارای عیب‌های ذاتی متعددی می‌باشد، مثل "کشیده کردن طول"، چند برخوردی (۹)، حملات پیام طولانی (۱۰)، حملات تولید و paste، ولی نمی‌توانند جفت یا برابر شوند. در نتیجه، توابع درهم پیشرفته روی سازه لوله-پهن ساخته می‌شوند که دارای اندازه حالت داخلی بزرگتری است- و دامنه آن از پیچ ساه فوق تا سازه‌های جدید نظیر "سازه ابر" و سازه HAIFA گستر ده شده‌است (۱۱). هیچ‌یک از ورودی‌های "رقابت تابع درهم NIST" از سازه قدیمی Merkle–Damgård استفاده نمی‌کنند.

در ضمن، کوتاه سازی خروجی هش طولانی، مثل خروجی استفاده شده در SHA-512/256 نیز در برابر حملات متعددی دفاع می‌کند (۱۳).

استفاده برای ساخت سایر واحد اولیه رمزنگاری

توابع درهم را می‌توان برای ساخت سایر واحدهای اولیه رمزنگاری استفاده کرد. برای امن بودن این واحدها از نظر رمزنگاری، برای ساختن درست آنها باید دقت زیادی خرج کرد.

«کدهای تأیید پیام» (MAC) (که توابع درهم کلیدی نیز نامیده می‌شوند) اغلب از توابع درهم ساخته می‌شوند. HAMC مثل MAC است.

درست مثل "رمزنگارهای بلوکی که می‌توانند برای ساخت توابع درهم استفاده شوند، توابع درهم را می‌توان برای ساخت رمزهای بلوکی استفاده کرد. ساخت Luby-Rackoff با استفاده از توابع درهم را زمانی می‌توان ایمن تلقی کرد که توابع درهم اصلی ایمن باشند. هم چنین، بسیاری از توابع درهم ساز (مثل SHA-1 و SHA-2) با استفاده از رمزنگاری بلوکی با یک هدف-ویژه در سازه Davies–Meyer یا سازه دیگر ساخته می‌شوند. هم چنین از حروف رمزی می‌توان در حالت عملیات رایج بدون تضمین امنیت یکسان استفاده کرد. به SHACAL, BEAR و LION مراجعه کنید.

«سازنده‌های عدد تصادفی ساختگی» (PRNG) را می‌توان با استفاده از توابع درهم ساخت. این کار با بنیان تصادفی (رمزی) با شمارنده و درهم کردن آن انجام داد.

برخی از توابع درهم نظیر Skein, Keccak و RadioGatún یک دنباله یا مسیر طولانی اختیاری را تولید می‌کنند و می‌توانند به عنوان «رمزهای دنباله ای» استفاده شوند. هم چنین رمزهای دنباله ای را می‌توان از از توابع درهم با چکیده طول-ثابت استفاده کرد. اغلب این کار با اولین ساخت «سازنده اعداد تصادفی ساختگی امن از نظر رمزنگاری» و سپس با استفاده از دنباله بایت‌های تصادفی مثل keystream انجام می‌شود. SEAL یک رمزنگار دنباله ای است که از SHA-1 برای تولید جداول داخلی استفاده می‌کند و سپس در سازنده keystream بکار گرفته می‌شود که به الگوریتم درهم مرتبط یا غیرمرتبط است. SEAL را نمی‌توان مثل SHA-1 قوی یا ضعیف تضمین کرد. به‌طور مشابه، گسترش کلید رمزنگارهای دنباله ای HC-128 و HC-256 استفاده زیاد از تابع درهم SHA-256 را به دنبال دارد.

الحاق

خروجی‌های «الحاقی» از چند تابع درهم، مقاومت به برخورد را به خوبی قوی‌ترین الگوریتم‌ها با نتایج بهم پیوسته ایجاد می‌کنند. برای مثال، نسخه‌های قدیمی امنیت لایه انتقال (TLS) و لایه سوکت‌های امنیتی (SSL) از مجموع بهم پیوسته MD5 و SHA-1 استفاده می‌کنند (۱۴٫۱۵). این کار تضمین می‌کند که روش شنسایی برخورد در یکی از توابع درهمه، از داده‌های حفاظت شده توسط هر دو تابع درهم را مانع نمی‌شود.

برای توابع درهم "سازه Merkle–Damgård"، تابع الحاقی به مانند قوی‌ترین مولفه، مقاوم به برخورد است، اما نه خیلی پایدار. Antoine Joux مشاهده کرد که ۲-برخورد به n-برخورد می‌انجامد: اگر حمله کننده بتواند دو پیام با یک هش مشابه MD5 را پیدا کند، می‌تواند بسیاری از پیام‌های مورد نظر خود را با هش‌هایی با MD5 یکسان بدون هیچ مشکلی پیدا کند (۱۶). از بین پیام‌های n با تابع درهم مشابه MD5، احتمالاً یک برخورد در SHA-1 وجود دارد. کار بیشتری برای پیدا کردن برخورد SHA-1 لازم است که تنها می‌توان از زمان چندجمله ای برای آن استفاده کرد.

الگوریتم‌های درهم ساز رمزنگارانه

الگوریتم‌های درهم ساز رمزنگاری متعددی وجود دارند. در این قسمت چند الگوریتم را شرح می‌دهیم که نسبتاً کاربردهای زیادی دارند. فهرست بزرگتر آن را می‌توان در صفحه حاوی «مقایسه توابع درهم ساز رمزنگاری» جستجو کرد.

MD5

MD5 توسط Ronald Rivest در سال ۱۹۹۱ برای جایگزین کردن آن با تابع درهم اولیه MD4 طراحی شده بود و در سال ۱۹۹۲ به عنوان RFC 1321 معرفی شد. برخوردها در برابر MD5 را می‌توان در چند ثانیه محاسبه کرد که باعث می‌شود این الگوریتم در اکثر موارد کابرد مناسبی نداشته باشد در اینجا به تابع درهم رمزنگاری احتیاج داریم. MD5 چکیده ۱۲۸ بیتی تولید می‌کند (۱۶ بایت).

SHA-1

SHA-1 به عنوان بخشی از پروژه «اصلی» دولت آمریکا معرفی شده بود. مشخصه اصلی آن که در حال حاضر با SHA-0 شناخته می‌شود- الگوریتمش در سال ۱۹۹۳ تحت استاندارد هش امن، FIPS PUB 180 توسط نهاد استاندارد دولتی آمریکا NIST (مؤسسه ملی استاندارد و فناوری) منتشر شده بود. مدت کوتاهی بعد از انتشار آن توسط NSA رد شد و با نسخه بازبینی شده (تجدید نظر شده) آن جایگزینش شد و در سال ۱۹۹۵ در FIPS PUB 180-1 چاپ شد و با SHA-1 شناخته شد. برخورد در برابر الگوریتم کامل SHA-1 را می‌توان با استفاده از «حمله خرد شده» تولید کرد و باید تابع درهم را شکسته در نظر گرفت. SHA-1 چکیده درهم ۱۶۰بیتی (۲۰ بایتی) تولید می‌کند.

اسناد را می‌توان درست مثل “SHA”، SHA-1 اطلاق کرد، حتی با وجودی که ممکن است با سایر الگوریتم‌های درهم استاندارد مثل SHA-0, SHA-2 و SHA-3 در تضاد باشد.

RIPEMD-160

RIPEMD (چکیده پیام ارزیابی اولیه یکپارچه RACE) از خانواده توابع درهم ساز رمزنگارانه معرفی شده توسط Leuven, Belgium, Hans Dobbertin, Antoon Bosselaers و Bart Preneel در گروه پژوهشی COSIC در Katholieke Universiteit Leuven, می‌باشد، و اولین بار در سال ۱۹۹۶ منتشر شد. RIPEMD بر مبنای اصول طراحی بکار رفته در MD4 پایه‌گذاری شده بود و کارکردش مشابه SHA-1 پرطرفدار است. هرچند، RIPEMD-160 شکسته نشده‌است. RIPEMD-160 همان‌طور که از نامش پیداست، چکیده هش ۱۶۰ بیتی (۲۰ بایتی) تولید می‌کند.

Bcrypt

Bcrypt تابع درهم سازی رمزعبور است که توسط Niels Provos و David Mazières بر مبنی رمزنگار Blowfish طراحی شده‌است و در سال ۱۹۹۹ در USENIX ارائه گردید. علاوه بر یکی سازی salt برای حفاظت در برابر حملات جدول رنگین کمان، bcrypt تابع انطباقی است. با گذشت زمان، تعداد تکرار را می‌توان آهسته‌تر افزایش داد، بنابراین به حملات جستجوی فراگیر حتی با افزایش توان محاسبه مقاومت نشان می‌دهد.

Whirlpool

Whirlpool، تابع درهم ساز رمزنگارانه است که توسط Vincent Rijmen و Paulo S. L. M. Barreto طراحی شده‌است، کسانی که اولین بار در سال ۲۰۰۰ آن را توصیف کردند. Whirlpool، بر مبنای نسخه کاملاً اصلاح شده استاندارد رمزنگاری پیشرفته (AES) می‌باشد. Whirlpool چکیده درهم ۵۱۲ بیتی (۶۴ بایت) تولید می‌کند.

SHA-2

SHA-2 (الگوریتم درهم ایمن ۲) مجموعه توابع درهم رمزنگارانه می‌باشد که توسط آژانس امنیت ملی ایالات متحده (NSA) طراحی شده بود، و اولین بار در سال ۲۰۰۱ منتشر گردید. آنها با استفاده از ساختار Merkle–Damgård، از خود تابع فشرده یک سویه با استفاده از سازه Davies–Meyer از رمزنگار بلوکی تخصصی (طبقه‌بندی شده) ساخته می‌شوند.

در اصل، SHA-2 دو الگوریتم درهم دارد: SHA-256 و SHA-512. SHA-224، واریانت یا متغیره SHA-256 با مقادیر آغازین و خروجی کوتاه شده متفاوت می‌باشد. SHA-384 و SHA-512/224 و SHA-512/256 کمتر شناخته شده، همه از واریانت‌های SHA-512 بشمار می‌روند. SHA-512 امن تر از SHA-256 است و معمولاً در ماشین‌های ۶۴ بیتی مثل AMD64، سریعتر از SHA-256 می‌باشد.

اندازه خروجی بیت‌ها، با تعمیم نام "SHA" مشخص می‌شود، بنابراین SHA-224 دارای اندازه خروجی ۲۲۴ بیتی (۲۸ بایتی) است، SHA-256 32 بایت، SHA-384 48 بایت و نهایتاً SHA-512 64 بایت تولید می‌کنند.

SHA-3

SHA-3 (الگوریتم درهم ایمن ۳) در پنجم اوت ۲۰۱۵ توسط NIST معرفی شد. الگوریتم Keccak حاصل کار Guido Bertoni, Joan Daemen, Michael Peeters و Gilles Van Assche می‌باشد. Keccak بر مبنای ساخت ابر است که هم چنین قابل استفاده برای ساخت سایر ساختارهای اولیه رمزنگاری مثل رمزنگار دنباله ای است. SHA-3 اندازه خروجی مشابهی با SHA-2: 224, 256, 384 و ۵۱۲ بیتی دارد.

اندازه‌های قابل پیکربندی خروجی نیز با استفاده از توابع SHAKE-128 و SHAKE-256 بدست می‌آیند. در اینجا الحاقی‌های ۱۲۸- و ۲۵۶- دلالت ضمنی بر توان امنیتی تابع به نسبت اندازه خروجی در بیت‌ها دارند.

BLAKE2

نسخه پیشرفته BLAKE تحت نام BLAKE2 در ۲۱ دسامبر ۲۰۱۲ معرفی شد. توسط Jean-Philippe Aumasson, Samuel Neves, Zooko Wilcox-O'Hearn و Christian Winnerlein با هدف جایگزینی استفاده گسترده اما با الگوریتم‌های شکسته MD5 و SHA-1 ساخته شد. وقتی که BLAKE2b روی ساختار ARM x64 64 بیتی پیاده شود، BLAKE2b سریعتر از SHA-3, SHA-2, SHA-1 و MD5 خواهد بود. اگرچه BLAKE و BLAKE2 مثل SHA-3 استانداردسازی نشده‌اند، BLAKE2 در پروتکل‌های زیادی مثل تابع درهم رمز عبور Argon2 استفاده شد، برای راندمان بالایی که روی CPUهای پیشرفته در نظر گرفته شده‌است. وقتی که BLAKE برای SHA-3 انتخاب شد، BLAKE و BLAKE2 هر دو اندازه خروجی یکسانی مثل SHA-3 پیشنهاد دادند، که شامل اندازه خروجی قابل پیکربندی می‌شد.

BLAKE3

BLAKE3، نسخه پیشرفته BLAKE2، در ۹ ژانویه ۲۰۲۰ معرفی شد. توسط O'Connor, Jean-Philippe Aumasson, Samuel Neves و Zooko Wilcox-O'Hearn معرفی شد. BLAKE3، یک الگوریتم واحد برخلاف BLAKE و BLAKE2 است که از خانواده‌های الگوریتم‌هایی با چند واریانت می‌باشند. تابع فشرده BLAKE3 کاملاً مبتنی بر BLAKE2 می‌باشد، با بیشترین اختلاف که تعداد دور از ۱۰ به ۷ کاهش پیدا می‌کند. BLAKE3، در داخل «درخت مرکل» است و درجه‌های بالای تقارن را نسبت به BLAKE2 پشتیبانی می‌کند.

حمله روی الگوریتم‌های درهم ساز رمزنگارانه

یک فهرست طولانی از توابع درهم ساز رمزنگار است اما آسیب‌پذیری آن ثابت شده و نباید زیاد استفاده شود. برای نمونه، NIST 51 تابع درهم را به عنوان تابع منتخب برای دور ۱ رقابت هش SHA-3 انتخاب کرد، از بین آنها ۱۰ تابع شکسته و ۱۶ تابع دارای نقاط ضعف قابل توجه در نظر گرفته شدند و لذا در دور بعد شرکت داده نمی‌شدند. اطلاعات بیشتر در مورد این مبحث را می‌توان در مقاله اصلی آن در مورد "رقابت‌های تابع درهم NIST" جستجو کرد.

حتی اگر تابع درهم هرگز شکسته نشده باشد، «حمله موفق» در برابر واریانت ضعیف می‌تواند باعث تحلیل بردن اطمینان «کارشناس» شود. برای نمونه، در اوت ۲۰۰۴، برخوردها در چند تابع درهم پرطرفدار مثل MD5 مشاهده شدند (۲۰). این نقاط ضعف، امنیت الگوریتم‌های قوی تر مشتق شده از توابع درهم ضعیف خصوصاً SHA-1 (نسخه تقویت شده SHA-0)، RIPEMD-128 و RIPEMD-160 (هر دو نسخه تقویت شده RIPEMD) را زیر سؤال می‌برد.

در ۱۲ اوت ۲۰۰۴، Joux, Carribault, Lemuet و Jalby برخوردی را برای الگوریتم کامل SHA-0 معرفی کردند. Joux و همکارانش این کار را با استفاده از تعمیم دهی حمله Chabaud و Joux انجام دادند. آنها به این نتیجه رسیدند که برخورد دارای پیچیدگی 2⁵¹ بود و ۸۰۰۰۰ ساعت CPU (واحد پردازشگر مرکز) روی ابرکامپیوتری با ۲۵۶ پردازنده Itanium 2- معادل ۱۳ روز استفاده تمام وقت از ابرکامپیوتر فعال بود.

در فوریه ۲۰۰۵، حمله ای روی SHA-1 گزارش شد که در حدود عملیات درهم‌سازی ۲۶۹ را شامل می‌شد، به جای مقدار مورد انتظار ۲۸۰ برای تابع درهم ۱۶۰ بیتی. در اوت ۲۰۰۵، حمله دیگر روی SHA-1 گزارش شد که برخورد در ۲۶۳ عملیات را نشان می‌داد. نقاط ضعف نظری دیگر SHA-1 از این قرارند: (۲۱، ۲۲) و در فوریه ۲۰۱۷ گوگل خبر از برخورد در SHA-1 داد (۲۳). محققین حوزه امنیت توصیه کردند که اپلیکیشن‌های جدید می‌توانند با استفاده از اعضای خانواده SHA این مشکلات را برطرف کنند، مثل SHA-2 یا استفاده از تکنیک‌هایی نظیر درهم سازی تصادفی (۲۱)(۱) که نیازی به مقاومت در برابر برخورد ندارد.

یک حمله عملی و موفق، MD5 استفاده شده درون گواهی «امنیت لایه انتقال» را در سال ۲۰۰۸ شکست.

بسیاری از توابع درهم رمزنگار، بر مبنای "ساختار Merkle–Damgård" پایه‌گذاری شده‌اند. همه هش‌ها یا درهم رمزنگاری که مستقیماً از خروجی کامل ساختار فوق استفاده می‌کنند نسبت به حملات گسترش طول آسیب پذیرند. این باعث می‌شود تا MD5, SHA-1, RIPEMD-160, Whirlpool و الگوریتم‌های درهم SHA-256 / SHA-512، همه نسبت به این حملات ویژه آسیب‌پذیر باشند. SHA-3, BLAKE2, BLAKE3 و واریانت‌های کوتاه شده SHA-2 به این نوع حمله آسیب‌پذیر نیستند.

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Cryptographic hash function». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳ اسفند ۱۳۹۹.