نیروی لورنتس
نیروی لورنتس (Lorentz force) در فیزیک، نیروی وارد بر بار نقطهای در میدان الکترومغناطیسی است. این نیرو با استفاده از رابطهٔ زیر که شامل میدانهای الکتریکی و مغناطیسی است بیان میشود:
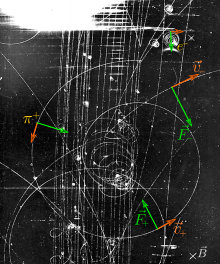
نیروی لورنتس در حالی که بر روی ذرات باردار با حرکت سریع در یک محفظه حباب اثر میگذارد. مسیر بارهای مثبت و منفی در جهت مخالف منحنی است.
که درآن
- F نیروی لورنتس برحسب نیوتون
- E میدان الکتریکی بر حسب ولتر بر متر
- B میدان مغناطیسی بر حسب تسلا
- q بار الکتریکی ماده بر حسب کولُن
- v سرعت لحظهای ذره بر حسب متر بر ثانیه.
- × علامت ضرب برداری است.
بهطور معادل عبارت زیر برای پتانسیل برداری و پتانسیل اسکالر است:
که در آن
- ∇ و ∇ × به ترتیب گرادیان و کرل هستند.
- A و ɸ پتانسیل مغناطیسی برداری و پتانسیل الکترواستاتیک میباشند که توسط فرمولهای زیر به E و B ارتباط پیدا میکنند:
این معادلات برداری هستند و کلیهٔ کمیتهایی که به صورت پررنگ نوشته شدهاند، بردار هستند. (مشخصا: F, E، v, Bو A)
قانون نیروی لورنتس رابطهٔ نزدیک با قانون القای فاراده دارد جسمی که به صورت نسبت باردار شده در همان جهت میدان الکتریکی شتاب میگیرد اما بهطور عمود بر سرعت لحظهای و میدان مغناطیسیB است و براساس قانون دست راست عمل میکند (یعنی اگر انگشت شست است راست جهت v باشد انگشت اشاره جهت B و خمش انگشتان جهت F را مشخص میکند) عبارت qE نیروی الکتریکی بیست و B× qv عبارت نیروی مغناطیسی است براساس همین رابطه نیروی لورنتس را میتوان به صورت زیر بیان کرد
با نیروی کامل الکترومغناطیسی (که شامل عبارت نیروی الکتریکی نیز هست) اسامی دیگری (که غیر استاندارد هستند) گفته میشوند که بیان نیروی لورنتس برای این نیروی کامل استانداردترین نام است. مولفهٔ مغناطیسی نیروی لورنتس نیرویی است بر سیم حامل جریان در میدان مغناطیسی دارد میشود که به تنهایی نیروی لاپلاس نامیده میشود که بزرگی این نیرو qvBsinA است و جهت آن عمود بر B,v است اگر B,v عمود باشند بزرگی این نیرو به صورت qvB خواهد بود؛ و مسیر حرکت به صورت دایرهای خواهد بود اگرچه بزرگی سرعت تغییر میکند اما جهت آن به صورت دایرهای تغییر خواهد کرد
تاریخچه[ویرایش]
اولین تلاشها برای تشریح کمّی نیروی الکترومغناطیسی در اواسط قرن ۱۸ بود که پیشنهادی بر نیروی وارد بر قطبهای مغناطیسی بود. این کار توسط جان توبیاس مایر (john tobias Mayor) و دیگران در ۱۷۶۰ و اجسام باردار الکتریکی توسط هنری کاوندیش در ۱۷۶۲ که قانون عکس مجذور فاصله پیروی میکند البته در هیچکدام از این در مورد اثباتهای تجربی کامل نشدند و تا ۱۷۸۴ تا زمانی که شارل آگوستن دو کولن با استفاده از یک تعادل پیچ خوردگی فنری توانست نشان دهد که روشهای اثبات تجربی این مسئله درست هستند. کمی بعد در ۱۸۲۰ اورستد نشان داد که عقربهٔ مغناطیسی به اعمال ولتاژ و جریان عکسالعمل نشان میدهد. در همان نسل آندره-ماری آمپر توانست رابطهٔ بین نیرو با زاویهٔ نا مشخص بین دو المان جریان را پیدا کند. در تمام این توصیفات نیرو به عنوان ویژگی خاص از یک المان در فاصلهٔ مشخص از میدان الکتریکی مغناطیسی بیان میشد. اولین بیان مدرن از مفهوم میدان الکتریکی و مغناطیسی در نظریهٔ مایکل فاراده خود را نشان داد به ویژه نظریهٔ او راجع به خطوط نیرو و بعدها توصیف ریاضی کامل این نظریه توسط لرد کلوین و جیمز کلارک ماکسول ارائه شد. ماکسول با معادلاتش راهی برای رابطهٔ بین نیروی لورنتس و میدان الکتریکی پیدا کرد. اگرچه در آن زمان کسی درک نمیکرد که الکتریسته شامل حرکت بارهای الکتریکی نیز میشود؛ و اینکه حرکت این بارهای الکتریکی باعث ایجاد میدان مغناطیسی میشود. هنری رولند در ۱۸۷۵ نشان داد که بارهای متحرک الکتریکی مانند سیم حامل جریان، میدان مغناطیسی ایجاد میکنند. در همان زمان بود که تامسون سعی میکرد با استفاده از نتایج معادلات ماکسول نیروی وارد شده (وارده) از طرف میدان مغناطیسی را بر بار الکتریکی اجسام متحرک به عنوان یک ویژگی خارجی اثبات کند. در توجیه رفتار الکترومغناطیسی در پرتوهای کاتدی تامسون مقالهای در ۱۸۸۱ چاپ کرد و در آن نیروی وارد بر بار از طرف میدان خارجی را با رابطهٔ زیر به دست آورد.[۱]
تامسون به یک فرمول درست رسید. اما به دلیل برخی اشتباهات در محاسبه و توصیف نادرست جریان جابهجایی یکای اشتباهی برای فرمول به دست آورد. الیور هِویساید تعریف جدیدی از بردار ارائه داد و از آنها در معادلات ماکسول استفاده کرد و در نسلهای ۱۸۸۵ و ۱۸۸۹ رابط تامسون را تصحیح کرد و به شکل درست معادلات رسید و نهایتاً در ۱۸۹۲ هنریک لورنتس توانست رابطهٔ کلی نیرو را که هم شامل میدان الکتریکی و هم شامل میدان مغناطیسی بود بیاید. لورنتس معادلات ماکسول در رابطه بالاتر و رسانایی صرف نظر کرد و در عوض میان ماده واتر شفاف قائل شد و توانست معادلات ماکسول را در مقیاس میکروسکوپیک بیان کند. با استفاده از مدل هویساید از معادلات ماکسول برای اتر ساکن و استفاده از مکانیک لاگرانژی لورنتس به نرم صحیح و کامل نیرو رسید و نام خود را ثبت کرد.
اهمیت نیروی لورنتس[ویرایش]
در حالی که معادلات مدرن ماکسول نشان میدهند که چگونه بار و اجسام باردار در مقابل میدانهای مغناطیسی و الکتریکی رفتار میکنند. قانون نیروی لورنتس این تصویر ذهنی را بر بار این بیان که بار متحرک q در مقابل میدان مغناطیسی قرار دارد، تکمیل میکند. قانون نیروی لورنتس اثرات میدانهای B,E را بر یک بار نقطهای بیان میکند اما همانند نیروهای الکترومغناطیسی همهٔ تصویر را نشان نمیدهد بارها اغلب به نیروهای دیگری تبدیل میشوند بهطور برجسته، جاذبه و نیروی هستهای بنابراین معادلات ماکسول جدا از سایر قوانین فیزیک قرار نمیگیرد اما با آنها با بار و چگالی جریان پیوند میخورد. واکنش یک ذره به باردار به نیروی لورنتس یک جنبه و تولید B,E توسط جریان و بار جنبهٔ دیگر قضیه است. در مواد واقعی نیروی لورنتس برای توصیف رفتار بار کافی نیست نه در توصیف نیروها و نه حتی در محاسبه. قسمتهای باردار در ماده بهطور متوسط به B,E واکنش نشان میدهند و حتی آنها را تولید نیز میکنند. معادلات پیچیدهتر باید زمان و فاصلهٔ بین بارها را نیز محاسبه کنند، مانند معادلات بولتزمن یا معادلات فوکر، پلانک یا معادلات ناویِر استوکس. همچنین مغناطیس شارهها دینامیک سیادلات و همچنین تحولات ستارهای که کل فیزیک به علت سر و کار داشتن با این مفاهیم تغییر کردهاست. اگر چه ممکن است عدهای این تئوریها را ترتیبی برای واقعیت یا اجسام بزرگ بدانند اما با یک نگاه عمیقتر میتوان به این نکته پی برد که بررسی ذرات باعث به وجود آمدن نیروهایی جاذبه یا نیروی هستهای یا به وجود آمدن شرایط مرزی میشود و این مختص الکترومغناطیس نیست بلکه شامل تمام قسمتها میشود.
نیروی لورنتس توصیفی برای B,E[ویرایش]
در بسیاری از کتابهای درسی در الکترومغناطیس کلاسیک نیروی لورنتس راهی برای توصیف میدانهای B,E است برای مثال نیروی لورنتس به صورت زیر بیان میشود. نیروی الکترومغناطیسی وارد بر بار آزمون به صورت تابعی از بار و سرعت بیان میشود که با پارامتری کردن توسط دو بردار B,E به صورت زیر بیان میشود:
اگر فرض کنیم که این بیان تجربی صحیح باشد (که تعداد بی شماری از آزمایشها ثابت کردهاند که صحیح است) دو میدان برداری E,B وجود دارند که فضا و زمان را پر کردهاند که میدان الکتریک و میدان مغناطیسی نامیده میشوند. باید توجه کرد که میدانها هر جایی در فضا و زمان مطرح میشوند بدون توجه به اینکه آیا به ذره نیرویی دارد میشود یا نه بهطور مشخص میدانها نسبت به نیرویی که بار آزمون فرضی متوجه ان است قرار میگیرند. توجه کنید که به عنوان توصیفی از B,E نیروی لورنتس تنها یک بیان قابل استنباط است. معکوس ان نیز قابل استفاده است یعنی از معادلات ماکسول و نیروی لورنتس میتوان به قانون فاراده رسید.
نیروی لورنتس و قانون القای فاراده[ویرایش]
با استفاده از قانون القای فاراده برای یک حلقه سیم در میدان مغناطیسی داریم:
که در آن:
- شار مغناطیسی
- نیروی الکتروموتوری
هستند
که این قانون هم برای سیم ساکن هم سیم متحرک صادق است.
فرض میکنیم یک سیستم حامل جریان باشد که بدون چرخش دارای سرعت ثابت v است و سطح کل سیم است مقدار emf در یک سطح بسته توسط رابطهای زیر داده میشود.
که dℓ المانی از سطح منحنی است. شار ΦB در قانون فاراده بهطور واضح از رابطه زیر به دست میآید.
که در آن: سطحی است که توسط محسور شدهاست. E میدان الکتریکی dℓ یک المان بسیار کوچک از سطح ، V سرعت المان بسیار کوچک B میدان مغناطیسی
برای هر دو بردار dℓ و dA یک ابهام وجود دارد که برای تعیین علامت صحیح از قانون دست راست و قانون استوکس استفاده میشود تمام نتایج بالا در قانون القای فاراده بیان میشود که نتیجهٔ آن صورت جدیدی از معادلات ماکسول است که رابطهٔ ماکسول فاراده خوانده میشود.
که این رابطه با استفاده از قانون استوکس به شکل انتگرالی زیر است بدست میآید.
و قانون فاراده:
که با استفاده از رابطهٔ لایبنیتس به صورت ریز در میآید:
و در نهایت رابطه ماکسول-فاراده:
که این برای سیم ساکن و متحرک صادق است:
قانون القای فاراده هم برای سیم صلب ساکن و هم برای اجسام متحرک کاربرد با حضور میدان مغناطیسی متغیر با زمان یا ثابت کاربرد دارد. البته موارد ی وجود دارند که قانون فاراده برای آنها قابل استفاده نیست یا بسیار دشوار است که با آنها تطابق پیدا کند و است تضمینی برای ضرورت وجود نیروی لورنتس است. اگر میدان مغناطیسی با زمان تغییر نکند و حلقه رسانا در میدان حرکت کند شار مغناطیسی حلقه به طرق مختلف تغییر میکند. برای مثال اگر جهت میدان Bتغییر کند تغییر شار حلقهٔ مخالف جهت حرکت B است. به همین ترتیب اگر جهت حلقه نسبت به میدان B تغییر کند المان دیفرانسیلی B•dA نیز تغییر خواهد کرد. به دلیل اینکه زاویهٔ بین dA و B تغییر میکند بنابراین شار نیز تغییر میکند. در حالت سوم نیز اگر زاویهٔ حلقه تغییر کند شار با حرکت آن مجدداً مخالفت خواهد کرد.
در تمامی این حالتها قانون فاراده وجود نیروی emf را به دلیل وجود شار ΦB. پیش گویی میکند توجه کنید که عبارت ماکسول، فاراده ایجاب میکند که در صورت تغییر میدان B با زمان، E بدون تغییر باقی بماند.
قانون لورنتس بر حسب پتانسیل[ویرایش]
اگر پتانسیلهای اسکالر و برداری را جایگزین B,E کنیم نیروی لورنتس به فرم زیر در میآید.
یا بهطور معادل (با توجه به اینکه v ثابت است)
که در آن A پتانسیل برداری مغناطیسی
- پتانسیل الکتروستاتیکی است؛ و نمادهای ، نمایشگر، گرادیان، کرل و دیورژانس هستند. پتانسیل با B,E از طریق رابطهٔ زیر مربوط میشود.
نیروی لورنتس در دستگاه cgs[ویرایش]
در فرمولی که در بالا ذکر شد از B دستگاه SI استفاده شد که در بین مهندسان و دانشمندان بسیار رایج است. دستگاه cgs در بین فیزیکدانان نظری بسیار رایج است. یکی از تفاوتهای آن:
که در آن c سرعت نور است. اگر چه این عبارت کاملاً متفاوت از معادل ان به نظر میرسد روابط زیر را نیز میتوان خاطر نشان شد:
، ، and
که در آن ε۰ و μ۰ ضریب گذر دهی الکتریکی و مغناطیسی در خلاء هستند در عمل متأسفانه ذکر نمیشود که دستگاه مورد استفاده SIاست یا cgs و این مطلب باید از متن نوشته درک شود.
شکل چند متغیری نیروی لورنتس[ویرایش]
قانون حرکت نیوتن در شکل چند متغیری براساس تنسور نیروی مغناطیسی به صورت زیر بیان میشود.
که در آن t زمان، q بار و u چهار بردار سرعت است که از رابطه زیر به دست میآید.
با استفاده از توصیف بالا برای نیروی لورنتس تنسور نیروی الکترو مغناطیسی به صورت زیر در میآید:
- .
میدان توسط قاب متحرکی که با سرعت نسبی ثابت حرکت میکند جابهجا میشود و این سرعت از رابطهٔ زیر به دست میآید:
که در آن جا به جایی لورنتس است. بهطور مشابه با استفاده از چهار بردار:
که به میدانهای الکتریکی و مغناطیسی با رابطهٔ زیر مربوط میشود.
تنسور میدان به شکل:
در میآید که در آن
نماد سازی برداری[ویرایش]
برای مؤلفهٔ x نیرو میتوان نوشت:
که در آن t زمان مشخصهاست جاگذاری این مؤلفه در تنسور نیروی الکترومغناطیسی منتج به این نتیجه میشود.
با نوشتن چهار برداری سرعت
برای سایر مؤلفهها نیز به همین ترتیب داریم.
و به بیان پتانسیل برداری و اسکالر A و φ:
نیرو وارد بر سیم حامل جریان[ویرایش]
هنگامی که یک سیم حامل جریان در یک میدان مغناطیسی قرار بگیرد هر کدام از بارهای متحرک که عامل ایجاد جریان هستند نیروی لورنتس برآنها وارد میشود و در مقیاس ماکروسکوپی میتوانند بر سیم حامل جریان نیرو وارد کنند. (گاهی نیروی لاپلاس نامیده میشود). با ترکیب نیروی لورنتس با تعاریف نیروی الکتریکی عبارت زیر برای یک سیم ثابت و صاف حامل جریان بدست میآید:
بهطور معادل میتوان رابطهٔ زیر را نیز نوشت
که در آن جهت بردار با جهت جریان متغیر، تغییر میکند و هر دو فرم بالا با هم معادل هستند (این یک نیروی خالص است به علاوه در صورت صلب نبودن سیم گاهی ممکن است نیروی گشتاور نیز ایجاد شود).
EMF[ویرایش]
نیروی مغناطیسی (q v × B) میتواند به عنوان نیروی جنبشی الکتروموتوری (emf) در نظر گرفته شود که این پدیده در بسیاری از ژنراتورها اتفاق میافتد وقتی یک مادهٔ رسانا در میدان مغناطیسی حرکت میکند. نیروی مغناطیسی بر الکترونهای سیم نیرو دار میکند و این باعث به وجود آمدن emf میشود و emf باعث حرکت سیم میشود. در سایر ژنراتورها در حالی که رسانا ساکن است آهنربا حرکت داده میشود در این حالت emf باعث ایجاد نیروی الکتریکی qE میشود در این حالت نیروی الکتریکی به دلیل میدان مغناطیسی متحرک ایجاد میشود و این نیروی emf القایی را ایجاد میکند که توسط رابطه ماکسول فاراده توصیف میشود. هر دو این emfها با این که منشاء متفاوت دارند با یک رابطه که شار مغناطیسی وارد بر سیم نامیده میشود محاسبه میشوند (قانون القای فاراده) نسبیت خاص اینشتین تا حدودی باعث درک بهتر این پدیده شد. در واقع نیروهای الکتریکی و مغناطیسی دو روی نیروی واحد الکترومغناطیس هستند.
منابع[ویرایش]
- ↑ https://books.google.co.uk/books?id=e9wEntQmA0IC&pg=PA120&redir_esc=y&hl=en#v=onepage&q&f=false Oliver Heaviside By Paul J. Nahin, p120
| در ویکیانبار پروندههایی دربارهٔ نیروی لورنتس موجود است. |
- مقالهٔ ویکیپدیای انگلیسی: http://en.wikipedia.org/wiki/Lorentz_force








![{\displaystyle \mathbf {F} =q[\mathbf {E} +(\mathbf {v} \times \mathbf {B} )].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc7d5dc02e627206cc39da6a4b66ff13c3393d17)







































