میدان برداری

نمودار میدان برداری

$f(x,y)=(-y,x)$

میدان برداری، در ریاضیات، تابعی است که به هر نقطه از فضای اقلیدسی برداری را نسبت می‌دهد.

.نمومه ای از این میدان در طبیعت میدان گرانشی و مغناطیسی است. ودر فیزیک، مثلا برای مدل‌سازی راستای حرکت و سرعت ذرات شاره‌ها، بکار می‌رود. اگر میدان برداری نشاندهنده ی نیرو در فضا باشد با انتگرال گیری خطی در واقع میزان کار را بدست می آوریم. یکی از مهمترین کاربرد میدان برداری نشان دادن سرعت یک سیال جاری در فضا است و سپس با توجه به مفاهیمی چون دیورژانس و کرل و ... به بررسی جریان می پردازیم. یک میدان برداری بر (R^n) نگاشتی چون (F: R^n -> R^n) است که به هر نقطه‌ی (x) در قلمری (A)ایه آن فضای برداری را نسبت می‌‌دهد.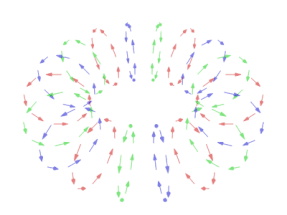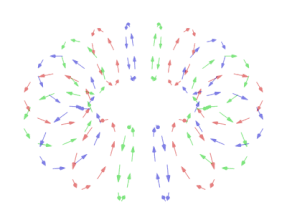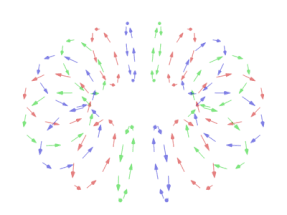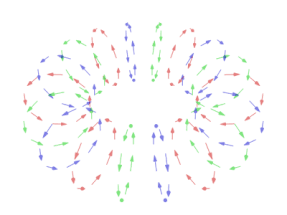 در واقع می‌توان گفت میدان برداری F به هر نقطه که در دامنهٔ خودش یک بردار نسبت می‌‌دهد

اگر روی این بردار حرکت کنیم،پایان بردار نقطه‌ را نشان می‌‌دهد که می‌توان گفت میدان برداری هر نقطه از قلمری خودش را به نقطه‌ای نسبت می‌‌دهد.در این حالت خاص میدان میدان اسکلری می‌خوانیم. فرم کلی‌ بردار‌های برداری به سرعت (طبیعی برداری) است.همانطور که گفتیم میدان‌های برداری به هر نقطه یک بردار نسبت داده،در اینجا به نقطه‌ی (x) بردار F1(x,y,z)به نقطه‌ی ((y بردار F2(x,y,z) و به نقطه‌ی (z) بردار F3(x,y,z) را نسبت داده اند.

کرل میدان برداری

کرل یا تاو یک میدان برداری بردریست که اندازهٔ آن نشانگر حداکثر گردش آن بردار در واحده سطح است.

یک میدان برداری که کرل نداشته باشد میدان برداری غیر گردشی یا ذخیره شونده نامید میشود.

اگر میدان برداری به صورت (V(x,y,z)=(Vx,Vy,Vzباشد کرل آن میدان به صورت زیر است

(کرل میدان‌های برداری از ضرب خارجی‌ برداری عملگر دل‌ در بردار میدانی مورد نظر به دست می‌آید.)

$\mbox{curl}\;\vec v = \left( {\partial v_z \over \partial y} - {\partial v_y \over \partial z} \right) \mathbf{i} + \left( {\partial v_x \over \partial z} - {\partial v_z \over \partial x} \right) \mathbf{j} + \left( {\partial v_y \over \partial x} - {\partial v_x \over \partial y} \right) \mathbf{k} = \nabla \times \vec v$

که معادل است با دترمینان ماتریسی که

$\nabla \times \vec v = \left|\begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \\ {\frac{\partial}{\partial x}} & {\frac{\partial}{\partial y}} & {\frac{\partial}{\partial z}} \\ \\ v_x & v_y & v_z \end{matrix}\right|.$

اگر میدان برداری (F‌) شارش یک سیال را نشان دهد، هنگام شارش میدان برداری مذکور،گردشی در کار نیست اگر و فقط اگر

    Curl(F)=0

دیورژانس یک میدان برداری

دیورژانس یک میدان برداری به صورت ضرب داخلی‌ عملگر دل‌ در میدان برداری بدست می‌آید.

$\operatorname{div}\,\mathbf{F} = \nabla\cdot\mathbf{F} =\frac{\partial F_x}{\partial x} +\frac{\partial F_y}{\partial y} +\frac{\partial F_z}{\partial z}.$

دیورژانس یک اپراتور برداری است که میزان "شار خروجی" یا "جذب از محیط" یک میدان برداری را در یک نقطه بوسیله یک اسکالر علامت دار اندازه گیری می کند.

به عبارت تخصصی‌تر، دیورژانس نشان‌دهنده چگالی حجمی شار خروجی از (یا ورودی به) یک حجم بسیار کوچک می باشد.

می‌توان گفت مقدار دیورژانس میزان انبساط در واحد حجم مایعی یا گاز را نشان می‌‌دهد.

در ویکی‌انبار پرونده‌هایی دربارهٔ میدان برداری موجود است.

انتگرال میدان برداری در امتداد خم

فرض کنید L:[a,b]→R^n یک خم هموار باشد.نماد ( r=L(tرا اکثرا استفاده می‌کنیم و می‌دانیم dr/ds = T مماس واحد خم L در جهت حرکت است.T تحت اثر باز پرمایش جهت نگهدار تغییر نمیکند ولی‌ اگر پارامتر ساز جهت برگردان باشد،T به T- تبدیل میشود.فرض کنید Fمیدان برداری پیوسته باشد که دامنه تعریفش شامل تصویر Lاست.اینگونه تعریف می‌کنیم:
ʃF.dr=ʃ(F.T)ds
توجه کنید که اگر یک پارامترساز جهت برگردان صورت گیرد، Tدر -۱ ضرب میشود،در نتیجه انتگرال بالا وابسته به جهت است.