برگشت به میانگین

شرایط آزمایش گالتون (شکل ۸)

در علم آمار، برگشت به میانگین (که واژهٔ برگشت از عبارت Regression ترجمه شده‌است) به پدیده‌ای گفته می‌شود که اگر یک نمونه از متغیری تصادفی، مقداری حدی داشته باشد، نمونه‌گیری بعدی از همان متغیر تصادفی احتمالاً به میانگین نزدیک‌تر است. علاوه بر این، زمانی که تعداد زیادی نمونه‌گیری از متغیر تصادفی خاصی انجام و حدی‌ترین نمونه‌ها عمداً جدا شده باشند، (در بسیاری از موارد) نمونه‌گیریِ دوباره از این متغییرهای تفکیک شده منجر به نتایجی می‌شود که به میانگین اولیه تمامی متغییرها نزدیک‌ترند و نتایج حدی کمتری دارند.

از نظر ریاضی، شدت «برگشت» به این بستگی دارد که همهٔ متغیرهای تصادفی از یک توزیع برداشت شده باشند یا توزیع هر یک از متغییرهای تصادفی تفاوت‌های اساسی واقعی داشته باشد. در حالت اول، اثر «برگشت» از نظر آماری احتمال وقوع دارد، اما در مورد دوم، ممکن است احتمالی بسیار کمتر داشته باشد یا اصلاً رخ ندهد.

بنابراین، لحاظ پدیدهٔ برگشت به میانگین برای طراحی هر آزمایش علمی، تحلیل داده یا آزمونی که در آن به عمد «حدی‌ترین» رویدادها انتخاب می‌شوند مفید است. بر این اساس برای اجتناب از جمع‌بندی‌های شتاب زده در مورد این رویدادها شاید بررسی‌های بیشتری لازم باشد چرا که ممکن است این نمونه‌ها در واقع رویدادهایی حدی باشند یا به دلیل پارازیت آماری، گزینشی کاملاً بی‌معنی انجام شده یا ترکیبی از این دو حالت صادق باشد.

مثال‌های مفهومی

مثال ساده: آزمون دانش‌آموزان

دانش آموزان کلاسی را در نظر بگیرید که در آزمونی با ۱۰۰ سؤال دو گزینه‌ای صحیح/غلط شرکت می‌کنند. با فرض اینکه همه دانش‌آموزان تصادفی پاسخ سؤال‌ها را انتخاب کنند، نمرهٔ هر دانش آموز مصداق حالت خاصی از [کل حالات ممکن] مجموعهٔ متغیرهای تصادفی مستقل با توزیع یکسان، و میانگین مورد انتظار ۵۰ خواهد بود. طبیعی است که نمرهٔ برخی از دانش‌آموزان به طور شانسی تا حد قابل توجهی بیشتر از ۵۰ و نمرهٔ برخی دیگر به طور قابل ملاحظه‌ای کمتر از ۵۰ باشد. اگر فردی ۱۰ درصد از دانش‌آموزانی را که بیشترین امتیاز را کسب کرده‌اند انتخاب و آزمون دیگری برگزار کند که در آن آزمون دانش آموزان منتخب دوباره به‌طور تصادفی به همهٔ سؤال‌ها پاسخ دهند، انتظار می‌رود میانگین نمره‌های کسب شده جدید باز نزدیک به ۵۰ باشد؛ بنابراین، میانگین این دانش‌آموزان بار دیگر به میانگین تمام دانش‌آموزانی که در آزمون اصلی شرکت کرده بودند «برمی‌گردد». مهم نیست که هر دانش آموز در آزمون اصلی چه نمره‌ای گرفته باشد، بهترین پیش‌بینی نمرهٔ هر دانش آموز در آزمون دوم، ۵۰ است.

اگر انتخاب پاسخ‌های آزمون تصادفی نبود (یعنی اگر در پاسخ‌های دانش آموزان شانس (خوب یا بد) یا حدس تصادفی دخیل نبود) از همه دانش‌آموزان انتظار می‌رفت که در آزمون دوم همان امتیاز آزمون اول را کسب کنند و هیچ برگشت به میانگینی وجود نداشت.

وضعیت‌های واقعی اغلب چیزی بین این دو حالت حدی هستند: برای مثال، ممکن است نمرات امتحان را ترکیبی از مهارت و شانس در نظر بگیریم. در این صورت، زیرمجموعه دانش‌آموزانی که امتیازی بالاتر از میانگین را کسب کرده‌اند، شامل افرادی می‌شود که ماهر بوده‌اند و بدشانسی خاصی نداشته‌اند، و نیز کسانی که مهارتی نداشتند، اما بسیار خوش شانس بودند. پس از برگزاری آزمون مجدد برای این زیر مجموعه، بعید به نظر می‌رسند که افراد فاقد مهارت مجدداً شانس بیاورند، در حالی که به افراد ماهر شانس دومی داده می‌شود که بدشانسی بیاورند. از این رو، بعید به نظر می‌رسند کسانی که قبلاً خوب بوده‌اند در آزمون دوم دقیقاً به خوبی آزمود اول عمل کنند.

مثال بعد نمونهٔ دیگری از برگشت به میانگین است. دانش‌آموزان کلاسی در دو روز متوالی به دو سری سؤال متفاوت از یک آزمون پاسخ می‌دهند. اغلب مشاهده شده‌است که دانش‌آموزانی که در روز اول بدترین نمرات را آورده‌اند در روز دوم نمرات بهتری کسب کرده‌اند و دانش‌آموزانی که در روز اول بهترین نمرات را کسب کرده‌اند نسبتاً بدتر شده‌است. علت این پدیده آن است که نمرات دانش‌آموز تا حدی تابع توانایی‌های واقعی آن‌ها است و تا حدودی تابع تصادف است. در آزمون اول، برخی خوش‌شانس خواهند بود و نسبت به توانایی خود نمرهٔ بهتری کسب خواهند کرد و برخی بدشانس خواهند بود و نمره کمتری از توانایی خود کسب خواهند کرد. برخی از دانش آموزان خوش‌شانس آزمون اول در آزمون دوم هم دوباره شانس خواهند آورد، اما تعداد آن‌هایی که نمراتشان برابر معدل ([توانایی] خود) یا کمتر از معدلشان است بیشتر خواهد بود؛ بنابراین برای دانش‌آموزی که در آزمون اول خوش شانس بوده و نمره‌ای فراتر از توانایی خود به دست آورده‌اند، احتمال اینکه در آزمون دوم نمره بدتری به دست بیاورند بیشتر است. به همین ترتیب، دانش آموزانی که در آزمون اول با بدشانسی نسبت به توانایی خود نمرهٔ کمتری گرفته‌اند، به احتمال زیاد شاهد افزایش نمرات خود در آزمون دوم خواهند بود. هر قدر تأثیر شانس در خلق رویدادهای حدی بیشتر باشد، احتمال این که شانس در چندین رویداد تکرار شود کمتر است.

مثال‌های دیگر

اگر تیم ورزشی محبوب شما در سال قبل جام قهرمانی را برنده شده باشد، از این رویداد برای احتمال بردن جام فصل بعد چه برداشتی می‌توان داشت؟ هر قدر که این نتیجه به دلیل مهارت تیم باشد (تیم در شرایط خوبی باشد، بهترین مربی‌ها را داشته باشد و …) برد نشانه‌ای است از این که احتمال پیروزی آن‌ها در سال آینده بیشتر است. اما هر قدر دستاورد فصل گذشته بیشتر شانسی بوده باشد (تیم‌های دیگر درگیر رسوایی مواد مخدر بوده‌اند، قرعه کشی به نفع تیم تمام شده، قرعه کشی جذب بازیکنان مؤثر بوده و غیره)، احتمال بردن جام در سال آینده کمتر است.

اگر بنگاهی اقتصادی فصل بسیار سودآوری را پشت سر گذاشته باشد، در حالی که دلایل اساسی عملکرد آن نسبت به فصل قبل تغییر نکرده‌است، احتمالاً در سه‌ماهه بعدی عملکرد ضعیف‌تری خواهد داشت.

بازیکنان بیسبال تازه‌کار که در اولین فصل بازی خود عملکرد خوبی نشان می‌دهند، احتمالاً در فصل بعد بدتر خواهند بود چیزی که «پسرفت سال دومی‌ها» نامیده می‌شود. برگشت به میانگین باور عمومی به نفرین جَرایِد را نیز به همان شکل تبیین می‌کند (اینکه پس از عملکرد استثنایی ورزشکار تصویر او در جلد مجلات چاپ می‌شود و پس از آن احتمال عملکرد معمولی ورزشکار در دوره‌های بعد بیشتر می‌شود گویی ظاهر شدن ورزشکار در جلد مجلات باعث افت وی شده‌است).

تاریخچه

کشف

نمواری که فرانسیس گالتون در سال ۱۸۸۶ برای نشان دادن ارتباط بین قد بزرگسالان و والدین آن‌ها ترسیم کرد. مشاهده حاکی از آن بود که قد کودکان در بزرگسالی انحراف کمتری از میانگین دارند تا قد والدینشان و مفهوم «برگشت به میانگین» را پیشنهاد کرد. نام تحلیل رگرسیون از این‌جا آمده‌است.

مفهوم رگرسیون از ژنتیک سرچشمه می‌گیرد و با انتشار اثر سر فرانسیس گالتون در اواخر قرن نوزدهم با عنوان برگشت به میانگین در وراثت قد شهرت گرفت. گالتون مشاهده کرد که ویژگی‌هایی حدی (مانند قد) در والدین به طور کامل به فرزندان آن‌ها منتقل نمی‌شود. در عوض، این ویژگی‌ها در فرزندان به سمت یک نقطه متوسط عقب می‌نشینند (نقطه‌ای که پس از آن میانگین نامیده شد). او توانست با اندازه‌گیری قد صدها نفر، این برگشت به میانگین را کمّی کند و اندازه این تأثیر را تخمین بزند. بر اساس نوشته‌های گالتون «برگشت متوسط فرزندان کسر ثابتی از انحرافات میانگین موزون قد والدین آن‌ها است». یعنی تفاوت یکی از ویژگی‌های فرزند و والدینش با میزان اختلاف آن ویژگی در والدین با افراد معمولی آن جامعهٔ آماری ([میانگین جامعه]) متناسب است. اگر قد هر یک از والدین فرد دو اینچ از میانگین قد مردان و زنان بلندتر باشد، در این صورت، فرزند این زوج به طور متوسط، معادل عدد ثابتی (که اکنون آن را یک منهای ضریب رگرسیون می‌نامیم) ضرب در دو اینچ، کوتاهتر از والدین خود خواهد بود. گالتون این ضریب را برای قد حدود ۲/۳ تخمین زد: قد فرد اطراف نقطه‌ای بینابینی قرار خواهد گرفت که دو سوم انحراف والدین از میانگین جامعهٔ آماری است.

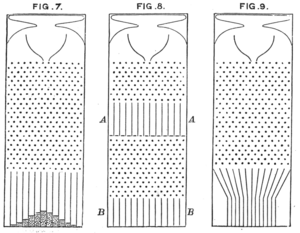
گالتون با استفاده از مثالی ساده‌تر نیز این نتایج را منتشر کرد. وی در این مثال از گلوله‌هایی استفاده کرد از داخل تختهٔ گالتون به پایین سرازیر می‌شدند و توزیع نرمالی شکل می‌دادند که مرکز آن مستقیماً زیر نقطهٔ ورودی گلوله‌ها قرار داشت. می‌شد این گلوله‌ها را دوباره از طریق مجرای دیگری به پایین هدایت کرد که به نقطهٔ سنجشی ثانوی مرتبط بود. سپس گالتون سؤال را وارونه کرد: «این گلوله‌ها از کجا آمده‌اند؟»

«به‌طور متوسط مستقیماً از بالا» پاسخ این سؤال نیست. پاسخ صحیح این است: «به‌طور متوسط، بیشتر از وسط»، به این دلیل ساده که در میانهٔ تخته گلوله‌های بیشتری وجود دارند و احتمال اینکه گلوله‌ها از میانه به پایین سرازیر شده و برخی به کناره‌ها منحرف شده باشند بیشتر از آن است که از منتهی الیه کناره‌ها به پایین سرازیر شده و برخی به میانه‌ها منحرف شده باشند.

کاربرد تکامل یافتهٔ این اصطلاح

گالتون اصطلاح «رگرسیون» را برای توصیف واقعیتی قابل مشاهده در وراثتِ صفات ژنتیکیِ کمی چند عاملی ابداع کرد: یعنی صفات فرزندانِ والدینی که در انتهای توزیع قرار می‌گیرند اغلب به مرکز یا میانگین توزیع گرایش بیشتری دارند. او این روند را کمّی و به ا ین منظور تحلیل رگرسیون خطی را اختراع کرد، به این صورت زمینه برای موارد بسیاری از مدل‌سازی‌های آماری مدرن فراهم شد. از آن زمان، اصطلاح «رگرسیون» در زمینه‌های دیگری استفاده شده‌است، و دانشمندان علوم آمار مدرن می‌توانند از آن برای توصیف پدیده‌هایی مانند سوگیری نمونه‌گیری استفاده کنند که ارتباط چندانی با مشاهدات اصلی گالتون در زمینه ژنتیک ندارد.

گالتون پدیدهٔ رگرسیون را که در زیست‌شناسی مشاهده کرد چنین شرح داده‌است: «کودک [ویژگی‌های خود را] تا حدی از والدین و میزانی از اجدادش ارث می‌برد. به طور کلی، هرچه در تبارشناسی کودک عقب‌تر رویم، اجداد او متعددتر و متنوع تر می‌شوند، تا زمانی که دیگر با نمونه‌های تصادفی با همان تعداد از کل آن نژاد تفاوتی نخواهد داشت.» نیاز است گفتهٔ گالتون با استفاده از دانش ژنتیک، کمی توضیحی داده شود: کودکان موارد ژنتیکی را از والدین خود دریافت می‌کنند، اما اطلاعات وراثتی (مثلاً مقادیر صفات به ارث برده شده) ممکن است به واسطهٔ والدینشان از اجداد قبلی به آنها منتقل شود (و ممکن است در والدین آنها بیان نشده باشد). شاید میانگین صفت وراثتی غیرتصادفی باشد و با فشار انتخاب تعیین شود، اما پراکندگی مقادیر حول میانگین، توزیع آماری نرمال را تصویر می‌کند.

پدیده ژنتیک جمعیت که توسط گالتون مطالعه شد، مورد خاصی از «برگشت به میانگین» است. این اصطلاح اغلب برای توصیف بسیاری از پدیده‌های آماری استفاده می‌شود که داده‌ها حول میانگینی مشخص توزیعی نرمال دارند.

اهمیت

برگشت به میانگین مسئلهٔ مهمی است که در طراحی آزمایش‌ها مورد توجه قرار می‌گیرد.

برای مثال ۱۰۰۰ نفر هم سن را در نظر بگیرید که خطر ابتلا به حمله قلبی در آن‌ها معاینه شده‌است و بر این اساس امتیاز گرفته‌اند. می‌توان با استفاده از علم آمار آزمونی طراحی کرد که با درجه‌ای از عدم قطعیت تأثیر مداخلهٔ درمانی را در ۵۰ نفر از افرادی که در معرض بیشترین خطر قرار داشتند بسنجد. مداخله ممکن است هر نوع تغییر رژیم غذایی، ورزش یا درمان دارویی باشد. حتی اگر مداخلات بی‌اثر باشند باز به دلیل پدیدهٔ برگشت به میانگین انتظار می‌رود که در معاینه پزشکی بعدیِ گروه آزمایش، بهبود مشاهده شود. بهترین راه برای مبارزه با این اثر تقسیم تصادفی گروه آزمایش به یک گروه درمانی است که درمان را دریافت می‌کند و گروهی که درمان دریافت نمی‌کند. درمان تنها در صورتی مؤثر ارزیابی می‌شود که گروه درمان شده نسبت به گروه درمان نشده بهبود بشتری داشته باشند.

از طرف دیگر، می‌توان با هدف شناسایی افرادی با پتانسیل تحصیلی بالاتر، گروهی از کودکان کم‌بضاعت را آزمود. سپس برای ۱٪ برتر آزمون، دوره‌های ویژهٔ پیشرفته، تدریس خصوصی، مشاوره و رایانه فراهم کرد. حتی اگر این برنامه مؤثر باشد شاید یک سال دیگر با تکرار آزمون میانگین نمرات آن‌ها کمتر شود. با این حال، شاید در این شرایط در نظر گفتن گروه کنترلی متشکل از کودکان کم‌بضاعت که نیازهای ویژهٔ آن‌ها نادیده گرفته شده‌است غیراخلاقی تلقی شود. ممکن است محاسبات ریاضی انقباضی این اثر را تعدیل کند، اگرچه به اندازه روش گروه کنترل قابل اتکا نخواهد بود (همچنین مراجعه شود به مثال استاین).

همچنین این اثر در استنتاج آماری و تخمین کاربرد دارد. احتمال اینکه گرم‌ترین مکان کشور در روز گذشته، فردا خنک تر شود بیشتر از آن است که گرم تر شود. صندوق سرمایه‌گذاری مشترکی که در طول سه سال گذشته بهترین عملکرد را داشته‌است در سه سال آینده با احتمال بیشتری شاهد کاهش عملکرد نسبی خواهد شد تا بهبود عملکرد. احتمال اینکه موفق‌ترین بازیگر هالیوود امسال در فصل بعدی خود سود کمتری به دست‌آورد بیشتر است تا احتمال اینکه سود بیشتری به دست‌آورد. بازیکن بیسبالی که بالاترین میانگین ضربه زدن را در مسابقات آل استار را داشته‌است، به احتمال بیشتر در نیم فصل دوم میانگین پایین‌تری خواهد داشت تا اینکه میانگین بالاتری به دست بیاورد.

سوء برداشت‌ها

ممکن است مفهوم برگشت به میانگین به اشتباه استفاده شود.

در مثال آزمون دانش‌آموزان قبلی، به طور ضمنی فرض شده بود که آنچه اندازه‌گیری می‌شود در فاصلهٔ دو اندازه‌گیری تغییر نمی‌کند. با این حال، فرض کنید که نتیجهٔ دوره دو حالت قبولی یا مردودی داشته باشد و دانش آموزان برای قبولی باید در هر دو آزمون نمره‌ای بالاتر از ۷۰ کسب کنند. پس دانش‌آموزانی که نمرهٔ اولشان کمتر از ۷۰ باشد انگیزه‌ای برای عملکرد خوب نخواهند داشت و ممکن است بار دوم به‌طور میانگین نمره بدتری کسب کنند. از سوی دیگر، دانش آموزانی که نمرهٔ بالای ۷۰ کسب کنند برای مطالعه قبل از آزمون و تمرکز حین آزمون انگیزه‌ای قوی خواهند داشت. در این صورت ممکن است مشاهده شود که نمره‌ها از ۷۰ فاصله می‌گیرند به این صورت که نمره‌های کمتر از ۷۰ باز هم کمتر می‌شوند و نمره‌های بالای ۷۰ بیشتر. ممکن است، تغییرات بین زمان‌های اندازه‌گیری باعث تقویت، خنثی یا معکوس کردن گرایش آماری برای برگشت به میانگین شود.

برگشت آماری به میانگین پدیده‌ای علّی نیست. دانش آموزی که در روز اول بدترین نمره را در آزمون داشته باشد، لزوماً به دلیل این پدیده، نمرهٔ خود را در روز دوم بهبود نخواهد داد. به طور میانگین [در آزمون دوم] نمرهٔ افرادی که [در آزمون اول] کمترین نمره‌ها را آورده‌اند بهتر می‌شود اما فقط به این دلیل که در آزمون اول احتمال اینکه بدشانسی آورده باشند بیشتر از خوش شانسی آوردن بوده‌است. تا زمانی که نمرات به طور تصادفی تعیین شوند، یا نمرات تغییرات یا خطای تصادفی داشته باشند، نه اینکه بر اساس توانایی تحصیلی دانش آموز تعیین شده باشند یا [به اصطلاح «مقادیری واقعی» نباشند، این پدیده تأثیر خواهد داشت. یکی از اشتباهات متداول از این نظر در آموزش رخ می‌داد. دانش‌آموزانی که به‌خاطر عملکرد خوب تحسین می‌شدند، در اندازه‌گیری‌های بعدی ضعیف‌تر عمل می‌کردند و دانش‌آموزانی که به دلیل عملکرد ضعیف تنبیه می‌شدند، در مرحله بعدی بهتر عمل می‌کردند. بر این اساس آموزگاران تصمیم گرفتند تشویق را کنار بگذارند و تنبیه را ادامه دهند. چنین تصمیمی اشتباه بود، زیرا برگشت به میانگین مبنای علی ندارد، بلکه مبنای آن خطایی تصادفی است حول میانگینی مشخص توزیعی طبیعی دارد.

اگرچه هر یک از اندازه‌گیری‌های حدی به میانگین برمی گردند، نمونه دوم اندازه‌گیری‌ها نسبت نمونهٔ اول به میانگین نزدیک‌تر نخواهد بود. دوباره دانش آموزان را در نظر بگیرید. فرض کنید افراد حدی گرایش داشته باشند تا ۱۰ درصد طول بازه را به سمت میانگینِ ۸۰ برگردند، بنابراین انتظار می‌رود دانش آموزی که روز اول نمره ۱۰۰ را کسب کرده‌است، روز دوم نمرهٔ ۹۸ بیاورد و دانش آموزی که روز اول نمرهٔ ۷۰ آورده‌است انتظار می‌رود در روز دوم امتیاز ۷۱ کسب کند. مقادری مورد انتظار روز دوم نسبت به روز اول به میانگین نزدیک‌ترند. اما نمرات روز دوم در نزدیکی مقادیر مورد انتظار خود قرار خواهند گرفت. برخی بالاتر و برخی پایین‌تر خواهند بود. علاوه بر این، افرادی که نمراتشان به میانگین خیلی نزدیک بوده باید انتظار داشته باشند که از میانگین فاصله بگیرند. این اثر دقیقاً خلاف برگشت به میانگین است و دقیقاً آن را خنثی می‌کند؛ بنابراین انتظار داریم افرادی که نمرات حدی آورده‌اند در روز دوم نمراتی نزدیک تر به میانگین کسب کنند، اما برای همه‌ی افراد، انتظار داریم توزیع فاصله از میانگین در هر دو مجموعهٔ اندازه‌گیری یکسان باشد.

در رابطه با نکته بالا، عملکرد برگشت به میانگین در هر دو جهت به یک اندازه خوب است. انتظار می‌رود دانش آموزی که بالاترین نمرهٔ آزمون را در روز دوم کسب کرده‌است، در روز اول بدتر عمل کرده باشد. همچنین اگر بهترین دانش آموزِ روز اول را با بهترین دانش آموز روز دوم مقایسه کنیم، صرف نظر از اینکه هر دو یک نفر باشند یا خیر، تمایلی برای برگشت به میانگین در هر یک از دو جهت وجود ندارد. انتظار می‌رود که بهترین نمره‌ها در هر دو روز به یک اندازه از میانگین فاصله داشته باشد.

مغالطه‌های برگشت به میانگین

اگر برگشت به میانگین در نظر گرفته نشود، پدیده‌های بسیاری به علل نادرست نسبت داده می‌شوند.

بدترین نمونه از این مغالطه‌ها کتاب هوراس سکریست در سال ۱۹۳۳ با عنوان غلبهٔ میانمایگی در کسب و کار است، این استادِ آمار در کتابش کوهی از داده را جمع‌آوری کرد تا ثابت کند که نرخ سودآوری کسب‌وکارهای رقابتی در طول زمان به سمت میانگین گرایش دارند. در واقع، چنین تأثیری وجود ندارد؛ تغییرات نرخ سودآوری تقریباً در طول زمان ثابت است. سکریست فقط برگشت به میانگین متداول را توصیف کرده بود. یکی از منتقدان خشمگین این اثر به نام هارولد هتلینگ، کتاب سکریست را اینطور توصیف کرده بود: «اثبات جدول ضرب با چیدن تعدادی فیل در ردیف‌ها و ستون‌های مختلف و سپس تکرار همین کار برای چندین حیوان دیگر از گونه‌های مختلف».

مثال دیگری از مغالطهٔ برگشت به میانگین، به احتمال زیاد محاسبات و تفسیر «رتبه‌بندی بهبود» در آزمون‌های آموزشی استاندارد ماساچوست است. در سال ۱۹۹۹، برای مدارس اهداف بهبود خاصی تعیین شد. وزارت آموزش و پرورش تفاوت میانگین نمرات کسب شده توسط دانش آموزان را در سال‌های ۱۹۹۹ و ۲۰۰۰ در جداولی درج کرد. به سرعت مشاهده شد که اکثر مدارسی که بدترین عملکرد را داشتند به اهداف خود دست یافتند، که وزارت آموزش و پرورش آن را به عنوان تأییدی بر درستی سیاست‌های آن‌ها در نظر گرفت. با این حال، همچنین اشاره شد که بسیاری از بهترین مدارس در ایالت‌های مشترک المنافع، مانند دبیرستان بروکلین (با ۱۸ فینالیست بورسیه شایستگی ملی) شکست خورده بودند. این موضوع در بسیاری از نمونه‌های دیگرِ آمار و سیاست عمومی بررسی شده‌است، اما «نمرات بهبود» در سال‌های بعد اعلام نشد و به نظر می‌رسد یافته‌های به دست آمده مصادیقی از برگشت به میانگین باشند.

دانیل کانمن، روان‌شناس، برنده جایزه یادبود نوبل اقتصادی در سال ۲۰۰۲، خاطرنشان کرد که برگشت به میانگین ممکن است دلیل این را که چرا به نظر می‌رسد تنبیه می‌تواند عملکرد را بهبود بخشد، در حالی که به نظر می‌رسد تحسین نتیجه معکوس دارد توضیح دهد.

روزی برای مربیان خلبانی دوره‌ای برگزار می‌کردم و آموزش می‌دادم که برای یادگیری مهارت جدید تشویق از تنبیه اثربخش تر است که با لذت بخش‌ترین تجربهٔ اکتشافی دوران شغلی‌ام مواجه شدم. زمانی که سخنرانی پر شورم به پایان رسید یکی از مربیان کهنه کارِ حاضر دستش را بالا آورد و سخنرانی کوتاه خود را ایراد کرد و گفت تقویت مثبت شاید برای پرندگان مفید باشد اما برای دانشجویان خلبانی نظامی کارایی مطلوبی ندارد. او گفت «در موارد بسیاری دانشجویان خلبانی را برای اجرای بی عیب مانور هوایی تشویق کرده‌ام و در کل وقتی این دانشجویان مانور را تکرار می‌کنند عملکردشان بدتر می‌شود. از طرفی معمولاً بر سر دانشجویانی که عملکرد نامناسب داشته‌اند فریاد زده‌ام و در کل دفعهٔ بعد عملکرد بهتری داشته‌اند. پس خواهش می‌کنم به ما نگویید که تشویق مؤثر است و تنبیه کارایی ندارد چون خلاف آن صادق بوده‌است.» این لحظه بسیار مسرت بخش بود زیرا متوجه حقیقتی مهم در مورد جهان شدم: چون گرایش ما این است که به افراد در ازای عملکرد خوب پاداش دهیم و آن‌ها را در ازای عملکرد تنبیه کنیم و از آنجا که برگشت به میانگین وجود دارد، این بخشی از شرایط انسانی این است که به طور آماری برای پاداش دادن دیگران تنبیه می‌شویم و در ازای تنبیه دیگران پاداش می‌گیریم. بلافاصله آزمایشی را ترتیب دادم که در آن حضار دو سکه را به سمت هدفی در پشت سر خود پرتاب می‌کردند و هیچ بازخوردی نمی‌گرفتند. فاصلهٔ سکه‌ها از هدف را اندازه‌گیری کردیم و دیدیم که افرادی که در تلاش اول بهترین عملکرد را داشتند اغلب در تلاش دوم بدتر شدند و بالعکس. اما می‌دانستم که این آزمایش تأثیر یک عمر قرار گرفتن در معرض شرایطی انحطاطی را از بین نخواهد برد.

مغالطهٔ رگرسیون در کتاب هنر شفاف اندیشیدن نوشتهٔ رولف دوبلی نیز شرح داده شده‌است.

در خط مشی‌های مجریان قانون بریتانیا، نصب دوربین‌های ثبت تخلف ثابت یا متحرک به طور قابل رویت در نقاط سیاه تصادف توصیه شده‌است. توجیه این سیاست بر اساس این تصور است که پس از نصب دوربین، تصادفات رانندگی به طور جدی کاهش می‌یابد. با این حال، متخصصان آمار خاطرنشان کرده‌اند که، اگرچه از لحاظ نجات جان افراد فایدهٔ خالصی وجود داشته‌است، اما عدم در نظر گرفتن اثرات برگشت به میانگین منجر به اغراق این اثرات مفید می‌شود.

تحلیلگران آماری مدت‌هاست که تأثیر برگشت به میانگین در ورزش را تشخیص داده‌اند و حتی نام خاصی برای آن دارند: «پسرفت سال دومی‌ها». مثلاً کارملو آنتونی از تیم دنور ناگتس لیگ NBA در اولین فصل بازی حرفه‌ای خود در سال ۲۰۰۴ فوق‌العاده بود. آنقدر برجسته بود که انتظار نمی‌رفت آن عملکرد را تکرار کند: در سال ۲۰۰۵، شاخص‌های عملکرد آنتونی نسبت به اولین فصل بازی او کاهش پیدا کرد. دلایل «پسرفت سال دومی‌ها» فراوان است و ورزش بر همین فراز و نشیب‌ها متکی است، اما برتری شانسی تازه کاران نیز دلیل مهمی است. برگشت به میانگین در عملکرد ورزشی، برخی از باورهای عامه نظیر «نفرین جراید» و «نفرین میدن» را توضیح دهد. جان هولینگر نام دیگری برای پدیده برگشت به میانگین دارد: «قانون تصادف»، در حالی که بیل جیمز آن را «اصل پلکسی گلاس» می‌نامد.

از آنجایی که افسانه‌های رایج بر وجهی از برگشت به میانگین تمرکز دارند که کاهش عملکرد ورزشکاران از فصلی به فصل دیگر را تبیین می‌کند، معمولاً این واقعیت نادیده گرفته می‌شود که چنین برگشتی می‌تواند عامل بهبود عملکرد نیز باشد. به عنوان مثال، اگر به میانگین ضربه زدن بازیکنان لیگ برتر بیسبال در یک فصل نگاه کنیم، بازیکنانی که میانگین ضربه زدنشان بالاتر از میانگین لیگ بود، در سال بعد به سمت پایین گرایش داشتند، در حالی که گرایش بازیکنان زیر میانگین در سال بعد، روبه رشد و به سمت میانگین بود.

سایر پدیده‌های آماری

مخلص کلام برگشت به میانگین این است که پس از یک رویداد تصادفی حدی، رویداد تصادفی بعدی احتمالاً شدت کمتری خواهد داشت [و عادی تر خواهد بود]. به هیچ وجه رویداد آینده رویداد قبلی را «جبران» یا «خنثی» نمی‌کند، اگرچه این در مغالطهٔ قمارباز (و قانون میانگین‌ها) در نظر گرفته می‌شود. به طور مشابه، قانون اعداد بزرگ بیان می‌کند که در بلندمدت، میانگین به سمت امید ریاضی می‌رود، اما در مورد آزمایش‌های فردی هیچ اظهارنظری نمی‌کند. به عنوان مثال، پس از آمدن ۱۰ شیر در پرتاب سکه‌ای عادی (رویدادی نادر و شدید)، برگشت به میانگین بیان می‌کند که دور بعدی احتمالاً تعداد شیر کمتر از ۱۰ خواهد بود، در حالی که قانون اعداد بزرگ بیان می‌کند که در درازمدت، این رویداد احتمالاً به سمت میانگین تعدیل می‌شود و سهم شیر به طور میانگین به ۱/۲ گرایش پیدا می‌کند. در مقابل، در مغالطه قمارباز به اشتباه فرض می‌شود که پرتاب‌های بعدی سکه برای ایجاد توازن الزاماً یک سری خط خواهد بود.

معکوس این اثر، میانگین گریزی است که در هر توزیعی با چگالی احتمال غیرصفر تا بی‌نهایت رخ می‌دهد.

تعریف برای رگرسیون خطی سادهٔ نقاط داده

این تعریف برگشت به میانگین است که دقیقاً از کاربرد اصلی سر فرانسیس گالتون پیروی می‌کند.

فرض کنید تعداد n داده { y_i, x_i } داشته باشیم، که i = ۱، ۲، ...، n. می‌خواهیم معادله خط رگرسیون را پیدا کنیم که خطی مستقیم است:

$y=\alpha +\beta x,\,$

این معادله «بهترین» برازش را برای نقاط داده فراهم می‌کند. (توجه داشته باشید که یک خط مستقیم ممکن است منحنی رگرسیون مناسب برای نقاط داده داده شده نباشد) در اینجا «بهترین» با رویکرد حداقل مربعات استنباط می‌شود: خطی که مجموع مجذور باقیمانده‌های مدل رگرسیون خطی را به حداقل می‌رساند. به عبارت دیگر، اعداد α و β مشکل کمینه سازی زیر را حل می‌کنند:

پیدا کردن $\min _{\alpha ,\,\beta }Q(\alpha ,\beta )$ ، که $Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\$

با استفاده از محاسبات دیفرانسیل و انتگرال می‌توان نشان داد که مقادیر α و β که تابع هدف Q را به حداقل می‌رسانند عبارتند از:

${\begin{aligned}&{\hat {\beta }}={\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}={\frac {{\overline {xy}}-{\bar {x}}{\bar {y}}}{{\overline {x^{2}}}-{\bar {x}}^{2}}}={\frac {\operatorname {Cov} [x,y]}{\operatorname {Var} [x]}}=r_{xy}{\frac {s_{y}}{s_{x}}},\\&{\hat {\alpha }}={\bar {y}}-{\hat {\beta }}\,{\bar {x}},\end{aligned}}$

که r_xy ضریب همبستگی نمونه بین x و y است، s_x انحراف معیار x, و s_y انحراف معیار y است. منظور از خط افقی روی متغیر، میانگین نمونه آن متغیر است. مثلا: ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$

با جایگزینی عبارات بالا به جای ${\hat {\alpha }}$ و ${\hat {\beta }}$ در$y=\alpha +\beta x,\,$ مقادیر برازش شده به دست می‌آید:

${\hat {y}}={\hat {\alpha }}+{\hat {\beta }}x,\,$

که می‌دهد:

${\frac {{\hat {y}}-{\bar {y}}}{s_{y}}}=r_{xy}{\frac {x-{\bar {x}}}{s_{x}}}$

می‌توان نقش r _xy در خط رگرسیون نقاط داده استاندارد شده را در معادلهٔ بالا مشاهده کرد.

اگر r_xy بین ۱ و -۱ باشد می‌گوییم که داده‌ها برگشت به میانگین را نشان می‌دهند. به عبارت دیگر، اگر رگرسیون خطی مدل مناسبی برای مجموعه‌ای از نقاط داده باشد که ضریب همبستگی نمونه آن کامل نیست، آنگاه رگرسیون به سمت میانگین وجود دارد. مقدار استاندارد پیش‌بینی‌شده (یا برازش) y به میانگین آن نزدیک‌تر است تا مقدار استاندارد شده x به میانگین آن.

تعاریف توزیع دو متغیره با توزیع‌های حاشیه‌ای یکنواخت

تعریف خاص

فرض کنید X ₁, X ₂ متغیرهای تصادفی با توزیع حاشیه‌ای یکسان با میانگین μ باشند. در این چهارچوب گفته می‌شود که در توزیع دو متغیره X ₁ و X ₂ برگشت به میانگین قابل مشاهده است اگر، برای هر عدد c > μ داشته باشیم:

μ ≤ E[X₂ | X₁ = c] < c,

و عکس این نامعادله برای c < μ نیز صادق است.

در ادامه توضیحی غیررسمی از تعریف فوق ارائه شده‌است. جامعه‌ای آماری ااز یک محصول خاص را در نظر بگیرید. هر محصول دارای دو مقدار عددی X ₁ و X ₂ است (مثلاً سطح نیمهٔ چپ آن (X ₁) و سطح نیمهٔ راست آن (X ₂) باشد). فرض کنید که X ₁ و X ₂ توزیع احتمال یکسانی دارند و میانگین X ₁ و X ₂ هر دو μ هستند. اکنون یک محصول تصادفی از جمعیت انتخاب می‌شود و مقدار X ₁ آن را با c نشان می‌دهیم (توجه داشته باشید که c ممکن است بزرگتر، مساوی یا کوچکتر از μ باشد). هنوز به مقدار X ₂ این محصول دسترسی نداریم. مقدار مورد انتظار X ₂ این محصول خاص را با d نشان می‌دهیم. (یعنی فرض کنید d مقدار میانگین X ₂ همه محصولاتی در جامعه آماری باشد که مقدار X₁ آن‌ها c باشد). اگر شرط زیر درست باشد:

مقدار c هر چه باشد، d بین μ و c قرار می‌گیرد (یعنی d به μ نزدیکتر از c است)

بنابرین می‌گوییم که X ₁ و X ₂ برگشت به میانگین را نشان می‌دهند.

این تعریف دقیقاً با کاربرد متداول کنونی که بر پایهٔ شیوهٔ استفادهٔ اصلی گالتون از اصطلاح «برگشت به میانگین» تکامل یافته مطابقت دارد. تعریف کنونی «تعریفی خاص» است به این معنا که هر توزیع دو متغیره که توزیع‌های حاشیه‌ای یکسان داشته باشد، برگشت به میانگین را نشان نمی‌دهد (با توجه به این تعریف).

قضیه

اگر زوج (X , Y) متشکل از دو متغیرهای تصادفی از توزیع نرمال دو متغیره پیروی کند، آنگاه میانگین شرطی E(Y | X) تابع خطی X است. ضریب همبستگی r بین X و Y به همراه میانگین‌های و واریانس‌های حاشیه‌ای X و Y، این رابطه خطی را تعیین می‌کنند:

${\frac {E(Y\mid X)-E[Y]}{\sigma _{y}}}=r{\frac {X-E[X]}{\sigma _{x}}},$

که در آن E[X] و E[Y] به ترتیب امید ریاضی X و Y و σ _x و σ _y به ترتیب انحراف از معیار X و Y هستند.

از این رو امید ریاضی شرطی Y، با شرط اینکه X از میانگین خود به مقدار t انحراف از معیار بیشتر باشد (که حالتی را که کمتر از میانگین باشد را نیز در صورت t < 0 شامل می‌شود)، به مقدار rt انحراف استاندارد بیشتر از میانگین Y خواهد بود. از آنجا که |r| کوچکتر یا مساوی ۱ است، فاصلهٔ Y از میانگین از فاصلهٔ X از میانگین بیشتر نیست و این فاصله بر اساس ضریبی از انحرافات از معیار اندازه‌گیری می‌شود.

بنابراین، اگر مقدار r بزرگتر یا مساوی صفر و کوچکتر از یک باشد، آنگاه (X , Y) برگشت به میانگین را نشان می‌دهد (بر اساس این تعریف).

تعریف عام

ساموئلز تعریف زیر را برای برگشت به میانگین ارائه کرد تا جایگزینی برای تعریف خاص برگشت به میانگین باشد که در بالا اشاره شد.

فرض کنید X ₁, X ₂ متغیرهای تصادفی با توزیع حاشیه‌ای یکسان و میانگین μ باشند. در این چهارچوب بندی گفته می‌شود توزیع دو متغیره X ₁ و X ₂ برگشت به میانگین نشان می‌دهد اگر برای هر عدد c داشته باشیم:

μ ≤ E[X₂ | X₁ > c] < E[X₁ | X₁ > c], و

μ ≥ E[X₂ | X₁ < c] > E[X₁ | X₁ < c]

این تعریف «عام» است به این معنا که هر توزیع دو متغیره با توزیع‌های حاشیه‌ای یکسان، برگشت به میانگین را نشان می‌دهد، مشروط بر اینکه برخی شروط ضعیف برآورده شوند (طبق توضیحات ارائه شده در مقاله ساموئلز این شروط عبارتند از نبود تبهگنی و وابستگی مثبت ضعیف).

تعریف جایگزین در کاربرد مالی

جرمی سیگل از اصطلاح «برگشت به میانگین» برای توصیف سری زمانی مالی خاصی استفاده می‌کند که در آن «ممکن است بازده در کوتاه‌مدت بسیار ناپایدار اما در بلندمدت بسیار پایدار باشد». از نظر کمی، انحراف معیار میانگین بازده سالانه سریع‌تر از معکوس دوره نگهداری کاسته می‌شود، و به طور ضمنی استنباط می‌شود که این فرایند ولگشت نیست، بلکه به شکلی نظام مند پس از دوره‌هایی که در آن‌ها بازده کمتر کسب شده‌است، دوره‌هایی جبرانی با بازده بالاتر می‌آیند. نمونهٔ آن در بسیاری از مشاغل فصلی مشاهده می‌شود.

جستارهای وابسته

• اصل هاردی واینبرگ
• اعتبار درونی
• قانون اعداد بزرگ
• مارتینگل (نظریه احتمال)
• رقیق شدن رگرسیون
• سوگیری انتخاب