هزار مقدار اولیه
φ
(
n
)
{\displaystyle \varphi (n)}
در نظریه اعداد تابع فی اویلر یا
φ
(
n
)
{\displaystyle \varphi (n)}
n که نسبت به n اول اند را میشمارد. اگر n یک عدد طبیعی مثبت باشد، آنگاه
φ
(
n
)
{\displaystyle \varphi (n)}
k در بازه ۱ تا n بهطوریکه بزرگترین مقسومعلیه مشترک (ب.م.م) n و k برابر ۱ باشد.
تابع فی اویلر یک تابع ضربی است، بدین معنی که اگر دو عدد m و n نسبت به هم اول باشند آنگاه
φ
(
m
n
)
=
φ
(
m
)
φ
(
n
)
{\displaystyle \varphi (mn)=\varphi (m)\varphi (n)}
تابع فی اویلر نقش کلیدی در تعریف سیستم رمزنگاری RSA دارد.
تاریخچه و نمادگذاری [ ویرایش ] لئونارد اولر این تابع را در سال ۱۷۶۳ معرفی کرد. در آن زمان او هنوز نماد خاصی برای این تابع تعیین نکرده بود. بعدها لئونارد اویلر با مطالعه بیشتر تابع فی، حرف یونانی π را برای آن برگزید. نماد استاندارد φ بعدها توسط گاوس استفاده شدهاست.
محاسبه مقدار تابع فی [ ویرایش ] چندین راه برای محاسبه این فرمول وجود دارد.
فرمول ضرب اویلر [ ویرایش ] این تابع بیان میکند که:
φ
(
n
)
=
n
∏
p
∣
n
(
1
−
1
p
)
{\displaystyle \varphi (n)=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right)}
که در آن
p
{\displaystyle p}
عدد اول است بهطوریکه
n
{\displaystyle n}
p
{\displaystyle p}
تبدیل فوریه [ ویرایش ] مقدار تابع فی برابر است با مقدار تبدیل فوریه گسسته ب.م.م در ۱ یعنی:
F
{
x
}
[
m
]
=
∑
k
=
1
n
x
k
⋅
e
−
2
π
i
m
k
n
,
x
=
{
gcd
(
k
,
n
)
}
for
k
∈
{
1
…
n
}
φ
(
n
)
=
F
{
x
}
[
1
]
=
∑
k
=
1
n
gcd
(
k
,
n
)
e
−
2
π
i
k
n
.
{\displaystyle {\begin{aligned}{\mathcal {F}}\left\{\mathbf {x} \right\}[m]&=\sum \limits _{k=1}^{n}x_{k}\cdot e^{{-2\pi i}{\frac {mk}{n}}},\mathbf {x} =\left\{\gcd(k,n)\right\}\quad {\text{for}}\,k\in \left\{1\dots n\right\}\\\varphi (n)&={\mathcal {F}}\left\{\mathbf {x} \right\}[1]=\sum \limits _{k=1}^{n}\gcd(k,n)e^{{-2\pi i}{\frac {k}{n}}}.\end{aligned}}}
مقدار حقیقی این فرمول برابر است با:
φ
(
n
)
=
∑
k
=
1
n
gcd
(
k
,
n
)
cos
2
π
k
n
.
{\displaystyle \varphi (n)=\sum \limits _{k=1}^{n}\gcd(k,n)\cos {2\pi {\frac {k}{n}}}.}
توجه کنید که برخلاف دو فرمول دیگر در این فرمول نیازی به دانستن عوامل اول n نیست. اما چون فرمول شامل محاسبه ب.م.م n و همه اعداد مثبت کمتر از n است در نهایت به تجزیه n نیاز خواهیم داشت.
جمع مقسوم علیهها [ ویرایش ] فرمول کلاسیک اویلر
∑
d
∣
n
φ
(
d
)
=
n
,
{\displaystyle \sum _{d\mid n}\varphi (d)=n,}
این فرمول به روشهای مختلف قابل اثبات است.
برای n>1 میتوان تابع فی را به عنوان یک حد تابع زتای ریمان محاسبه کرد
φ
(
n
)
=
n
lim
s
→
1
ζ
(
s
)
∑
d
|
n
μ
(
d
)
(
e
1
/
d
)
(
s
−
1
)
{\displaystyle \varphi (n)=n\lim \limits _{s\rightarrow 1}\zeta (s)\sum \limits _{d|n}\mu (d)(e^{1/d})^{(s-1)}}
که در این فرمول
ζ
(
s
)
{\displaystyle \zeta (s)}
تابع زتای ریمان است،
μ
{\displaystyle \mu }
تابع موبیوس است،
e
{\displaystyle e}
نپر است،
و d مقسوم علیه است.
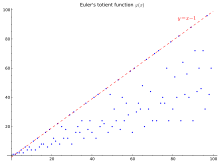
چند مقدار تابع [ ویرایش ] ۹۹ مقدار اولیه این تابع در جدول و نمودار زیر قابل مشاهده است.
Graph of the first 100 values
φ
(
n
)
{\displaystyle \varphi (n)}
+۰
+۱
+۲
+۳
+۴
+۵
+۶
+۷
+۸
+۹
۰+
۱
۱
۲
۲
۴
۲
۶
۴
۶
۱۰+
۴
۱۰
۴
۱۲
۶
۸
۸
۱۶
۶
۱۸
۲۰+
۸
۱۲
۱۰
۲۲
۸
۲۰
۱۲
۱۸
۱۲
۲۸
۳۰+
۸
۳۰
۱۶
۲۰
۱۶
۲۴
۱۲
۳۶
۱۸
۲۴
۴۰+
۱۶
۴۰
۱۲
۴۲
۲۰
۲۴
۲۲
۴۶
۱۶
۴۲
۵۰+
۲۰
۳۲
۲۴
۵۲
۱۸
۴۰
۲۴
۳۶
۲۸
۵۸
۶۰+
۱۶
۶۰
۳۰
۳۶
۳۲
۴۸
۲۰
۶۶
۳۲
۴۴
۷۰+
۲۴
۷۰
۲۴
۷۲
۳۶
۴۰
۳۶
۶۰
۲۴
۷۸
۸۰+
۳۲
۵۴
۴۰
۸۲
۲۴
۶۴
۴۲
۵۶
۴۰
۸۸
۹۰+
۲۴
۷۲
۴۴
۶۰
۴۶
۷۲
۳۲
۹۶
۴۲
۶۰
خط y = n-1 یک کران بالا برای تابع است و زمانی رخ میدهد که n اول باشد.
بیان میکند: اگر n و a نسبت به هم اول باشند آنگاه
a
φ
(
n
)
≡
1
mod
n
.
{\displaystyle a^{\varphi (n)}\equiv 1\mod n.\,}
در حالت خاصی که n عدد اول باشد این قضیه به قضیه کوچک فرما معروف است.
این قضیه از قضیه لاگرانژ نتیجه میشود.
سیستم رمزنگاری RSA بر روی همین قضیه بنا شده است: بیان میکنید که معکوس تابع
a
↦
a
d
mod
n
{\displaystyle a\mapsto a^{d}\mod n}
b
↦
b
e
mod
n
{\displaystyle b\mapsto b^{e}\mod n}
معکوس ضربی d به پیمانه
φ
(
n
)
{\displaystyle \varphi (n)}
دیگر فرمولهای مرتبط با
φ
(
n
)
{\displaystyle \varphi (n)}
[ ویرایش ]
a
∣
b
{\displaystyle a\mid b}
φ
(
a
)
∣
φ
(
b
)
.
{\displaystyle \varphi (a)\mid \varphi (b).}
n
∣
φ
(
a
n
−
1
)
{\displaystyle n\mid \varphi (a^{n}-1)}
a , n > 1)
φ
(
m
n
)
=
φ
(
m
)
φ
(
n
)
⋅
d
φ
(
d
)
{\displaystyle \varphi (mn)=\varphi (m)\varphi (n)\cdot {\frac {d}{\varphi (d)}}}
d = gcd(m , n ).
φ
(
2
m
)
=
{
2
φ
(
m
)
if
m
is even
φ
(
m
)
if
m
is odd
{\displaystyle \varphi (2m)={\begin{cases}2\varphi (m)&{\text{ if }}m{\text{ is even}}\\\varphi (m)&{\text{ if }}m{\text{ is odd}}\end{cases}}}
φ
(
n
m
)
=
n
m
−
1
φ
(
n
)
.
{\displaystyle \;\varphi \left(n^{m}\right)=n^{m-1}\varphi (n).}
φ
(
l
c
m
(
m
,
n
)
)
⋅
φ
(
g
c
d
(
m
,
n
)
)
=
φ
(
m
)
⋅
φ
(
n
)
.
{\displaystyle \varphi (\mathrm {lcm} (m,n))\cdot \varphi (\mathrm {gcd} (m,n))=\varphi (m)\cdot \varphi (n).}
∑
d
∣
n
μ
2
(
d
)
φ
(
d
)
=
n
φ
(
n
)
{\displaystyle \sum _{d\mid n}{\frac {\mu ^{2}(d)}{\varphi (d)}}={\frac {n}{\varphi (n)}}}
∑
1
≤
k
≤
n
(
k
,
n
)
=
1
k
=
1
2
n
φ
(
n
)
for
n
>
1
{\displaystyle \sum _{1\leq k\leq n \atop (k,n)=1}\!\!k={\frac {1}{2}}n\varphi (n){\text{ for }}n>1}
∑
k
=
1
n
φ
(
k
)
=
1
2
(
1
+
∑
k
=
1
n
μ
(
k
)
⌊
n
k
⌋
2
)
{\displaystyle \sum _{k=1}^{n}\varphi (k)={\frac {1}{2}}\left(1+\sum _{k=1}^{n}\mu (k)\left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right)}
∑
k
=
1
n
φ
(
k
)
k
=
∑
k
=
1
n
μ
(
k
)
k
⌊
n
k
⌋
=
6
π
2
n
+
O
(
(
log
n
)
2
/
3
(
log
log
n
)
4
/
3
)
{\displaystyle \sum _{k=1}^{n}{\frac {\varphi (k)}{k}}=\sum _{k=1}^{n}{\frac {\mu (k)}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+{\mathcal {O}}\left((\log n)^{2/3}(\log \log n)^{4/3}\right)}
∑
k
=
1
n
k
φ
(
k
)
=
315
ζ
(
3
)
2
π
4
n
−
log
n
2
+
O
(
(
log
n
)
2
/
3
)
{\displaystyle \sum _{k=1}^{n}{\frac {k}{\varphi (k)}}={\frac {315\zeta (3)}{2\pi ^{4}}}n-{\frac {\log n}{2}}+{\mathcal {O}}\left((\log n)^{2/3}\right)}
اشنایدر دو رابطه پیدا کرد که نسبت طلایی و تابع فی و تابع موبیوس را به هم مرتبط میکرد.
در فرمولهای زیر
ϕ
=
1
+
5
2
=
1.618
…
{\displaystyle \phi ={\frac {1+{\sqrt {5}}}{2}}=1.618\dots }
این روابط به صورت زیر هستند:
ϕ
=
−
∑
k
=
1
∞
φ
(
k
)
k
log
(
1
−
1
ϕ
k
)
{\displaystyle \phi =-\sum _{k=1}^{\infty }{\frac {\varphi (k)}{k}}\log \left(1-{\frac {1}{\phi ^{k}}}\right)}
1
ϕ
=
−
∑
k
=
1
∞
μ
(
k
)
k
log
(
1
−
1
ϕ
k
)
.
{\displaystyle {\frac {1}{\phi }}=-\sum _{k=1}^{\infty }{\frac {\mu (k)}{k}}\log \left(1-{\frac {1}{\phi ^{k}}}\right).}
از کم کردن این دو نتیجه میشود
∑
k
=
1
∞
μ
(
k
)
−
φ
(
k
)
k
log
(
1
−
1
ϕ
k
)
=
1.
{\displaystyle \sum _{k=1}^{\infty }{\frac {\mu (k)-\varphi (k)}{k}}\log \left(1-{\frac {1}{\phi ^{k}}}\right)=1.}
با اعمال تابع نمایی به هر دو طرف رابطه به یک رابطه برای عدد نپر میرسیم
e
=
∏
k
=
1
∞
(
1
−
1
ϕ
k
)
μ
(
k
)
−
φ
(
k
)
k
.
{\displaystyle e=\prod _{k=1}^{\infty }\left(1-{\frac {1}{\phi ^{k}}}\right)^{\frac {\mu (k)-\varphi (k)}{k}}.}
اثبات بر پایه دو فرمول زیر است:
∑
k
=
1
∞
φ
(
k
)
k
(
−
log
(
1
−
x
k
)
)
=
x
1
−
x
{\displaystyle \sum _{k=1}^{\infty }{\frac {\varphi (k)}{k}}(-\log(1-x^{k}))={\frac {x}{1-x}}}
∑
k
=
1
∞
μ
(
k
)
k
(
−
log
(
1
−
x
k
)
)
=
x
,
{\displaystyle \sum _{k=1}^{\infty }{\frac {\mu (k)}{k}}(-\log(1-x^{k}))=x,}
سری دیریکله برای تابع فی را میتوان بر حسب جملات تابع زتای ریمان به صورت زیر نوشت
∑
n
=
1
∞
φ
(
n
)
n
s
=
ζ
(
s
−
1
)
ζ
(
s
)
.
{\displaystyle \sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}.}
همچنین تابع مولد سری لامبرت به صورت زیر است
∑
n
=
1
∞
φ
(
n
)
q
n
1
−
q
n
=
q
(
1
−
q
)
2
{\displaystyle \sum _{n=1}^{\infty }{\frac {\varphi (n)q^{n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}}
که در ان اندازه q کمتر از ۱ است.
هر دو روابط بالا با استفاده ضرب سریهای پایه و با استفاده از فرمولهای محاسبه تابع فی قابل اثبات هستند.
نسبت دو جمله متوالی [ ویرایش ] در سال ۱۹۵۰ سومایاجولو اثبات کرد
lim
inf
φ
(
n
+
1
)
φ
(
n
)
=
0
{\displaystyle \lim \inf {\frac {\varphi (n+1)}{\varphi (n)}}=0}
و
lim
sup
φ
(
n
+
1
)
φ
(
n
)
=
∞
.
{\displaystyle \lim \sup {\frac {\varphi (n+1)}{\varphi (n)}}=\infty .}
رمزنگاری RSA [ ویرایش ] در سیستم RSA ابتدا دو عدد اول بزرگ p و q را انتخاب میکنیم. سپس مقادیر n=pq و k=
φ
(
n
)
{\displaystyle \varphi (n)}
یک پیام مانند عدد مثبت m به صورت S = me mod n رمزگذاری میشود.
برای رمزگشایی مقدار t = Sd mod n محاسبه میشود. قضیه اویلر نشان میدهد که اگر t کمتر از n باشد آنگاه t=m.
سیستم RSA به خطر خواهد افتاد اگر بتوانیم عدد n را تجزیه کنیم یا بتوانیم مقدار تابع فی را بدون تجزیه n بدست بیاوریم.
مسئلههای حل نشده [ ویرایش ] اگر p اول باشد آنگاه
φ
(
p
)
=
p
−
1
{\displaystyle \varphi (p)=p-1}
آیا عدد مرکب n وجود دارد بهطوریکه
φ
(
n
)
|
n
−
1
{\displaystyle \varphi (n)|n-1}
در سال ۱۹۳۳ لیمر اثبات کرد که اگر n وجود داشته باشد آنگاه حتماً باید فرد باشد و باید حداقل ۷ عامل اول داشته باشد. در سال ۱۹۸۰ کوهن و هاگیس اثبات کردند که n>1020 و باید حداقل ۱۴ عامل اول داشته باشد. بعدها هاگیس نشان داد که اگر n بر ۳ بخش پذیر باشد آنگاه n>101937042 و باید حداقل ۲۹۸۸۴۷ عامل اول داشته باشد.
حدس کارمایکل [ ویرایش ] حدس: هیچ عددی مانند n وجود ندارد بهطوریکه برای هر عدد دیگر مانند m داشته باشیم
φ
(
n
)
!
=
φ
(
m
)
{\displaystyle \varphi (n)!=\varphi (m)}
مثال نقض برای این گزاره پیدا شود آنگاه میتوان نشان داد که بینهایت مثال نقض برای این گزاره وجود دارد.
میتوان نشان داد که کوچکترین مثال نقض برای این گزاره در مبنای ۱۰ بیش از ۱۰ میلیارد رقم دارد.
جستارهای وابسته [ ویرایش ]







![{\displaystyle {\begin{aligned}{\mathcal {F}}\left\{\mathbf {x} \right\}[m]&=\sum \limits _{k=1}^{n}x_{k}\cdot e^{{-2\pi i}{\frac {mk}{n}}},\mathbf {x} =\left\{\gcd(k,n)\right\}\quad {\text{for}}\,k\in \left\{1\dots n\right\}\\\varphi (n)&={\mathcal {F}}\left\{\mathbf {x} \right\}[1]=\sum \limits _{k=1}^{n}\gcd(k,n)e^{{-2\pi i}{\frac {k}{n}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb6e9b0bca4db124c0da54548202dfffecdcb87)


































