شبه گروه: تفاوت میان نسخه‌ها

محتوای حذف‌شده محتوای افزوده‌شده

درخط

نسخهٔ ‏۲۶ دسامبر ۲۰۱۹، ساعت ۱۹:۵۶

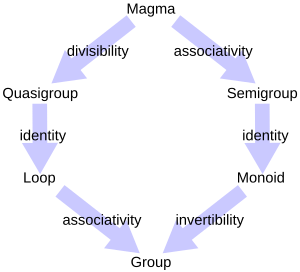
ساختارهای شبیه گروه
	کلی^α	شرکت‌پذیری	همانی	معکوس‌پذیری	جابجاپذیری
نیم-گروهوار
رسته کوچک
گروهوار
ماگما
شبه گروه
مگامای یکه
لوپ
نیم-گروه
نیم-گروه معکوس
تکوار
تکوار جابجایی
گروه
گروه آبلی
^ بستار، که در بسیاری از منابع استفاده شده است، اصول موضوعه ای معادل با کلی بودن (totality) است، هرچند به صورت متفاوتی تعریف شده است.

در ریاضیات، به ویژه در جبر انتزاعی، یک شبه‌گروه یک ساختار جبری است که شبیه گروه است به این معنا که " تقسیم " همیشه امکان پذیر است. شبه‌گروه‌ها از نظر گروه‌های مختلف تفاوت زیادی دارند زیرا لزوماً به هم وابسته نیستند .

یک شبه‌گروه با یک عنصر هویتی حلقه نامیده می شود .

تعاریف

حداقل دو تعریف رسمی از نظر ساختاری معادل شبه‌گروه وجود دارد. یکی شبه‌گروه را به عنوان یک مجموعه با یک عملیات دودویی تعریف می کند، و دیگری، از دید جبر جهانی، شبه گروه را به عنوان سه عملیات ابتدایی تعریف می کند. تصویر همگن از یک شبه‌گروه تنها با یک عمل باینری تعریف شده‌است ،هرچند، نیاز نیست شبه‌گروه باشد. ^[۱] ما با تعریف اول شروع می کنیم.

جبر

یک شبه‌گروه (Q, ∗) مجموعه ای همچون Q است، با یک عمل باینری ∗، (یعنی یک ماگما)، و از ویژگی مربع لاتین تبعیت می‌کند . این بیان می‌کند که، برای هر a و b در Q، عناصر منحصر به فرد x و y در Q وجود دارد به طوری که هر دو

a ∗ x = b ،

y ∗ a = b

نگه می‌دارد. (به عبارت دیگر: هر عنصر مجموعه دقیقاً یک بار در هر سطر و دقیقاً یک بار در هر ستون جدول ضرب چهارگوش یا جدول کایلی اتفاق می افتد. این ویژگی تضمین می‌کند که جدول کایلی از یک شبه‌گروه محدود یک مربع لاتین است) نیازمندی منحصر به فرد را می توان با نیازمندی‌ای جایگزین کرد که ماگما باشد و خاصیت لغو داشته‌باشد. ^[۲]

راه‌حل‌های منحصر به فرد برای این معادلات x = a \ b و y = b / a عنوان شده. عملیات "\" و "/" به ترتیب تقسیم چپ و راست خوانده می شوند .

مجموعه خالی مجهز به عملكرد دودویی خالی این تعریف از شبه‌گروه را برآورده می كند. برخی از نویسندگان گروه چهارجانبه خالی را می پذیرند اما برخی دیگر صریحاً آن را رد نمی کنند. ^[۳] ^[۴]

جبر جهانی

با توجه به برخی از ساختارهای جبری ، یک هویت معادله ای است که در آن کلیه متغیرها بطور ضمنی در سطح جهانی قرار می گیرند ، و در آن کلیه عملیات ها از جمله اقدامات ابتدایی متناسب با ساختار هستند. ساختارهای جبری صرفاً با هویتها اكسیوماتيزه می شوند و انواع مختلفی ناميده می شوند. بسیاری از نتایج استاندارد در جبر جهانی فقط مربوط به انواع است. اگر تقسیمات چپ و راست به عنوان ابتدایی در نظر گرفته شود ، تعداد چهار گروه مختلف هستند.

گروه چهار گانه (Q, ∗, \, /) نوعی جبر (2،2،2) است (یعنی مجهز به سه عملیات دودویی) که هویت را راضی می کند:

y = x ∗ ( x \ y ) ،

y = x \ ( x ∗ y ) ،

y = ( y / x ) ∗ x ،

y = ( y ∗ x ) / x .

به عبارت دیگر: ضرب و تقسیم به هر ترتیب ، یکی پس از دیگری ، در یک طرف توسط همان عنصر ، اثر خالص ندارند.

از این رو اگر (Q, ∗) طبق تعریف اول ، یک گروه چهار جانبه باشد ، (Q, ∗, \, /) همان quasigrup گروه به معنای جبر جهانی است.

یک حلقه است quasigroup با یک هویت عنصراست که یک عنصر eطوری که

x ∗ e = x و e ∗ x = x برای همه x در Q.

از این رو نتیجه می گیرد که عنصر هویت ، e ، منحصر به فرد است ، و هر عنصر Q وارونه های منحصر به فرد چپ و راست دارد (که لازم نیست یکسان باشند). از آنجا که حضور یک عنصر هویت ضروری است ، یک حلقه نمی تواند خالی باشد.

یک گروه شبه قشر با یک عنصر قدرتمند به نام پیک ("quasigroup idempotent اشاره شده") نامیده می شود. این یک مفهوم ضعیف تر از یک حلقه است اما با این وجود متداول است زیرا ، به عنوان مثال ، با توجه به یک گروه abelian ، (A, +) ، با انجام عمل تفریق خود به عنوان ضرب quasigroup ، پیک (A, −) با هویت گروه (صفر) می چرخاند. به یک "پرهیزکار" اشاره کرد. (یعنی ایزوتوپی اصلی (x, y, z) ↦ (x, −y, z) . )

حلقه ای که به صورت گروهی باشد ، گروهی است. یک گروه می تواند یک ایزوتوپ پیک غیر انجمنی داشته باشد ، اما نمی تواند یک ایزوتوپ حلقه غیر اجتماعی داشته باشد.

خواص ارتباط ضعیف تری وجود دارد که به آنها اسامی خاصی داده شده است.

به عنوان مثال ، یک حلقه Bol یک حلقه است که هم راضی می کند:

x ∗ ( y ∗ ( x ∗ z )) = ( x ∗ ( y ∗ x )) ∗ z برای هر x ، y و z در Q (یک حلقه بول سمت چپ ) ،

یا یه چیز دیگه

(( z ∗ x ) ∗ y ) ∗ x = z ∗ (( x ∗ y ) ∗ x ) برای هر x ، y و z در Q (یک حلقه Bol مناسب ).

یک حلقه که هم حلقه بول سمت چپ و هم راست است یک حلقه موفانگ است . این معادل با هرکدام از هویتهای موفنگ مجرد زیر برای همه x ، y ، z است :

x ∗ ( y ∗ ( x ∗ z )) = (( x ∗ y ) ∗ x ) ∗ z ،

z ∗ ( x ∗ ( y ∗ x )) = (( z ∗ x ) ∗ y ) ∗ x ،

( x ∗ y ) ∗ ( z ∗ x ) = x ∗ (( y ∗ z ) ∗ x ) ، یا

( x ∗ y ) ∗ ( z ∗ x ) = ( x ∗ ( y ∗ z )) ∗ x .

تقارن

اسمیت (2007) خصوصیات و زیر کلاسهای مهم زیر را نام می برد:

تقارن

اگر هویت معادل زیر وجود داشته باشد ، یک گروه چهار نیم قطبی است:

xy = y / x ،

yx = x \ y ،

x = ( yx ) y ،

x = y ( xy ).

اگر چه ممکن است این آموزش به نظر می رسد خاص، هر quasigroup Q باعث که quasigroup semisymmetric Q Δ بر روی محصول مستقیم مکعب Q ³ از طریق عملیات زیر:

(x_{1},x_{2},x_{3})\cdot (y_{1},y_{2},y_{3})=(y_{3}/x_{2},y_{1}\backslash x_{3},x_{1}y_{2})=(x_{2}//y_{3},x_{3}\backslash \backslash y_{1},x_{1}y_{2}),

که در آن "//" و "\\" عملیات تقسیم مزدوج هستند که توسط آنها داده شده است  $y//x=x/y$  و  $y\backslash \backslash x=x\backslash y$  .

محاکمه

تقارن کل

کلاس باریک که یک گروه شبه کاملاً متقارن است (گاهی اوقات به اختصار TS-quasigroup ) که در آن همه ترکیبات همزمان با یک عمل همزمان می شوند: xy = x / y = x \ y . روش دیگر برای تعریف (همان مفهوم) quasigroup کاملاً متقارن به عنوان یک کوآیگرمی نیمه متقارن است که همچنین قابل تبادل است ، یعنی xy = yx .

چهارگوشه های متقارن کل Idempotent دقیقاً (به عنوان مثال در یک زندگی با) سه برابر اشتاینر است ، بنابراین چنین کوآییگروگ quasigroup اشتاینر نیز نامیده می شود ، و گاهی اوقات حتی به صورت مختصر با مخلوط اسکواپ نیز شناخته می شود . اصطلاح sloop به طور مشابه برای یک کوآیی گروپ اشتاینر نیز تعریف شده است. بدون idempotency ، شبه گروههای متقارن کل مطابق با مفهوم هندسی سه گانه گسترش یافته اشتاینر ، همچنین به نام منحنی کربن بیضوی کلیت (GECC) نامیده می شوند.

ضد تقارن کل

گروه چهارم (Q, ∗) کاملاً ضد متقارن نامیده می شود ، اگر برای همه c, x, y ∈ Q ، هر دو پیامد زیر وجود داشته باشد: ^[۵]

( c ∗ x ) ∗ y = ( c ∗ y ) ∗ x دلالت بر x = y دارد
x ∗ y = y ∗ x دلالت دارد که x = y .

اگر فقط اولین پیامد داشته باشد ، کاملاً ضد متقارن نامیده می شود. ^[۵]

این ویژگی به عنوان مثال در الگوریتم Damm مورد نیاز است .

مثال ها

هر گروه یک حلقه a ∗ x = b زیرا a ∗ x = b اگر و تنها اگر x = a⁻¹ ∗ b و y ∗ a = b اگر و تنها اگر y = b ∗ a⁻¹
اعداد صحیح Z با تفریق (-) یک گروه چهار نفره را تشکیل می دهند.
معقولات غیرzero Q ^× (یا واقعیت های nonzero R ^× ) با تقسیم (÷) یک گروه چهار نفری را تشکیل می دهند.
هر فضای برداری بیش از یک حوزه از مشخصه به 2 فرم برابر یک idempotent ، جابجایی تحت عملیات x ∗ y = (x + y) / 2 quasigroup.
هر سیستم سه گانه اشتاینر این صورت تعریف می idempotent ، جابجایی quasigroup: a ∗ b عنصر سوم از سه گانه شامل a و b است. این گروه های چهارگانه همچنین (x ∗ y) ∗ y = x برای همه x و y موجود در چهار گروه را برآورده می کنند. این شبه گروهها به عنوان گروههای چهارگانه اشتاینر شناخته می شوند. ^[۶]
مجموعه {±1, ±i, ±j, ±k} که در آن ii = jj = kk = +1 و با تمام محصولات دیگر مانند گروه چهارگانه ، یک حلقه غیر تعامل نظم را تشکیل می دهد 8. برای استفاده از آن به کوارنیون هایپربولیک مراجعه کنید. (خود کواترنولی هایپربولیک به خودی خود حلقه یا کوزیگروپ را تشکیل نمی دهند).
اكتون هاي غيرفعني با ضرب يك حلقه غير اجتماعي را تشكيل مي دهند. اکتون ها نوع خاصی از حلقه هستند که به حلقه موفانگ معروف است .
یک گروه مشترک شغلی یا خالی است یا گروهی است ، زیرا اگر حداقل یک عنصر وجود داشته باشد ، وجود وارونگی و انجمن گرایی دلالت بر وجود یک هویت دارد.
ساخت زیر مربوط به هانس زاسنهاوس است . در زیر مجموعه فضای بردار چهار بعدی F ⁴ بر روی 3-قسمت Galois F = Z/3Z تعریف کنید

( x ₁ ، x ₂ ، x ₃ ، x ₄ ) ∗ ( y ₁ ، y ₂ ، y ₃ ، y ₄ ) = ( x ₁ ، x ₂ ، x ₃ ، x ₄ ) + ( y ₁ ، y ₂ ، y ₃ ، y ₄ ) + (0 ، 0 ، 0 ، ( x ₃ - y ₃ ) ( x ₁ y ₂ - x ₂ y ₁ )).

سپس، (F⁴, ∗) است جابجایی حلقه Moufang است که یک گروه نیست. ^[۷]

به طور کلی ، مجموعه ای از عناصر nonzero از هر نوع جبر تقسیم بندی یک کوزیگروپ را تشکیل می دهد.

خصوصیات

در ادامه مقاله ، ما باید تکثیر کوآسیگروپ را صرفاً با مخلوط کردن بیان کنیم .

گروه های سهمیه خاصیت فسخ را دارند : اگر ab = ac ، b = c . این از منحصر به فرد بودن تقسیم چپ ab یا ac توسط a است . به همین ترتیب ، اگر ba = ca ، سپس b = c .

اپراتورهای ضرب

تعریف quasigroup را می توان به عنوان شرایط در عملگرهای ضرب در چپ و راست L(x), R(y): Q → Q ، تعریف شده توسط

{\begin{aligned}L(x)y&=xy\\R(x)y&=yx\\\end{aligned}}

تعریف می گوید که هر دو نگاشت می باشد bijections از Q را به خود. ماگما Q دقیقاً زمانی که تمام این اپراتورها برای هر X در Q از لحاظ زیست شناختی یک گروه چهار نفری هستند. نگاشتهای معکوس تقسیمات چپ و راست است ،

{\begin{aligned}L(x)^{-1}y&=x\backslash y\\R(x)^{-1}y&=y/x\end{aligned}}

در این نماد ، هویت در بین عملیات ضرب و تقسیم کوآسیگروپ (بیان شده در بخش جبر جهانی ) است.

{\begin{aligned}L(x)L(x)^{-1}&=1\qquad &{\text{corresponding to}}\qquad x(x\backslash y)&=y\\L(x)^{-1}L(x)&=1\qquad &{\text{corresponding to}}\qquad x\backslash (xy)&=y\\R(x)R(x)^{-1}&=1\qquad &{\text{corresponding to}}\qquad (y/x)x&=y\\R(x)^{-1}R(x)&=1\qquad &{\text{corresponding to}}\qquad (yx)/x&=y\end{aligned}}

که در آن 1 نقشه برداری هویت را در Q نشان می دهد.

مربع های لاتین

The multiplication table of a finite quasigroup is a Latin square: an n × n table filled with n different symbols in such a way that each symbol occurs exactly once in each row and exactly once in each column.

برعکس هر مربع لاتین را می توان به عنوان جدول ضرب یک quasigroup در بسیاری از زمینه ها: مرز ردیف (شامل ستون) و مرز ستون (شامل ردیف سرصفحه) میتواند هر جایگشت از عناصر. دیدن کوچک مربع لاتین و quasigroups.

خصوصیات معکوس

هر عنصر حلقه دارای یک معکوس منحصر به فرد چپ و راست است که توسط آن داده شده است

x^{\lambda }=e/x\qquad x^{\lambda }x=e

x^{\rho }=x\backslash e\qquad xx^{\rho }=e

گفته می شود که اگر یک حلقه وارون ( دو طرفه ) داشته باشد $x^{\lambda }=x^{\rho }$ برای همه x در این حالت عنصر معکوس معمولاً توسط $x^{-1}$ .

چندین مفهوم قوی تر از معکوس در حلقه ها وجود دارد که اغلب مفید هستند:

اگر یک حلقه دارای ویژگی معکوس سمت چپ باشد در صورت وجود $x^{\lambda }(xy)=y$ برای همه $x$ و $y$ . هم ارز، $L(x)^{-1}=L(x^{\lambda })$ یا $x\backslash y=x^{\lambda }y$ .
اگر یک حلقه دارای خاصیت معکوس مناسب باشد در صورت وجود $(yx)x^{\rho }=y$ برای همه $x$ و $y$ . هم ارز، $R(x)^{-1}=R(x^{\rho })$ یا $y/x=yx^{\rho }$ .
اگر یک حلقه خاصیت معکوس ضد اتومورفیک داشته باشد در صورت وجود $(xy)^{\lambda }=y^{\lambda }x^{\lambda }$ یا ، به طور معادل ، اگر $(xy)^{\rho }=y^{\rho }x^{\rho }$ .
وقتی یک حلقه خاصیت معکوس ضعیف را دارد $(xy)z=e$ اگر و تنها اگر $x(yz)=e$ . این ممکن است از نظر وارونگی از طریق بیان شده باشد $(xy)^{\lambda }x=y^{\lambda }$ یا معادل آن $x(yx)^{\rho }=y^{\rho }$ .

یک حلقه دارای خاصیت معکوس اگر آن را تا هر دو سمت چپ و خواص معکوس است. حلقه های خاصیت معکوس همچنین دارای خواص معکوس ضد اتمورفیک و ضعیف هستند. در حقیقت ، هر حلقه ای که از هر چهار هویت فوق را برآورده کند ، خاصیت معکوس را دارد و بنابراین هر چهار را برآورده می کند.

هر حلقه ای که خصوصیات معکوس چپ ، راست یا ضد اتمورفیک را برآورده کند ، بطور خودکار وارونه ای دو طرفه دارد.

مورفيسم

که quasigroup یا حلقه همریخت است نقشه f : Q → P بین دو گروه چهار گانه به گونه ای که f(xy) = f(x)f(y) . همریختی شبه گروه لزوماً تقسیم چپ و راست و همچنین عناصر هویت را حفظ می کند (در صورت وجود).

هموتوپی و ایزوتوپی

بگذارید Q و P چهار گروه باشند. یک هموتوپ quasigroup از Q به P یک نقشه سه گانه (α, β, γ) از Q به P است به گونه ای که

\alpha (x)\beta (y)=\gamma (xy)\,

برای همه x ، y در Q. یک همجنسگرایی quasigroup فقط یک هوموتوپی است که سه نقشه برای آن برابر است.

Isotopy برای هموتوپی که هر یک از سه نقشه (α, β, γ) یک است پوشا و یکبهیک . اگر یک ایزوتوپی بین آنها وجود داشته باشد ، دو كوسیگروپ ایزوتوپی هستند. از نظر مربع های لاتین ، یک ایزوتوپی (α, β, γ) توسط یک ترکیب از ردیف α ، یک مجرا از ستون ها β ، و جایگشتی بر روی عنصر زیر مجموعه γ ، داده می شود.

اتوتوپی نوعی ایزوتوپی است که از یک گروه چهار نفری به خود گرفته می شود. مجموعه ای از تمام autotopies از که quasigroup یک گروه با تشکیل گروه automorphism به عنوان یک زیر گروه.

هر کواریگروپ از نظر حلقه ایزوتوپی است. اگر یک حلقه برای یک گروه ایزوتوپی باشد ، برای آن گروه از نظر هم همورفیک است و بنابراین خود یک گروه است. با این حال ، یک گروه چهار نفری که برای یک گروه ایزوتوپی است ، نیازی به گروه نیست. به عنوان مثال ، كواسيگروپ در R با ضرب داده شده توسط (x + y)/2 براي گروه افزودني (R, +) ايزوتوپيك است ، اما خود گروهي نيست. هر داخلی quasigroup ایزوتوپی به است گروه آبلی توسط قضیه براک-تویودا .

همجوشی (پاراستروفی)

تقسیم چپ و راست نمونه هایی از تشکیل یک گروه چهار نفری با مجاز کردن متغیرها در معادله تعریف است. از عملیات اصلی ∗ (یعنی x ∗ y = z ) می توانیم پنج عملیات جدید تشکیل دهیم: x o y := y ∗ x (عملیات مخالف ) ، / و \ ، و مخالف آنها. این باعث می شود در مجموع شش عملیات شبه گروهی ، که به آن ترکیبات یا parparrophes ∗ می گویند . گفته می شود که هر دو مورد از این عملیات "مزدوج" یا "پاراستروفیک" با یکدیگر (و خودشان) هستند.

ایزوستروف (پاراتوپی)

اگر مجموعه Q دارای دو عملكرد كوسیگروپ ، ∗ و · باشد و یكی از آنها به یك مخلوط دیگر ایزوتوپیك باشد ، گفته می شود كه این عملیات برای همدیگر ایزوستروفیك است . نامهای دیگری نیز برای این رابطه "ایزوستروفی" وجود دارد ، به عنوان مثال ، پاراتوپی .

کلیات

گروه های چند طبقه چند قطبی یا چند لایه

n - ary quasigroup مجموعه ای با عمل <i id="mwAiE">n</i> -ary است ، (Q, f) با f: Qⁿ → Q ، به گونه ای که معادله f(x₁,...,x_n) = y یک راه حل منحصر به فرد دارد برای هر متغیر اگر همه متغیرهای n دیگر به طور دلخواه مشخص شوند. چند پولی یا چند متغیره به معنای n -ary برای تعدادی عدد صحیح غیر عادی n است .

یک گروه شبه صفر یا اصولی ، فقط یک عنصر ثابت Q است . یک گروه چهار نفری یا غیرقابل انکار یک تجرب of Q برای خودش است. گروه کوئری باینری یا دوتایی ، یک گروه چهار قلو معمولی است.

یک مثال از که quasigroup multiary یک عملیات گروه تکرار، y = x₁ · x₂ · ··· · x_n است. لازم نیست از پرانتز برای مشخص کردن ترتیب عملیات استفاده کنید زیرا این گروه ارتباطی است. در صورت مشخص بودن ترتیب عملیات ، می توان با انجام هر دنباله ای از همان گروه یا عملیات گروهی مشابه یا گروه های چهارگانه ، یک گروه چهار قلو تشکیل داد.

گروه های چند طبقه ای وجود دارند که به هیچ وجه نمی توانند نمایان شوند. quasigroup N -ary غیر قابل تقلیل است اگر عملکرد آن را به ترکیب از دو عملیات در راه های زیر نمی توان عامل:

f(x_{1},\dots ,x_{n})=g(x_{1},\dots ,x_{i-1},\,h(x_{i},\dots ,x_{j}),\,x_{j+1},\dots ,x_{n}),

جایی که 1 ≤ i < j ≤ n و (i, j) ≠ (1, n) . quasigroups غیر قابل تقلیل N -ary محدود برای تمام n > 2 وجود دارد؛ برای جزئیات بیشتر به آکیویس و گلدبرگ (2001) مراجعه کنید.

یک شبه گروه nتایی با نسخه N -ary از associativity یک نام گروه n تایی .

شبه گروه های چپ و راست

یک شبه گروه راست (Q, ∗, /) نوعی جبر (2،2) است که هر دو هویت را راضی می کند: y = ( y / x ) ∗ x ؛ y = ( y ∗ x ) / x .

به طور مشابه ، شبه گروه چپ (Q, ∗, \) نوعی جبر (2،2) است که هر دو هویت را راضی می کند: y = x ∗ ( x \ y ). y = x \ ( x ∗ y ).

تعداد شبه گروه های کوچک و حلقه ها

تعداد کلاسهای خودریختی از گروه های کوچک (دنباله A057991 در OEIS) و حلقه ها ((دنباله A057771 در OEIS)) در اینجا آورده شده است: ^[۸]

سفارش	تعداد شبه گروه	تعداد حلقه ها
0	1	0
1	1	1
2	1	1
3	5	1
4	35	2
5	1411	6
6	1،130،531	109
7	12،198،455،835	23،746
8	2،697،818،331،680،661	106،228،849
9	15،224،734،061،438،247،321،497	9،365،022،303،540
10	2،750،892،211،809،150،446،995،735،533،513	20،890،436،195،945،769،617
11	19،464،657،391،668،924،966،791،023،043،937،578،299،025	1،478،157،455،158،044،452،849،321،016

همچنین ببینید

حلقه بول
حلقه تقسیم - حلقه ای که در آن هر عنصر غیر صفر معکوس چند برابر دارد
Semigroup - یک ساختار جبری متشکل از یک مجموعه به همراه یک عملیات دودویی انجمنی
مونوئید - گروهی با عنصر هویت
حلقه سه ضلعی مسطح - دارای یک ساختار حلقه افزودنی و ضرب است
مربع ها و مربع های کوچک لاتین
مشکلات در تئوری حلقه و تئوری کوئیزگروپ
ریاضیات سودوکو

یادداشت

↑ Smith, Jonathan D. H. (2007). An introduction to quasigroups and their representations. Boca Raton, Fla. [u.a.]: Chapman & Hall/CRC. pp. 3, 26–27. ISBN 978-1-58488-537-5.
↑ H. Rubin; J. E. Rubin (1985). Equivalents of the Axiom of Choice, II. Elsevier. p. 109.
↑ (Pflugfelder 1990)
↑ (Bruck 1971)
↑ ^۵٫۰ ^۵٫۱ Damm, H. Michael (2007). "Totally anti-symmetric quasigroups for all orders n≠2,6". Discrete Mathematics. 307 (6): 715–729. doi:10.1016/j.disc.2006.05.033.
↑ (Colbourn و Dinitz 2007)
↑ Smith, Jonathan D. H.; Romanowska, Anna B. (1999), "Example 4.1.3 (Zassenhaus's Commutative Moufang Loop)", Post-modern algebra, Pure and Applied Mathematics, New York: Wiley, p. 93, doi:10.1002/9781118032589, ISBN 978-0-471-12738-3, MR 1673047.
↑ McKay, Brendan D.; Meynert, Alison; Myrvold, Wendy (2007). "Small Latin squares, quasigroups, and loops" (PDF). J. Comb. Des. 15: 98–119. CiteSeerX 10.1.1.151.3043. doi:10.1002/jcd.20105. Zbl 1112.05018.

منابع

Akivis, M. A.; Goldberg, Vladislav V. (2001). "Solution of Belousov's problem". Discussiones Mathematicae. General Algebra and Applications. 21 (1): 93–103. arXiv:math/0010175. doi:10.7151/dmgaa.1030.
Bruck, R.H. (1971) [1958]. A Survey of Binary Systems. Springer-Verlag. ISBN 978-0-387-03497-3.
Chein, O.; Pflugfelder, H. O.; Smith, J.D.H., eds. (1990). Quasigroups and Loops: Theory and Applications. Berlin: Heldermann. ISBN 978-3-88538-008-5.
Colbourn, Charles J.; Dinitz, Jeffrey H. (2007), Handbook of Combinatorial Designs (2nd ed.), Boca Raton: Chapman & Hall/ CRC, ISBN 978-1-58488-506-1
Dudek, W.A.; Glazek, K. (2008). "Around the Hosszu-Gluskin Theorem for n-ary groups". Discrete Math. 308 (21): 4861–76. arXiv:math/0510185. doi:10.1016/j.disc.2007.09.005.
Pflugfelder, H.O. (1990). Quasigroups and Loops: Introduction. Berlin: Heldermann. ISBN 978-3-88538-007-8.
Smith, J.D.H. (2007). An Introduction to Quasigroups and their Representations. Chapman & Hall/CRC Press. ISBN 978-1-58488-537-5.
Shcherbacov, V.A. (2017). Elements of Quasigroup Theory and Applications. Chapman & Hall/CRC Press. ISBN 978-1-4987-2155-4.
Smith, J.D.H.; Romanowska, Anna B. (1999). Post-Modern Algebra. Wiley-Interscience. ISBN 978-0-471-12738-3.

لینک های خارجی

گروه های چهار گانه
Hazewinkel, Michiel ، ed. (2001) [1994]، "شبه گروه" ، دایره المعارف ریاضیات ، اسپرینگر علوم + کسب و کار رسانه BV / Kluwer ناشران علمی، ISBN Hazewinkel, Michiel

[1] Smith, Jonathan D. H. (2007). An introduction to quasigroups and their representations. Boca Raton, Fla. [u.a.]: Chapman & Hall/CRC. pp. 3, 26–27. ISBN 978-1-58488-537-5.

[2] H. Rubin; J. E. Rubin (1985). Equivalents of the Axiom of Choice, II. Elsevier. p. 109.

[3] (Pflugfelder 1990)

[4] (Bruck 1971)

[Damm2007-5] ۵٫۰ ^۵٫۱ Damm, H. Michael (2007). "Totally anti-symmetric quasigroups for all orders n≠2,6". Discrete Mathematics. 307 (6): 715–729. doi:10.1016/j.disc.2006.05.033.

[6] (Colbourn و Dinitz 2007)

[7] Smith, Jonathan D. H.; Romanowska, Anna B. (1999), "Example 4.1.3 (Zassenhaus's Commutative Moufang Loop)", Post-modern algebra, Pure and Applied Mathematics, New York: Wiley, p. 93, doi:10.1002/9781118032589, ISBN 978-0-471-12738-3, MR 1673047.

[8] McKay, Brendan D.; Meynert, Alison; Myrvold, Wendy (2007). "Small Latin squares, quasigroups, and loops" (PDF). J. Comb. Des. 15: 98–119. CiteSeerX 10.1.1.151.3043. doi:10.1002/jcd.20105. Zbl 1112.05018.

α

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]

[۸]