فیلتر تطبیقی
این مقاله نیازمند ویکیسازی است. لطفاً با توجه به راهنمای ویرایش و شیوهنامه، محتوای آن را بهبود بخشید. |
این مقاله به هیچ منبع و مرجعی استناد نمیکند. |
نام دیگر فیلترتطبیقی فیلتر سازگار یا فیلتر وفقی است.
وقتی مطالعه دربارهٔ فیلترهای سازگار را آغاز میکنیم اهمیت زیادی دارد تا نگاهی دقیقتر به مفهوم دو کلمه اصلی فیلتر و سازگار داشته باشیم. صفت سازگار دربارهٔ سیستمهایی بکار میرود که تلاش آنها بر وفق دادن رفتار خود نسبت به محیطی است که در آن قرار دارند. به بیان دیگر سیستمهایی سازگار هستند که میکوشند تا با تغییر مقدار پارامترهای خود عملکردشان را به نحوی متناسب با محیط اطراف خود تنظیم کنند. در این فرایند سیستمی که پارامترهای آن دچار تغییرات شدهاست، فیلتر نام دارد. بر اساس پیچدگی این سیستم یا سرعت عملکرد آن، فیلترهای سازگار گوناگونی وجود دارند که میتوانند عملکردی خطی یا غیر خطی داشته باشند.
کلیترین ساختاری که برای فیلترهای سازگار بکار میرود، ساختار یک فیلتر متقاطع است.
فیلتر سازگار دارای یک سیگنال ورودی و یک سیگنال خروجی است. سیگنالی که علاقه مند هستیم تا خروجی فیلتر مشابه آن تنظیم شود، سیگنال است.
در اینجا دنباله ضرایب، فیلتر است که مقدار دامنه این ضرایب، وزنهای فیلتر نامیده میشود و نیز طول فیلتر میباشد و نیز دنبالهای نمونه برداری شده از سیگنال پیوسته ورودی است که دارای ضریب مطابق با تعداد ضرایب فیلتر است. آنچه در طول این فرایند تغییر میکند، دامنه ضرایب فیلتر یا همان وزنهای فیلتر است که چگونگی تغییر آنها بر اساس الگوریتم فیلتر سازگاری میباشد که برای سیستم خاص تعریف خواهد شد.
بر اساس نظریه وینر هاف، با یک رویکرد احتمالی میتوان تخمین زد که وزنهای بهینه برای فیلتر زمانی بدست میآیند که میانگین مربع خطا به حداقل مقدار خود برسد. در این حالت فیلتر همگرا شدهاست. آنچه در فیلترهای سازگار اهمیت زیادی دارد این است که بتوان الگوریتمی پیاده کرد که با کمترین پیچیدگیهای محاسباتی ریاضی و در حداقل زمان اجرای الگوریتم به مقدار بهینه برسد. زمان اجرای الگوریتم با اندازه گامهای حرکت به سمت نقطه بهینه قابل تنظیم است. اندازه گام کوچک باعث افزایش دقت و کاهش خطا میشود و در عین حال سرعت اجرای الگوریتم را نیز کاهش میدهد. انتخاب اندازه گام بزرگ در حالی که سرعت اجرای الگوریتم را زیاد میکند، به همان نسبت نیز خطای همگرایی را افزایش خواهد داد. پس انتخاب اندازه گام مناسب در فیلترهای سازگار امری بسیار مهم و اساسی است. بر اساس همین نظریه الگوریتم حداقل میانگین مربعات شکل گرفت که مبنای احتمالی و آماری براساس یافتن نقطه بهینه داشته و وزنهای آن بر این اساس تغییر مییابند. الگوریتم حداقل میانگین مربعات، یکی از کلیترین و اساسیترین روشهای اصلاح وزن است که به دلیل سادگی در مفهوم و اجرا کاربرد بسیار زیادی در شاخههای گوناگون دیگر از جمله الگوریتمهای اصلاح وزنها در شبکههای عصبی نیز دارد.
در کنار فواید بیشمار، این الگوریتم دارای معایبی نیز هست که از جمله مهمترین معایب این الگوریتم وابستگی بسیار زیاد رفتار همگرایی الگوریتم به تابع چگالی طیف توان سیگنال ورودی است. اگر ورودی فیلتر سیگنال سفید باشد، به این معنا که سیگنال طیف توان دارای مولفههایی کاملاً مسطح و یکنواخت در تمام فرکانسهای موجود باشد، آنگاه نرخ همگرایی الگوریتم حداقل میانگین مربع بسیار بالا خواهد بود و در غیر این صورت، سرعت همگرایی الگوریتم افت قابل ملاحظهای پیدا خواهد کرد. برای رفع این مشکل الگوریتمهای بسیار زیادی طراحی شد.
در مقابل نظریه وینر هاف که دیدگاهی احتمالی و آماری به اصلاح وزنها دارد، الگوریتمهایی نیز به وجود آمد که با محاسبات دقیق ریاضی نقطه بهینه همگرایی را تعیین میکند. در این الگوریتمها خطای همگرایی بسیار کوچک است و همگرایی الگوریتم با سرعت بسیار بیشتری نسبت به الگوریتمهای مبتنی بر حداقل میانگین مربعات انجام میشود. این افزایش سرعت و دقت در همگرایی در حالی به دست میآید که محاسبات بسیار دقیق و زیاد ریاضی باید در طول همگرایی الگوریتم توسط رایانه انجام شود که سرعت اجرای الگوریتم را به شدت کاهش خواهد داد. به عبارت دیگر افزایش سرعت همگرایی به قیمت افزایش پیچیدگی محاسبات الگوریتم به دست آمدهاست. این الگوریتمها اغلب از معادلات بازگشتی ریاضی استفاده میکنند و در غالب روش کلی الگوریتمهای فیلترهای سازگار حداقل مربعات بازگشتی ارائه شدهاست.
الگوریتم استاندارد حداقل مربعات بازگشتی، یکی از زیر شاخههای این الگوریتم است که از جبر خطی ماتریس معکوس لما استفاده میکند. در نتیجه اجرای این الگوریتم محاسبات پیچیده جبری ماتریسها به همراه تکرارهای زیاد متناسب با طول فیلتر به الگوریتم افزوده خواهند شد.
کاربردهای فیلترهای سازگار[ویرایش]
کاربردهای عملی بسیار زیادی وجود دارد که در آن سیگنالی مطلوب وجود دارد و بر اساس آن سیستم علاقه مند است تا به ازای سیگنال ورودی، سیگنالی را که در خروجی دریافت میکند، مشابه با این سیگنال مطلوب باشد. یکی از مثالهای بارز کاربرد عملی این ساختار، در انتقال اطلاعات است که بهطور گسترده و زیاد از روش جابه جایی متناوب فاز و نیز مدلاسیون مربعی دامنه است که در مخابرات سیار کاربرد بسیار زیادی دارد که در آنها سیگنالها عموماً مختلط هستند و دارای مولفه حقیقی و موهومی میباشند. در حوزه فرکانس نیز سیگنالهای ورودی بیشتر به صورت مختلط هستند که در این حالت در اکثر مواقع فقط بخش حقیقی سیگنال به عنوان سیگنال اصلی در نظر گرفته میشود و از بخش موهومی صرف نظر خواهد شد. با استفاده از این فرض طراحی فیلتر سادهتر شده و از پیچیدگیهای احتمالی محاسبات ناشی از بخش موهومی کاسته میشود. از آنجایی که فیلتر سازگار قادر است خود را با تغییرات محیط تطبیق دهد، میتوان از آن در شاخههای گوناگونی مانند کنترل، مخابرات، پردازش سیگنالهای صوتی و رادار، حذف تداخل، کنترل نویز، مهندسی پزشکی و غیره استفاده کرد. در تمامی این کاربردها وزنهای فیلتر سازگار با توجه به سیگنال مطلوب، در هر بار اجرا، الگوریتم خود را اصلاح کرده و مقادیر متفاوتی را اختیار خواهند کرد. با این دیدگاه میتوان کاربردهای فیلتر سازگار را به چهار دسته کلی تقسیم کرد: شناسایی سیستم، مدل سازی معکوس، پیشگویی خطی، حذف تداخل.
شناسایی سیستم[ویرایش]
در این کاربرد هدف تخمین پارامترهای یک مدل است. بر مبنای دانستههای اولیه از مدل، ابتدا تابع تبدیلی از متغیرهای قابل تنظیم انتخاب میشود. پارامترها در طول الگوریتم تغییر یافته و اصلاح میشوند و در هر بار تغییر با مقدار مطلوب مقایسه میشوند. هرگاه وزنهای جدید پارامترهای منجر به خروجی مطلوب گردد، سیستم به مقدار بهینه خود همگرا شدهاست و به عبارت دیگر تخمین مناسبی از مدل بدست آمدهاست.
در سیستمهای کنترل مدرن، از این شیوه استفاده زیادی شدهاست. یکی از کاربردهای شناسایی سیستم در حذف اکوی صوتی است. در این کاربرد فیلتر سازگار برای شناسایی پاسخ ضربه مسیر بین محل اصلی تولید صدا و جایی که اکو در آن تولید میشود بکار میرود. خروجی فیلتر در این حالت تخمینی از اکوی صوتی است که میتوان با تغییر ضرایب فیلتر آن را تا حد زیادی کاهش داده یا از بین برد. در واقع هدف اصلی پیدایش تعداد زیادی از الگوریتمهایی که در این تحقیق بررسی خواهند شد، در راستای همین کاربرد بودهاست که در بخشهای بعدی با دقت بیشتری به این موضوع خواهیم داشت.
مدل سازی معکوس[ویرایش]
مدل سازی معکوس یا عکس کانولوشن یکی دیگر از کاربردهای فیلترهای سازگار است که در شاخههای متفاوت رشتههای فنی و مهندسی استفاده میشود. یکی از مهمترین کاربردهای آن در مخابرات است که به نام متعادل سازی از آن استفاده میشود. از متعادل سازها برای کاهش اعوجاج کانال استفاده میشود. یکی دیگر از کابردهای مدلسازی معکوس در سیستمهای کنترل است. در طراحی یک کنترلکننده که از به هم بستن تعدادی کنترلکننده تشکیل میشود، تطابق بین هریک از اجزا با یکدیگر و در نتیجه با کل ساختار ضروری است.
پیشبینی خطی[ویرایش]
پیشبینی سیستم یکی دیگر از کاربردهایی فیلترهای سازگار استفاده شدهاست. پیشبینی یکی از روشهای تخیمن طیف سیگنال است که از آن در مدل سازی فرآیندهای تصادفی به منظور یافتن متغیرهای مطرح شده در این طرحها استفاده میشود. در این ترکیب سیگنال از یک فرایند تصادفی توسط فیلتر سازگار با ورودی به وجود آمدهاست. اگر یک فیلتر تمام قطب باشد، آنگاه مدلسازی یک فرایند خود-کاهنده نامیده میشود. ورودی فیلتر بسته به شرایط سیستم میتواند هر سیگنال طبیعی از جمله (نوفه)نویز سفید گاووسی باشد. اگر فیلتر تمام صفر باشد، طرحی دیگری به نام میانگین متحرک شکل میگیرد و در آخر چنانچه فیلتر همزمان دارای تعدادی صفر و قطب باشد، مدل به وجود آمده آرما نام خواهد گرفت. با استفاده از هرکدام از این مدلها و با توجه به نوع پاسخ ضربه کانال که میتواند محدود یا نامحدود باشد، کاربردهای بسیار زیادی مانند ارتقای خط یا رمزکردن سیگنال صحبت به وجود خواهد آمد.
حذف تداخل[ویرایش]
حذف تداخل با توجه به نوع سیگنال مزاحمی که باید حذف شود(نویز/اکوی صوتی/ سیگنالهای مزاحم دیگر)، دارای زیر شاخههای بسیار زیادی است که همگی با کمک فیلترهای سازگار با هدف جدا سازی سیگنال مطلوب از سیگنال مزاحم ایجاد میشوند. در قسمت قبل اشاره شد که برای حذف اکوی صوتی میتوان با مدلسازی اکو، اثر آن را تا حد زیادی از سیگنال صحبت کاهش داد. در این قسمت رویکردی کلی تر و جامع تر از کاربرد فیلترهای سازگار در حذف هر نوع تداخل ارائه میشود. در این روش هدف اصلی در حذف تداخل، بدست آوردن تخمینی از سیگنال مزاحم و کسر آن از سیگنالی است که ترکیبی از پیام اصلی و تداخل است. در واقع حذف تداخل به این روش تنها در صورتی امکانپذیر است مرجع اصلی که تداخل از آن تولید میشود در اختیار باشد. شکل (۱-۴ شمای ساده و کلی از حذف تداخل را نشان میدهد. همانطور که در شکل نشان داده شدهاست در این ساختار دو نوع سیگنال ورودی اولیه و مرجع وجود دارد. سیگنال ورودی اولیه، همان سیگنال مطلوب آغشته به تداخل است و سیگنال مرجع نیز از منبع ایجاد اغتشاش تولید شدهاست. فیلتر سازگار به این منظور بکار میرود تا تخمینی از سیگنال تداخل موجود در سیگنال ورودی اولیه را در خروجی نشان دهد. در آخر هم با کسر خروجی فیلتر یا همان سیگنال تداخل تخمین زده شده از سیگنال ورودی اولیه، سیگنال مطلوب بدست خواهد آمد.
در برقراری ارتباط از طریق خطوط تلفن معمولاً استفاده از یک ترکیب حذفکننده اکو با ساختار شرح داده شده در بالا ضروری است. هنگام انتقال صدا از طریق شبکه ۴ سیم به شبکه ۲ سیم، معمولاً صدای فرد به صورت اکو در طول مسیر برگشت داده میشود که راه حذف این اکوی صوتی با استفاده از فیلترهای سازگار است.
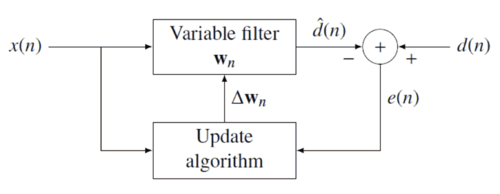
نمودار بلوکی[ویرایش]
نمودار جعبهای که در شکل زیر نشان داده شدهاست، به عنوان یک پایه و اساس خاص فیلتر تطبیقی، مانند حداقل میانگین مربعات (LMS) و حداقل مربعات بازگشتی (RLS) استفاده میشود. اساس این فیلتر استخراج تخمینی از سیگنال مورد نظر است.
برای بحث دربارهٔ نمودار موارد زیر را فرض میکنیم.
- سیگنال ورودی مجموعی از سیگنال مورد نظر و نوفهٔ متداخل است:
- فیلتر متغیر یک ساختار پاسخ ضربهٔ محدود دارد. در چنین ساختاری پاسخ ضره برابر ضرایب فیلتر است. ضرایب یک فیلتر درجه به این صورت تعریف میشوند:
- سیگنال خطا یا تابع هزینه تفاوت بین سیگنال مورد نظر و تخمین زده شدهاست.
فیلتر متغیر سیگنال مورد نظر را با کانوال کردن سیگنال ورودی با پاسخ ضربه تخمین میزند.
که
یک بردار سیگنال ورودی است. فیلتر متغیر ضرایب فیلتر را در هر لحظه تغییر میدهد:
که ضریب تصحیح ضرایب فیلتر است. الگوریتم تطبیقی ضریب تصحیح را بر اساس سیگنال ورودی و خطا میسازد.
منابع[ویرایش]
- Hayes, Monson H. (1996). Statistical Digital Signal Processing and Modeling. Wiley. ISBN 0-471-59431-8.
- Haykin, Simon (2002). Adaptive Filter Theory. Prentice Hall. ISBN 0-13-048434-2.
- Widrow, Bernard; Stearns, Samuel D. (1985). Adaptive Signal Processing. Englewood Cliffs, NJ: Prentice Hall. ISBN 0-13-004029-0.





![{\displaystyle \mathbf {w} _{n}=\left[w_{n}(0),\,w_{n}(1),\,...,\,w_{n}(p)\right]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e685d5a17684150a848ba6c1cf331a88c751f0d1)


![{\displaystyle \mathbf {x} (n)=\left[x(n),\,x(n-1),\,...,\,x(n-p)\right]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/503fcd0731591900ecbc0443d121d4329ae6c813)

