نظریه تجدید

نظریه تجدید شاخه‌ای از نظریه احتمال است که فرایندهای پواسون را به زمان‌های نگهداری اختیاری عمومیت می‌دهد. کاربردهایی شامل محاسبه زمان انتظار برای میمونی که به صورت تصادفی به صفحه کلید ضربه می‌زند تا کلمه مک بت را تایپ کند و به محاسبه مزایای دراز مدت از سیاست‌های تضمینی مختلف بپردازد.

مقدمه

فرایند تجدید، تعمیم یافتهٔ فرایند پواسون است. فرایند پواسون ذاتاً یک فرایند پیوسته مارکوف می‌باشد که توزیع مستقل یکسان از زمانهای نگهداری شده از هر عدد صحیح $i$ با توزیع نمایی قبل از رسیدن به عدد صحیح بعدی $i+1$ با احتمال یک است. در رویه غیررسمی ممکن است نظریه تجدید را به همین صورت تعریف کنیم به جز اینکه زمان‌های نگهداری شده از توزیع عمومی تری گرفته شده‌اند.(توجه داشته باشید که مشخصات توزیع‌های مستقل ویکسان(متغیرهای تصادفی مستقل با توزیع یکسان)از زمان‌های نگهداری شده حفظ می‌شوند.

تعریف ریاضی

Sample evolution of a renewal process with holding times S_i and jump times J_n.

فرض کنید $S_1 , S_2 , S_3 , S_4 , S_5, \ldots$ دنباله‌ای از متغیرهای تصادفی مستقل وتوزیع شده یکسان باشد مثل:$0 <\mathbb{E}[S_i] <\infty.$ فرض می‌کنیم متغیر تصادفی $S_i$ به عنوان $i$امین زمان ثبت شده باشد که برای هر ۰<"n" به صورت زیر تعریف می‌کنیم

$J_n = \sum_{i=1}^n S_i,$

هر$J_n$مربوط به $n$امین پرش زمانی است وبازه$[J_n,J_{n+1}]$ به عنوان بازهٔ تجدید شناخته می‌شود پس متغیر تصادفی $(X_t)_{t\geq0}$ به صورت زیر داده می‌شود. $X_t = \sum^{\infty}_{n=1} \mathbb{I}_{\{J_n \leq t\}}=\sup \left\{\, n: J_n \leq t\, \right\}$ به طوری که $\mathbb{I}$ تابع شاخص مطرح است بیان کننده تعداد پرش است که در زمان t رخ داده است و به عنوان فرایند تجدید خوانده می‌شود.

شرح و تفسیر

ممکن است شخصی فکر کند زمانهای نگهداری شده $\{ S_i: i\geq 1 \}$ به عنوان زمان طی شده قبل از یک خرابی ماشین را در $i$مین بار، در زمان آخرین خرابی باشد. به این فرض توجه کنید که ممکن است ماشین فوراً درست شده باشدوما کلاک را فوراً ریست می‌کنیم). در این تفسیر زمانهای پرش$\{ J_n: n \geq 1 \}$، زمان‌های موفقیت را ثبت می‌کنند که در کد یک از آنها ماشین خراب شده و فرایند تجدید $X_t$، تعداد زمانهایی که تا این جا در زمان داده شده $t$ باید تعمیر شده باشد را ثبت می‌کند. اگر چه این مطلب برای فهم فرایند تجدید با وجود شکل مختصر خود، موثر است چون ممکن است برای مدل کردن تعداد زیادی از موقعیت‌های عملی وابسته استفاده شود ارتباط خیلی نزدیکی با عملکرد ماشین نداشته باشد.

فرایندهای تجدید-پاداش

Sample evolution of a renewal-reward process with holding times S_i، jump times J_n and rewards W_i

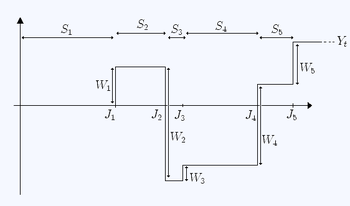
فرض کنید $W_1, W_2, \ldots$ دنباله‌ای از متغیرهای تصادفی (پاداش)،IID باشد که در رابطه $\mathbb{E}|W_i| <\infty. \,$ صدق کند. سپس به متغییر تصادفی $Y_t = \sum_{i=1}^{X_t}W_i$، فرایند تجدید-پاداش گفته می‌شود. توجه کنید که بر خلاف $S_i$، هر$W_i$ ممکن است مقدار منفی را همانند مقادیر مثبت بگیرد. متغییر تصادفی $Y_t$، به دو دنباله وابسته است: زمانهای نگهداری شده $S_1, S_2, \ldots$ وپاداشهای$W_1, W_2, \ldots$، نیازی نیست که این دو دنباله مستقل از هم باشند. اصولاً$W_i$ تابعی از$S_i$است.

تفسیر

در فهم تفسیر بالا از زمان‌های نگهداری شده، به عنوان زمان بین خرابی‌های متوالی یک ماشین، پاداش های$W_1,W_2,\ldots$ (که در این مورد به عنوان منفی بودن اتفاق افتاده است) به عنوان هزینه تعمیر متوالی و به عنوان نتایج خرابی‌های متوالی می‌باشد، بیان می‌شود. یک مقایسه جایگزین این است که، یک غاز جادویی داشته باشیم که بر روی تخم‌ها در بازه‌های توزیع شده مثل$S_i$ (زمان‌های نگهداری شده) می‌خوابد، بعضی وقت‌ها بر روی تخم‌های طلایی با وزنهای تصادفی می‌خوابد و گاهی اوقات بر روی تخمهای سمی می‌خوابد (باوزن‌های تصادفی) که نیازمند درد معرض دید بودن (هزینه بربودن) می‌باشد. پاداشهای $W_i$، سودها یا ضررهای مالی ناشی از تخمهای متوالی می‌باشد و $Y_t$، مجموع مالی از پاداش‌ها در زمان $t$ را ثبت می‌کند.

مشخصات فرایندهای تجدید و فرایندهای پاداش–تجدید

تابع تجدید را به این صورت تعریف می‌کنیم $m(t) = \mathbb{E}[X_t]. \,$

قضیه اولیه تجدید

تابع تجدید در رابطه زیر صدق می‌کند: $\lim_{t \to \infty} \frac{1}{t}m(t) =1/\mathbb{E}[S_1].$

برهان

در زیر شما متوجه می‌شوید که قانون قوی تعداد زیاد برای فرایندهای تجدید به ما می گویند که $\lim_{t \to \infty} \frac {X_t}{t} =\frac{1}{\mathbb{E}[S_1]}.$ برای اثبات قضیه اولیه تجدید، سخت است که نشان دهیم $\left\{\frac{X_t}{t}; t \geq 0\right\}$ به یک شکل قابل انتگرال گیری هستند. برای انجام این، تعدادی از فرایندهای کوتاه شدهٔ تجدید را در نظر بگیرید که زمان‌های نگهداری شده بوسیله $\overline{S_n} = a \mathbb{I}\{S_n> a\}$تعریف می‌شود که $a$ نقطه‌ای است که $0 <F(a) = p <1$که برای هر فرایند تجدید تا معین، وجود دارد $\overline{X_t}$ یک حد بالایی روی $X_t$ است و تجدیدهای آن فقط در شبکه $\{na; n \in \mathbb{N} \}$ اتفاق می‌افتد. علاوه بر این، تعداد تجدیدها در هر زمان تصاعد هندسی با پارامتر $p$ است، بنابراین داریم: $\begin{align}\overline{X_t} &\leq \sum_{i=1}^{[at]} \mathrm{Geometric}(p) \\ \mathbb{E}\left[\,\overline{X_t}\,\right]^2 &\leq C_1 t + C_2 t^2 \\ P\left(\frac{X_t}{t}> x\right) &\leq \frac{E\left[X_t^2\right]}{t^2x^2} \leq \frac{E\left[\overline{X_t}^2\right]}{t^2x^2} \leq \frac{C}{x^2}. \end{align}$

قضیه پایه‌ای تجدید برای فرایندهای تجدید-پاداش

تابع پاداش را به صورت زیر تعریف کرده‌ایم: $g(t) = \mathbb{E}[Y_t]. \,$ تابع تجدید در رابطه زیر صدق می‌کند: $\lim_{t \to \infty} \frac{1}{t}g(t) =\frac{\mathbb{E}[W_1]}{\mathbb{E}[S_1]}.$

معادله تجدید

تابع تجدید در رابطه زیر صدق می‌کند:$m(t) = F_S(t) + \int_0^t m(t-s) f_S(s)\, ds$ به طوری که $F_S$ تابع توزیع عمومی $S_1$ است و $f_S$ تابع چگالی احتمال متناظر است.

برهان معادله تجدید

ممکن است مجدداً انتظار اولین زمان نگهداری شده را بازگو کنیم: $m(t) = \mathbb{E}[X_t] = \mathbb{E}[\mathbb{E}(X_t \mid S_1)]. \,$ ولی بوسیله مشخصه مارکوف داریم: $\mathbb{E}(X_t \mid S_1=s) = \mathbb{I}_{\{t \geq s\}} \left(1 + \mathbb{E}[X_{t-s}] \right). \,$ بنابراین $\begin{align} m(t) & {} = \mathbb{E}[X_t] \\[12pt] & {} = \mathbb{E}[\mathbb{E}(X_t \mid S_1)] \\[12pt] & {} = \int_0^\infty \mathbb{E}(X_t \mid S_1=s) f_S(s)\, ds \\[12pt] & {} = \int_0^\infty \mathbb{I}_{\{t \geq s\}} \left(1 + \mathbb{E}[X_{t-s}] \right) f_S(s)\, ds \\[12pt] & {} = \int_0^t \left(1 + m(t-s) \right) f_S(s)\, ds \\[12pt] & {} = F_S(t) + \int_0^t m(t-s) f_S(s)\, ds, \end{align}$

مشخصه‌های مجانبی

مشخصه‌های مجانبی $(X_t)_{t\geq0}$ و $(Y_t)_{t\geq0}$ در رابطه زیر صدق می‌کند: (قانون قوی تعداد فراوان برای فرایندهای تجدید)$\lim_{t \to \infty} \frac{1}{t} X_t =\frac{1}{\mathbb{E}S_1}$ $\lim_{t \to \infty} \frac{1}{t} Y_t =\frac{1}{\mathbb{E}S_1} \mathbb{E}W_1$ (قانون قوی تعداد فراوان برای فرایندهای تجدید)

برهان

ابتدا در نظر بگیرید $(X_t)_{t\geq0}$، با تعریفی که ما داریم: $J_{X_t} \leq t \leq J_{X_t+1}$ برای همه $t \geq 0$ داریم $\frac{J_{X_t}}{X_t} \leq \frac{t}{X_t} \leq \frac{J_{X_t+1}}{X_t}$ و همچنین چون $0<\mathbb{E}S_i <\infty$، داریم: $X_t \to \infty$

بررسی قیاس ضد و نقیض

ویژگی عجیب فرایندهای تجدید این است که ما در بعضی از زمان‌های از قبل مشخص شده t صبر می‌کنیم و سپس مشاهده می‌کنیم که بازه تجدید شامل t چه اندازه است، ما باید انتظار داشته باشیم که بزرگتر از سایز بازه میانگین باشد. قیاس ضد و نقیض به صورت ریاضی اینگونه بیان می‌شود: برای هر t>0، بازه تجدید شامل t، به صورت اتفاقی بزرگتر از بازه تجدید اولیه است. که برای همه x>0 و همه t>0: $\mathbb{P}(S_{X_t+1}> x) \geq \mathbb{P}(S_1>x) =1-F_S(x)$ که F_S تابع توزیع عمومی IID از زمان‌های نگهداری شده S_i است.

اصل بر هم نهی

روی هم قرار دادن فرایندهای تجدید مستقل، عموماً یک فرایند تجدید نیست، تابع توزیع عمومی از رخدادهای داخلی زمان در فرایند بر هم نهی به وسیله فرمول زیر داده می‌شود: $>R(t) = \sum_{k=1}^K \frac{\alpha_K}{\sum_{k=1}^K \alpha_K} R_k(t) \prod_{j=1,j\neq k}^{K} \alpha_j \int_t^\infty R_j(u)\text{d}u$ به طوری کهR وCDF رخدادهای داخلی زمان هستند و نرخ ورودی فرایندها Kاست.

منابع

• [[Sir

David Cox (statistician) |Cox, David]] (1970). Renewal Theory. London: Methuen & Co.. pp. 142. ISBN 0-412-20570-X. 

• Doob, J. L. (1948). [http://www.ams.org/journals/tran/1948-063-03/S0002-9947-1948-0025098-8/S0002-9947-1948-0025098-8.pdf "Renewal Theory From the Point of View of the

Theory of Probability"]. Transactions of the American Mathematical Society 63 (3): 422–438. JSTOR 1990567. http://www.ams.org/journals/tran/1948-063-03/S0002-9947-1948-0025098-8/S0002-9947-1948-0025098-8.pdf. 

• Smith, Walter L. (1958). "Renewal Theory and Its Ramifications". Journal of the Royal Statistical Society, Series B

(Methodological) 20 (2): 243–302. JSTOR 2983891.