فیلتر منطبق

در پردازش سیگنال، یک فیلتر منطبق (Matched filter)، با هم‌بسته کردن (Correlating) یک سیگنال تأخیرداده‌شدۀ مشخص، یا یک الگو، با یک سیگنال نامعلوم، و با هدف تشخیص آن الگو در سیگنال نامعلوم، پیاده می‌شود. این، معادل هم‌گشتِ (Convolution) سیگنالِ ناشناخته و نسخۀ زمان‌معکوسِ (time-reversed) مزدوجِ مختلط الگوست. فیلتر منطبق، فیلتر خطی بهینه برای بیشینه کردن نسبت سیگنال به نویز (SNR) در حضور نویز سفیدِ جمع‌شونده است.

فیلتر منطبق در رادار استفاده می‌شود، که در آن، سیگنال مشخصی گسیل می‌شود و سیگنال منعکس‌شده (دریافت‌شده) برای یافتن ویژگی‌های مشترک با سیگنال گسیل‌شده بررسی می‌شود. فشرده‌سازی پالس نمونه‌ای از کاربرد فیلتر منطبق در رادار است. در واقع پاسخ ضربه فیلتر گیرنده و سیگنال پالسی گسیل‌شده منطبق هستند.

کاربرد گستردۀ دیگر فیلتر منطبق، در گیرنده‌های مخابراتی دیجیتال است.

فیلتر منطبق دوبعدی معمولاً در پردازش تصویر استفاده می‌شود، برای نمونه، در بهبود SNR مشاهدات اشعه ایکس.

فیلتر منطبق، یک روش دمدولاسیون با فیلترهای زمان‌نامتغیرِ خطی (Linear time-invariant, LTI) برای بیشینه کردن نسبتِ سیگنال به نویز (SNR) نیز هست. این فیلتر، در آغاز، فیلتر نورث نیز نامیده می‌شد.

به‌دست آوردن

به‌دست آوردن از راه جبر ماتریسی

در این بخش، فیلتر منطبق برای یک سیستم زمان‌گسسته به دست می‌آید. روش به دست آوردن آن برای یک سیستم زمان‌پیوسته، مشابه است و جمع‌ با انتگرال جایگزین می‌شود.

فیلتر منطبق، فیلتری خطی است، $h$، که نسبت سیگنال خروجی به نویز را بیشینه می‌کند.

$\ y[n]=\sum _{k=-\infty }^{\infty }h[n-k]x[k],$

که $x[k]$ ورودی، و تابعی از متغیر مستقل $k$، است، و $y[n]$ خروجی فیلترشده است. اگرچه اغلب، فیلترها را به‌عنوان پاسخ ضربۀ سیستم‌های هم‌گشت (Convolution) بیان می‌کنیم، همان‌طور که در بالا می‌بینیم (نظریه سیستم LTI را هم ببینید)، در نظر گرفتن فیلتر منطبق به‌عنوان ضرب داخلی بُرداری (ماتریس یک‌بعدی)، ساده‌تر است.

از سوی دیگر، می‌توان این فیلتر خطی را ازین دیدگاه هم در نظر گرفت که نسبت سیگنال به نویز خروجی را بیشینه کند؛ به‌طور شهودی، فیلتر منطبق بر هم‌بسته کردن سیگنال دریافت‌شده (یک بردار) با فیلتر (یک بردار دیگر) استوار است، به‌گونه‌ای‌که ضرب داخلی این دو بردار بیشینه شود. این کار، توان سیگنال خروجی فیلتر را بیشینه می کند. اگر نویز تصادفی جمع‌شونده را هم در سیگنال دریافت‌شده در نظر بگیریم، با انتخاب فیلتری که بر نویز، متعامد است (تعامد دو بردار)، توان نویز خروجی فیلتر، کمینه می‌شود؛ بنابراین، نسبت سیگنال به نویز، بیشینه می‌شود.

پس به دنبال فیلتر $h$ هستیم، که نسبت سیگنال خروجی به نویز را بیشینه کند، و خروجی فیلتر، حاصل‌ضرب داخلی $h$ و سیگنال ورودی‌ $x$ است.

$x$ از سیگنال مطلوب $s$ و نویز جمع‌شونده $v$ تشکیل شده‌است:

$\ x=s+v.\,$

ماتریس خودهمبستگی نویز - که ماتریسی دارای تقارن هرمیتی است - چنین است:

$\ R_{v}=E\{vv^{\mathrm {H} }\}\,$

که $v^{\mathrm {H} }$، ترانهاد مزدوج $v$ است، و $E$ امید ریاضی (میانگین) است. اگر میانگین $v$ صفر باشد، ماتریس خودهمبستگی آن $R_{v}$ برابر با ماتریس کوواریانس آن است.

$y$، حاصل‌ضرب داخلی فیلتر و سیگنال مشاهده‌شده است:

$\ y=\sum _{k=-\infty }^{\infty }h^{*}[k]x[k]=h^{\mathrm {H} }x=h^{\mathrm {H} }s+h^{\mathrm {H} }v=y_{s}+y_{v}.$

نسبت سیگنال به نویز را به‌عنوان نسبت توان سیگنال مورد نظر خروجی به توان نویز خروجی تعریف می‌کنیم:

$\mathrm {SNR} ={\frac {|y_{s}|^{2}}{E\{|y_{v}|^{2}\}}}.$

و آن را چنین بازمی‌نویسیم:

$\mathrm {SNR} ={\frac {|h^{\mathrm {H} }s|^{2}}{E\{|h^{\mathrm {H} }v|^{2}\}}}.$

می‌خواهیم با انتخاب $h$، این مقدار را بیشینه کنیم. مخرج تابع هدف را چنین می‌نویسیم:

$\ E\{|h^{\mathrm {H} }v|^{2}\}=E\{(h^{\mathrm {H} }v){(h^{\mathrm {H} }v)}^{\mathrm {H} }\}=h^{\mathrm {H} }E\{vv^{\mathrm {H} }\}h=h^{\mathrm {H} }R_{v}h.\,$

حالا، $\mathrm {SNR}$ چنین می‌شود:

$\mathrm {SNR} ={\frac {|h^{\mathrm {H} }s|^{2}}{h^{\mathrm {H} }R_{v}h}}.$

که آن را با دست‌کاری ماتریسی، چنین بازمی‌نویسیم؛ با بهره‌گیری از تقارن هرمیتیِ ماتریس خودهمبستگی $R_{v}$، می‌توان نوشت:

$\mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}},$

یک کران بالا برای این عبارت پیدا می‌کنیم؛ با توجه به نابرابری کوشی-شوارتز:

$\ |a^{\mathrm {H} }b|^{2}\leq (a^{\mathrm {H} }a)(b^{\mathrm {H} }b),\,$

که یعنی مجذور حاصل‌ضرب داخلی دو بردار، حداکثر می‌تواند به اندازه حاصل‌ضرب تک‌تک بردارهای داخلی باشد. کران بالا وقتی به دست می‌آید که دو بردار $a$ و $b$ موازی باشند.

$\mathrm {SNR}$ با توجه به این نابرابری:

$\mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}\leq {\frac {\left[{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)\right]\left[{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)\right]}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}.$

این کران بالا را می‌توان ساده کرد:

$\mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}\leq s^{\mathrm {H} }R_{v}^{-1}s.$

وقتی به این کران بالا می‌رسیم که:

$\ R_{v}^{1/2}h=\alpha R_{v}^{-1/2}s$

که $\alpha$ یک عدد حقیقی دلخواه است. برای تأیید این، آن را در عبارت $\mathrm {SNR}$ که پیش‌تر به‌دست آورده بودیم می‌گذاریم:

$\mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}={\frac {\alpha ^{2}|{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{\alpha ^{2}{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)}}={\frac {|s^{\mathrm {H} }R_{v}^{-1}s|^{2}}{s^{\mathrm {H} }R_{v}^{-1}s}}=s^{\mathrm {H} }R_{v}^{-1}s.$

بنابراین، فیلتر منطبق بهینه چنین است:

$\ h=\alpha R_{v}^{-1}s.$

اغلب، در اثر نویز، متوسط توان خروجی فیلتر را به 1 نرمال می‌کنیم. یعنی:

$\ E\{|y_{v}|^{2}\}=1.\,$

این قید، بر اندازه‌ای از $\alpha$ دلالت می‌کند که:

$\ E\{|y_{v}|^{2}\}=\alpha ^{2}s^{\mathrm {H} }R_{v}^{-1}s=1,$

بنابراین:

$\ \alpha ={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}},$

و فیلتر h نرمال‌شده، چنین به‌دست می‌آید،

$\ h={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}}R_{v}^{-1}s.$

اگر بخواهیم پاسخ ضربه $h$ فیلتر را برپایه سیستم کانولوشن بیان کنیم، $h$ صرفاً مزدوج مختلطِ زمان‌معکوسِ ورودیِ $s$ است.

اگرچه فیلتر منطبق را برای سیستم زمان‌گسسته به‌دست آوردیم، با چند جایگزینی می‌توانیم آن را به سیستم‌ زمان‌پیوسته تعمیم دهیم؛ با فرض سیگنال $s(t)$ ، نویز $v(t)$ و فیلتر $h(t)$، $R_{v}$ را با تابع خودهمبستگیِ زمان‌پیوستۀ نویز، جایگزین می‌کنیم.

به‌دست آوردن از راه ضرائب لاگرانژ

می‌توان فیلتر منطبق را با حل مسئله بیشینه‌سازی از راه ضرائب لاگرانژ هم به‌دست آورد. فیلتر منطبق تلاش می‌کند تا نسبت سیگنال به نویز خروجی ($\mathrm {SNR}$) یک سیگنال معیّن فیلترشده - که نویز تصادفی جمع‌شونده، آن را آلوده - را بیشینه کند. داریم:

$\ x=s+v,\,$

ماتریس خودهمبستگی نویز:

$\ R_{v}=E\{vv^{\mathrm {H} }\}.\,$

نسبت سیگنال به نویز چنین می‌شود:

$\mathrm {SNR} ={\frac {|y_{s}|^{2}}{E\{|y_{v}|^{2}\}}},$

که $y_{s}=h^{\mathrm {H} }s$ و $y_{v}=h^{\mathrm {H} }v$ .

برای صورت، داریم:

$\ |y_{s}|^{2}={y_{s}}^{\mathrm {H} }y_{s}=h^{\mathrm {H} }ss^{\mathrm {H} }h.\,$

و در مخرج،

$\ E\{|y_{v}|^{2}\}=E\{{y_{v}}^{\mathrm {H} }y_{v}\}=E\{h^{\mathrm {H} }vv^{\mathrm {H} }h\}=h^{\mathrm {H} }R_{v}h.\,$

نسبت سیگنال به نویز چنین می‌شود

$\mathrm {SNR} ={\frac {h^{\mathrm {H} }ss^{\mathrm {H} }h}{h^{\mathrm {H} }R_{v}h}}.$

اگر مخرج را به 1 محدود کنیم، مسئله بیشینه کردن $\mathrm {SNR}$، به بیشینه کردن صورت، ساده می‌شود. سپس می توانیم با استفاده از ضریب لاگرانژ مسئله را چنین بنویسیم:

$\ h^{\mathrm {H} }R_{v}h=1$

$\ {\mathcal {L}}=h^{\mathrm {H} }ss^{\mathrm {H} }h+\lambda (1-h^{\mathrm {H} }R_{v}h)$

$\ \nabla _{h^{*}}{\mathcal {L}}=ss^{\mathrm {H} }h-\lambda R_{v}h=0$

$\ (ss^{\mathrm {H} })h=\lambda R_{v}h$

که یک مسئله مقدارِ ویژه تعمیم‌یافته (generalized eigenvalue problem) است:

$\ h^{\mathrm {H} }(ss^{\mathrm {H} })h=\lambda h^{\mathrm {H} }R_{v}h.$

ازآنجاکه رتبۀ (rank) $ss^{\mathrm {H} }$، 1 است، تنها یک مقدار ویژه ناصفر دارد. می‌توان نشان داد که این مقدار ویژه برابر است با:

$\ \lambda _{\max }=s^{\mathrm {H} }R_{v}^{-1}s,$

پس فیلتر منطبق بهینه چنین است:

$\ h={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}}R_{v}^{-1}s.$

این همان نتیجه‌ای است که در بخش پیشین به‌دست آمد.

تفسیر به‌عنوان برآوردگر حداقل مربعات

به‌دست آوردن

فیلتر کردن منطبق را می‌توان یک برآوردگر حداقل مربعات برای مکان و مقیاس‌ بهینه یک مدل معین تفسیر کرد:

$\ x_{k}=s_{k}+v_{k},\,$

که $v_{k}$ نویز ناهم‌بسته با میانگین صفر است. فرض شود که سیگنال $s_{k}$ که یک نسخه مقیاس‌شده و شیفت‌یافتۀ یک دنبالۀ دانستۀ $f_{k}$ باشد:

$\ s_{k}=\mu _{0}\cdot f_{k-j_{0}}$

می‌خواهیم برآوردهای بهینۀ $j^{*}$ و $\mu ^{*}$ شیفتِ نامعلومِ $j_{0}$ و ضریبِ $\mu _{0}$ را با کمینه کردن حداقل مربعات اختلاف دنباله مشاهده‌شده $x_{k}$ و $h_{j-k}$ به دست آوریم:

$\ j^{*},\mu ^{*}=\arg \min _{j,\mu }\sum _{k}\left(x_{k}-\mu \cdot h_{j-k}\right)^{2}$

خواهیم دید که $h_{j-k}$ مناسب، فیلتر منطبق است. داریم:

$\ j^{*},\mu ^{*}=\arg \min _{j,\mu }\left[\sum _{k}(s_{k}+v_{k})^{2}+\mu ^{2}\sum _{k}h_{j-k}^{2}-2\mu \sum _{k}s_{k}h_{j-k}-2\mu \sum _{k}v_{k}h_{j-k}\right].$

جمله اول در براکت‌ها، ثابت است، زیرا سیگنال مشاهده‌شده، در دست است و هیچ اثری روی راه‌حل بهینه ندارد. امید ریاضی جمله آخر هم ثابت است، زیرا نویز، ناهمبسته (uncorrelated) و میانگین آن صفر است. بنابراین می‌توانیم هر دو عبارت را از بهینه‌سازی کنار بگذاریم. پس‌از معکوس‌کردن علامت، مسئله بهینه‌سازی معادل، چنین می‌شود:

$\ j^{*},\mu ^{*}=\arg \max _{j,\mu }\left[2\mu \sum _{k}s_{k}h_{j-k}-\mu ^{2}\sum _{k}h_{j-k}^{2}\right].$

با صفر کردن مشتقِ نسبت به $\mu$، یک پاسخ تحلیلی برای $\mu ^{*}$ چنین می‌شود:

$\ \mu ^{*}={\frac {\sum _{k}s_{k}h_{j-k}}{\sum _{k}h_{j-k}^{2}}}.$

با گذاشتن این در تابع هدف، به یک مسئله بیشینه‌سازی - تنها بر حسب$j^{*}$ - ساده می‌شود:

$\ j^{*}=\arg \max _{j}{\frac {\left(\sum _{k}s_{k}h_{j-k}\right)^{2}}{\sum _{k}h_{j-k}^{2}}}.$

صورت را می‌توان با استفاده از نابرابری کوشی-شوارتز، بالاکران‌دار (upper bounded) کرد:

$\ {\frac {\left(\sum _{k}s_{k}h_{j-k}\right)^{2}}{\sum _{k}h_{j-k}^{2}}}\leq {\frac {\sum _{k}s_{k}^{2}\cdot \sum _{k}h_{j-k}^{2}}{\sum _{k}h_{j-k}^{2}}}=\sum _{k}s_{k}^{2}={\text{constant}}.$

مسئله بهینه‌سازی، وقتی برابری در این عبارت برقرار باشد، به بیشینۀ موردنظر دست می‌یابد. با در نظر گرفتن نابرابری کوشی-شوارتز، تنها وقتی چنین می‌شود که:

$\ h_{j-k}=\nu \cdot s_{k}=\kappa \cdot f_{k-j_{0}}.$

برای ثابت‌های دلخواه ناصفر $\nu$ یا $\kappa$، و پاسخ بهینه‌ چنین خواهد بود: $j^{*}=j_{0}$. بنابراین، $h_{j-k}$ باید مضربی از $f_{k-j_{0}}$ باشد. انتخاب دلخواه $\kappa =1$، فیلتر منطبق را چنین به‌دست می‌دهد:

$\ h_{k}=f_{-k}.$

گویی فیلتر، آینۀ سیگنال است. این تضمین می‌کند که عملیات $\sum _{k}x_{k}h_{j-k}$، در واقع هم‌گشتِ (Convolution) دنبالۀ مشاهده‌شدۀ $x_{k}$ و فیلتر منطبق $h_{k}$ باشد. دنبالۀ فیلترشده وقتی بیشینۀ می‌شود که $x_{k}$ تا جای ممکن (با معیار حداقل مربعات) بر $f_{k}$ منطبق شود.

پیامدها

فیلتر منطبق را می‌توان از چندین روش‌ به‌دست آورد، اما به‌عنوان یک مورد ویژه از روش حداقل مربعات، می‌تواند به‌عنوان یک روش برآورد درست‌نمایی بیشینه یک مدل نویزی گاوسی (رنگی) و درست‌نمایی ویتل (Whittle likelihood) مربوط به آن هم تفسیر شود. اگر سیگنال فرستاده‌شده، هیچ پارامتر نامعلومی (مانند زمان رسیدن، دامنه،...) نداشت، آنگاه فیلتر منطبق، برپایه لم نیمن-پیرسون، احتمال خطا را کمینه می‌کرد. اما، ازآنجاکه سیگنال، عموماً با پارامترهای نامعلوم - که در فرآیند فیلتر کردن تخمین زده یا برازش می‌شوند - تعیین می‌شود، فیلتر منطبق، در واقع یک آمارۀ درست‌نمایی بیشینۀ تعمیم‌یافته را شکل می‌دهد. سری زمانی فیلترشده ممکن است به‌عنوان (یا متناسب با) تابع درست‌نمایی (درست‌نماییِ شرطیِ بیشینه، به‌عنوان تابعی از زمان) تفسیر شود. این، براین‌که "احتمال خطا (در مفهوم نیمن و پیرسون؛ یعنی بیشینه کردن احتمال آشکارسازی درست سیگنال به‌ازای یک احتمال هشدار نادرست (false alarm) معین) لزوماً بهینه نیست" دلالت می‌کند. آن‌چه نسبت سیگنال به نویز (SNR) نامیده می‌شود - که بناست با فیلتر منطبق، بیشینه شود - در واقع به ${\sqrt {2\log({\mathcal {L}})}}$ مربوط می‌شود، که ${\mathcal {L}}$ نسبت درست‌نمایی بیشینۀ مشروط است.

فیلتر منطبق، برپایۀ طیف نویز معلوم پیاده می‌شود. اما در واقعیت، طیف نویز از روی داده ها، و تنها تا دقت محدودی، تخمین زده می‌شود. برای یک طیف نامعلوم، فیلتر منطبق به روش تکرار قدرتمندتری، و چه‌بسا با در نظر گرفتن نویز غیرگاوسی تعمیم داده شود.

تفسیر در حوزۀ فرکانس

در حوزه فرکانس، روشن است که فیلتر منطبق، طوری به مؤلفه‌های طیف وزن می‌دهد که نسبت سیگنال به نویز را بیشینه کند؛ یعنی جاهایی که دامنۀ مؤلفه‌های فرکانسی نویز در طیف، نسبتاً کم هستند، به مؤلفه‌های سیگنال وزن بیشتری می‌دهد، و برعکس. بنابراین، یک پاسخ فرکانسی ناصاف (non-flat) دارد، اما این ناصافی در کاربردهایی مانند رادار و مخابرات دیجیتال، که شکل‌موج سیگنال مشخص است و هدف، تشخیص سیگنال در نویز پس‌زمینه است، نگرانی ندارد. از دیدگاه فنی، فیلتر منطبق یک روش حداقل مربعات وزن‌دار برپایۀ داده‌های ناهم‌واریانس حوزۀ فرکانس است، که وزن‌ها باتوجه‌به طیف نویز تعیین می‌شوند (بخش پیشین را ببینید)، یا معادل آن، یک روش کمترین مربعات به داده‌های سفیدشده اعمال می‌شود.

نمونه‌ها

رادار و سونار

فیلتر منطبق، اغلب در آشکارسازی سیگنال به‌کار می‌رود. برای نمونه، فرض کنید که می‌خواهیم فاصله یک جسم را از راه بازتاب سیگنال از آن به‌دست آوریم؛ یک پالس سینوسی خالص 1 هرتزی به‌سوی جسم گسیل می‌کنیم. فرض می‌کنیم که سیگنال بازتابیده از جسم، نسخه‌ای ضعیف‌شده و تغییرفازیافته از سیگنال گسیل‌شده در کنار نویز جمع‌شونده باشد.

برای یافتن فاصله جسم، پالس دریافت‌شده را با پاسخ ضربۀ یک فیلتر منطبق، هم‌بسته (correlate) می‌کنیم، که آن هم در حضور نویز سفید ناهم‌بسته، سینوسی خالص 1 هرتزی است. وقتی خروجی فیلتر از آستانه‌ای معین فراتر رود، با احتمال زیاد نتیجه می‌گیریم که سیگنال دریافت‌شده، از جسم بازتابیده است. با در نظر گرفتن سرعت انتشار موج و اختلاف زمان میان لحظۀ گسیل شدن سیگنال و لحظۀ آشکار شدن سیگنال در خروجی فیلتر، فاصله جسم را تخمین می‌زنیم. اگر شکل پالس را به روشی خاص تغییر دهیم، نسبت سیگنال به نویز و دقت تخمین فاصله پس‌از فیلتر کردن را می‌توان بهبود بخشید: این روشی است که فشرده‌سازی پالس نام دارد.

افزون‌براین، فیلتر منطبق را می‌توان در تخمین پارامتر هم به‌کار برد (نظریه تخمین را ببینید). در بازگشت به نمونه پیشین، می‌خواهیم سرعت یک جسم متحرک را تخمین بزنیم؛ برای بهره‌گیری از اثر داپلر، می خواهیم فرکانس سیگنال دریافت‌شده را تخمین بزنیم (رادار داپلر). برای این کار، ممکن است سیگنال دریافت‌شده را با چندین فیلتر منطبق سینوسی در فرکانس‌های مختلف هم‌بسته کنیم. فیلتر منطبق با بیشترین خروجی، به‌ احتمال زیاد، فرکانس سیگنال بازتابیده را نشان می‌دهد و به ما کمک می‌کند تا سرعت شعاعی جسم - یعنی سرعت نسبی به‌سوی ناظر یا دورشونده از آن - را تعیین کنیم. این روش در واقع نسخه‌ای ساده از تبدیل فوریه گسسته (DFT) است. DFT، یک ورودی $N$-تایی مختلط را با $N$ فیلتر منطبق از توابع نمایی مختلط در $N$ فرکانس‌ مختلف، هم‌بسته می‌کند، و یک خروجی $N$-تایی مختلط از دامنه ها و فازهای مؤلفه‌های سینوسی به‌دست می‌دهد.

مخابرات دیجیتال

فیلتر منطبق در مخابرات نیز بسیار کاربرد دارد. در یک سیستم مخابراتی که پیام‌های باینری را از راه یک کانال نویزی، از فرستنده به گیرنده می‌فرستد، می‌توان از فیلتر منطبق برای تشخیص پالس‌های فرستاده‌شده در سیگنال دریافت‌شدۀ آلوده به نویز بهره برد.

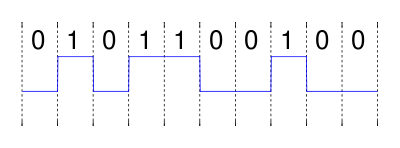
فرض کنید می خواهیم دنباله "0101100100" را به روش ناقطبیِ بی‌بازگشت‌به‌صفر (Nonpolar, non-return-to-zero, NRZ)، و از راه یک کانال مشخص بفرستیم.

از دیدگاه ریاضی، یک دنباله به روش NRZ را می‌توان دنباله‌ای از پالس‌های یکه یا توابع مستطیلی شیفت‌یافته در نظر گرفت. هر پالس، اگر بیت "1" باشد، با 1+، و اگر بیت "0" باشد، با 1- وزن‌دار می‌شود. برای بیت $k$-ام، پالس چنین وزن‌دار می‌شود،

$\ a_{k}={\begin{cases}+1,&{\text{if bit }}k{\text{ is }}1,\\-1,&{\text{if bit }}k{\text{ is }}0.\end{cases}}$

پیام را - به‌عنوان مجموع پالس‌های یکۀ شیفت‌یافته - با $M(t)$ نشان می‌دهیم:

$\ M(t)=\sum _{k=-\infty }^{\infty }a_{k}\times \Pi \left({\frac {t-kT}{T}}\right).$

که $T$ بازۀ یک بیت است و $\Pi (x)$ تابع مستطیلی است.

بنابراین، سیگنال فرستاده‌شده چنین است:

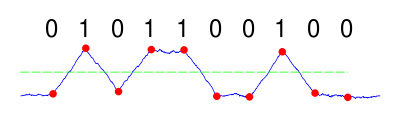
اگر کانال نویزی را با یک کانال AWGN مدل کنیم، نویز گاوسی سفید به سیگنال افزوده می‌شود. سیگنال دریافت‌شده در گیرنده، به‌ازای نسبت سیگنال به نویز 3 دسی‌بل، چنین شکلی دارد:

در نگاه نخست، دنبالۀ فرستاده‌شده در شکل چندان قابل تشخیص نیست. نویزی با توان نسبتا زیاد به سیگنال فرستاده‌شده افزوده شده (نسبت سیگنال به نویز کم است). اگر گیرنده از این سیگنال در لحظه‌های درست نمونه بردارد، پیام باینری حاصل می‌تواند نادرست باشد.

برای افزایش نسبت سیگنال به نویز، سیگنال دریافت‌شده را از یک فیلتر منطبق می‌گذرانیم. در اینجا، فیلتر باید با یک پالس NRZ (معادل "1" در روش NRZ) منطبق باشد؛ پاسخ ضربۀ فیلتر منطبق ایده‌آل - با فرض نویز سفید ناهم‌بسته - باید نسخۀ مقیاس‌شدۀ مزدوج مختلطِ زمان‌معکوسِ سیگنالی باشد که به‌دنبال آن هستیم:

$\ h(t)=\Pi \left({\frac {t}{T}}\right).$

در این حالت، به‌سبب تقارن، مزدوج مختلط زمان‌معکوس $h(t)$، در واقع همان $h(t)$ است. بنابراین پاسخ ضربۀ فیلتر منطبق، همین $h(t)$ است.

پس از هم‌گشت کردن (correlate) سیگنال دریافت‌شده با این فیلتر منطبق، سیگنال حاصل، $M_{\mathrm {filtered} }(t)$، چنین است:

$\ M_{\mathrm {filtered} }(t)=(M*h)(t)$

که $*$ نشان‌دهنده هم‌گشت کردن است.

اکنون می توان از خروجی فیلتر در لحظه‌های نمونه‌برداری درست، با اطمینان نمونه برداشت و با آستانه مناسب مقایسه کرد و در نتیجه دنبالۀ فرستاده‌شده را در گیرنده به‌درستی آشکار کرد.

نجوم امواج گرانشی

فیلتر منطبق در نجوم امواج گرانشی، نقشی بنیادی دارد. نخستین مشاهده امواج گرانشی، با کمک فیلتر کردن مقیاس‌بزرگ خروجی هر آشکارساز برای سیگنال‌های مشابه الگوی موردنظر، و به‌دنبال‌آن غربال‌گری برای محرک‌های هم‌زمان و منسجم میان هر دو ابزار، ممکن شد. نرخ هشدار کاذب، و با آن، اهمیت آماری تشخیص، سپس به‌کمک روش‌های بازنمونه‌گیری ارزیابی شد. استنتاج پارامترهای منبع اخترفیزیکی به‌کمک روش‌های بیزی برپایۀ مدل‌های نظری پارامتری برای شکل موج سیگنال و (دوباره) برپایۀ احتمال ویتل، کامل شد.

یکی دیگر از نمونه‌های پسین کاربرد فیلتر منطبق، تشخیص و تخمین پارامتر امواج گرانشی است.

زیست‌شناسی

جانورانی که در محیط‌های نسبتاً ایستا زندگی می‌کنند، ویژگی‌های نسبتاً ثابتی از محیط را درک می‌کنند. این، تکامل فیلترهایی را فراهم می‌کند که با سیگنال موردنظر با بیشترین نسبت سیگنال به نویز مطابقت دارند؛ یعنی فیلتر منطبق. حسگرهایی که جهان را از راه چنین فیلتر منطبقی درک می‌کنند، اطلاعاتی را که مغز می‌تواند از دنیای بیرون دریافت کند، به‌شدت محدود می‌کند، اما در نهایت، مغز را از محاسبات پیچیده‌تر برای استخراج اطلاعات موردنیاز برای انجام کاری مشخص، بی‌نیاز می‌کند.

همچنین ببینید

• پریودوگرام
• پَس‌اَفکَنِش فیلترشده (تبدیل رادون)
• فیلتر دیجیتال
• پردازش آماری سیگنال
• احتمال ویتل
• تابع درست‌نمایی
• تئوری آشکارسازی سیگنال
• مسئلۀ مقایسه چندگانه
• ظرفیت کانال
• قضیه کدگذاری کانال نویزی
• تخمین چگالی طیف
• فیلتر حداقل میانگین مربعات (LMS).
• فیلتر وینر
• دسته‌بندی چندگانۀ سیگنال (MUSIC)، یک روش فرارزولوشن پارامتریک محبوب
• SAMV

بیشتر بخوانید

• Turin, G. L. (1960). "An introduction to matched filters". IRE Transactions on Information Theory. 6 (3): 311–329. doi:10.1109/TIT.1960.1057571.
•  
• Melvin, W. L. (2004). "A STAP overview". IEEE Aerospace and Electronic Systems Magazine. 19 (1): 19–35. doi:10.1109/MAES.2004.1263229.
• Röver, C. (2011). "Student-t based filter for robust signal detection". Physical Review D. 84 (12): 122004. arXiv:1109.0442. Bibcode:2011PhRvD..84l2004R. doi:10.1103/PhysRevD.84.122004.
• Fish. "Computing the matched filter in linear time". {{cite arxiv}}: |arxiv= required (help)