لایه مرزی استوکس
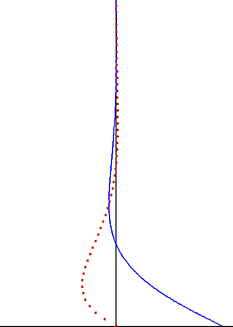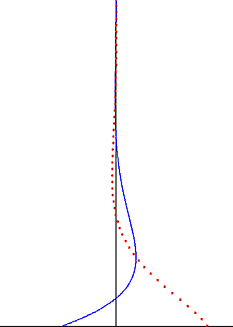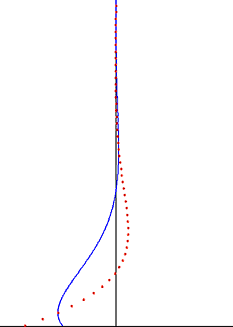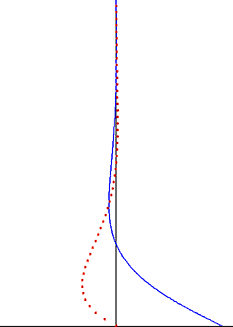
در دینامیک سیالات منظور از لایهٔ مرزی استوکس یا لایهٔ نوسانی استوکس، لایهٔ مرزی نزدیک یک دیوار جامد در جریان نوسانی یک سیال لزج است. همچنین میتواند به لایهٔ مرزی ایجاد شده توسط حرکت نوسانی یک صفحه در سیال لزج ساکن اشاره کند. جرج استوکس یک حل تحلیلی را برای حالتی که جریان آرام و عدد رینولدز پایین باشد، استخراج کرد. این رابطه جزء معدود حلهای دقیق معادلات ناویه-استوکس است.[۱] لایهٔ مرزی استوکس در جریان آشفته نیز وجود دارد، ولی برای محاسبهٔ مشخصات جریان باید از اندازهگیری آزمایشگاهی، شبیهسازی عددی یا روشهای تقریبی استفاده شود.
نوسانهای گردابهای نزدیک مرز[ویرایش]
یک مشاهدهٔ مهم از حل استکوس برای جریان نوسانی استوکس این است که نوسانات گردابهای به یک لایهٔ مرزی نازک و با میرایی نمایی (با دور شدن از دیواره) محدود میشود.[۲] این مشاهده در مورد لایهٔ مرزی آشفته نیز معتبر است. بیرون از لایهٔ مرزی استوکس (که معمولاً بیشتر حجم سیال را شامل میشود) میتوان از نوسانات گردابهای چشمپوشی کرد. با یک تقریب مناسب، نوسانات سرعت جریان در بیرون لایهٔ مرزی، غیرچرخشی هستند و میتوان نظریهٔ جریان پتانسیل را برای بخش نوسانی حرکت به کار برد. این عمل، حل این مسائل را بسیار ساده میکند و برای ناحیههای جریان غیرچرخشی در امواج صوتی و امواج آب به کار میرود.
لایهٔ مرزی استوکس برای جریان آرام در نزدیکی دیواره[ویرایش]
چنین فرض میشود که جریان نوسانی یکبعدی و موازی با دیوارهٔ مسطح باشد. تنها مؤلفهٔ غیر صفر سرعت، u نامیده میشود و در راستای x موازی با جهت نوسان است. افزون بر این، با فرض تراکمناپذیری سیال، مؤلفهٔ سرعت u تنها وابسته به زمان t و فاصله از دیواره z است. همچنین فرض میشود که عدد رینولدز به اندازهٔ کافی کوچک باشد تا جریان آرام باشد. در چنین شرایطی معادلات ناویه-استوکس بدون نیروی خارجی به صورت زیر ساده میشوند:[۳]
که در آن ρ چگالی سیال است که ثابت فرض میشود، p فشار سیال است و ν لزجت سینماتیکی سیال و مقدار آن ثابت است. از آنجایی که u تابعی از موقعیت x نیست، گرادیان فشار ∂p/∂x نیز مستقل از x است. همچنین معادلهٔ ناویه-استوکس برای مؤلفهٔ سرعت عمود بر دیواره به صورت ∂p/∂z = ۰ ساده میشود. در نتیجه فشار و گرادیان فشار، مستقل از فاصله تا دیواره (z) هستند. در نتیجه گرادیان فشار تنها وابسته به زمان است.[۳]
تنها مؤلفهٔ غیر صفر بردار گردابه که ω نامیده میشود، در راستای عمود بر x و zبرابر زیر است:[۲]
با مشتقگیری از معادلهٔ بالا نسبت به z داریم:
نوسان صفحهٔ مسطح صلب[ویرایش]
حرکت هماهنگ صفحهٔ مسطح صلب منجر به کشیده شدن سیال در نزدیکی آن به دلیل تنشهای برشی لزج میشود. فرض کنید که حرکت صفحه به صورت زیر باشد:
که در آن U0 دامنهٔ سرعت صفحه و Ω بسامد زاویهای حرکت است. صفحه که در موقعیت z=۰ قرار دارد، سیال لزج مجاور را به حرکت با سرعت مشابه (u1) وامیدارد که نتیجهٔ آن شرط مرزی بدون لغزش زیر است:
در فاصلهٔ دوری از صفحه (∞ → z) سرعت u1 به صفر میل میکند؛ بنابراین گرادیان فشار در بینهایت برابر صفر است و با توجه به این که تنها وابسته به زمان است و رابطهای با z ندارد، باید در همهجا صفر باشد:[۴]
چنین معادلهای معادلهٔ گرمای یکبعدی یا معادلهٔ انتشار نامیده میشود.
در نتیجه مقدار سرعت جریان به صورت زیر به دست میآید:[۵]
که در آن κ نوعی عدد موج در راستای z و متناظر با طول زیر است:
که ضخامت لایهٔ مرزی استوکس نامیده میشود. در فاصلهٔ δ از صفحه، دامنهٔ سرعت به ۰٫۰۰۲ برابر مقدار U0 در سطح صفحه کاهش مییابد. افزون بر این، نوسانات سرعت به صورت یک موج میرا با طول موج δ و سرعت فاز Ω / κ از دیواره دور میشوند.
پانویس[ویرایش]
- ↑ Wang، C. Y. (۱۹۹۱). «Exact solutions of the steady-state Navier-Stokes equations». Annual Review of Fluid Mechanics. ۲۳: ۱۵۹–۱۷۷. doi:10.1146/annurev.fl.23.010191.001111. بیبکد:1991AnRFM..23..159W.
- ↑ ۲٫۰ ۲٫۱ Phillips (1977), p. 46.
- ↑ ۳٫۰ ۳٫۱ Batchelor (1967), p. 179.
- ↑ Batchelor (1967), p. 190.
- ↑ Batchelor (1967), p. 192.
منابع[ویرایش]
- Batchelor, G.K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. ISBN 0-521-66396-2.
- Lamb, H. (1994). Hydrodynamics (6th ed.). Cambridge University Press. ISBN 978-0-521-45868-9. Originally published in 1879, the 6th extended edition appeared first in 1932.
- Landau, L.D.; Lifshitz, E.M. (1987). Fluid Mechanics. Course of theoretical physics. Vol. 6 (2nd ed.). Pergamon Press. ISBN 0-08-033932-8.
- Phillips, O.M. (1977). The dynamics of the upper ocean (2nd ed.). Cambridge University Press. ISBN 0-521-29801-6.










