مثلثبندی دیلانی

در ریاضیات و هندسهٔ محاسباتی، یک مثلثبندی دیلانی برای یک مجموعه از نقاط به نام P در یک صفحه، یک مثلثبندی به نام (DT(P است به نحوی که هیچ یک از نقاط P درون هیچیک از دایرههای محیطی مثلثهای (DT(P نباشد. این مثلثبندی کمینهٔ زاویههای مثلثها را به بیشترین مقدار ممکن میرساند و به این ترتیب از به وجود آمدن مثلثهای باریک جلوگیری میکند. این مثلثبندی توسط بوریس دیلانی در سال ۱۹۳۴ ابداع شد.[۱] برای چهار یا تعداد بیشتری نقطه روی یک دایره یکسان (به عنوان مثال رأسهای یک مستطیل) تثلیث دیلانی یکتا نیست : هر دو تثلیث ممکن که چهار ضلعی را به دو مثلث تقسیم میکند شرط دیلانی ارضا میکند به عنوان مثال فرض اینکه اگر تمام دایرههای محیطی مثلثها درون تهی باشند. با در نظر گرفتن کرههای محاطی ایدهٔ تثلیث دیلانی به سه یا تعداد بیشتری بعد تعمیم می یابد . تعمیم به سیستم متریک نسبت به سیستم اقلیدسی ترجیح داده میشود ولی در این موارد (اقلیدسی) تثلیث دیلانی الزاماً وجود ندارد یا یکتا نیست.
| در ویکیانبار پروندههایی دربارهٔ مثلثبندی دیلانی موجود است. |
ارتباط با دیاگرام ورونی[ویرایش]
تثلیث دیلانی در فضای گسسته مجموعه p در جنرال پوزیشن مربوط به گرافهای دوگانه از دیاگرام ورونی از مجموعه p. موردهای خاصی که شامل سه نقطهای که روی یک خط اند و چهار نقطهای که روی یک دایرهاند.
-
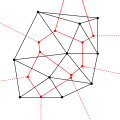
تثلیث دیلانی با تمام دایرههای محیطی و مراکزشان (نقاط قرمز).
-
با وصل کردن مراکزدوایر محیطی میتوان دیاگرام ورونی را تشکیل داد (خطوط قرمز).
دیلانی d بعدی[ویرایش]
دیلانی d بعدی برای مجموع نقاط p در فضای فضای اقلیدسی اقلیدسی d بعدی تثلیث دیلانی( DT( p است بهطوریکه هیچ نقطهای در P درون ابر کره محیطی هر سیمپلکس در (DT(P نباشد . اثبات شده[۲] که در برای هر p یک تثلیث دیلانی یکتا وجود دارد که p گروهی از نقاط در جنرال پوزیشن باشند که نتیجه میدهد هیچ زیر فضای k بعدی آن شامل k + 2 نقطه یا کره k بعدی شامل k + 3 نقطه نباشد برای 1 ≤ k ≤ d − 1 (برای مثال برا ی یک مجموعه نقاط در ℝ3 هیچ سه نقطهای روی یک خط وجود ندارند، هیچ چهار نقطهای روی یک صفحه، هیچ چهار نقطهای روی یک دایره و هیچ 5 نقطهای روی یک کره وجود ندارد) مسئله پیدا کردن تثلیث دیلانی برای گروهی از نقاط در فضای ی بعدی اقلیدسی قابل تبدیل به مسئلهٔ یافتن پوش محدب برای یک مجموعه نقاط در فضای d + 1 بعدی با دادن مختصات اضافی p|2|، به هر نقطه p و گرفتن گوشه پایین پوش محدب و نگاشتن مجدد به فضای d بعدی با حذف مختصات اخیر است. چون پوش محدب یکتاست بنابراین تثلیث نیز یکتاست با فرض اینکه تمام اضلاع پوش محدب سیمپلکس هستند . اضلاع غیر سیمپلکس تنها زمانی پدید می آیند که d + 2 تا از نقاط اصلی روی یک ابر کرهابر کره دی بعدی باشند به عنوان مثال نقاط در جنرال پوزیشن نباشند.
ویژگیها[ویرایش]


فرض کنید n تعداد نقاط و d تعداد بعد باشد.
1- اتحاد تمام سیمپلکسها در تثلیث, پوش محدب تمام نقاط است.
2- تثلیث دیلانی شامل O(n⌈d / 2⌉)
مثلث است.[۳]
3- در صفحه (d =2) اگر b راس در پوش محدب باشند هر تثلیثی از آن نقاط حدااکثر 2n - 2 - b مثلث دارد به علاوه یک وجه بیرونی در صفحه.
4- هر راس حداقل توسط شیش مثلث محاصره شده.
5- در صفحه، تثلیث دیلانی مینمم زاویه را بیشینه میکند در مقایسه با هر تثلیث دیگری ازنقاط کوچکترین زاویه در تثلیث دیلانی حداقل به بزرگی کوچکترین زاویه در بقیه است اما تثلیث دیلانی الزاماً ماکسیمم زاویه را کمینه نمیکند تثلیث دیلانی همچنین الزاماً طول اضلاع را مینمم نمیکند.
6- دایرهای که بر هر مثلث دیلانی محیط است هیچ نقطه داخلی دیگری درون خود ندارد.
7- اگر یک دایره که از دو تا از نقاط داده شده بگذرد هیچ نقطه دیگری درون خود ندارد بنابراین بخشی که دو نقطه را به هم متصل میکند یک ضلع تثلیث دیلانی نقاط داده شدهاست.
8- هر مثلث تثلیث دیلانی برای نقاط فضای d بعدی در یک وجه پوش محدب تصویر نقاط روی سهمی وار d + 1 بعدی صدق میکند و بلعکس.
9- نزدیکترین همسایگی b به هر نقطه p روی یک ضلع در تثلیث دیلانی قرار دارد چون نزدیکترین گراف همسایه یک زیر گراف از تثلیث دیلانی است.
10- تثلیث دیلانی یک اسپنر هندسی است :کوتاهترین مسیر بین دو راس در طول اضلاع دیلانی بیشتر از برابر فاصله اقلیدسی بین آنها نیست.
تعبیر تصویری دیلانی : چرخاندن[ویرایش]
از ویژگیهای فوق یک ویژگی بدست میآید . با نگاه کردن به دومثلث ABD و BCD با ضلع مشترک BD اگر زوایای α و γ کوچکتر مساوی 180 شود مثلثها شرط دیلانی را براورده میکنند. این یک ویژگی بسیار مهم است چون ما را قادر به استفاده از تکنیک چرخاندن میکند . اگر دو مثلث شرط دیلانی را برآورده نکنند جا به جا کردن ضلع مشترک BD با ضلع مشترک AC دو مثلث تولید میکند که شرط دیلانی را براورده میکند.
-
این مثلث بندی دیلانی رانمیسازد چون جمع دو زاویه وربرو بالایی و پایینی بیشتر از 180 است.
-
این مثلث بندی دیلانی نیست چون یک دایره محیطی بیش از سه نقطه در بردارد.
-
چرخاندن ضلع معمول باعث میشود که تثلیث دیلانی تکیل شود.
الگوریتمها[ویرایش]
الگوریتمهای زیادی برای محاسبهٔ تثلیث دیلانی بر اساس عملیات سریع برای یافتن نقطهای درون دایره محیطی مثلث و یک داده ساختار کارامد برای ذخیره سای مثلثها و اضلاع وجود دارد. در دو بعد یک راه برای فهمیدن اینکه آیا نقطه d درون دایره محیطی A و B و C قرار دارد محاسبه دترمینان این ماتریس به ما نشان میدهد.[۴] .
. وقتی A و B و C به ترتیب پاد ساعت گرد مرتب شوند این دترمینان مثبت است اگر و تنها اگر d درون دایره محیطی باشد .
الگوریتم چرخاندن[ویرایش]
همان طور که در بالا ذکر شد اگر یک مثلث غیر دیلانی باشد ما میتوانیم یکی از ضلعهای ان را بچرخانیم کنیم. این منجر به یک الگوریتم راحت میشود : هر تثلیث از نقاط را بسازید و سپس اضلاع را بچرخانید تا زمانی که هیچ مثلثی غیر دیلانی نباشد. متأسفانه این عملیات ازین (O(n2 چرخاندن ضلع لازم دارد و به سه یا بیش از آن قابل تعمیم نیست.[۲].
افزایشی[ویرایش]
آسانترینترین راه برای محاسبه کارامد تثلیث دیلانی افزودن مکرر راس در یک زمان و تثلیث مجدد قسمتهای تغییر یافته گراف است.
وقتی یک راس v اضافه میشود ما مثلث شامل v را به سه قسمت تقسیم میکنیم سپس الگوریتم چرخاندن را اعمال میکنیم اگر اینکار به صورت اشتباه انجام شود از (O(n مرتبه زمان میبرد. ما بین تمام مثلثها جستجو کرده تا v را پیدا کنیم سپس هر مثلث را یکبار میچرخانیم پس زمان اجرا کلی از اردر (O(n2 است .
اگر ما راسهایی به صورت تصادفی وارد کنیم معلوم میشود (با شواهد پیچیده) که هر ورود بهطور متوسط فقط (O(1 مثلث را میچرخاند - با و جود اینکه امکان دارد گاهی اوقات تعداد بیشتری را بچرخاند[۵]. این هنوز زمان یافتن مکان نقطه را قابل بهبود میگذارد . ما میتوانیم تاریخچه تقسیمها و چرخاندنهای انجام شده را ذخیره کنیم: هر مثلث یک اشاره گر به دو یا سه مثلث که جایگزین آن شدهاند را ذخیره میکند . برای یافتن مثلثی که v را در بر دارد ما از مثلث پایه شروع میکنیم و اشارهگری که به مثلث شامل v اشاره میکند را
دنبال میکنیم تا جایی که به مثلثی برسیم که هنوز جایگزین نشدهاست بهطور متوسط این عملیات (O(log n زمان میبرد . برای تمام رأسها این عملیات ازین (O(n logn زمان میبرد[۲] . در حینی که این تکنیک به ابعاد بالاتر تعمیم می یابد (همانطور که توسط ادلزبرونر و شاح ثابت شده[۶]) ) زمان اجرا میتواند نسبت به بعد نمایی رشد کند اگر تثلیث دیلانی نهایی کوچک باشد.
الگوریتم بویر واتسون یک رویکرد ساختار افزایشی دیگر را ارائه میدهد این رویکرد جایگزینی برای ضلع چرخان برای محاسبهٔ مثلثهای دیلانی شامل یک راس تازه وارد شده میباشد.
تبدیل به زیر مسئلهها[ویرایش]
الگوریتم تبدیل به زیر مسئله ها برای تثلیثها در ابعاد دو توسط لیی و شاختر ابداع شد و توسط گی باس و استولفی[۷] بهبود داده شد و بعدها توسط دویر. در این الگوریتم مکرراً خطی برای تقسیم رأسها به دو مجموعه رسم میشود. تثلیث دیلانی برای هر مجموعه محاسبه میشود و سپس دو مجموعه در طول خط تقسیم ترکیب میشوند با استفاده چند شگرد هوشمندانه عملیات ترکیب میتواند در زمان (O(n انجام شود بنابراین زمان اجرا کل این (O(n logn است[۸]
.
برای گونه خاصی مشخصی از مجموعه نقاط از قبیل توزیع یکنواخت تصادفی با انتخاب هوشمند خطوط تقسیم زمان مورده انتظار میتواند به (O(nlog logn کاهش یابد در حالی که هنوز اجرای بدترین حالت را در اختیار دارد.
الگوریتم تبدیل به زیر مسئلهها برای اجرای یک تثلیث در d بعد در قالب "دی وال : یک الگوریتم سریع تقسیم وغلبه تثلیث دیلانی در Ed"" توسط سیگنونی و منتانی و اسکوپینو ارائه شدهاست[۹]
.
تقسیم و غلبه نشان داده که سریعترین تکنیک تولید DT است[۱۰][۱۱].
خط جاروب[ویرایش]
الگوریتم شانس از تکنیک خط جاروب برای رسیدن به زمان اجرا (O(n logn در حالت صفحهای استفاده میکنند.
پوش جاروب[ویرایش]
پوش جاروب[۱۲] یک تکنیک ترکیبی برای تثلیث دیلانی دو بعدی است که از یک جاروب تکثیر شعاعی (به ترتیب به وجود امده از مجموعه نقاط دو بعدی مرتب شده با فرض تثلیث بدون تداخل ) استفاده میکند که با یک قدم چرخاندن مثلث مکرر تزویج شدهاست . همچنین یک متغیر منطقی صحیح دقیق برای الگوریتم ارائه میشود.
کاربردها[ویرایش]

درخت پوشای حداقل اقلیدسی یک مجموعهای از نقطهها زیرمجموعهای از تثلیث دیلانی همان نقاط میباشد و این میتواند در کارایی محاسبات استفاده شود.
تثلیث دیلانی برای مدلسازی زمینه و اشیای دیگر که به عنوان مجموعهای از نقاط داده شدهاند یک مجموعهٔ خوبی از مثلثها را میدهد که میتواند به عنوان چند ضلعی در مدل استفاده شود. بهطور خاص تثلیث دیلانی سعی دارد از مثلثهای باریک استفاده نکند(که آنها درمقایسه با مساحت شان دایره محیطیهای بزرگی دارند). تثلیث دیلانی میتواند برای مشخص کردن چگالی یا شدت نقاط در مدلسازی نقاط به معنی Delaunay tessellation field estimator استفاده شوند. تثلیث دیلانی به دلیل تضمین زاویه و به دلیل الگوریتمهای مثلث بندی سریع توسعه یافته اغلب مورد استفاده برای ایجاد شبکه برای حل فضای گسسته مانند روش المان محدود و روش حجم محدود که از روشهای شبیهسازی فیزیکی قرار میگیرند. بهطور معمول، دامنه شبکه بندی به عنوان یک مجموعه مختلط ساده ی درشت مشخص شدهاست، برای شبکه به صورت عددی پایدار، باید آن خالصسازی کرد. به عنوان مثال با استفاده از الگوریتم راپرت . افزایش محبوبیت استفاده از روش المان محدود و تکنیکهای روش المان مرزی انگیزه برای بهبود الگوریتمهای ی درگیر به صورت خودکار را افزایش میدهد. با این حال، همهٔ این الگوریتمها میتوانند عناصر شبکه نامنظم و حتی غیرقابل استفاده ایجاد کند. خوشبختانه، چندین روش وجود دارد که میتواند یک شبکه بندی موجود را بگیرد و آن را بهبود کیفیت بدهد. به عنوان مثال، صاف کردن ( همچنین به عنوان پالایش شبکه بندی نیز نامیده میشود) یکی از این روش هاست، که انباشتگیهای محل گرهها را به منظور به حداقل رساندن اعوجاج عنصر میباشد . روش شبکه کشیده اجازه میدهد تا نسلی از شبکه شبه منظم که با ضوابط دیلانی سنخیت دارند و راه حلهای یک مرحله ا ی دارند رشد کنند.
منابع[ویرایش]
- ↑ B. Delaunay: Sur la sphère vide, Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk, 7:793–800, 1934
- ↑ ۲٫۰ ۲٫۱ ۲٫۲ de Berg, Mark; Otfried Cheong; Marc van Kreveld; Mark Overmars (2008). Computational Geometry: Algorithms and Applications (PDF). Springer-Verlag. ISBN 978-3-540-77973-5. Archived from the original (PDF) on 28 اكتبر 2009. Retrieved 21 May 2014.
{{cite book}}: Check date values in:|archive-date=(help) - ↑ Seidel, R. (1995). "The upper bound theorem for polytopes: an easy proof of its asymptotic version". Computational Geometry. 5 (2): 115–116. doi:10.1016/0925-7721(95)00013-Y.[پیوند مرده]
- ↑ Guibas, Lenoidas; Stolfi, Jorge (1985-04-01). "Primitives for the manipulation of general subdivisions and the computation of Voronoi". ACM. p. 107. Retrieved 2009-08-01.
- ↑ Guibas, L. (1992). "Randomized incremental construction of Delaunay and Voronoi diagrams". Algorithmica. 7: 381–413. doi:10.1007/BF01758770.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help)[پیوند مرده] - ↑ Edelsbrunner, Herbert; Nimish Shah (1996). "Incremental Topological Flipping Works for Regular Triangulations". Algorithmica. 15 (3): 223–241. doi:10.1007/BF01975867.[پیوند مرده]
- ↑ «Computing Constrained Delaunay Triangulations». بایگانیشده از اصلی در ۲۲ سپتامبر ۲۰۱۷. دریافتشده در ۲۱ مه ۲۰۱۴.
- ↑ Leach, G. (1992). "Improving Worst-Case Optimal Delaunay Triangulation Algorithms.". CiteSeerX: 10.1.1.56.2323.
{{cite journal}}: Cite journal requires|journal=(help); Unknown parameter|month=ignored (help) - ↑ Cignoni, P. (1998). "DeWall: A fast divide and conquer Delaunay triangulation algorithm in Ed". Computer-Aided Design. 30 (5): 333–341. doi:10.1016/S0010-4485(97)00082-1.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ A Comparison of Sequential Delaunay Triangulation Algorithms http://www.cs.berkeley.edu/~jrs/meshpapers/SuDrysdale.pdf
- ↑ http://www.cs.cmu.edu/~quake/tripaper/triangle2.html
- ↑ S-hull
ارجعات بیرونی[ویرایش]
- Delaunay triangulation in CGAL, the Computational Geometry Algorithms Library:
- Yvinec, Mariette. "2D Triangulation". Retrieved April 2010.
{{cite web}}: Check date values in:|accessdate=(help) - Pion, Sylvain; Teillaud, Monique. "3D Triangulations". Retrieved April 2010.
{{cite web}}: Check date values in:|accessdate=(help) - Hert, Susan; Seel, Michael. "dD Convex Hulls and Delaunay Triangulations". Retrieved April 2010.
{{cite web}}: Check date values in:|accessdate=(help)
- Yvinec, Mariette. "2D Triangulation". Retrieved April 2010.
- "Delaunay triangulation". Wolfram MathWorld. Retrieved April 2010.
{{cite web}}: Check date values in:|accessdate=(help) - "Qhull". Retrieved April 2010.
{{cite web}}: Check date values in:|accessdate=(help) — Code for Convex Hull, Delaunay Triangulation, Voronoi Diagram, and Halfspace Intersection - Shewchuk, Jonathan Richard. "Triangle". Retrieved April 2010.
{{cite web}}: Check date values in:|accessdate=(help) – A Two-Dimensional Quality Mesh Generator and Delaunay Triangulator - Kumar, Piyush; Mohanty, Somya. "Triangle++". – A C++ wrapper on Triangle
- "Poly2Tri". Google Code. Retrieved April 2010.
{{cite web}}: Check date values in:|accessdate=(help) – A sweepline Constrained Delaunay Triangulation (CDT) library, available in ActionScript 3, C, C++, C#, Go, Haxe, Java, Javascript, Python and Ruby