نظریه کیرشهف

در حوزهٔ ریاضیات و در موضوع نظریه گراف، نظریهٔ کیرشهف یا نظریهٔ ماتریس درخت کیرشهف که از روی اسم گوستاو کیرشهف نامگذاری شده‌است در مود تعداد درخت‌های پوشا در یک گراف است که نشان می‌دهد این عدد را می‌توان در زمان چند جمله ای به عنوان دترمینان ماتریس به دست آمده از گراف محاسبه کرد. این نظریه یک تعمیم از فرمول کیلی است که تعداد درخت‌های پوشا در یک گراف کامل به دست می‌آورد.

نظریهٔ کیرشهف بر پایهٔ مفهموم ماتریس لاپلاس یک گراف است که برابر با اختلاف بین ماتریس درجه (یک ماتریس قطری با درجهٔ راس‌ها در قطرها) و ماتریس مجاورت آن است.

برای یک گراف همبند مشخص G با n راس نامگذاری شده فرض کنید λ₁, λ₂, … , λ_n₋₁ مقادیر ویژه غیر صفر ماتریس لاپلاس آن باشد. پس تعداد درخت‌های پوشای G برابر است با:

t(G)={\frac {1}{n}}\lambda _{1}\lambda _{2}\cdots \lambda _{n-1}\,.

که یعنی تعداد درخت‌های پوشا برابر با هر هم عامل ماتریس لاپلاس G است.

مثالی از نظریهٔ ماتریس درخت[ویرایش]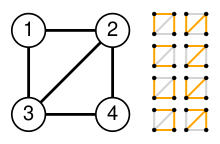

در ابتدا، ماتریس لاپلاس Q را برای گراف الماسی G می‌نویسیم (تصویر را در سمت چپ ببینید):

Q=\left[{\begin{array}{rrrr}2&-1&-1&0\\-1&3&-1&-1\\-1&-1&3&-1\\0&-1&-1&2\end{array}}\right].

سپس، ماتریس ^* Q را با حذف کردن یکی از سطرها و ستون‌های ماتریس Q تشکیل می‌دهیم. برای مثال، با حذف ردیف ۱ و ستون ۱ داریم:

Q^{\ast }=\left[{\begin{array}{rrr}3&-1&-1\\-1&3&-1\\-1&-1&2\end{array}}\right].

در نهایت، دترمینان ^* Q را برای ساخت (t(G به دست می‌آوریم که برای گراف الماسی برابر ۸ است. (توجه کنید که (t(G یک هم عامل (۱٬۱) از Q در این مثال است)

اثبات کلی[ویرایش]

ابتدا در نظر داشته باشید که لاپلاس خاصیتی دارد که مجموع تعداد مقادیرش در هر ستون و در هر ردیف برابر با صفر است. پس می‌توانیم هر کهاد را با افزودن ستون‌ها و ردیف‌ها، جابه‌جا کردن آن‌ها یا ضرب یک ردیف یا ستون در ۱- یه یک کهاد دیگر تبدیل کنیم؛ بنابراین هم عامل‌ها مشابه هم هستند و می‌توان تأیید کرد که در واقع آن‌ها علامت یکسانی دارند.

در ادامه اقدام به نشان دادن این می‌کنیم که دترمینان کهاد M₁₁ تعداد درخت‌های پوشا را می‌شمارد. فرض کنید n تعدا راس‌های گراف و m تعداد یال‌های آن باشد. ماتریس وقوع $E$ یک ماتریس n در m است که به این صورت تعریف می‌شود: فرض کنید که (i,j) یال k -ام گراف باشد، و i <j. پس E_ik = ۱ و E_jk = −۱، و تمام مقادیر ستون k برابر ۰ است. برای مثال قبل (با n = ۴ و m = ۵) داریم:

E={\begin{bmatrix}1&1&0&0&0\\-1&0&1&1&0\\0&-1&-1&0&1\\0&0&0&-1&-1\\\end{bmatrix}}.

در نظر داشته باشید که لاپلاس L می‌تواند به حاصل ضرب ماتریس وقوع و ترانهاده اش ساده شود، یعنی L = EE^T. علاوه بر این، فرض کنید F همان ماتریس E باشد که اولین ردیفش حذف شده باشد، پس داریم FF^T = M₁₁.

حالا فرمول کوچی - بینت اجازه می‌دهد که بنویسیم:

\det(M_{11})=\sum _{S}\det(F_{S})\det(F_{S}^{T})=\sum _{S}\det(F_{S})^{2}

که محدودهٔ S بین زیرمجموعه‌های [m] با اندازهٔ n-1 است و F_S نشان می‌دهد که ماتریس (n − ۱) در (n − ۱) که ستون‌هایش همان F هستند که در S مرتب شده‌اند. پس هر S با n − ۱ یال از گراف اصلی، و می‌توان نشان داد که آن یال‌ها موجب یک درخت پوشا می‌شوند اگر و تنها اگر دترمینان F_S برابر با ۱+ یا ۱- باشد، و موجب یک درخت پوشا نمی‌شوند اگر و تنها اگر دترمینان برابر ۰ شود. اثبات در همین‌جا به پایان می‌رسد.

موارد خاص و تعمیم‌ها[ویرایش]

فرمول کیلی[ویرایش]

فرمول کیلی از نظریهٔ کیرشهف به عنوان یک حالت خاص تبعیت می‌کند چون هر بردار با طول ۱ در هر مکان، ۱- در مکان دیگر و ۰ در جایی دیگر یک بردار ویژه از ماتریس لاپلاس گراف کامل با مقدار ویژهٔ متناظر با n است. این بردارها با هم دیگر یک فضا به اندازهٔ n − ۱ پوشش می‌دهند که پس هیچ مقدار ویژهٔ غیرصفر دیگری وجود ندارد.

متناوباً، توجه داشته باشید که همان‌طور که فرمول کیلی تعداد درخت‌های نامگذاری شدهٔ مجزای یک گراف کامل K_n را به دست می‌آورد، ما باید هر هم عامل ماتریس لاپلاس K_n را محاسبه کنیم. لاپلاس ماتریس در این مورد برابر است با:

{\begin{bmatrix}n-1&-1&\cdots &-1\\-1&n-1&\cdots &-1\\\vdots &\vdots &\ddots &\vdots \\-1&-1&\cdots &n-1\\\end{bmatrix}}.

هر هم عامل از ماتریس بالا برابر است با nⁿ⁻². که همان فرمول کیلی است.

نظریهٔ کیرشهف برای گراف‌های چندگانه[ویرایش]

نظریهٔ کیرشهف برای گراف‌های چندگانه نیز به خوبی صادق است؛ ماتریس Q به صورت زیر اصلاح شده‌است:

مقدار q_i,j برابر با m- است. که m تعداد یال‌های بین i و j است؛
هنگام شمردن درجهٔ یک راس، تمام دورها حذف می‌شوند.

فرمول کیلی برای یک گراف چندگانهٔ کامل برابر با (m^n-1(n^n-1-(n-1)n^n-2 است که از روش بالا ساخته شده‌است چون یک گراف ساده یه گراف چندگانه با m = ۱ است.

همچنین بخوانید[ویرایش]

منابع[ویرایش]

Harris, John M.; Hirst, Jeffry L.; Mossinghoff, Michael J. (2008), Combinatorics and Graph Theory, Undergraduate Texts in Mathematics (2nd ed.), Springer.
Maurer, Stephen B. (1976), "Matrix generalizations of some theorems on trees, cycles and cocycles in graphs", SIAM Journal on Applied Mathematics, 30 (1): 143–148, doi:10.1137/0130017, MR 0392635.
Tutte, W. T. (2001), Graph Theory, Cambridge University Press, p. 138, ISBN 978-0-521-79489-3.
Chaiken, S.; Kleitman, D. (1978), "Matrix Tree Theorems", Journal of Combinatorial Theory, Series A, 24 (3): 377–381, doi:10.1016/0097-3165(78)90067-5, ISSN 0097-3165

پیوند به بیرون[ویرایش]