ناهماهنگی

در مکانیک کلاسیک، ناهماهنگی (به انگلیسی: anharmonicity) یا ناهارمونیکی عبارت است از انحراف یک سامانه از داشتن یک نوسان‌سازی هماهنگ. نوسان‌سازی که در حرکت هماهنگی نوسانی ندارد به عنوان نوسانگر ناهماهنگ شناخته می‌شود که در آن سامانه را می‌توان به یک نوسانگر هماهنگ تقریب‌زد و ناهماهنگی را می‌توان با استفاده از نظریه پریشیدگی محاسبه کرد. اگر ناهماهنگی زیاد باشد، باید از فنون‌های عددی دیگری استفاده کرد. در واقع تمام سامانه‌های نوسانی ناهماهنگ هستند، اما بیشتر آنها که دامنه نوسان کمتر است به نوسانگر هماهنگ نزدیک می‌شوند.

در نتیجه نوسانات با فرکانس‌ها $2\omega$ و $3\omega$ و غیره، که $\omega$ فرکانس اساسی نوسانگر است، ظاهر می‌شود. علاوه بر این، فرکانس $\omega$ از فرکانس $\omega _{0}$ از نوسانات هماهنگ منحرف می‌شود همچنین رجوع کنید به میان‌مدگرایی و تُن‌های ترکیبی. به عنوان اولین تقریب، جابجایی فرکانس $\Delta \omega =\omega -\omega _{0}$ متناسب با مجذور دامنه نوسان $A$ است:

\Delta \omega \propto A^{2}

در سامانه‌ای از نوسانگرها با فرکانس‌های طبیعی $\omega _{\alpha }$ ، $\omega _{\beta }$ ،... ناهماهنگی منجر به نوسانات اضافی با فرکانس‌های $\omega _{\alpha }\pm \omega _{\beta }$ می‌شود.

ناهماهنگی همچنین نمایه انرژی منحنی تشدید را اصلاح می‌کند که منجر به پدیده‌های جالبی مانند اثر فولدوور و رزونانس ابرهماهنگ می‌شود.

اصل کلی[ویرایش]

نوسانات هماهنگ درمقابل ناهماهنگ

"جرم و فنر" یک نمونه کلاسیک از نوسانات هماهنگ است. بسته به مکان جرم،

x

، نیروی بازگشتی را به سمت وسط تجربه خواهد کرد. نیروی بازگشتی متناسب با

x

است، بنابراین سامانه حرکت هماهنگ ساده ای را نشان می‌دهد.

آونگ یک نوسان‌ساز ساده "هماهنگ" است. بسته به موقعیت زاویه ای جرم

θ

، یک نیروی بازگرداننده مختصات

θ

را به سمت وسط به عقب می‌راند. این نوسان‌ساز ناهماهنگ است زیرا نیروی بازگرداننده با

θ

متناسب نیست، بلکه متناسب با

sin(θ)

است. چون تابع خطی

y = θ

تقریبی از تابع غیرخطی

y = sin(θ)

است وقتی

θ

کوچک است، سامانه می‌تواند به صورت یک نوسان‌گر هماهنگ برای نوسان‌های کوچک مدل‌سازی شود.

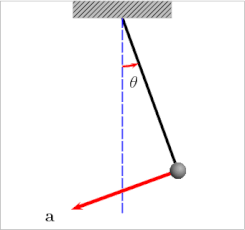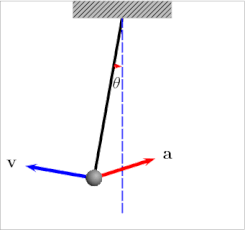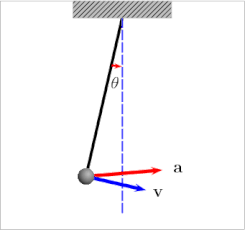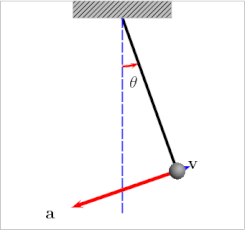
نوسانگر یک سامانه فیزیکی است که با حرکت تناوبی مانند آونگ، تیون چنگالی یا مولکول دواتمی ارتعاشی مشخص می‌شود. از نظر ریاضی، ویژگی اساسی یک نوسانگر این است که برای برخی از مختصات $x$ از سامانه، نیرویی که بزرگی آن به $x$ بستگی دارد، $x$ از مقادیر نهایی دور کرده و به سمت مقدار مرکزی $x 0$ برمی‌گرداند و باعث می‌شود $x$ بین کرانه‌ها نوسان کند. به عنوان مثال، $x$ ممکن است نشان دهنده جابجایی آونگ از موقعیت استراحت آن $x =۰$ باشد. همان‌طور که قدرمطلق $x$ افزایش می‌یابد، نیروی بازگردانی که بر وزن آونگ وارد می‌شود و آن را به سمت وضعیت استراحت خود به عقب می‌راند، افزایش می‌یابد.

در نوسانگرهای هماهنگ، نیروی بازگشت از نظر بزرگی (و در جهت مخالف) با جابجایی $x$ از موقعیت طبیعی آن $x 0$ متناسب است. معادله دیفرانسیل حاصل حاکی از آن است که $x$ باید در طول زمان به‌صورت سینوسی نوسان داشته باشد، با دوره‌تناوبی از نوسان که ذاتی سامانه است. $x$ ممکن است با هر دامنه ای نوسان داشته باشد، اما همیشه یک دوره‌تناوب خواهد داشت.

با این حال، نوسانگرهای ناهماهنگی با وابستگی غیرخطی نیروی بازگشتی به جابجایی x مشخص می‌شوند. درنتیجه، دوره‌تناوب نوسان‌ساز ناهماهنگ ممکن است به دامنه نوسان آن بستگی داشته باشد.

درنتیجه غیرخطی بودن نوسانگرهای ناهماهنگ، فرکانس ارتعاش می‌تواند بسته به جابجایی سامانه تغییر کند. این تغییرات در فرکانس ارتعاش منجر به تزویج (به انگلیسی: coupled) شدن انرژی از فرکانس اصلی ارتعاش به فرکانس‌های دیگر از طریق فرآیندی به نام تزویج‌سازی پارامتری (به انگلیسی: parametric coupling) می‌شود.^{^{[نیازمند شفاف‌سازی]}}

در نظر گرفتن نیروی بازگشتی غیرخطی به عنوان تابع $F (x - x 0)$ از جابجایی x از موقعیت طبیعی آن، ممکن است $F$ با تقریب خطی آن $F 1 = F' (0) \cdot (x - x 0)$ در جابجایی صفر جایگزین کنیم. تابع تقریبی F₁ خطی است، بنابراین حرکت هماهنگی ساده را توصیف می‌کند. علاوه بر این، این تابع $F 1$ زمانی دقیق است که $x - x 0$ کوچک باشد. به همین دلیل می‌توان حرکت ناهماهنگی را تا زمانی که نوسانات کوچک باشد به عنوان حرکت هماهنگ تقریب زد.

نمونه‌هایی در فیزیک[ویرایش]

سامانه‌های زیادی در سراسر جهان فیزیکی وجود دارند که می‌توان آن‌ها را علاوه بر سامانه‌های غیرخطی جرم - فنر، به‌عنوان نوسانگرهای ناهماهنگ مدل‌سازی کرد. به عنوان مثال، یک اتم که از یک هسته با بار مثبت تشکیل شده است که توسط یک ابر الکترونیکی با بار منفی احاطه شده است، زمانی که یک میدان الکتریکی وجود دارد، جابجایی بین مرکز جرم هسته و ابر الکترونیکی را تجربه می‌کند. مقدار آن جابجایی که ممان دوقطبی الکتریکی نامیده می‌شود، به صورت خطی با میدان اعمال شده برای میدان‌های کوچک مرتبط است، اما با افزایش بزرگی میدان، رابطه گشتاور دوقطبی میدان غیرخطی می‌شود، درست مانند سامانه مکانیکی.

نمونه‌های بیشتری از نوسان‌سازهای ناهماهنگ شامل آونگ با زاویه بزرگ است. نیم‌رساناهای غیرتعادلی که دارای انبوهه حامل گرم زیادی هستند که رفتارهای غیرخطی از انواع مختلف مربوط به جرم مؤثر حامل‌ها را نشان می‌دهند. و پلاسمای یونوسفر، که همچنین رفتار غیرخطی بر اساس ناهماهنگی پلاسما، رشته‌های نوسان عرضی از خود نشان می‌دهند. در واقع، تقریباً همه نوسانگرها زمانی ناهماهنگ می‌شوند که دامنه پمپ آنها فراتر از آستانه افزایش یابد و درنتیجه لازم است از معادلات غیرخطی حرکت برای توصیف رفتار آنها استفاده شود.

ناهماهنگی در شبکه و ارتعاشات مولکولی، در نوسانات کوانتومی^[۱] و در آکوستیک نقش دارد. اتم‌های موجود در یک مولکول یا یک جامد در مورد موقعیت‌های تعادلی خود ارتعاش می‌کنند. هنگامی که این ارتعاشات دارای دامنه‌های کوچک هستند، می‌توانند توسط نوسانگرهای هماهنگ توصیف شوند. با این حال، هنگامی که دامنه‌های ارتعاش بزرگ هستند، به عنوان مثال در دماهای بالا، ناهماهنگی مهم می‌شود. نمونه ای از اثرات ناهماهنگی، انبساط حرارتی جامدات است که معمولاً با تقریب شبه‌هماهنگ مورد مطالعه قرار می‌گیرد. مطالعه سامانه‌های ناهماهنگ ارتعاشی با استفاده از مکانیک کوانتومی یک کار محاسباتی سخت است زیرا ناهماهنگی نه تنها پتانسیل تجربه شده توسط هر نوسان‌گر را پیچیده‌تر می‌کند، بلکه تزویج بین نوسان‌گرها را نیز درنظر می‌گیرد. می‌توان از روش‌های اصول اولی مانند نظریه تابعی-چگالی برای ترسیم پتانسیل ناهماهنگ تجربه شده توسط اتم‌ها در هر دو مولکول^[۲] و جامدات استفاده کرد.^[۳] انرژی‌های ارتعاشی ناهماهنگ دقیق را می‌توان با حل معادلات ارتعاشی ناهماهنگ برای اتم‌ها در یک نظریه میدان میانه به‌دست‌آورد. درنهایت، می‌توان از نظریه آشفتگی مولر-پلست برای فراتر رفتن از فرم‌بندی میدان میانه استفاده کرد.

دوره‌تناوب نوسانات[ویرایش]

یک جرم $m$ را در نظر بگیرید حرکت در یک چاه پتانسیل $U(x)$ . دوره‌تناوب نوسان ممکن است مشتق شود^[۴] $T={\sqrt {2m}}\int _{x_{-}}^{x_{+}}{\frac {dx}{\sqrt {E-U(x)}}}$ که در آن کرانه حرکت توسط $x_{-}<x<x_{+}$ و $U(x_{-})=U(x_{+})=E$ داده می‌شود.

جستارهای وابسته[ویرایش]

منابع[ویرایش]

Landau, L. D.; Lifshitz, E. M. (1976), Mechanics (3rd ed.), Pergamon Press, ISBN 978-0-08-021022-3
Filipponi, A.; Cavicchia, D. R. (2011), "Anharmonic dynamics of a mass O-spring oscillator", American Journal of Physics, 79 (7): 730–735, Bibcode:2011AmJPh..79..730F, doi:10.1119/1.3579129

↑ Lim, Kieran F.; Coleman, William F. (August 2005), "The Effect of Anharmonicity on Diatomic Vibration: A Spreadsheet Simulation", J. Chem. Educ., 82 (8): 1263, Bibcode:2005JChEd..82.1263F, doi:10.1021/ed082p1263.1
↑ Jung, J. O.; Benny Gerber, R. (1996), "Vibrational wave functions and spectroscopy of (H₂O)_n, n=2,3,4,5: Vibrational self-consistent field with correlation corrections", J. Chem. Phys., 105 (23): 10332, Bibcode:1996JChPh.10510332J, doi:10.1063/1.472960
↑ Monserrat, B.; Drummond, N.D.; Needs, R.J. (2013), "Anharmonic vibrational properties in periodic systems: energy, electron-phonon coupling, and stress", Phys. Rev. B, 87 (14): 144302, arXiv:1303.0745, Bibcode:2013PhRvB..87n4302M, doi:10.1103/PhysRevB.87.144302
↑ Amore, Paolo; Fernández, Francisco M. (2005). "Exact and approximate expressions for the period of anharmonic oscillators". European Journal of Physics. 26 (4): 589–601. arXiv:math-ph/0409034. Bibcode:2005EJPh...26..589A. doi:10.1088/0143-0807/26/4/004.

پیوند به بیرون[ویرایش]

Elmer, Franz-Josef (July 20, 1998), Nonlinear Resonance, University of Basel, archived from the original on June 13, 2011, retrieved October 28, 2010

[1] Lim, Kieran F.; Coleman, William F. (August 2005), "The Effect of Anharmonicity on Diatomic Vibration: A Spreadsheet Simulation", J. Chem. Educ., 82 (8): 1263, Bibcode:2005JChEd..82.1263F, doi:10.1021/ed082p1263.1

[2] Jung, J. O.; Benny Gerber, R. (1996), "Vibrational wave functions and spectroscopy of (H₂O)_n, n=2,3,4,5: Vibrational self-consistent field with correlation corrections", J. Chem. Phys., 105 (23): 10332, Bibcode:1996JChPh.10510332J, doi:10.1063/1.472960

[3] Monserrat, B.; Drummond, N.D.; Needs, R.J. (2013), "Anharmonic vibrational properties in periodic systems: energy, electron-phonon coupling, and stress", Phys. Rev. B, 87 (14): 144302, arXiv:1303.0745, Bibcode:2013PhRvB..87n4302M, doi:10.1103/PhysRevB.87.144302

[4] Amore, Paolo; Fernández, Francisco M. (2005). "Exact and approximate expressions for the period of anharmonic oscillators". European Journal of Physics. 26 (4): 589–601. arXiv:math-ph/0409034. Bibcode:2005EJPh...26..589A. doi:10.1088/0143-0807/26/4/004.

[۱]

[۲]

[۳]

[۴]