پدیده انتشار
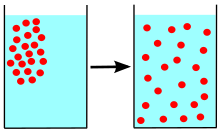
نفوذ یا انتشار (به انگلیسی: Diffusion) به طور کلی، مجموع حرکت هرچیزی (به طور مثال: اتمها، یونها، مولکولها و انرژی) از محلی با غلظت بالاتر به محلی با غلظت کمتر میباشد. نفوذ ناشی از گرادیانی در انرژی آزاد گیبس یا پتانسیل شیمیایی میباشد.
ممکن است که نفوذ را به طور عکس و در خلاف جهت گرادیان غلظت انجام دهیم مانند تجزیه اسپینودال. نکته قابل توجه این است که نفوذ، یک پدیدهای است که به علت حرکت تصادفی مولکولها، ماهیتی تصادفی دارد. از این رو میتوان برای مدلسازی بسیاری از پدیدههای زندگی روزمره از آن استفاده کرد مانند: علم آمار، نظریه احتمالات، فیزیک، زیستشناسی، اقتصاد، مارکتینگ و امور مالی (نفوذ در ایدهها ، اطلاعات، قیمتها).
تمام زمینههای ذکر شده در بالا، مدلهای ریاضی مشابهی را استفاده میکنند و ایدهی کلی احاطه کننده این پدیده که در موارد بالا کاربرد دارد این است که: ماده یا مورد قابل بررسی ما که دچار پدیده انتشار شده است از مکان یا موقعیتی که غلظت بالاتر دارد به سمت مکانی با غلظت کمتر حرکت خواهد کرد.

یکی از ویژگیهای خاص نفوذ این است که به حرکت تصادفی ذرات وابسته است و منجر به مخلوط شدن یا انتقال جرم بدون نیاز به حرکت تودهای میشود. حرکت توده ای از ویژگی های فرارفت است. اصطلاح همرفت برای توصیف ترکیبی از هر دو پدیده انتقال ذکر شده میباشد.
اگر بتوان یک پدیده انتشار را با قوانین فیک توصیف کرد، به آن انتشار عادی میگویند. در غیر این صورت، به آن انتشار غیرعادی میگویند.
وقتی بحث میزان انتشار در میان است، از دو مقیاس طول در دو سناریو مختلف استفاده میشود:
- حرکت براونی یک منبع تکانشی (مثلاً یک اسپری عطر): . n بعد این حرکت براونی است.
2. منبع غلظت ثابت در یک بعد - طول انتشار: در انتشار فیکی، این موضوع را با فرمول بیان میکنیم.
انتشار و جریان تودهای
[ویرایش](جریان تودهای) حرکت/جریان کل بدنه به دلیل گرادیان فشار (مثلاً خروج آب از شیر آب) است. "انتشار" حرکت تدریجی به دلیل گرادیان غلظت، بدون حرکت خالص ماده است. نمونه ای از فرآیندی که در آن هر دو حرکت تودهای و انتشار رخ میدهد، تنفس انسان است.
تشریح نقش انتشار و جریان تودهای
[ویرایش]اول، یک فرآیند "جریان تودهای" وجود دارد. ریهها در حفره قفسه سینه قرار دارند که به عنوان اولین مرحله در تنفس خارجی منبسط میشود. این انبساط منجر به افزایش حجم آلوئولها در ریهها میشود که باعث کاهش فشار در آلوئولها میشود. این یک گرادیان فشار بین هوای خارج از بدن با فشار نسبتاً بالا و آلوئولها در فشار نسبتاً کم ایجاد میکند. هوا در شیب فشار از طریق راههای هوایی ریهها و داخل آلوئولها حرکت میکند تا زمانی که فشار هوا و فشار هوا در آلوئولها برابر شوند، یعنی زمانی که دیگر گرادیان فشار وجود نداشته باشد، حرکت هوا توسط جریان تودهای متوقف میشود. .
دوم، یک فرآیند "انتشار" وجود دارد. هوای وارد شده به آلوئولها دارای غلظت بیشتری از اکسیژن نسبت به هوای "کهنه" موجود در آلوئولها است. افزایش غلظت اکسیژن باعث ایجاد گرادیان غلظتی برای اکسیژن بین هوای موجود در آلوئولها و خون در مویرگ هایی میشود که آلوئولها را احاطه کردهاند. سپس اکسیژن با انتشار، به سمت پایین گرادیان غلظت، به داخل خون حرکت میکند. پیامد دیگر ورود هوا به آلوئولها این است که غلظت دی اکسید کربن در آلوئولها کاهش مییابد. این باعث ایجاد گرادیان غلظتی برای انتشار دی اکسید کربن از خون به داخل آلوئولها میشود، زیرا هوای تازه دارای غلظت بسیار کم دی اکسید کربن در مقایسه با خون در بدن است.
سوم، یک فرآیند "جریان تودهای" دیگر وجود دارد. عمل پمپاژ قلب سپس خون را به سراسر بدن منتقل میکند. با انقباض بطن چپ قلب، حجم آن کاهش مییابد که باعث افزایش فشار در بطن میشود. این یک گرادیان فشار بین قلب و مویرگها ایجاد میکند و خون از طریق رگهای خونی با جریان تودهای به سمت پایین گرادیان فشار حرکت میکند.
انتشار در زمینه رشتههای مختلف
[ویرایش]مفهوم انتشار به طور گستردهای در: فیزیک (انتشار ذرات)، شیمی، زیست شناسی، جامعه شناسی، اقتصاد و امور مالی (انتشار افراد، ایدهها و ارزشهای قیمت) استفاده میشود. با این حال، در هر مورد، ماده یا مجموعهای که تحت انتشار قرار میگیرد، از نقطه یا مکانی که غلظت بیشتری از آن ماده یا مجموعه وجود دارد، "گسترش مییابد".
دو راه برای معرفی مفهوم انتشار وجود دارد:
1. یک رویکرد پدیدارشناختی که با قوانین انتشار فیک و پیامدهای ریاضی آنها شروع میشود.
2. یک رویکرد فیزیکی و اتمی، با در نظر گرفتن راه رفتن تصادفی ذرات در حال انتشار.[3]
در رویکرد پدیدارشناسی، انتشار حرکت یک ماده از ناحیهای با غلظت بالا به ناحیهای با غلظت کم بدون حرکت تودهای است. طبق قوانین فیک، شار انتشار متناسب با منفی گرادیان غلظتها است. از مناطق با غلظت بالاتر به مناطق با غلظت پایینتر میرود. مدتی بعد، تعمیمهای مختلفی از قوانین فیک در چارچوب ترمودینامیک و ترمودینامیک غیرتعادلی ایجاد شد.[4]

از دیدگاه اتمی، انتشار به عنوان یک نتیجه از راه رفتن تصادفی ذرات منتشر در نظر گرفته میشود. در انتشار مولکولی، مولکولهای متحرک توسط انرژی حرارتی خود رانده میشوند. راه رفتن تصادفی ذرات کوچک در حالت تعلیق در یک سیال در سال 1827 توسط رابرت براون کشف شد، او متوجه شد که ذره ریز معلق در یک محیط مایع و به اندازه کافی بزرگ است که در زیر میکروسکوپ نوری قابل مشاهده باشد، حرکت سریع و دائماً نامنظم ذرات را نشان میدهد. جنبش براونی تئوری حرکت براونی و زمینه های اتمی انتشار توسط آلبرت انیشتین ایجاد شد.[5] مفهوم انتشار معمولاً در مورد هر موضوعی که شامل پیاده روی تصادفی در گروههای افراد است به کار میرود.
در زمینه رشته مهندسی مواد
[ویرایش]در شیمی و علم و مهندسی مواد، انتشار به حرکت مولکول های سیال در جامدات متخلخل اشاره دارد.[6] انتشار مولکولی زمانی اتفاق میافتد که احتمال برخورد با مولکول دیگر بیشتر از برخورد با دیوارههای منافذ باشد. در چنین شرایطی، انتشار مشابه با فضای غیرمحدود است و با میانگین مسیر آزاد متناسب است. انتشار نادسن زمانی اتفاق میافتد که قطر منافذ قابل مقایسه یا کوچکتر از میانگین مسیر آزاد مولکولی باشد که در منافذ منتشر میشود. در این شرایط به تدریج احتمال برخورد با دیواره های منافذ بیشتر میشود و نفوذ پذیری کمتر میشود. در نهایت انتشار پیکربندی وجود دارد، که اگر اندازه مولکولها با منافذ قابل مقایسه باشد، اتفاق میافتد. در این شرایط، انتشار در مقایسه با انتشار مولکولی بسیار کمتر است و تفاوت های کوچک در قطر جنبشی مولکول باعث تفاوت های زیادی در انتشار میشود.
در زمینه رشته زیستشناسی
[ویرایش]زیست شناسان اغلب از اصطلاحات "حرکت خالص" یا "انتشار خالص" برای توصیف حرکت یون ها یا مولکول ها توسط انتشار استفاده میکنند. به عنوان مثال، تا زمانی که غلظت اکسیژن در خارج از سلول وجود داشته باشد، اکسیژن میتواند از طریق غشای سلولی پخش شود. با این حال، از آنجایی که حرکت مولکولها تصادفی است، گاهی اوقات مولکول های اکسیژن از سلول خارج میشوند (بر خلاف گرادیان غلظت). از آنجایی که تعداد مولکول های اکسیژن در خارج از سلول بیشتر است، احتمال اینکه مولکول های اکسیژن وارد سلول شوند بیشتر از احتمال خروج مولکول های اکسیژن از سلول است. بنابراین، حرکت خالص مولکول های اکسیژن (تفاوت بین تعداد مولکول های ورودی یا خروجی از سلول) به داخل سلول است. به عبارت دیگر، یک حرکت خالص مولکول های اکسیژن به سمت پایین گرادیان غلظت وجود دارد.
تاریخچه انتشار (نفوذ)
[ویرایش]در گذر زمان، انتشار در جامدات مدت ها قبل از ایجاد نظریه انتشار مورد استفاده قرار گرفته بود. به عنوان مثال، پلینیوس قبلاً فرآیند سیمانکاری را توضیح داده بود که از طریق انتشار کربن، فولاد را از عنصر آهن (Fe) تولید میکند. نمونه دیگر برای قرن ها به خوبی شناخته شده است، انتشار رنگ شیشههای رنگی یا سفالی و سرامیکهای چینی.
در علم مدرن، اولین مطالعه تجربی سیستماتیک انتشار توسط توماس گراهام انجام شد. او انتشار در گازها را مطالعه کرد و پدیده اصلی توسط او در سال های 1831-1831 شرح داده شد:[7]
«...گازهای با ماهیت متفاوت، هنگامیکه با هم تماس پیدا میکنند، خود را بر اساس چگالی خود، سنگین ترین زیرترین و سبک ترترین قسمت بالایی قرار نمیدهند، بلکه به طور خود به خود، متقابلاً و به طور مساوی، از طریق یکدیگر پخش میشوند و بنابراین در آن حالت، مخلوط گازی برای هر مدت زمانی باقی خواهد ماند."
اندازهگیریهای گراهام به جیمز کلرک ماکسول کمک کرد که در سال 1867 ضریب انتشار CO2 در هوا را بدست آورد که میزان خطای آن کمتر از 5 درصد است.
در سال 1855، آدولف فیک، 26 ساله، شرح دهنده آناتومی از زوریخ، قانون انتشار خود را پیشنهاد کرد. او از تحقیقات گراهام استفاده کرد و هدف خود را "توسعه یک قانون اساسی برای عملکرد انتشار در یک عنصر واحد از فضا" عنوان کرد. او تشابه عمیقی را بین انتشار و هدایت گرما یا الکتریسیته بیان کرد و فورمولاسیونی مشابه قانون فوریه برای هدایت گرما (1822) و قانون اهم برای جریان الکتریکی (1827) ایجاد کرد.
رابرت بویل در قرن هفدهم [8] با نفوذ روی در یک سکه مسی، انتشار در جامدات را نشان داد. با این وجود، انتشار در جامدات تا نیمه دوم قرن نوزدهم به طور سیستماتیک مورد مطالعه قرار نگرفت. ویلیام چندلر رابرتز آستن، متالورژیست معروف بریتانیایی و دستیار سابق توماس گراهام، به طور سیستماتیک انتشار حالت جامد را بر روی نمونه طلا در سرب در سال 1896 مطالعه کرد. :[9]
"...ارتباط طولانی من با تحقیقات گراهام، تلاش برای گسترش کار او در مورد انتشار مایع به فلزات را تقریباً یک وظیفه کرد."
در سال 1858، رودولف کلازیوس مفهوم مسیر آزاد متوسط را معرفی کرد. در همان سال، جیمز کلرک ماکسول اولین نظریه اتمی را در مورد فرآیندهای انتقال گازها ارائه کرد. نظریه اتمی مدرن انتشار و حرکت براونی توسط آلبرت انیشتین، ماریان اسمولوچوفسکی و ژان باپتیست پرین ارائه شد. لودویگ بولتزمن، در توسعه پسزمینههای اتمی فرآیندهای انتقال ماکروسکوپی، معادله بولتزمن را معرفی کرد که بیش از 140 سال است که در خدمت ریاضیات و فیزیک بوده و منبع ایدهها و نگرانیهای پدیدههای انتقال بوده است.[10]
در سالهای 1920-1921، جورج دی هیوسی، خود انتشاری را با استفاده از ایزوتوپهای رادیویی اندازهگیری کرد. او به مطالعه خود انتشاری ایزوتوپ های رادیواکتیو سرب، در سرب مایع و جامد پرداخت.
Yakov Frenkel (گاهی اوقات، Jakov/Jacob Frenkel) ایده انتشار در کریستال ها از طریق نابهجاییها (جای خالیها و اتم های بیننشین) را پیشنهاد و در سال 1926 توضیح داد. وی در پایان گفت: فرآیند انتشار در ماده متراکم مجموعهای از جهشهای اولیه و برهمکنشهای شبه شیمیایی ذرات و عیوب است. او چندین مکانیسم انتشار را معرفی کرد و ثابتهای سرعت را از دادههای تجربی پیدا کرد.
مدتی بعد، کارل واگنر و والتر اچ. شاتکی ایده های فرنکل را در مورد مکانیسم های انتشار، بیشتر توسعه دادند. در حال حاضر، به طور جهانی به رسمیت شناخته شده است که نابهجاییها و عیوب کریستالی برای انتشار در کریستالها ضروریاند.[9]
هنری آیرینگ، به همراه نویسندگان همکار، نظریه سرعت واکنش مطلق خود را در مدل شبه شیمیایی انتشار فرنکل به کار برد.[11] قیاس بین سینتیک واکنش و انتشار منجر به نسخههای غیرخطی مختلفی از قانون فیک میشود.[12]

مدل های پایهای انتشار (نفوذ)
[ویرایش]شار انتشار (نفوذ)
[ویرایش]هر مدل از انتشار، شار انتشار را با استفاده از غلظت ها، چگالی ها و مشتقات آنها بیان میکند. شار یک بردار است که در آن نشان دهنده مقدار و جهت انتقال است. با توجه به یک منطقه کوچک با نرمال ,
انتقال یک کمیت فیزیکی N از طریق منطقه در هر زمان است. با توجه به این موارد داریم:
در فرمول بالا داریم:
محصول داخلی است و نماد small-o است. اگر از نماد ناحیه برداری استفاده کنیم . سپس داریم:
بعد شار انتشار [شار] = [مقدار]/([زمان]·[مساحت]) است. کمیت فیزیکی در حال انتشار، N ممکن است تعداد ذرات، جرم، انرژی، بار الکتریکی یا هر کمیت عددی دیگری باشد. برای چگالی آن، n، معادله انتشار شکل زیر را دارد:
در این فرمول داریم:
W شدت هر منبع این کمیت است (مثلاً سرعت یک واکنش شیمیایی). برای معادله انتشار، شرایط مرزی بدون شار را میتوان به صورت فرمولاسیون بیان کرد: در مرز، جایی که نسبت نرمال به مرز در نقطه X است.
قانون فیک و معادلات مربوطه
[ویرایش]معادلات مربوط به این بخش را میتوان در مقاله قوانین نفوذ فیک به طور کامل مطالعه و مشاهده کرد اما به طور کلی موارد آن به شرح زیر است:
قانون اول فیک: شار انتشار متناسب با منفی گرادیان غلظت هست
معادله انتشار متناظر (قانون دوم فیک) به شرح زیر است:
که در آن, عملگر لاپلاس است:
معادلات اونزاگر برای انتشار چند جزئی و انتشار گرما
[ویرایش]قانون فیک انتشار یک ماده افزودنی را در یک محیط توصیف میکند. غلظت این مخلوط باید کم و گرادیان این غلظت نیز کم باشد. نیروی محرکه انتشار در قانون فیک ضد گرادیان غلظت است. در سال 1931، لارس اونزاگر[13] پدیدههای انتقال چند جزئی را در زمینه کلی ترمودینامیک خطی غیرتعادلی گنجاند. برای پدیدههای انتقال چند جزئی داریم:
که در آن J، شار i امین کمیت فیزیکی (مولفه) است و j، X امین نیروی ترمودینامیکی است.
نیروهای ترمودینامیکی برای فرآیندهای انتقال توسط اونزاگر به عنوان شیب فضایی مشتقات چگالی آنتروپی s معرفی شدند (او از اصطلاح "نیرو" در علامت نقل قول یا "نیروی محرک" استفاده کرد):
در آن n، مختصات ترمودینامیکی هستند. برای انتقال گرما و جرم میتوانیم، n0=u (چگالی انرژی داخلی) و n_{i} غلظت جزء i ام نیروهای محرک مربوطه بردارهای فضا هستند کمک بگیریم:
به علت اینکه
که در آن T دمای مطلق و پتانسیل شیمیایی جزء i ام است. باید تاکید کرد که معادلات انتشار جداگانه، اختلاط یا انتقال جرم را بدون جریان تودهای توصیف میکنند. بنابراین، شرایط مربوط به تغییر فشار کل نادیده گرفته میشود. برای انتشار مواد افزودنی کوچک و برای شیب های کوچک امکان پذیر است.
برای معادلات اونزاگر خطی، باید نیروهای ترمودینامیکی را در تقریب خطی نزدیک به تعادل بگیریم:
که در آن مشتقات s در تعادل محاسبه میشوند. ماتریس ضرایب جنبشی باید متقارن (روابط متقابل اونزاگر) و قطعی مثبت (برای رشد آنتروپی) باشد.
معادلات انتقال به شرح زیر هستند:
در اینجا تمام شاخص های i، j، k = 0، 1، 2، ... مربوط به انرژی داخلی (0) و اجزای مختلف است. عبارت در پرانتز مربع ماتریس انتشار (i,k > 0)،ضرایب نفوذ گرما (i > 0، k = 0 یا k > 0، i = 0) و هدایت حرارتی (i = k = 0) است.
در شرایط همدما T = ثابت. پتانسیل ترمودینامیکی مربوطه انرژی آزاد (یا آنتروپی آزاد) است. نیروهای محرک ترمودینامیکی برای انتشار همدما، ضد گرادیان پتانسیلهای شیمیایی، هستند و ماتریس ضرایب انتشار است.
(i,k > 0)
در تعریف نیروهای ترمودینامیکی و ضرایب جنبشی دلبخواهی ذاتی وجود دارد زیرا آنها به طور جداگانه قابل اندازهگیری نیستند و فقط ترکیب آنها قابل اندازهگیری است. به عنوان مثال، در کار اصلی اونزاگر [13] نیروهای ترمودینامیکی شامل ضرب اضافی T است، در حالی که در دوره فیزیک نظری [14] این ضریب حذف شده اما علامت نیروهای ترمودینامیکی مخالف است. همه این تغییرات با تغییرات مربوطه در ضرایب تکمیل میشود و بر مقادیر قابل اندازه گیری تأثیر نمی گذارد.
انتشار غیر قطری باید غیرخطی باشد
[ویرایش]فرمولاسیون ترمودینامیک برگشت ناپذیر خطی (اونزاگر) سیستم های معادلات انتشار خطی را در قالب معادله زیر ایجاد میکند:
اگر ماتریس ضرایب انتشار مورب باشد، این سیستم معادلات فقط مجموعه ای از معادلات فیک جدا شده برای اجزای مختلف است. فرض کنید که انتشار غیر قطری است، برای مثال، ، و حالت را با در نظر بگیرید. در این حالت، . اگر در برخی نقاط ، آنگاه در مدت کوتاهی در این نقاط منفی میشود. بنابراین، انتشار غیر قطری خطی، مثبت بودن غلظت ها را حفظ نمیکند. معادلات غیر قطری انتشار چند جزئی باید غیرخطی باشند.[12]
تحرک انیشتین و فرمول تئورل
[ویرایش]رابطه انیشتین (نظریه جنبشی) ضریب انتشار و تحرک (نسبت سرعت رانش نهایی ذره به نیروی اعمال شده) را به هم متصل میکند.[15] برای ذرات باردار داریم:
که در آن D ثابت انتشار، μ «تحرک»، kB ثابت بولتزمن، T دمای مطلق، و q بار اولیه، یعنی بار یک الکترون است.
در زیر، برای ترکیب پتانسیل شیمیایی μ و تحرک در همان فرمول، از علامت برای تحرک استفاده میکنیم. رویکرد مبتنی بر تحرک بیشتر توسط ر اعمال شد.[16] در سال 1935، او انتشار یون ها از طریق یک غشاء را مطالعه کرد. او ماهیت رویکرد خود را در فرمول بیان کرد:
شار برابر است با تحرک × غلظت × نیرو در هر گرم یون.
این به اصطلاح فرمول تئورل است. اصطلاح "گرم یون" ("گرم ذره") برای مقداری از ماده ای استفاده میشود که حاوی تعداد یون ها (ذرات) آووگادرو باشد. اصطلاح رایج امروزی مول است.
نیرو در شرایط همدما از دو بخش تشکیل شده است:
- نیروی انتشار ناشی از گرادیان غلظت:
- نیروی الکترواستاتیک ناشی از گرادیان پتانسیل الکتریکی:
در اینجا R ثابت گاز است، T دمای مطلق، n غلظت است، غلظت تعادل با یک بالانویس "eq" مشخص میشود، q بار و φ پتانسیل الکتریکی است.
تفاوت ساده اما مهم بین فرمول تئورل و قوانین اونزاگر، ضریب غلظت در عبارت تئورل برای شار است. در رویکرد انیشتین-تئورل، اگر برای نیروی محدود، غلظت به سمت صفر میل میکند، شار نیز به صفر میل میکند، در حالی که معادلات اونزاگر این قانون ساده و از نظر فیزیکی واضح را نقض میکند
فرمول کلی فرمول تئورل برای سیستم های غیر کامل تحت شرایط همدما به این صورت است [12]:
جایی که μ پتانسیل شیمیایی است، μ0 مقدار استاندارد پتانسیل شیمیایی است. عبارت به اصطلاح فعالیت است. "غلظت موثر" یک گونه را در یک مخلوط غیر ایده آل اندازه گیری میکند. در این نماد، فرمول تئورل برای شار شکل بسیار ساده ای دارد[12]:
مشتق استاندارد فعالیت شامل یک ضریب عادی سازی و برای غلظت های کوچک ، که در آن غلظت استاندارد است. بنابراین، این فرمول برای شار، شار کمیت بدون بعد نرمال شده را توصیف میکند:
قضیه نوسان اتلاف
[ویرایش]قضیه نوسان اتلاف بر اساس معادله لانژوین برای گسترش مدل انیشتین به مقیاس زمانی بالستیک توسعه یافته است.[17] به گفته لانگوین، این معادله بر اساس قانون دوم حرکت نیوتن است
که در آن داریم:
x موقعیت است.
μ تحرک ذره در سیال یا گاز است که با استفاده از رابطه انیشتین (نظریه جنبشی) قابل محاسبه است.
m جرم ذره است.
F نیروی تصادفی اعمال شده به ذره است.
t زمان است.
با حل این معادله، ثابت انتشار وابسته به زمان در محدوده طولانی مدت و زمانی که ذره به طور قابل توجهی چگال تر از سیال اطراف است، به دست می آید، [17]
که در آن داریم:
Kb ثابت بولتزمن است.
T دمای مطلق است.
μ تحرک ذره در سیال یا گاز است که با استفاده از رابطه انیشتین (نظریه جنبشی) قابل محاسبه است.
m جرم ذره است.
t زمان است.
فرمول تئورل برای انتشار چند جزئی
[ویرایش]فرمول تئورل با ترکیبی از تعریف اونزاگر از نیروی انتشار به دست میدهد
که در آن تحرک جزء i ام است، فعالیت آن است، ماتریس ضرایب است، نیروی انتشار ترمودینامیکی است، . برای سیستمهای کامل همدما، . بنابراین، رویکرد انیشتین-تئورل تعمیم چند جزئی زیر را از قانون فیک برای انتشار چند جزئی ارائه میدهد:
که در آن ماتریس ضرایب است. فرمول چاپمن-انسکوگ برای انتشار در گازها دقیقاً همان عبارات را شامل میشود. پیش از این، چنین اصطلاحاتی در معادله انتشار ماکسول-استفان معرفی شده بودند.
پرشها، روی سطح و داخل جامدات
[ویرایش]
انتشار معرف ها در سطح یک کاتالیزور ممکن است نقش مهمی در کاتالیز ناهمگن ایفا کند. مدل انتشار در تک لایه ایده آل بستگی به پرش معرف ها در نزدیکترین مکان های آزاد دارد. این مدل برای اکسیداسیون CO بر روی پلاتین تحت فشار کم گاز استفاده شد.
این سیستم شامل چندین معرف به شرح: روی سطح است. غلظت سطح آنها را میتوان با نشان داد.سطح شبکه ای از مکان های جذب است. هر مولکول معرف مکانی را روی سطح پر میکند. برخی از مکان ها آزاد هستند. غلظت مکان های آزاد برابر با . مجموع همه شامل مکان های آزاد ثابت است، چگالی مکان های جذب b.
مدل پرش برای شار انتشار (i = 1، ...، n) میدهد:
معادله انتشار مربوطه این است:[12]
با توجه به قانون بقای , و سیستم معادلات انتشار m را داریم. برای یک جزء، قانون فیک و معادلات خطی را دریافت میکنیم. برای دو یا چند جزء معادلات غیر خطی هستند. اگر همه ذرات بتوانند موقعیت خود را با نزدیکترین همسایگان خود مبادله کنند، یک تعمیم ساده به دست می آید:
که در آن یک ماتریس متقارن از ضرایب است که شدت پرش ها را مشخص میکند. مکان های آزاد (جای خالی) باید به عنوان "ذرات" خاص با غلظت در نظر گرفته شود.
نسخه های مختلف این مدل های پرش برای مکانیسم های انتشار ساده در جامدات نیز مناسب هستند.
انتشار در محیط متخلخل
[ویرایش]برای انتشار در محیط متخلخل، معادلات اصلی عبارتند از (اگر Φ ثابت باشد):[18]
که در آن D ضریب انتشار، Φ تخلخل، n غلظت، m> 0 است (معمولا m> 1، حالت m = 1 با قانون فیک مطابقت دارد).
باید دقت شود که تخلخل (Φ) محیط متخلخل هم در شرایط شار و هم در شرایط تجمع به درستی در نظر گرفته شود.[19] برای مثال، وقتی تخلخل به صفر میرسد، شار مولی در محیط متخلخل برای یک گرادیان غلظت معین به صفر میرسد. با اعمال واگرایی شار، شرایط تخلخل لغو میشود و معادله دوم بالا تشکیل میشود.
برای انتشار گازها در محیط متخلخل، این معادله رسمیت قانون دارسی است: شار حجمی گاز در محیط متخلخل برابر است با
که در آن k نفوذپذیری محیط، μ ویسکوزیته و p فشار است.
شار مولی اکتیو به صورت زیر داده شده است:
J = nq
و برای قانون دارسی معادله انتشار در محیط متخلخل را با m = γ + 1 به دست می آید. در محیط متخلخل، سرعت خطی متوسط (ν) به شار حجمی با رابطه زیر به یکدیگر مربوط میشوند:
ترکیب شار مولی فرارفتی با شار انتشاری معادله پراکندگی فرارفت را به دست میدهد.
برای نفوذ آب زیرزمینی، تقریب Boussinesq همان معادله را با m = 2 به دست میدهد.
برای پلاسمای با سطح تابش بالا، معادله زلدویچ-رایزر m> 4 را برای انتقال حرارت میدهد.
انتشار (نفوذ) در فیزیک
[ویرایش]ضریب انتشار در نظریه جنبشی گازها
[ویرایش]ضریب انتشار D ضریب قانون اول فیک است ، که در آن J شار انتشار (مقدار ماده) در واحد سطح در واحد زمان، n (برای مخلوط های ایده آل) غلظت و x موقعیت [طول] است.
دو گاز با مولکولهای هم قطر d و جرم m (خود انتشار) را در نظر بگیرید. در این مورد، نظریه مسیر آزاد متوسط ابتدایی انتشار برای ضریب انتشار به دست میآید.
که در آن kB ثابت بولتزمن، T دما، P فشار، ℓ میانگین مسیر آزاد و vT میانگین سرعت حرارتی است:
میبینیم که ضریب انتشار در تقریب مسیر آزاد متوسط با T به عنوان T3/2 رشد میکند و با P به عنوان 1/P کاهش مییابد. اگر برای P از قانون گاز ایده-آل P = RnT با غلظت کل n استفاده کنیم، میبینیم که برای غلظت معین n ضریب انتشار با T به عنوان T1/2 رشد میکند و برای دمای معین با غلظت کل به اندازه n/1 کاهش مییابد.

برای دو گاز مختلف، A و B، با جرمهای مولکولی mA، mB و قطر مولکولی dA, dB، میانگین تخمین مسیر آزاد ضریب انتشار A در B و B در A است:
در سینتیک بولتزمن از مخلوط گازها، هر گاز تابع توزیع خاص خود را دارد. ، جایی که t لحظه زمانی است، x موقعیت و c سرعت مولکول جزء یکم مخلوط است. هر جزء سرعت متوسط خود را دارد یعنی؛
اگر سرعت ها منطبق نیستند پس انتشار وجود دارد.
در تقریب چاپمن-انسکوگ، تمام توابع توزیع از طریق چگالی کمیت های حفظ شده بیان میشوند:[10]
- غلظت فردی ذرات، (ذرات در حجم)،
- چگالی حرکت (mi یکمین جرم ذره است)
- چگالی انرژی جنبشی:
دمای جنبشی T و فشار P در فضای سه بعدی به صورت زیر تعریف شده است:
جایی که چگالی کل است.
برای دو گاز، تفاوت بین سرعت، با عبارت زیر [10] داده میشود:
که در آن؛
نیرویی است که به مولکول های جزء i و نسبت انتشار حرارتی است.
ضریب مثبت است. این ضریب انتشار است. چهار عبارت در فرمول چهار اثر اصلی در انتشار گازها را توصیف میکند:
- شار مولفه اول را از نواحی با نسبت بالا به مناطق با مقادیر پایینتر توصیف میکند. از این نسبت (و به طور مشابه شار جزء دوم از زیاد به کم زیرا n2/n = 1 – n1/n)؛
- شار مولکولهای سنگینتر را به نواحی با فشار بالاتر و مولکولهای سبکتر را به مناطق با فشار پایینتر هدایت میکند، این بارودیفیوژن است.
- انتشار ناشی از تفاوت نیروهای اعمال شده به مولکول های انواع مختلف را توصیف میکند. به عنوان مثال، در میدان گرانشی زمین، مولکول های سنگین تر باید پایین بیایند، یا در میدان الکتریکی، مولکول های باردار حرکت کنند، تا زمانی که این اثر با مجموع عبارت های دیگر متعادل نشود این اثر را نباید با بارودیفیوژن ناشی از گرادیان فشار اشتباه گرفت.
- تشریح ترمودیفیوژن، شار انتشار ناشی از گرادیان دما است.
همه این اثرات انتشار نامیده میشوند زیرا تفاوت بین سرعت اجزای مختلف در مخلوط را توصیف میکنند. بنابراین، این اثرات را نمیتوان به عنوان یک جریان تودهای توصیف کرد و با فرارفت یا همرفت متفاوت است.
در اولین تقریب داریم، [10]
- برای کره های صلب؛
- برای دفع نیروی
عدد با ربعها تعریف میشود (فرمولهای (3.7)، (3.9)، فصل 10 از کتاب کلاسیک Chapman and Cowling[10])
میتوانیم ببینیم که وابستگی به T برای کرههای صلب مانند نظریه مسیر آزاد متوسط ساده است، اما برای قوانین دافعه توان، توان متفاوت است. وابستگی به غلظت کل n برای یک دمای معین همیشه یک ویژگی دارد، 1/n.
در کاربردهای دینامیک گاز، شار انتشار و جریان حجیم باید در یک سیستم معادلات انتقال به هم متصل شوند. جریان تودهای انتقال جرم را توصیف میکند. سرعت آن V سرعت متوسط جرمی است. از طریق چگالی تکانه و غلظت جرمی تعریف میشود:
جایی که غلظت جرمی گونه i است، چگالی جرم است.
طبق تعریف، سرعت انتشار جزء iام ، است. انتقال جرم مولفه i با معادله پیوستگی تعریف میشود:
در آن؛ نرخ خالص تولید انبوه در واکنش های شیمیایی است،
در این معادلات، اصطلاح فرارفت جزء i ام و اصطلاح نشان دهنده انتشار این جزء می باشد.
در سال 1948، Wendell H. Furry پیشنهاد کرد که از شکل نرخ انتشار یافت شده در نظریه جنبشی به عنوان چارچوبی برای رویکرد پدیدارشناختی جدید به انتشار در گازها استفاده شود. این رویکرد بیشتر توسط F.A. Williams و S.H. لام پیشرفت کرد.[20] آنها برای سرعت انتشار در گازهای چند جزئی (Nجزء) استفاده کردند:
اینجا، ماتریس ضریب انتشار، ضریب انتشار حرارتی، نیروی بدن در واحد جرم است که بر روی گونه i تأثیر می گذارد، کسر فشار جزئی از گونه i است (و فشار جزئی i است). کسر جرمی گونه i است و از طرفی داریم: .
انتشار الکترون ها در جامدات
[ویرایش]
هنگامی که چگالی الکترون ها در جامدات در تعادل نباشد، انتشار الکترون ها اتفاق میافتد. به عنوان مثال، هنگامی که یک بایاس به دو انتهای یک قطعه نیمه هادی اعمال میشود، یا نوری به یک طرف آن می تابد (شکل سمت چپ را ببینید)، الکترون ها از مناطق با چگالی بالا (مرکز) به مناطق با چگالی کم (دو انتها) پخش میشوند و یک گرادیان چگالی الکترون جریانی تولید میکند که به آن جریان انتشار میگویند.
جریان انتشار را میتوان با قانون اول فیک نیز توصیف کرد:
که در آن J چگالی جریان انتشار (مقدار ماده) در واحد سطح در واحد زمان است، n (برای مخلوط های ایده آل) چگالی الکترون است، x موقعیت [طول] است.
انتشار در ژئوفیزیک
[ویرایش]مدلهای تحلیلی و عددی که معادله انتشار را برای شرایط اولیه و مرزی مختلف حل میکنند، برای مطالعه طیف گستردهای از تغییرات در سطح زمین محبوب و مورد استفاده بودهاند. انتشار به طور گسترده در مطالعات فرسایش عقبنشینی شیب تپه، فرسایش بلوف، تخریب لکههای گسلی، عقبنشینی تراس/خط ساحلی برش موج، برش کانال آبرفتی، عقبنشینی فلات ساحلی و توسعه دلتا استفاده شده است.[21] اگرچه سطح زمین در بسیاری از این موارد به معنای واقعی کلمه پراکنده نیست، فرآیند انتشار به طور موثری از تغییرات کلی که در طول دهه ها تا هزاره ها رخ میدهد تقلید میکند. مدلهای انتشار، همچنین ممکن است برای حل مسائل ارزش مرزی معکوس استفاده شوند که در آنها برخی اطلاعات در مورد محیط رسوبی، از بازسازی دیرینه محیطی شناخته شده است و معادله انتشار برای تعیین هجوم رسوب و سری زمانی تغییرات شکل زمین استفاده میشود.[22]
دیالیز
[ویرایش]
دیالیز بر اساس اصول انتشار (نفوذ) املاح و اولترافیلتراسیون سیال در یک غشای نیمه تراوا کار میکند. انتشار از خواص مواد در آب است. مواد موجود در آب تمایل دارند از ناحیه ای با غلظت بالا به ناحیه ای با غلظت کم حرکت کنند.[23] خون در یک طرف یک غشای نیمه تراوا جریان دارد و یک ماده دیالیز یا مایع دیالیز ویژه در طرف مقابل جریان دارد. غشای نیمه تراوا یک لایه نازک از مواد است که حاوی سوراخ هایی با اندازه های مختلف یا منافذ است. املاح و مایعات کوچکتر از غشاء عبور میکنند، اما غشاء عبور مواد بزرگتر (مثلا گلبول های قرمز و پروتئین های بزرگ) را مسدود میکند. این فرآیند فیلترینگی را که در کلیه ها انجام میشود، تکرار میکند یعنی زمانی که خون وارد کلیه ها میشود و مواد بزرگتر از مواد کوچکتر در گلومرول جدا میشوند.[23]
راه رفتن تصادفی (حرکت تصادفی)
[ویرایش]یکی از تصورات غلط رایج این است که تک تک اتم ها، یون ها یا مولکول ها به طور تصادفی حرکت میکنند، که اینطور نیست. در انیمیشن سمت راست، به نظر می رسد یون در پانل سمت چپ در غیاب یون های دیگر دارای حرکت "تصادفی" است. همانطور که پانل سمت راست نشان میدهد، با این حال، این حرکت تصادفی نیست، بلکه نتیجه "برخورد" با یون های دیگر است. به این ترتیب، حرکت یک اتم، یون یا مولکول منفرد در یک مخلوط زمانی که به صورت مجزا مشاهده میشود، تصادفی به نظر میرسد. حرکت یک ماده در یک مخلوط با "راه رفتن تصادفی" توسط انرژی جنبشی درون سیستم کنترل میشود که میتواند تحت تأثیر تغییرات غلظت، فشار یا دما قرار گیرد. (این یک توصیف کلاسیک است. در مقیاس های کوچکتر، اثرات کوانتومی به طور کلی غیر قابل اغماض خواهند بود. بنابراین، مطالعه حرکت یک اتم منفرد ظریف تر میشود زیرا ذرات در چنین مقیاس های کوچکی با دامنه احتمال توصیف میشوند تا قطعی. اندازه گیری موقعیت و سرعت.)
جداسازی انتشار از همرفت در گازها
[ویرایش]در حالی که حرکت براونی ذرات مزوسکوپی چند مولکولی (مانند دانه های گرده مورد مطالعه براون) در زیر میکروسکوپ نوری قابل مشاهده است، انتشار مولکولی تنها در شرایط تجربی کنترل شده به دقت قابل بررسی است. از آنجایی که گراهام آزمایش میکند، به خوبی شناخته شده است که دوری کردن از همرفت ضروری است و این ممکن است یک کار غیر ضروری باشد.
در شرایط عادی، انتشار مولکولی تنها در طولهایی در محدوده نانومتر تا میلیمتر غالب است. در مقیاسهای طول بزرگتر، انتقال در مایعات و گازها معمولاً به دلیل پدیده انتقال دیگر، همرفت است. برای جداسازی انتشار در این موارد، تلاش های ویژه ای مورد نیاز است.
بنابراین، برخی از نمونههایی که اغلب ذکر میشوند اشتباه هستند: اگر ادکلن در یک مکان اسپری شود، به زودی در کل اتاق بوی آن به مشام میرسد، اما یک محاسبه ساده نشان میدهد که این نمیتواند به دلیل انتشار باشد. حرکت همرفتی در اتاق به دلیل دما [ناهمگنی] ادامه دارد. اگر جوهر در آب ریخته شود، معمولاً یک تکامل ناهمگن توزیع فضایی مشاهده میشود که به وضوح نشان دهنده همرفت (به ویژه در اثر این ریزش است).
در مقابل، انتقال گرما از طریق محیط جامد یک اتفاق روزمره است (به عنوان مثال، یک قاشق فلزی تا حدی در یک مایع داغ غوطه ور شده است). این توضیح میدهد که چرا انتشار گرما قبل از انتشار جرم به صورت ریاضی توضیح داده شده است.
انواع دیگر انتشار
[ویرایش]- انتشار ناهمسانگرد، همچنین به عنوان معادله Perona-Malik شناخته میشود، گرادیان های بالا را افزایش میدهد.
- انتشار اتمی، در جامدات
- انتشار بوم، انتشار پلاسما در میان میدان های مغناطیسی
- انتشار گردابی، در توصیف درشت دانه جریان آشفته
- انتشار گاز از سوراخ های کوچک
- انتشار الکترونیکی که در نتیجه جریان الکتریکی به نام جریان انتشار ایجاد میشود
- انتشار تسهیل شده، موجود در برخی از موجودات
- انتشار گازی که برای جداسازی ایزوتوپ استفاده میشود
- معادله گرما، انتشار انرژی حرارتی
- انتشار Itō، ریاضی سازی حرکت براونی، فرآیند تصادفی پیوسته.
- انتشار گاز نادسن در منافذ طولانی با برخوردهای مکرر دیواره
- پرواز Lévy
- انتشار مولکولی، انتشار مولکول ها از مناطق متراکم تر به مناطق کم تر
- انتشار مومنتوم سابق انتشار میدان سرعت هیدرودینامیکی
- انتشار فوتون
- انتشار پلاسما
- پیاده روی تصادفی، [24] مدلی برای انتشار
- انتشار معکوس، در برابر گرادیان غلظت، در جداسازی فاز
- انتشار چرخشی، جهت گیری مجدد تصادفی مولکول ها
- انتشار سطحی، انتشار ذرات روی سطح
- تاکسی، فعالیت حرکتی جهت دار حیوان در پاسخ به یک محرک است
- جنبش، فعالیت حرکتی غیر جهت دار حیوان در پاسخ به یک محرک است
- انتشار فرافرهنگی، انتشار صفات فرهنگی در سراسر منطقه جغرافیایی
- انتشار آشفته، انتقال جرم، گرما یا تکانه در یک سیال آشفته
جستارهای وابسته
[ویرایش]منابع
[ویرایش]- J.G. Kirkwood, R.L. Baldwin, P.J. Dunlop, L.J. Gosting, G. Kegeles (1960)Flow equations and frames of reference for isothermal diffusion in liquids. The Journal of Chemical Physics 33(5):1505–13.
- Muir, D. C. F. (1966-10-01). "Bulk flow and diffusion in the airways of the lung". British Journal of Diseases of the Chest. 60 (4): 169–176. doi:10.1016/S0007-0971(66)80044-X. ISSN 0007-0971. PMID 5969933.
- J. Philibert (2005). One and a half century of diffusion: Fick, Einstein, before and beyond. Archived 2013-12-13 at the Wayback Machine Diffusion Fundamentals, 2, 1.1–1.10.
- S.R. De Groot, P. Mazur (1962). Non-equilibrium Thermodynamics. North-Holland, Amsterdam.
- A. Einstein (1905). "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen" (PDF). Ann. Phys. 17 (8): 549–60. Bibcode:1905AnP...322..549E. doi:10.1002/andp.19053220806.
- Pescarmona, P.P. (2020). Gitis, V.; Rothenberg, G. (eds.). Handbook of Porous Materials. Vol. 4. Singapore: WORLD SCIENTIFIC. pp. 150–151. doi:10.1142/11909. ISBN 978-981-12-2328-0.
- Diffusion Processes, Thomas Graham Symposium, ed. J.N. Sherwood, A.V. Chadwick, W.M.Muir, F.L. Swinton, Gordon and Breach, London, 1971
- L.W. Barr (1997), In: Diffusion in Materials, DIMAT 96, ed. H.Mehrer, Chr. Herzig, N.A. Stolwijk, H. Bracht, Scitec Publications,
- H. Mehrer; N.A. Stolwijk (2009). "Heroes and Highlights in the History of Diffusion"
- S. Chapman, T. G. Cowling (1970) The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases, Cambridge University Press
- J.F. Kincaid; H. Eyring; A.E. Stearn (1941). "The theory of absolute reaction rates and its application to viscosity and diffusion in the liquid State". Chem. Rev
- A.N. Gorban, H.P. Sargsyan and H.A. Wahab (2011). "Quasichemical Models of Multicomponent Nonlinear Diffusion". Mathematical Modelling of Natural Phenomena.
- Onsager, L. (1931). "Reciprocal Relations in Irreversible Processes. I". Physical Review
- L.D. Landau, E.M. Lifshitz (1980). Statistical Physics.
- S. Bromberg, K.A. Dill (2002), Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology
- T. Teorell (1935). "Studies on the "Diffusion Effect" upon Ionic Distribution. Some Theoretical Considerations". Proceedings of the National Academy of Sciences of the United States of America
- Bian, Xin; Kim, Changho; Karniadakis, George Em (2016-08-14). "111 years of Brownian motion". Soft Matter.
- J. L. Vázquez (2006), The Porous Medium Equation. Mathematical Theory, Oxford Univ. Press,
- Stauffer, Philip H.; Vrugt, Jasper A.; Turin, H. Jake; Gable, Carl W.; Soll, Wendy E. (2009). "Untangling Diffusion from Advection in Unsaturated Porous Media: Experimental Data, Modeling, and Parameter Uncertainty". Vadose Zone Journal.
- S. H. Lam (2006). "Multicomponent diffusion revisited" (PDF). Physics of Fluids.
- Pasternack, Gregory B.; Brush, Grace S.; Hilgartner, William B. (2001-04-01). "Impact of historic land-use change on sediment delivery to a Chesapeake Bay subestuarine delta
- Gregory B. Pasternack. "Watershed Hydrology, Geomorphology, and Ecohydraulics :: TFD Modeling". pasternack.ucdavis.edu. Retrieved
- Mosby’s Dictionary of Medicine, Nursing, & Health Professions. 7th ed. St. Louis
- Weiss, G. (1994). Aspects and Applications of the Random walk


























![{\displaystyle \displaystyle {\frac {\partial n_{i}}{\partial t}}=-\operatorname {div} \mathbf {J} _{i}=-\sum _{j\geq 0}L_{ij}\operatorname {div} X_{j}=\sum _{k\geq 0}\left[-\sum _{j\geq 0}L_{ij}\left.{\frac {\partial ^{2}s(n)}{\partial n_{j}\,\partial n_{k}}}\right|_{n=n^{*}}\right]\,\Delta n_{k}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3edb55525efc68a86a6b624f7ce03f2023e6329)




















![{\displaystyle \displaystyle {\frac {\partial (n/n^{\ominus })}{\partial t}}=\nabla \cdot [{\mathfrak {m}}a(\nabla \mu -({\text{external force per mole}}))].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d7bc56bbf36ce8ac065ecc440037bf0ae349994)















![{\displaystyle {\displaystyle \mathbf {J} _{i}=-D_{i}[z\,\nabla c_{i}-c_{i}\nabla z]\,.}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd0f444df91bb40ecf9f2b645be1a99c20f5f75c)
![{\displaystyle {\displaystyle {\frac {\partial c_{i}}{\partial t}}=-\operatorname {div} \mathbf {J} _{i}=D_{i}[z\,\Delta c_{i}-c_{i}\,\Delta z]\,.}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2051eb510183445e2e49846f322e593bfabb1034)


![{\displaystyle {\displaystyle \mathbf {J} _{i}=-\sum _{j}D_{ij}[c_{j}\,\nabla c_{i}c_{i}\,\nabla c_{j}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/555f70c26c0bb507cc5408870ee7323418889b09)
![{\displaystyle {\displaystyle {\frac {\partial c_{i}}{\partial t}}=\sum _{j}D_{ij}[c_{j}\,\Delta c_{i}-c_{i}\,\Delta c_{j}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b400209accc603c72030e8ace9f8637744f33ead)































![{\displaystyle {\displaystyle D_{12}={\frac {3}{2n(d_{1}+d_{2})^{2}}}\left[{\frac {kT(m_{1}+m_{2})}{2\pi m_{1}m_{2}}}\right]^{1/2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88aaf3e042e6fb8b83e68845fdd1109f144369fc)
![{\displaystyle {\displaystyle D_{12}={\frac {3}{8nA_{1}({\nu })\Gamma (3-{\frac {2}{\nu -1}})}}\left[{\frac {kT(m_{1}+m_{2})}{2\pi m_{1}m_{2}}}\right]^{1/2}\left({\frac {2kT}{\kappa _{12}}}\right)^{\frac {2}{\nu -1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d0a141967a94aad8862fab3828f3c7003afe9a9)





















