مرتبسازی تیم
| رده | الگوریتم مرتبسازی |
|---|---|
| ساختمان داده | آرایه |
| کارایی بدترین حالت | [۱] |
| کارایی بهترین حالت | |
| کارایی متوسط | |
| پیچیدگی فضایی |
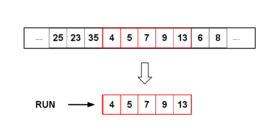
الگوریتم مرتبسازی تیم (به انگلیسی: Timsort)، ترکیبی از دو الگوریتم مرتبسازی است به نامهای مرتبسازی ادغامی و مرتبسازی درجی. این طراحی بر روی بسیاری از انواع دادهها در جهان واقعی بسیار خوب عمل میکند. این الگوریتم اولین بار توسط تیم پیترز (به انگلیسی: Tim Peters) در سال ۲۰۰۲ برای استفاده در پایتون بیان شد. الگوریتم برای پیدا کردن زیر مجموعهای از دادهها که جستجو را بهینهتر کنند، طراحی شد. بهوسیلهٔ مرتبسازی ادغامی زیر مجموعه مشخص میشود. این زیر مجموعه یک run نامیده میشود. از این runها به تعدادی پیدا میشود که معیارهای لازم برآورده شود. مرتبسازی تیم، مرتبسازی استاندارد پایتون از مدل ۲٫۳ است. هماکنون در جاوا ۷ و همچنین در اندروید برای مرتبسازی آرایهها از این مرتبسازی استفاده میشود.[۲]
الگوریتم چگونه کار میکند؟[ویرایش]
الگوریتم برای استفاده از این مزیت که دادهها بهطور جزئی مرتب شدهاند، طراحی شدهاست. جستجوی تیم، کار خود را با پیداکردن runها در داده ادامه میدهد. یک run یک زیرآرایه از آرایهٔ اصلی دادهها میباشد که حداقل دارای دو عنصر میباشد که غیر نزولی یا نزولی اکید باشد. اگر زیر مجموعه نزولی باشد باید نزولی اکید باشد زیرا این run میتواند با جابجایی ساده عناصر از دو طرف که به وسط همگرا میشوند، معکوس شود.
این الگوریتم اگر عناصر آن اکیداً نزولی باشد پایدار است. بعد از به دست آوردن یک run در آرایهٔ داده شده، عملیات خود را روی آن انجام میدهد و بعد از آن کار خود را با run بعدی ادامه میدهد.
یک run بهطور طبیعی یک زیرآرایه است که مرتب شدهاست. runهای طبیعی در دادههای واقعی میتوانند در اندازههای مختلفی وجود داشته باشند. این الگوریتم به صورت بهینه نوع خاصی از مرتبسازی که به طول run بستگی دارد (بهطور مثال اگر اندازهٔ آن از مقدار خاصی کمتر باشد از مرتبسازی درجی استفاده میکند) بنابراین این مرنبسازی انطباقی نامیده میشود.[۳] اندازهٔ run با اندازهٔ کوچکترین run مقایسه میشود. اندازهٔ کوچکترین run که «minrun» نامیده میشود که به اندازهٔ آرایه بستگی دارد. برای آرایههایی که اندازهٔ آن از ۶۴ کمتر باشد، اندازهٔ minrun به اندازهٔ خود آرایه میباشد و اساساً به مرتبسازی درجی تبدیل میگردد. برای آرایههای بزرگتر اندازهٔ minrun بین بازهٔ ۳۲ تا ۶۵ انتخاب میشود. الگوریتم نهایی برای انتخاب minrun، شش بیت قابل توجه اندازهٔ آرایه را در نظر میگیرد. اگر هر کدام از بیتهای باقیمانده یک بودند، یک اضافه میکند و از آن بهعنوان minrun استفاده میکند. این روش برای همهٔ آرایههایی که سایز آنها از ۶۴ کمتر است و شامل یک هستند، درست عمل میکند.[۳]
مرتبسازی درجی[ویرایش]
هنگامی که یک آرایه به صورت رندم باشد، با احتمال زیادی یک run طبیعی تعداد عناصر کمتری از minrun دارد. در این موارد تعداد مناسبی از عناصر در نظر گرفته میشوند و از مرتبسازی درجی برای مرتب کردن آنها استفاده میشود. سپس اندازهٔ آن افزایش مییابد تا به اندازهٔ minrun بشود.
مرتبسازی ادغامی[ویرایش]

عملیات ادغام معمولاً روی دو run پیاپی انجام میشود. برای این کار سه run بالای پشته را که مرتب نشدهاند را در نظر میگیرد. اگر طول این سه run را x، y، z در نظر بگیریم، الگوریتم طوری آنها را ادغام میکند که دو شرط زیر برقرار شود.
- X > Y + Z
- Y > Z
این دو قانون باعث میشود که طول runها نزدیک به هم نگه داشته شوند و بازدهی الگوریتم بالاتر باشد.
رویهٔ ادغامکردن[ویرایش]
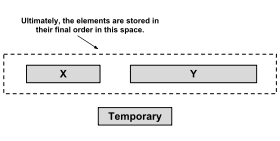
ادغام کردن دو run همسایه به کمک یک حافظهٔ کمکی انجام میشود. اندازهٔ این حافظه به اندازهٔ run کوچکتر میباشد. الگوریتم آرایهٔ کوچکتر را در حافظه کپی میکند و سپس برای ذخیرهٔ run نهایی از حافظهٔ اصلی و حافظهٔ run بزرگتر استفاده میکند.
کارایی الگوریتم[ویرایش]
طبق نظریه اطلاعات هیچ الگوریتم مرتبسازی مقایسهای نمیتواند کارایی بهتر از در حالت میانگین داشته باشد. در دادههای واقعی الگوریتم تیم معمولاً با تعداد مقایسههای کمتر از مرتبسازی را انجام میدهد زیرا از این مزیت که زیر مجموعهای از دادهها مرتب هستند.[۴] در مواردی که هیچ زیر مجموعهای از دادهها مرتبشده نیستند الگوریتم نمیتواند از این مزیت استفاده کند و با کارایی کار میکند.[۳] در جدول زیر کارایی الگوریتم با دیگر الگوریتمهای مقایسهای مقایسه شدهاست.
| مرتبسازی تیم | مرتبسازی ادغامی | مرتبسازی سریع | مرتبسازی درجی | مرتبسازی انتخابی | |
|---|---|---|---|---|---|
| بهترین حالت | |||||
| حالت متوسط | |||||
| بدترین حالت |
در جدول زیر انواع مختلف الگوریتمها بر اساس پیچیدگی مقایسه شدهاند.
| مرتبسازی تیم | مرتبسازی ادغامی | مرتبسازی سریع | مرتبسازی درجی | مرتبسازی انتخابی | |
|---|---|---|---|---|---|
| پیچیدگی حافظه | n | n | log n | 1 | 1 |
منابع[ویرایش]
- ↑ Peters, Tim. "[Python-Dev] Sorting". Python Developers Mailinglist. Retrieved 24 Feb 2011.
[Timsort] also has good aspects: It's stable (items that compare equal retain their relative order, so, e.g. , if you sort first on zip code, and a second time on name, people with the same name still appear in order of increasing zip code; this is important in apps that, e.g. , refine the results of queries based on user input). … It has no bad cases (O(N log N) is worst case; N-1 compares is best).
- ↑ Peters, Tim. "[Python-Dev] Sorting". Python Developers Mailinglist. Retrieved 24 Feb 2011.
[Timsort] also has good aspects: It's stable (items that compare equal retain their relative order, so, e.g. , if you sort first on zip code, and a second time on name, people with the same name still appear in order of increasing zip code; this is important in apps that, e.g. , refine the results of queries based on user input). … It has no bad cases (O(N log N) is worst case; N-1 compares is best).
- ↑ ۳٫۰ ۳٫۱ ۳٫۲ timsort, python. "python_timsort".
- ↑ Martelli, Alex (2006). Python in a Nutshell (In a Nutshell (O'Reilly)). O'Reilly Media, Inc. p. 57. ISBN 0-596-10046-9.











