الگوریتم حریصانه

روش حریصانه یا الگوریتم حریصانه (به انگلیسی: Greedy algorithm) یکی از روش‌های مشهور و پرکاربرد طراحی الگوریتم‌ها است که با ساختاری ساده در حل بسیاری از مسائل استفاده می‌شود. این روش اغلب در حل مسائل بهینه‌سازی به کار می‌رود و در پاره‌ای مواقع جایگزین مناسبی برای روش‌هایی مانند برنامه‌ریزی پویا است. در حالت کلی این روش سرعت و مرتبهٔ اجرایی بهتری نسبت به روش‌های مشابه خود دارد؛ اما متناسب با مسئله ممکن است به یک جواب بهینهٔ سراسری ختم نشود. این دسته از الگوریتم‌ها در علوم رایانه کاربرد وسیعی دارند.

در روش حریصانه رسیدن به هدف در هر گام مستقل از گام قبلی و بعدی است؛ یعنی در هر مرحله برای رسیدن به هدف نهایی، مستقل از این که در مراحل قبلی چه انتخاب‌هایی صورت گرفته و انتخاب فعلی ممکن است چه انتخاب‌هایی در پی داشته باشد، انتخابی صورت می‌پذیرد که در ظاهر بهترین انتخاب ممکن است. به همین دلیل است که به این روش، روش حریصانه گفته می‌شود. به‌طور مثال، زمانی که یک دزد عجول و حریص وارد خانه‌ای می‌شود، در مسیر حرکت خود هر وسیله و کالای با ارزشی را داخل کیسه می‌اندازد. وی در این حالت چندان توجهی نمی‌کند که چه اشیایی را قبلاً برداشته و ممکن است در آینده چه اشیاء گران‌بهاتری به دست آورد. او در هر گام تنها از بین اشیای دم‌دست خود باارزش‌ترین آن را انتخاب کرده و به وسایل قبلی اضافه می‌کند.

این روش کاربردهای عمومی نیز دارد. به‌طور مثال زمانی که در مقابل خرید از یک فروشگاه یک اسکناس تحویل فروشنده داده می‌شود، وی با یک حساب سرانگشتی سعی می‌کند با حداقل اسکناس‌ها و سکه‌های ممکن باقیماندهٔ پول را تولید کرده و به خریدار تحویل دهد. این حساب سرانگشتی ممکن است روش حریصانه باشد.

در بسیاری از موارد مسئله به‌طور مستقیم یا غیرمستقیم از ما می‌خواهند که یک متغیر را کمینه یا بیشینه کنیم. در اکثر مسائل این‌چنینی ما باید تعدادی انتخاب انجام دهیم و مسئله در تعدادی مرحله حل شود. بازهٔ وسیعی از این مسائل توسط الگوریتم‌های حریصانه قابل حل هستند.^[۱]

تاریخچه

نام این روش از شخصیت معروف اسکروج در داستان سرود کریسمس گرفته شده‌است. یکی از تفریحات و انگیزه‌های اسکروج، به دست آوردن پول بیشتر بود؛^[۲] الگوریتم حریصانه (Greedy) نیز مانند شیوه اسکروج می‌باشد؛ مثلاً فرض کنید اسکروج در یک مسابقه شرکت کرده‌است و باید در مرحلهٔ اول مسابقه یک در را انتخاب کند، به ازای انتخاب هر در فقط می‌تواند درهای بعد آن را باز کند و پول دریافت کند:

در مرحله اول باید بین دو در، اولی پنج سکه و دومی دو سکه، انتخاب کند؛ چون او حریص است بهترین انتخاب را در لحظه انتخاب در اول می‌داند.

در مرحله دوم در بعد از در اول دارای سه سکه است و او با هشت سکه خارج می‌شود؛ حال در بعد از در دوم را بررسی می‌کنیم؛ ممکن است دارای یک سکه باشد که در این صورت انتخاب حریصانه اسکروج بهینه بوده‌است یا ممکن است ده سکه باشد که در این صورت نشان می‌دهد که انتخاب بهینه در هر مرحله لزوماً منجر به سود بیشینه نمی‌شود. [۱]

ساختار روش حریصانه

کلیت روش حریصانه در هر مرحله، انتخاب یک عنصر از عناصر موجود است. کار با یک مجموعه تهی شروع شده و این عنصر قسمتی از جواب مسئله است که به ترتیبی خاص به مجموعه عناصر نهایی اضافه می‌شود.

به دلیل این که هر الگوریتم حریصانه الزاماً حل بهینه را نمی‌دهد، برای هر مسئلهٔ خاص باید اثبات کنیم که آیا الگوریتم حریصانه برای آن، جواب بهینه می‌دهد یا خیر و این موضوع اغلب سخت‌ترین مرحله کار است.

در طی این مسیر گام‌های زیر اتفاق می‌افتد:

روال انتخاب حریصانه (Selection): در این گام یک عنصر برای اضافه شدن به مجموعه جواب انتخاب می‌شود. معیار یا روال انتخاب عنصر برای اضافه شدن، ارزش آن عنصر است. بسته به نوع مسئله، هر عنصر ارزشی دارد که باارزش‌ترین آن‌ها انتخاب می‌شود.
امکان‌سنجی و افزودن (Feasible): پس از انتخاب یک عنصر به‌صورت حریصانه، باید بررسی شود که آیا امکان اضافه کردن آن به مجموعه جواب‌های قبلی وجود دارد یا نه. گاهی اضافه شدن عنصر یکی از شرایط اولیهٔ مسئله را نقض می‌کند که باید به آن توجه نمود. اگر اضافه کردن این عنصر هیچ شرطی را نقض نکند، عنصر اضافه خواهد شد؛ وگرنه کنار گذاشته می‌شود و بر اساس گام اول عنصر دیگری برای اضافه شدن انتخاب می‌شود. اگر گزینهٔ دیگری برای انتخاب وجود نداشته باشد، اجرای الگوریتم به اتمام می‌رسد.
بررسی اتمام الگوریتم (Solution): در هر مرحله پس از اتمام گام دوم و اضافه شدن یک عنصر جدید به مجموعه جواب، باید بررسی کنیم که آیا به یک جواب مطلوب رسیده‌ایم یا خیر؟ اگر نرسیده باشیم به گام اول می‌رویم و چرخه را در مراحل بعدی ادامه می‌دهیم.

به زبان ساده، در روش حریصانه طی هر مرحله یک عنصر به روش حریصانه به مجموعه جواب اضافه شده، شرط محدودیت‌ها بررسی شده و در صورت نبود مشکل، عنصر و عناصر بعدی به همین ترتیب به مجموعه جواب اضافه می‌شوند. در طی این گام‌ها اگر به یک شرط نهایی خاص برسیم، یا امکان انتخاب عنصر دیگری برای اضافه کردن به مجموعه جواب وجود نداشته باشد، الگوریتم پایان می‌یابد و مجموعه جواب به‌دست‌آمده به‌عنوان جواب بهینه ارائه می‌شود. توجه داشته باشید که ممکن است بر اساس نوع مسئله، ترتیب اضافه شدن عناصر به مجموعه جواب اهمیت داشته باشد.^[۳]

 set_greedy(C){
    S = ∅;
    while(!solution(s) && C != ∅){
        X = select(C);
        C = C - {x};
        if (feasible(S,{x})){
            S = S + {x};
        }
    }
    if(solution(S)){
        return S;
    }
    else
        return ∅;
  }

روش اثبات درستی

هرچند روش یکتایی برای اثبات درستی الگوریتم حریصانه وجود ندارد ولی روش زیر در خیلی از مواقع الگوریتم را اثبات می‌کند. روش اثبات به این صورت است که دنبالهٔ تصمیمات اتخاذ شده در هر مرحله را در نظر گرفته، دنباله‌ای بهینه پیدا می‌کنیم که با دنبالهٔ ساخته شده یکسان باشد (منظور از دنبالهٔ بهینه، دنباله‌ای از کارها می‌باشد که جواب بهینه را به ما می‌دهد). برای پیدا کردن دنباله، ابتدا یک دنباله بهینه را درنظر می‌گیریم و در هر مرحله یک دنباله شبیه‌تر به دنباله خودمان پیدا می‌کنیم که بهینه باشد و سرانجام دنباله‌ای که پیدا کردیم با دنبالهٔ ما یکسان می‌شود.

میزان شباهت دنباله ${\mathit {E}}=e_{1},e_{2},...,e_{3}$ و ${\mathit {F}}=f_{1},f_{2},...,f_{3}$ را بزرگ‌ترین اندیسی مثل ${\mathit {x}}$ در نظر می‌گیریم که $\forall _{{\mathit {y}}<{\mathit {x}}}:e_{y}=f_{y}$

درواقع شباهت دو دنباله، بزرگ‌ترین عددی مثل ${\mathit {x}}$ است که ${\mathit {x}}$ عضو اول ابتدای هر دو دنباله با هم یکسان باشد.[۲]

محدودیت‌های الگوریتم حریصانه

جستجوی حریصانه — پیدا کردن بزرگ‌ترین مسیر در گراف وزن‌دار با استفاده از روش حریصانه

چون روش این الگوریتم گرفتن بهترین تصمیم در هر مرحله است، در بسیاری از موارد به راه‌حل بهینه سراسری ختم نمی‌شود. عمده مسائلی که این الگوریتم به جواب درست منتهی نمی‌شود، مسائل مربوط به گراف‌های وزن‌دار است؛ مثل مسئله فروشنده دوره‌گرد یا پیدا کردن بزرگ‌ترین مسیر در گراف وزن‌دار.^[۴]

تفاوت‌های الگوریتم حریصانه و برنامه‌نویسی پویا

الگوریتم حریصانه در هر مرحله بهترین جواب محلی را پیدا می‌کند؛ اما در برنامه‌نویسی پویا مسئله به تعدادی زیرمسئله تقسیم می‌شود.
الگوریتم حریصانه هیچ‌گاه در جواب خود بازنگری نمی‌کند.
در الگوریتم حریصانه تضمینی برای جواب نهایی بهینه وجود ندارد.
این الگوریتم در زمان بهینه اجرا می‌شود.^[۵]

کاربردها

مسئلهٔ کوله‌پشتی

ما n شی و یک کوله‌پشتی داریم که هر شیء دارای وزنی است؛ ظرفیت کوله‌پشتی نیز محدود است. ما می‌خواهیم ارزش شی‌ءهای قرار داده شده در کوله‌پشتی بیشینه شود: ما به دنبال $\sum _{k=1}^{N}p_{i}x_{i}$ Max هستیم، طوری که $\sum _{i=1}^{n}w_{i}x_{i}$ کمتر از W (بیشترین وزنی که در کوله‌پشتی قرار می‌گیرد. حال با توجه به روش حریصانه، راه حل‌های زیر موجودند:

هدف پیدا کردن بیشترین ارزش است، بنابراین اشیا را بر اساس سود آن‌ها به ترتیب نزولی مرتب کرده و اشیا با بیشترین ارزش را تا زمانی که کوله‌پشتی ظرفیت داشته باشد انتخاب می‌کنیم.
وزن اشیا تأثیر منفی دارد؛ یعنی انتخاب شی با وزن بیشتر به سرعت کوله‌پشتی را پر می‌کند؛ بنابراین اشیا را به ترتیب صعودی بر اساس وزن در نظر گرفته و هنگامی که ظرفیت کوله‌پشتی به حداکثر نرسیده‌است، اشیا با وزن کمتر را انتخاب می‌کنیم.
ارزش اشیا تأثیر مثبت و وزن آن‌ها تأثیر منفی دارد، بنابراین بهتر است نسبت p_i / x_i را محاسبه و به ترتیب نزولی مرتب کنیم، تا زمانی ظرفیت کوله‌پشتی به حداکثر نرسیده‌است، اشیا را از این لیست را انتخاب کنیم.

جواب‌های حاصل از مورد ۱ و ۲ لزوماً بهینه نیستند اما جواب حاصل از روش سوم بهینه است.^[۶]

حل یک مسئله با روش اول

مسئله: خریداری از یک فروشگاه یک جنس ۶۴ تومانی می‌خرد و ۱۰۰ تومان به فروشنده می‌دهد و فروشنده باید ۳۶ تومان به او بازگرداند. اگر فروشنده سکه‌های ۵۰ ,۲۵ ,۱۰ ,۵ ,۱ تومانی (از هر کدام حداقل یک نمونه) داشته باشد، چگونه می‌توان بقیه پول خریدار را برگرداند به نحوی که تعداد سکه‌ها (در کل) کمترین مقدار ممکن باشد؟

پاسخ: فرض کنید می‌خواهیم n تومان را با سکه‌های ۲۵ تومانی، ۱۰ تومانی، ۵ تومانی و ۱ تومانی پرداخت کنیم؛ به‌طوری که کمترین تعداد سکه را بپردازیم. ما می‌توانیم یک الگوریتم حریصانه برای حل این مسئله ارائه دهیم که تعداد سکه بهینه را در هر مرحله به دست آورد. برای این کار ما در هر مرحله بزرگ‌ترین سکه‌ای را که از پول باقی‌مانده تجاوز نکند انتخاب می‌کنیم در این صورت تعداد سکه‌ها بهینه خواهد بود.

در ابتدا هیچ سکه‌ای در مجموعه جواب نداریم. از بین سکه‌های موجود بزرگ‌ترین ممکن یعنی ۲۵ تومانی را انتخاب می‌کنیم. این مرحله از الگوریتم حریصانه را روال انتخاب (select procedure) گویند. اگر یک سکه ۲۵ تومانی دیگر را انتخاب کنیم حاصل از ۳۶ تومان بیشتر شده، لذا آن را کنار گذاشته به سراغ سکهٔ ۱۰ تومانی می‌رویم. حال بررسی می‌کنیم اگر این سکهٔ ۱۰ تومانی را به مجموعهٔ انتخابی قبلی اضافه کنیم، حاصل از ۳۶ تومان بیشتر می‌شود یا خیر. این مرحله را تحقیق عملی بودن (feasibility check) می‌نامند. حال اگر این ۱۰ تومان را به ۲۵ تومان اضافه کنیم، جمع مجموعهٔ انتخاب‌شده ۳۵ می‌شود که هنوز به ۳۶ نرسیده‌است. این مرحله را تحقیق حل شدن (Solution check) می‌گوییم. در ادامه سکه‌های دیگر را به ترتیب مقایسه می‌کنیم و در نهایت با انتخاب سکه یک تومانی در کل با ۳ سکه (۲۵ تومانی و ۱۰ تومانی و یک تومانی) ۳۶ تومان به دست می‌آید و این حداقل تعداد سکه ممکن است.

توجه کنید در انتخاب فوق، ملاک انتخاب، برای انتخاب بهترین سکه در هر مرحله (بهینهٔ محلی) سکه است و در انتخاب سکه در هر مرحله به انتخاب‌های قبلی و بعدی کاری نداریم. در این شیوه اجازهٔ فکر کردن دربارهٔ یک انتخاب انجام شده را نداریم؛ یعنی هنگامی که سکه‌ای پذیرفته شد به‌طور دائم جزو حل به حساب می‌آید و هنگامی هم که سکه‌ای رد می‌شود به‌طور دائم از حل کنار گذاشته می‌شود.^[۷]

کد مربوط به روش اول:

procedure change ({c_1}, {c_2}, {...}, {c_r}: value of denominations of coin, where {c_1}> {c_2}> {...}> {c_r}; n : a positive integer) {
    for i := 1 to r {
        while n>= {c_i} {
            // add a coin with value {c_i} to change
            n := n - {c_i}
        }
    }
}

همان‌طور که مشاهده کردید این روش بسیار ساده است، ولی اصلی‌ترین نکته این است که آیا این روش الزاماً به یک حل بهینه می‌رسد؟ در رابطه با مسئلهٔ خاص فوق می‌توان اثبات کرد که جواب بهینه است ولی با مثال زیر نشان می‌دهیم که ممکن است این گونه نباشد.

فرض کنید قرار است به فردی ۱۶ تومان پس بدهیم. سکه‌های موجود ۵۰ ,۲۵ ,۱۰ ,۵ ,۱ تومانی است (با این که ما در ایران سکهٔ ۱۲ تومانی نداریم ولی این فرض را بکنید که داریم).

با الگوریتم حریصانهٔ فوق به این نتیجه می‌رسیم که باید به این فرد یک سکه ۱۲ تومانی و ۴ سکه ۱ تومانی بدهیم؛ یعنی جمعاً ۵ سکه. در حالی که حل بهینهٔ مسئلهٔ فوق یک سکهٔ ۱۰ تومانی، یک سکهٔ ۵ تومانی و یک سکهٔ یک تومانی است؛ یعنی در کل ۳ سکه.

حل یک مسئله با روش سوم

مسئله (کوله‌پشتی صفر و یک): مثالی از این مسئله مربوط به دزدی می‌شود که با کوله‌پشتی وارد یک جواهر فروشی می‌شود. اگر وزن قطعات از یک حد بیشینه W فراتر رود، کوله‌پشتی پاره خواهد شد. هر قطعه دارای ارزش و وزن معینی خواهد بود. مسئله‌ای که دزد با آن مواجه است، تعیین حداکثر ارزش قطعات است در حالی که وزن کل آن‌ها از حد معین W فراتر نرود. این مسئله را کوله‌پشتی صفر و یک می‌گویند.

پاسخ: فرض کنید n قطعه وجود داشته باشد، به طوری که:

[s = [item1, item2, item3, ..., itemn

وزن Wi = item1

ارزش Pi = itemi

W = حداکثر وزنی که کوله پشتی قادر به تحمل آن است.

و wi ,pi ,w همگی اعداد صحیح هستند. راه حل جستجوی جامع این است که همهٔ زیرمجموعه‌های این n قطعه را در نظر بگیریم، زیرمجموعه‌هایی را که وزن کل آن‌ها از w فراتر نرود، کنار می‌گذاریم و از میان آن‌هایی که باقی می‌ماند، آن را که بیشترین ارزش را دارد، انتخاب می‌کنیم.^[۸]

void greedy_knap_sack(w, n){
    sort(p, w);
    for(i = 0; i <n; i++){
        x[i] = 0;
    }
    u = w
    for(i = 0; i <n; i++){
        if(w[i]> u)
            break;
        x[i] = 1;
        u = u - w[i];
    }
    if (i <n) {
        x[i] = u / w[i];
    }
}

مسئلهٔ رنگ‌آمیزی رأس‌های گراف:

با تعداد m رنگ داده شده، رأسهای گراف باید به گونه‌ای رنگ شوند که هیچ دو رأس مجاوری دارای رنگ مشابه نباشند. هدف رنگ کردن رأس‌ها به شیوه‌ای است که هیچ دو رأس مجاوری دارای رنگ مشابه نباشند. هیچ الگوریتم کارآمدی برای رنگ‌آمیزی گراف با حداقل رنگ‌های ممکن وجود ندارد و این مسئله از جمله مسائل «ان‌پی کامل» (NP Complete) محسوب می‌شود. «الگوریتم‌های تقریبی» (Approximate Algorithms) گوناگونی برای حل این مسئله وجود دارند، که رنگ‌آمیزی حریصانه از جمله آنهاست. رنگ‌آمیزی حریصانه به این صورت است که رأس اول را با رنگ اول رنگ می‌کنیم و همه رأس‌های بعدی را با اولین رنگی که در رأس‌های مجاور آن وجود نداشت رنگ می‌کنیم. اگر چنین رنگی وجود نداشت، رنگ جدیدی اضافه می‌کنیم.^[۹]

void greedyColoring(std::vector<V>)
{

int result[V.size()];
result[0] = 0;
for (int u = 1; u <V.size(); u++)
result[u] = -1;
bool available[V.size()];
for (int cr = 0; cr <V.size(); cr++)
available[cr] = false;
for (int u = 1; u <V.size(); u++)
{
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
if (result[*i] != -1)
available[result[*i]] = true;
int cr;
for (cr = 0; cr <V.size(); cr++)
if (available[cr] == false)
break;
result[u] = cr;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
if (result[*i] != -1)
available[result[*i]] = false;
}
  }

مسئلهٔ برنامه‌ریزی چندین فعالیت همزمان:

مسئلهٔ برنامه‌ریزی چندین فعالیت که همزمان انجام می‌پذیرند نیاز به استفادهٔ همزمان از یک منبع مشترک با هدف انتخاب مجموعه‌ای با ماکزیمم اندازه از فعالیت‌هایی که با هم هم‌پوشانی ندارند، دارند.

فرض کنید یک مجموعهٔ {s = {a1, a2, …, an از n فعالیت پیشنهادی داریم که می‌خواهند از یک منبع استفاده نمایند، مانند یک تالار سخنرانی که در یک زمان می‌تواند تنها مورد استفادهٔ یک فعالیت قرار گیرد. هر فعالیت ai دارای زمان شروع si و زمان خاتمهٔ fi است به‌طوری‌که ۰ ≤ fi> si <∞. اگر فعالیت ai انتخاب شود، می‌تواند در طول بازهٔ (si, fi] رخ دهد.

تعریف: دو فعالیتی را سازگار می‌گوییم که با یکدیگر هم‌پوشانی نداشته باشند.

مسئله انتخاب فعالیت عبارت است از انتخاب یک زیرمجموعه با ماکزیمم اندازه از فعالیت‌هایی که هم‌پوشانی ندارند. برای مثال زیرمجموعهٔ s از فعالیت‌ها را در نظر بگیرید که آن‌ها را برحسب زمان پایان به ترتیب صعودی یکنواخت مرتب کرده‌ایم:

  i -> 1 2 3 4 5 6 7 8 9 10 11
  si -> 1 3 0 5 3 5 6 8 8 2 12
  fi -> 4 5 6 7 8 9 10 11 12 13 14

برای این مثال زیرمجموعهٔ {a3, a9, a11} شامل فعالیت‌هایی است که هم‌پوشانی ندارند.

اگرچه این زیرمجموعه بیشینه نیست، چون زیرمجموعهٔ {a1, a4, a9, a11} بزرگ‌تر از آن است. در حقیقت {a1, a4, a9, a11} بزرگ‌ترین زیرمجموعه از فعالیت‌های متقابلاً سازگار است.

حال یک الگوریتم حریصانه بازگشتی برای حل مسئلهٔ زمان‌بندی فعالیت‌ها ارائه خواهیم نمود.

با تعریف مجموعهٔ {sij = {ak € s: fi ≤ sk <fk ≤ sj شروع می‌کنیم، به‌طوری‌که sij زیرمجموعه‌ای از فعالیت‌ها در S است که می‌توانند بعد از خاتمه فعالیت ai شروع شده و قبل از شروع فعالیت aj خاتمه یابند. در حقیقت sij شامل همه فعالیت‌هایی است که با ai و aj و همچنین با همه فعالیت‌هایی که بعد از خاتمه ai خاتمه نیافته و همه فعالیت‌هایی که قبل از شروع aj شروع نمی‌شوند، سازگارند. به منظور بیان کل مسئله، فعالیت‌های ساختگی a0 و an+1 را اضافه کرده و توافق می‌کنیم که f0 = ۰ و ∞ = sn+1 پس s = s0, n+1 و محدودهٔ تغییر i و j به صورت زیر خواهد بود:

0 ≤ i, j ≤ n+1

دامنهٔ تغییر i و j را به صورت زیر می‌توانیم بیشتر محدود کنیم. فرض می‌کنیم که فعالیت‌ها در یک ترتیب یکنواخت صعودی از زمان‌های خاتمه مرتب شده‌اند:

f0 ≤ f1 ≤ f2 ≤ … ≤ fn ≤ fn+1 ادعا می‌کنیم که sij = ᴓ هر گاه i ≥ j باشد. فرض کنید یک فعالیت ak € sij برای i ≥ j وجود دارد به‌طوری‌که ai بعد از aj در ترتیب مرتب قرار دارد. پس خواهیم داشت fi ≤ sk <fk ≤ sj <fj. بنابراین fi <fj که با این فرض که ai بعد از aj در ترتیب مرتب قرار دارد در تناقض است. می‌توانیم نتیجه بگیریم با این فرض که فعالیت‌ها را در یک ترتیب صعودی یکنواخت از زمان‌های خاتمه مرتب کرده‌ایم، فضای زیر مسائل انتخاب زیر مجموعه با ماکزیمم اندازه شامل فعالیت‌های متقابلاً سازگاراز sij است، که با آگاهی از این مطلب که تمام sijهای دیگر تهی هستند رابطه زیر برقرار است:

0 ≤ i, j ≤ n+1

برای مشاهدهٔ زیرساختار مسئلهٔ انتخاب فعالیت، تعدادی زیرمسئله غیر تهی sij را در نظر بگیرید؛ و فرض کنید که یک جواب برای sij شامل تعدادی فعالیت ak است. به‌طوری‌که fi ≤ sk <fk ≤ sj. استفاده از فعالیت ak سبب ایجاد دو زیرمسئله می‌شود، sik (فعالیت‌هایی که پس از خاتمهٔ فعالیت ai شروع شده و قبل از شروع فعالیت ak خاتمه می‌یابند) و skj (فعالیت‌هایی که پس از خاتمهٔ ak شروع شده و قبل از شروع فعالیت aj خاتمه می‌یابند)، که هر کدام از یک زیرمجموعه شامل فعالیت‌های داخل sij تشکیل شده‌اند. جواب sij اجتماع جواب‌های مربوط به sik و skj است، همراه با فعالیت ak. بنابراین تعداد فعالیت‌ها در جواب sij برابر اندازه جواب skj به علاوه یک (برای ak) می‌باشد.

اکنون فرض کنید جواب Aij برای sij شامل فعالیت ak می‌باشد. پس جواب‌های Aik برای sik و Akj برای skj که در این جواب بهینه برای sij استفاده می‌شوند نیز باید بهینه باشند. بحث برش – و – الصاق معمول در این مورد بکار می‌رود. اگر یک جواب Áik برای sik می‌داشتیم که شامل فعالیت‌های بیشتری از Aik می‌بود، می‌توانستیم Aik را از داخل Aij برش داده و به داخل Áik الصاق نماییم، بنابراین یک جواب دیگر برای sij با تعداد فعالیت‌های بیشتری از Aij تولید می‌شود. از آنجا که فرض کردیم Aij یک جواب بهینه است، به یک تناقض رسیده‌ایم. به‌طور مشابه اگر جواب Ákj برای skj را با فعالیت‌های بیشتر از Akj می‌داشتیم، می‌توانستیم Akj را با Ákj جایگزین کنیم تا یک جواب با فعالیت‌های بیشتری از Aij تولید نماییم.

اکنون از زیرساختار بهینه خود استفاده می‌کنیم تا نشان دهیم که می‌توانیم یک جواب بهینه برای مسئله از روی جواب‌های بهینهٔ زیرمسائل بسازیم. مشاهده کردم که هر جواب برای یک زیرمسئلهٔ غیرتهی sij شامل فعالیت ak است و آن که هر جواب بهینه در درون خود شامل جواب‌های بهینهٔ نمونه زیرمسئله‌های sik و skj می‌باشد؛ بنابراین، می‌توانیم یک زیرمجموعه با ماکزیمم اندازه از فعالیت‌های متقابلاً سازگار در sij بسازیم. با تقسیم مسئله به دو زیرمسئله (یافتن زیرمجموعه‌های با ماکزیمم اندازه از فعالیت‌های متقابلاً سازگار در sik و skj) و پیدا کردن زیرمجموعه‌های با ماکزیمم اندازه Aik و Akj از فعالیت‌های متقابلاً سازگار برای این زیرمسائل و سپس تشکیل زیرمجموعه Aij با ماکزیمم اندازه شامل فعالیت‌های متقابلاً سازگار به صورت Aik υ {ak} υ Akj = Aij یک جواب بهینه برای کل مسئله و یک جواب برای s0, n+1 است.^[۱۰]

کسر مصری:

هر کسر مثبتی را می‌توان به صورت مجموع چند کسر واحد متفاوت نوشت. (کسر واحد به کسری گفته می‌شود که صورت آن یک و مخرجش یک عدد طبیعی است)

ورودی: صورت و مخرج کسری که می‌خواهیم به صورت مجموع چند کسر واحد بنویسیم.

خروجی: مخرج کسرهای واحدی که کسر ورودی را تولید می‌کنند.^[۱۱]

def egyptianFraction(nr, dr):
    print("The Egyptian Fraction " +
          "Representation of {0}/{1} is".
                format(nr, dr), end="\n")

    ef = []
    while nr != 0:
        x = math.ceil(dr / nr)
        ef.append(x)
        nr = x * nr - dr
        dr = dr * x
    return ef

تولید درخت پوشای کمینه:

روش‌های پریم و کروسکال دو روش مشهور تولید درخت پوشای کمینه از یک گراف وزن‌دار هستند که از روش حریصانه بهره می‌برند. منظور از درخت پوشای کمینه، درخت پوشایی از گراف است که مجموع وزن یال‌های آن کمتر یا مساوی مجموع وزن یال‌های سایر درخت‌های پوشای آن گراف است.^[۱۲]

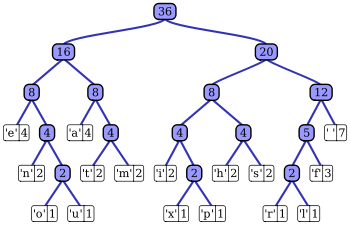
کدگذاری هافمن

کدگذاری هافمن یک الگوریتم مقایسهٔ داده است که از الگوریتم حریصانه برای پیاده‌سازی استفاده می‌کند و بر اساس تعداد تکرارهای یک کاراکتر در یک فایل است. این کدگذاری در فشرده‌سازی اطلاعات به کار می‌رود و با کدگذاری مجدد کاراکترهای موجود در اطلاعات بر اساس میزان استفادهٔ آن‌ها، سعی در کم کردن حجم فایل می‌کند. بر اساس این روش، کاراکتری با استفادهٔ بالا با کد کوتاهتر و کاراکتری با استفادهٔ کم با کد طولانی‌تر جایگزین می‌شود.^[۱۳]

الگوریتم دایسترا (دکسترا)

این الگوریتم در سال ۱۹۵۶ توسط ادسخر دکسترا (Edsger Dijkstra) اثبات شد؛ که جزو الگوریتم‌های جستجوی گراف است، و سؤالاتی چون کوتاه‌ترین مسیر از یک رأس در گراف‌های بدون وزن منفی را حل می‌کند. همچنین در مسیریابی (routing) و به عنوان یک زیرروال (subroutine) در الگوریتم‌های دیگر گراف استفاده می‌شود.^[۱۴]

def dijkstra(Adj, w, s):
  parent = [None] * len(Adj)  # Same
  parent[s] = s               # init
  d = [math.inf] * len(Adj)   # as
  d[s] = 0                    # before.

  Q = PriorityQueue.build(Item(id=u, key=d[u]) for u in Adj)

  while len(Q)> 0:
    u = Q.delete_min().id     # Delete and process u
    for v in Adj[u]:              # Same
      if d[v]> d[u] + w(u,v):    # relax
        d[v] = d[u] + w(u,v)      # as
        parent[v] = u             # before.
        Q.decrease_key(id=v, new_key=d[v]) # NEW!

  return d, parent

پانویس

↑ ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 258.
↑ Fred Guida، A Christmas Carol and Its Adaptations: A Critical Examination of Dickens's ...، 230.
↑ ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 258.
↑ «آموزش ساختمان داده و الگوریتم در برنامه‌نویسی». Quera College.
↑ A.A.Puntambekar، Advanced Data Structures and Algorithms، 11-2.
↑ Hari Mohan Pandey، Design Analysis and Algorithm، 289.
↑ ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 259,258.
↑ ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 287,288.
↑ K Erciyes، Guide to Graph Algorithms: Sequential, Parallel and Distributed، 362.
↑ Hari Mohan Pandey، Design Analysis and Algorithm، 293.
↑ Stan Wagon، Mathematica in Action، 322.
↑ ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 265.
↑ Richard E. Neapolitan, Kumarss Naimipour، Foundations of Algorithms Using Java Pseudocode، 169.
↑ Jesse Russell- Ronald Cohn، Dijkstra's Algorithm.

منابع

مقدمه‌ای بر الگوریتم‌ها - پدیدآورنده: تامس کورمن، چارلز لیزرسان، رونالد دیوست، کلیفورد اشتاین - (clrs)
درس و کنکور طراحی الگوریتم، مؤلف: حمیدرضا مقسمی،انتشارات گسترش علوم پایه
علایی فرادنبه - علایی، ابراهیم، محمدرضا (۱۳۹۲). طراحی الگوریتم. تهران: انتشارات راه.

Discrete Mathematics and its Applications, Kenneth H.Rosen, fifth edition

Greedy Algorithm Archives - GeeksforGeeks

Dijkstra's Algorithm,Jesse Russell, Ronald Cohn, Book on Demand, 2012
Advanced Data Structures and Algorithms, A.A.Puntambekar, Technical publication pune, 2008
Design Analysis and Algorithm, Hari Mohan Pandey, University science Press, 2008
Guide to Graph Algorithms: Sequential, Parallel and Distributed, K Erciyes, Springer, 2018
Foundations of Algorithms Using Java Pseudocode, Richard E. Neapolitan, Kumarss Naimipour, Jones andBartlett publishers , 2004
Mathematica in Action, Stan Wagon, Springer, 2000
A Christmas Carol and Its Adaptations: A Critical Examination of Dickens's … , Fred Guida, Mc Farland, 2000

پیوند به بیرون

www.old.roshd.ir

www.quera.ir/college

[1] ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 258.

[2] Fred Guida، A Christmas Carol and Its Adaptations: A Critical Examination of Dickens's ...، 230.

[3] ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 258.

[4] «آموزش ساختمان داده و الگوریتم در برنامه‌نویسی». Quera College.

[5] A.A.Puntambekar، Advanced Data Structures and Algorithms، 11-2.

[6] Hari Mohan Pandey، Design Analysis and Algorithm، 289.

[7] ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 259,258.

[8] ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 287,288.

[9] K Erciyes، Guide to Graph Algorithms: Sequential, Parallel and Distributed، 362.

[10] Hari Mohan Pandey، Design Analysis and Algorithm، 293.

[11] Stan Wagon، Mathematica in Action، 322.

[12] ابراهیم علایی فرادنبه - محمدرضا علایی، طراحی الگوریتم ایران، 265.

[13] Richard E. Neapolitan, Kumarss Naimipour، Foundations of Algorithms Using Java Pseudocode، 169.

[14] Jesse Russell- Ronald Cohn، Dijkstra's Algorithm.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]

[۸]

[۹]

[۱۰]

[۱۱]

[۱۲]

[۱۳]

[۱۴]